涂层锆合金包壳管切向微动磨损数值预测模型研究

王凯模，沈火明，王宇星，2，廖业宏，刘 娟，任啟森，彭振驯，黄 恒

（1.西南交通大学力学与航空航天学院，成都 610031；2.西南交通大学机械工程学院，成都 610031；3.中广核研究院有限公司核燃料与材料研究所，广东 深圳 518026）

0 引言

核燃料包壳作为核反应堆安全的首道屏障，能够防止核裂变产物的泄漏，其完整性是决定反应堆正常、高效运行的关键。而反应堆中冷却水自下而上的流动会导致核燃料包壳与其支撑格架之间发生严重的微动磨损［1］，引起核燃料组件的破坏及失效，严重时甚至会造成核裂变产物的泄漏。因此，研究包壳-格架的微动磨损行为对于保障核反应堆寿命是至关重要的。

研究人员对包壳微动磨损行为开展了大量研究工作。邓星［2］研究在球-平面接触下，交变载荷条件下Zr-4合金的切向微动磨损特性，发现磨损体积和磨损深度随着位移幅值增加而增加。赵杰江等［3］通过二维柱面-平面有限元模型模拟了锆合金切向微动磨损试验，结果表明在整体滑移状态下，锆合金磨损速率随位移幅值增加而增加，随法向力增加先增加后减小。在部分滑移状态下，磨损率随位移幅值的增加增长缓慢，随法向力增加缓慢减小。高雯［4］对包壳磨损的摩擦因数进行了研究，发现摩擦因数随载荷的增加呈线性增加趋势。Attia［5］研究了锆合金在高温下的微动磨损行为，发现锆合金的磨损率随功率的增加而减小。齐欢欢等［6］采用Archard模型［7］预测了燃料棒包壳与格架之间的微动磨损，发现磨损预测需要确定磨损系数、接触力和滑动距离3个参数。唐力晨等［8］建立了锆合金管-格架弹簧微动磨损的计算分析模型，发现磨损量和最大磨损深度随磨损周次的计算结果与试验结果符合较好。近年来，法国原子能协会、法玛通等机构对涂层锆合金的微动磨损行为进行了研究，研究均表明涂层锆合金能显著降低包壳的磨损程度［9－10］。综上所述，目前研究主要针对锆合金包壳的微动磨损，针对铬涂层锆合金包壳［11］的微动磨损研究较少，同时缺少对包壳-格架实际几何特征的考虑。

本研究考虑包壳-刚凸的几何特征，建立对应的有限元模型，基于Archard磨损计算模型在ABAQUS中结合ALE自适应功能实现磨损仿真。通过涂层锆合金管-刚凸切向微动磨损试验获得摩擦因数、磨损系数的试验数据，同时考虑磨损系数随磨损周次的变化情况，最后得到涂层锆合金管-刚凸切向微动磨损的有限元计算模型。本文中建立的模型可较好地预测涂层包壳管-刚凸的最大磨损深度，对包壳-格架系统的磨损预测具有参考意义。

1 有限元模型

为研究包壳管-刚凸的切向磨损行为，根据包壳管和刚凸的几何尺寸，同时参照切向磨损试验中包壳管-刚凸的约束形式，建立如图1所示的包壳-刚凸三维有限元模型。截面尺寸如图2所示，刚凸沿Z方向宽度为3.3 mm，包壳管沿Z方向宽度取6 mm。

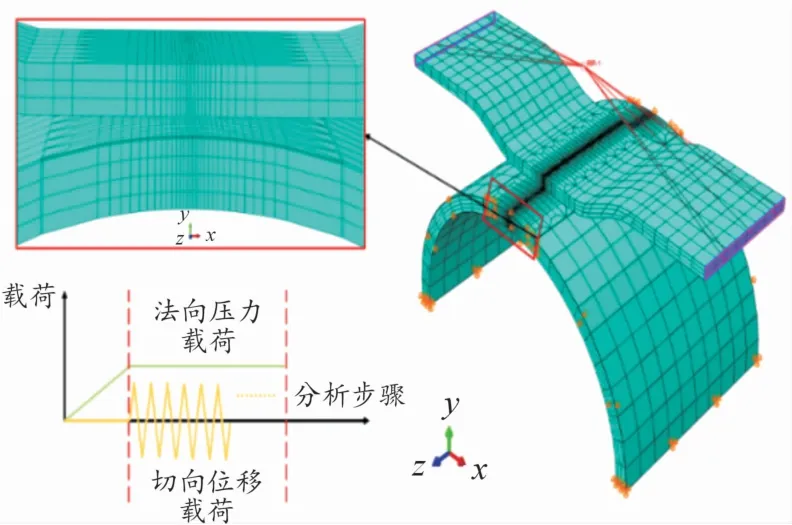
图1 包壳-刚凸有限元模型／加载方式

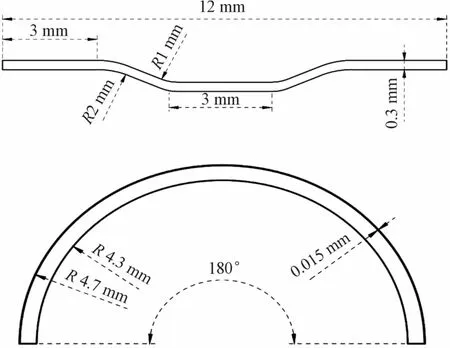
图2 截面尺寸示意图

同时考虑模型计算效率和计算精度，对模型接触区域进行局部网格加密，刚凸的最小网格尺寸为16μm×75μm×173.5μm，包壳管的最小网格尺寸为13μm×5μm×200μm，单元类型为C3D8R。接触设置为面-面接触，包壳管表面设置为主面，刚凸表面设置为从面，切向设置为具有各向同性摩擦的库仑摩擦定律，摩擦因数为0.6；法向设置为硬接触，采用有限滑移算法，切向约束设置为“罚”。

包壳轴向截面采用铰接约束，周向截面仅约束Z方向，刚凸的运动通过控制与端面耦合的参考点RP-1实现。切向磨损仿真加载过程包含2个分析步，如图1所示。第1个分析步仅保留参考点Y方向的自由度，同时施加法向的压力载荷；第2个分析步保持压力载荷恒定的同时施加切向周期变化的位移载荷。

刚凸以及包壳基体材料为锆合金，弹性模量为95.6 GPa，泊松比为0.332 5；涂层材料为铬，弹性模量为258.9 GPa，泊松比为0.22。

磨损过程通常可分为3个阶段。首先是跑合磨损阶段：新的摩擦副在运行初期，由于对偶表面的表面粗糙度值较大，实际接触面积较小，接触点数少而多数接触点的面积又较大，接触点粘着严重，因此磨损系数较大；其次是稳定磨损阶段：这一阶段磨损缓慢且稳定，磨损系数保持基本不变；最后是剧烈磨损阶段：经过长时间的稳定磨损后，由于摩擦副对偶表面间的间隙和表面形貌的改变以及表层的疲劳，其磨损系数急剧增大。本文中主要研究包壳管-刚凸失效前的磨损行为，故仅考虑前2个磨损阶段磨损系数的变化情况。

通过已开展的试验发现，当磨损周次达到30万周次时，磨损进入稳定磨损阶段。通过试验数据拟合得到包壳管-刚凸切向磨损系数与磨损周次的关系式如下：

式中：k为磨损系数；为前30万周次的平均磨损系数，通过试验得到；N为磨损周次（万次）。

2 磨损有限元实现

在进行微动磨损的有限元仿真时，需要对接触面节点坐标进行控制以保证磨损表面符合实际情况，故采用一种适用于微动磨损的磨损模型来计算每次的磨损量。选择合适的磨损模型是微动磨损仿真的关键，通常有2种磨损模型用来预测磨损过程，即Archard模型和能量模型。当接触面间的摩擦因数不是定值或者当接触面间产生部分滑移时，Archard模型很难对微动磨损进行合理的定量计算。能量模型的优点在于其磨损系数不受位移幅值以及摩擦因数大小的影响，测量更加准确。但由于需要获得大量的摩擦切应力-滑移量数据，且要求相当大的采样密度，再通过积分获得能耗值，这种方法很难实现，应用偏少。

选取Archard模型作为磨损计算模型。其磨损深度的计算式如下：

式中：h（x）为位置x处的磨损深度；ΔN为加速次数；k为磨损系数；p（x）i表示位置x处第i增量步的局部接触压力；Δs（x）i表示位置x处第i增量步的局部相对滑移增量。

通过ABAQUS主程序计算可以得到局部接触压力和局部相对滑移量，通过变量CPRESS和CSLIP传递给UMESHMOTION子程序。子程序根据加速次数以及磨损系数计算出对应的局部磨损深度并将值返回给ABAQUS主程序。结合ALE自适应网格技术更新轮廓，微动磨损仿真流程如图3所示。

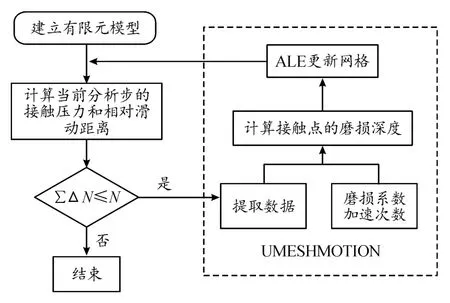
图3 微动磨损仿真流程

3 模型验证

核电领域通常规定，当包壳管磨损深度达到壁厚的10%时即认为已失效，所以包壳管-刚凸切向微动磨损研究主要关注最大磨损深度。有限元计算结果与试验结果见图4所示。有限元计算结果与试验结果吻合较好，说明本文中建立的有限元计算模型在一定程度上能够表征包壳管-刚凸切向微动磨损行为。

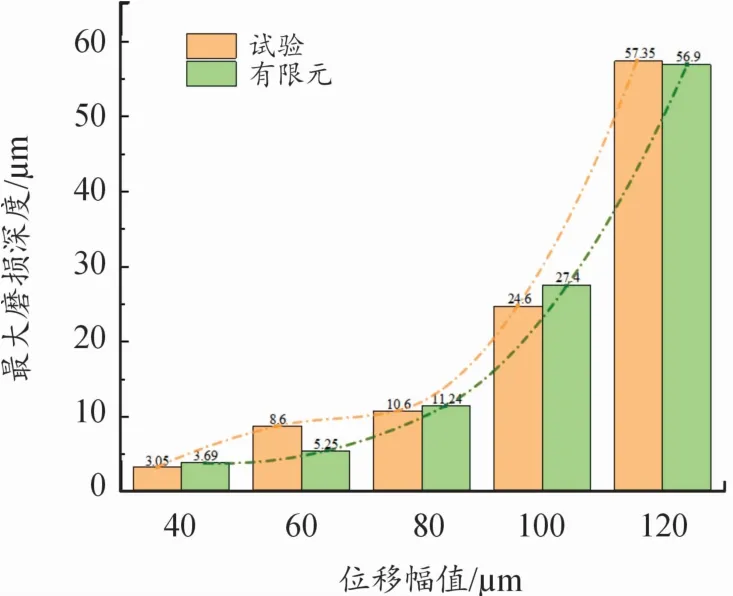
图4 试验／有限元最大磨损深度

4 磨损结果分析

4.1 F-D曲线

摩擦力-位移曲线（F-D曲线）是微动磨损中最基本的信息，曲线形状可以用来描述接触面间的相对运动关系。如图5所示，法向预紧力为50 N，位移幅值为40、60、80μm时F-D曲线为椭圆形，如图5（a）所示，此时微动运行处于部分滑移状态，且随着位移幅值的增大滑移区逐渐增大；当位移幅值为100、120μm时F-D曲线为平行四边形，如图5（b）所示，此时微动运行处于完全滑移状态。

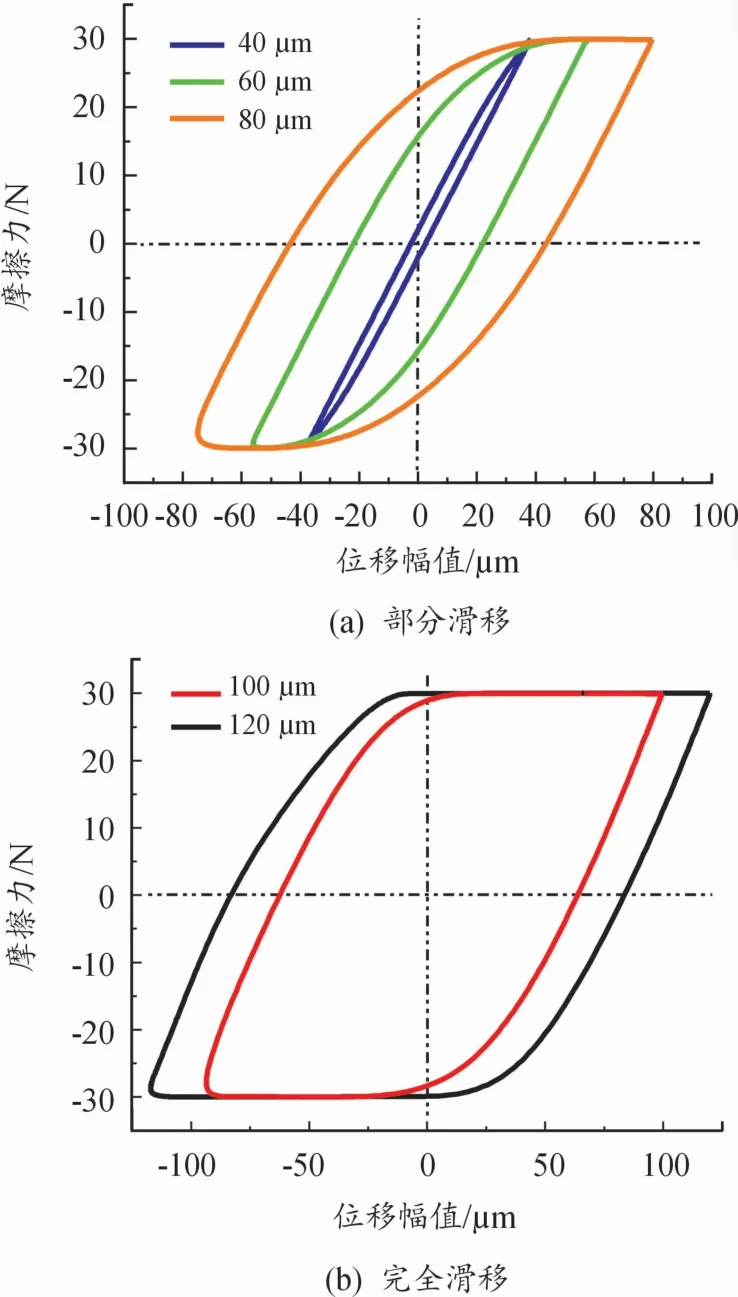
图5 F-D曲线

4.2 磨损轮廓

预紧力50 N、磨损2万周次时，不同位移幅值的磨损轮廓如图6所示。位移幅值越大，磨损宽度和深度越大。

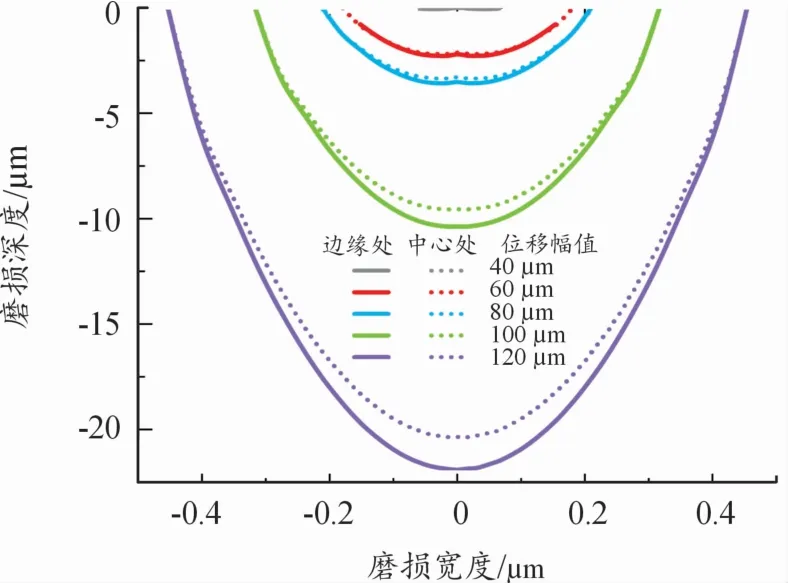
图6 磨损轮廓示意图

沿轴向方向接触压力不是均匀分布的，不同预紧力载荷作用下沿轴线方向的接触压力分布如图7所示，接触边缘处的接触压力均大于接触中心处，所以沿轴线方向（Z方向）包壳-刚凸接触边缘的磨损深度均大于接触中心处。

图7 接触压力分布

4.3 最大磨损深度

不同位移幅值、不同预紧力、磨损周次为5万次下有限元计算的最大磨损深度如图8所示。在部分滑移和完全滑移状态下，预紧力越大，位移幅值越大，对应的最大磨损深度越大；完全滑移状态下的最大磨损深度显著大于部分滑移状态下的最大磨损深度。

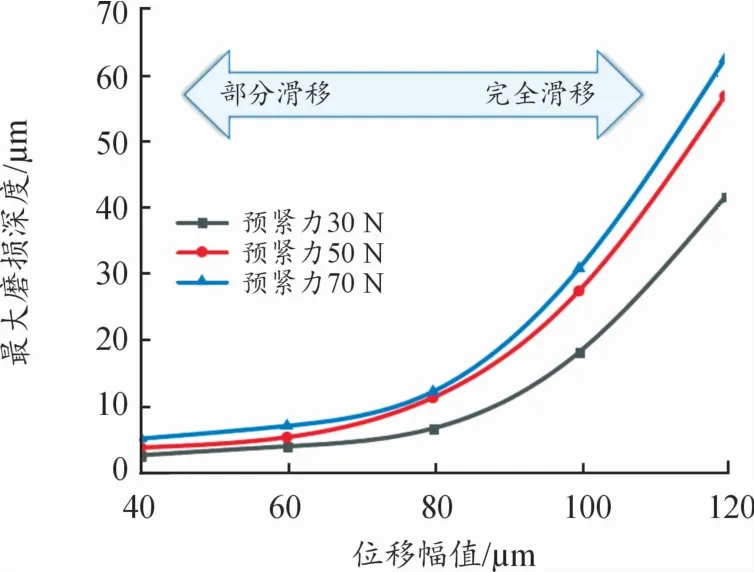
图8 最大磨损深度（5万磨损周次）

预紧力为50 N、不同位移幅值以及不同磨损周次下有限元计算的最大磨损深度如图9所示。相同预紧力、位移幅值作用下，磨损周次越大，最大磨损深度越大；随着磨损周次增加，磨损速率逐渐减小后趋于平缓，且位移幅值越大，磨损稳定阶段的磨损速率越大。

图9 最大磨损深度（50 N预紧力）

5 结论

1）法向预紧力为50 N，位移幅值为40、60、80 μm时微动运行处于部分滑移状态，当位移幅值为100、120μm时微动运行处于完全滑移状态。

2）沿轴线方向（Z方向）包壳-刚凸接触边缘的磨损深度均大于接触中心处，因为接触中心为面接触，而接触边缘为线接触，其接触应力更大。

3）在部分滑移和完全滑移状态下，预紧力越大，其接触压力越大，位移幅值越大，相对滑移距离越大，对应的最大磨损深度越大；完全滑移状态下的最大磨损深度显著大于部分滑移状态下的最大磨损深度。

4）相同工况下磨损速率随着磨损周次逐渐减小并趋于稳定，相同预紧力下，位移幅值越大，其稳定磨损阶段的磨损速率越大。