低频噪声测量技术在电子元器件测试系统中的设计应用

贺养芬，张艳

（陕西恒太电子科技有限公司，陕西西安，710100）

0 引言

低频噪声是电子元器件中常见的干扰源之一，对系统的性能和稳定性产生重要影响，在电子元器件测试系统中，准确评估低频噪声的质量和性能至关重要[1]。将低频噪声测量技术应用于测试系统的设计中，旨在消除外部干扰源，确保系统稳定性和一致性，并提供可靠的测试结果[2]。基于上述需求，本文设计了一套有关低频噪声测量技术应用于电子元器件的测试系统，通过设计系统总架构、硬件及软件相关内容，并对系统进行测试，证实了系统性能可在一定范围内保持一致，并且受到较小的波动干扰，能够准确评估电子元器件的低频噪声特性。通过设计应用该系统，以期为后期系统的研发、优化和维护提供一定支持。

1 系统总架构

为确保对电子元器件能够在低频噪声测量技术下获得准确测试，需要设计一个具备高度输入灵敏度的测试系统。基于低频噪声测量技术在电子元器件测试的设计系统总架构见图1。

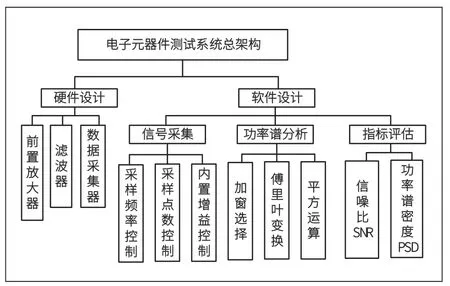
图1 系统总架构

考虑到低频噪声的微弱特性，硬件设计方面需考虑使用前置放大器、滤波器、数据采集器等[3]。为准确分析和处理低频噪声信号，采用滤波器去除高频噪声成分，提取噪声功率谱密度。在数据采集方面，需要选择合适的采样率和采样精度，以确保对低频噪声进行充分、准确的采样。同时，在数据处理方面，要进行有效的噪声分析和统计处理，以获得可靠的测量结果。

2 硬件设计

在电子元器件测试系统中，进行低频噪声测量的设计应用涉及信号处理电路设计。其中，前置放大器是一个关键组件，为满足低噪声特性、高增益和较好的性能指标，并考虑输入阻抗和放大倍数的要求，测试系统选取了LT1115 运算放大器，LT1115 是一款超低噪声和高精度的运算放大器，其具有极低的噪声和失真特性，非常适合用于低频噪声测量应用，其噪声系数很低，在工作频率范围内可以提供出色的信号质量。为保证测量准确性，还需要采取降低噪声和失真的方法，因而选用了BFP640FESD 低噪声元件和LTC1569优化边带滤波器。BFP640FESD 是一种专为低噪声应用设计的NPN 晶体管，具有极低的噪声指标和优良的线性特性。使用LTC1569 边带滤波器可以进一步降低系统中干扰和失真的影响，提供更加清晰和准确的测量结果。数据采集器采用NI USB-6210，在低频噪声测量系统中，NI USB-6210可用于接收来自测试电路的信号，并将其转换为数字信号进行处理。其具有高分辨率和低噪声特性，能够有效地保留信号的细节和准确度。LT1115 运算放大器需要对输入信号进行偏置，确保放大器工作在合适的工作点，满足低频噪声测量系统的要求。已知测试噪声电压为10nV，噪声电流为1pA，在设计过程中需要考虑上述噪声参数，并在系统中采取相应的措施来最小化其影响，以保证测量结果的准确性。偏置电路设计如图2 所示。

图2 偏置电路设计图

在偏置电路中，设置一个双向开关。双向开关在调节工作电流时充当测量和调节的功能，在噪声提取过程中起到连接电路的作用。当开关与3 连接时，能够通过电流表读取到工作电流信息。通过调节滑动变阻器的阻值，可将电流调节到预定值1mA。当电流调节完成，则将开关与1 进行连接，继续进行噪声提取工作。

3 软件设计

3.1 信号采集

使用针对特定数据采集设备的API，可以设置采样频率。首先，确定所需的采样频率，以Hz 为单位。随后，使用采样频率计算每个采样点的时间间隔，即采样周期（T）的倒数，见式（1）。

式中，T为采样周期，n为采样频率。根据采样周期和数据采集时长，可计算出采样点的总数，见式（2）。

式中，Σm为采样点总数，t为数据采集时长，T为采样周期。在根据采样周期和数据采集时长计算采样点的总数时，通过确定数据采集时长t，同样可以使用公式计算出采样点的总数，见式（3）。

式中，数据采集时长t为采集数据的总时长，以（s）为单位；采样频率n为每秒采样的次数，以（Hz）为单位。将数据采集时长和采样频率代入上述公式，即可得到采样点总数Σm。在数据采集过程中，为适应不同的信号强度或噪声水平，需进行内置增益控制。通过调整输入信号的增益，可以优化信号质量，使得采集到的数据更具有可靠性和准确性。

3.2 噪声功率谱密度算法

3.2.1 加窗选择

为减小频谱泄漏的影响，在进行傅里叶变换之前，需要对采集到的数据应用一个窗函数。系统选用了汉明窗（Hamming Window）函数用于频谱分析和信号处理。汉明窗的数学表达式见式（4）。

式中，nW为窗函数在索引为n的位置上的值，N为窗口长度。汉明窗在窗口两端具有较小的幅度，可以减少频谱泄漏的问题，同时，汉明窗在窗口内部可平滑过渡，能够提供更为优质的频率分辨率。

3.2.2 傅里叶变换

完成加窗后，对经过窗函数加窗后的数据应用傅里叶变换（FFT）。FFT 是一种高效计算傅里叶变换的算法，给定一个长度为N的离散信号序列xn，其中n=0,1,...,N-1。其FFT 结果Xk定义见式（5）。

式中，Xk为离散频率域上的复数结果，k是频率下标，取值范围是0 到N-1。xn是时域下标，也就是信号的采样点索引，取值范围也是0，…N-1。具体而言，对于每个频率下标k，公式右侧的求和表示了对时域信号进行加权和的计算。乘法项xnge（-jg2pgkgn/N）中，xn是时域信号序列的采样值，e是自然对数的底数，j是虚数单位，j2=-1 。通过对时域信号序列进行逐点操作，计算每个频率下标k对应的复数结果Xk，可得到信号的频域表示。对输入信号序列xn进行重新排列，使得序列中的元素按位反转顺序排列，可为后续的迭代计算做准备。同时，将原始序列xn分为偶数下标和奇数下标的两个子序列：xeven（n）和xodd（n），即将原始序列按序号的奇偶性分成两个子序列。此时，对两个子序列xeven（n）和xodd（n）分别进行FFT 计算，可以递归地应用FFT 算法，即对子序列再次进行重新排列计算。将所得子序列的FFT 结果xeven（k）和add（k）进行组合，得到整个序列的FFT 结果Xk。通过利用FFT 快速傅里叶变换公式，可将时域信号转换为频域信号。

3.2.3 平方运算

对于傅里叶变换后得到的频域结果Xk，分别计算出每个频率k对应复数结果实部和虚部的平方。平方运算公式见式（6）。

式中，Xreal（k）为X（k）的实部，Ximag（k）为X（k）的虚部。由此得到的Xsquared（k）就是频域上的平方结果，表示了信号在不同频率下的强度或振幅的平方。X（k）是复数形式的，其平方结果Xsquared（k）也是复数形式。通常在系统测试中，测试关注的是其功率谱密度（power spectral density），即信号在不同频率下的功率，则得出公式见式（7）。

式中，Power（k）为频率k对应的功率谱。Xreal（k）和Ximag（k）分别为傅里叶变换结果X（k）的实部和虚部。计算功率谱密度的目的是测量信号在不同频率下的功率或能量。通过将实部和虚部的平方相加，可以得到信号在该频率下的总功率。

3.3 噪声指标评估

为了对信号质量和噪声特性进行定量评估和比较，首先需确定测试系统评估噪声指标，系统选取了信噪比（SNR）、噪声功率谱密度（PSD）作为评估对象，并使用所选的噪声指标对信号进行计算。SNR 通过比较信号的能量与噪声的能量进行计算；PSD 通过对信号进行傅里叶变换并计算频率域上的功率谱密度来进行计算。对于给定的信号样本或数据，可以通过对信号中每个采样点的幅度平方进行求和，计算信号的能量。通过将信号能量与噪声能量的比值，可以得到信噪比的计算结果。SNR 表示信号与噪声的相对强度。假设信噪比为SNR，则SNR 指标评估公式见式（8）。

式中，Ex为信号的能量，En为噪声的能量。取信号能量与噪声能量的比值对数，并乘以一个常数10，可以得到信噪比的计算结果。式（8）计算出的信噪比结果，需将其转换为以分贝（dB）为单位。

计算噪声功率谱密度（PSD）需对信号进行傅里叶变换来计算频域上的功率谱密度。首先，对信号进行采样得到离散样本xn，然后对其应用快速傅里叶变换（FFT）。假设频域上的功率谱密度为PSD，则噪声功率谱密度（PSD）表示见式（9）。

式中，xn是一个离散时间域的信号序列，FFT[xn]为对xn进行傅里叶变换， |FFT[xn]|2为表示取FFT结果的模的平方。噪声功率谱密度（PSD）用于描述信号中各个频率分量的功率强度。其提供了一个在频域上分析信号的方法，可以帮助系统理解信号中不同频率成分的贡献以及噪声的特性。

4 系统测试

4.1 测试准备

在开始进行测试工作时，需充分考虑测试时间，经长时间的测试，可以减少测量误差和随机噪声对结果的影响。测试用例见表1。

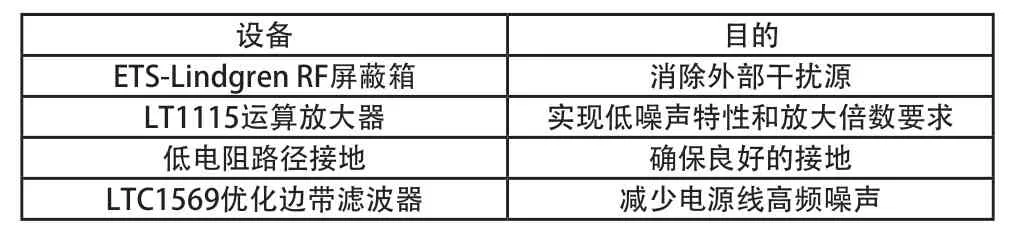
表1 测试准备用例

为确保测试环境的稳定性和一致性，消除任何可能引入噪声或影响测试的外部干扰源，测试期间采用了ETSLindgren RF 屏蔽箱。考虑低噪声特性和放大倍数的要求，选用了LT1115 运算放大器。同时，采用低电阻路径将设备接地，以确保所有测试设备和被测试元器件都能够良好的接地。此外，该系统使用了LTC1569 优化边带滤波器以减少电源线的高频噪声，防止噪声通过电源传播到测试系统中。

4.2 测试结果

通过计算和分析信噪比SNR 以及噪声功率谱密度（PSD），可以评估信号的强度或质量。经测试，SNR、PSD 测试数据见表2。

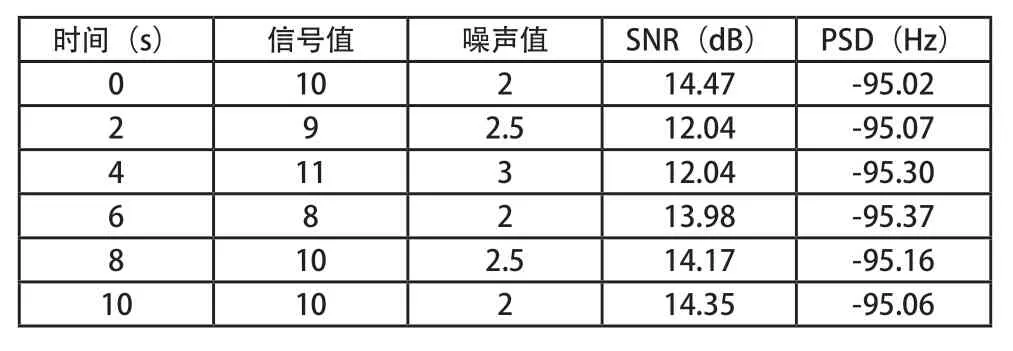
表2 信号质量测试结果

由表1 数据可知，不同时间点的SNR 值都在12～14之间。其中，时间初始SNR 为14.47，时间2s 和时间4s的SNR 均为12.04，时间6s 的SNR 为13.98，此后时间段SNR 开始接近初始值；在噪声功率谱密度（PSD）中，尽管PSD 值有变化，但变化并不剧烈。PSD 值在-95.02 dB/Hz～-95.37 dB/Hz 之间波动，差异相对较小，且所有的PSD 值都是负数，接近-95 dB/Hz，表示噪声水平相对较低。以上数据证实了时间范围内，噪声功率密度保持相对稳定。由此，可得出结论，低频噪声测量技术在电子元器件测试中信号质量总体良好，并且在一个相对稳定的范围内波动。

5 结束语

低频噪声测量技术在电子元器件测试中的应用，为评估信号质量和保证系统性能提供了重要手段。通过消除外部干扰源、选择合适的设备和优化信号处理算法，该技术能够准确评估信号质量。通过系统测试数据表现，观察到信号质量总体良好且在相对稳定的范围内持续变化。