信号分离系统设计

陈佳星，王子玉，王玉林

（辽宁工程技术大学 电气与控制工程学院，辽宁葫芦岛，125105）

0 引言

根据2023 年全国大学生电子设计竞赛的参赛情况，该竞赛规模持续扩大，共有1134 所高校和20939 支队伍报名参加[1]。竞赛题目类型涵盖了控制、测量、信号处理等多个领域。其中，2023 年的竞赛中涉及了信号处理的H 题信号分离装置。

该系统以32 位单片机STM32F407VET6 为控制核心，通过快速傅里叶变换（FFT）分析获得两个主频，并利用AD9833 模块复现原信号。同时，辅以频率加权算法、压控恒温晶振（VC-TCXO）、鉴相模块AD8302 等组件，成功实现了信号分离系统。此系统不仅在竞赛中圆满完成了所有任务，还为理论教学提供了实践案例和操作平台，深化了对理论教学的理解，对教学产生了积极的影响。

1 系统总体方案设计

信号分离系统主要对两个三角波或正弦波叠加后的信号进行分离。系统主要包括四部分：包括主控（STM32F407VET6单片机）、波形复现、频率反馈和人机交互。如图1 所示。

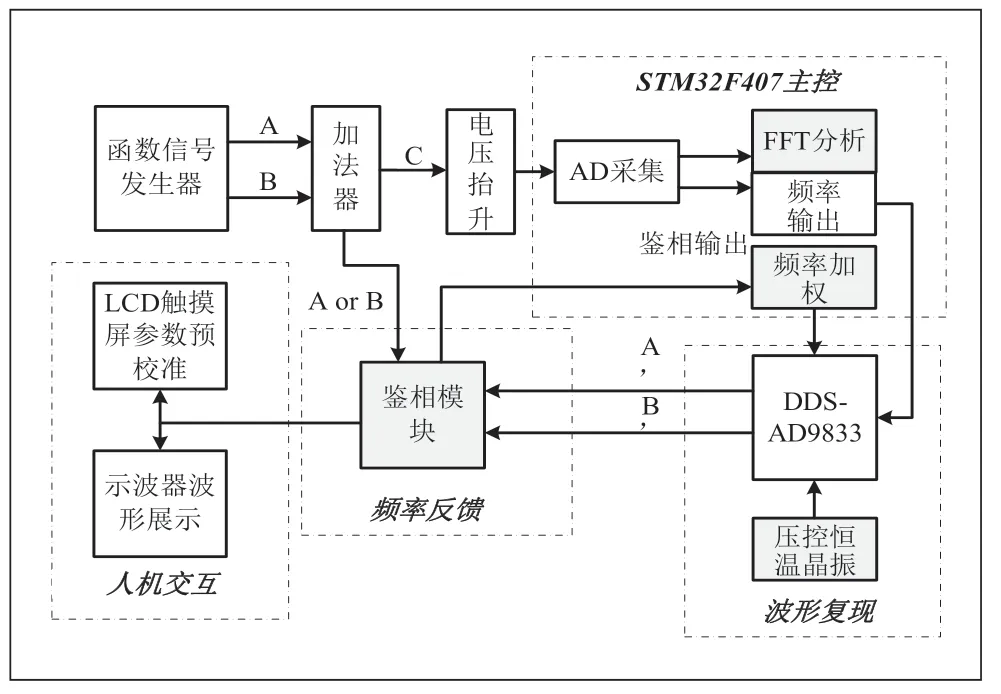
图1 系统总体框图

该系统的主控部分负责进行模拟信号的采集，并通过FFT 分析得到两个最大基频的三至五次谐波。同时，它还执行频率加权算法，以提高AD9833 的频率精度。系统采用了STM32F407VET6 单片机作为核心处理器，通过相位锁定环（PLL）倍频[2]，将主频提升至168MHz。另外，此单片机还配备了3 个12 位精度的快速模数转换器，最高采样频率可以达到7.2MHz，根据香农定理[3]7.2MHz 远大于系统要求的最大频率100kHz，完全满足系统的需求。

系统采用AD9833 实现信号的复现。传统方法直接使用AD9833 复现高频信号时，由于频率精度不足，会导致与原信号同时显示时出现频率漂移现象，不利于信号的观察。因此，系统采用了10MHzVC-TCXO，并结合频率加权算法来提高频率精度，最大程度地减小温度对结果的影响。

为了解决直接使用AD9833 进行高频信号复现时频率精度不足、导致与原信号显示时出现漂移现象的问题，系统引入了频率反馈部分。该部分将原信号A 和B 作为输入信号，与信号A'和B'进行鉴相，得到二者之间的相位差。最后，通过频率加权算法实现对系统的闭环控制，以提高频率精度并减小温度对结果的影响。

系统还加入了人机交互部分，用于进行初始参数的预校准并完成信号相位的改变。人机交互部分由液晶显示屏触摸屏和数字示波器组成。由于不同型号的数字示波器和函数信号发生器在对信号进行处理时都存在一定的硬件误差，因此根据液晶显示屏触摸屏的提示，对复现信号进行频率补偿，以实现与原信号同屏显示而不产生漂移现象的目的。

2 系统理论分析与运算

在解决信号分离问题的过程中，本系统采用了FFT、VC-TCXO、频率加权算法和频率反馈等基础理论。首先，将采集到的信号进行FFT 变换，以获取其频谱分布，并分析得到主频。然后，利用AD9833 进行波形复现，结合外部10MHz VC-TCXO 晶振来最小化温度对系统的影响，并通过频率加权算法来提高频率精度。同时，设计了硬件校准补偿模块，以确保信号在频率显示过程中无漂移。系统还利用鉴相模块AD8302 与原始信号进行比对，根据AD8302 输出的直流量来不断调整相位，从而实现对输出信号A'和B'初相位差的调节。最后，根据信号C 的频谱图，观察其三次至五次谐波的存在，以确定三角信号的存在，并进一步实现混叠信号的分离与复现。具体的系统流程如图2 所示。

图2 整体流程图

2.1 FFT 频谱分析

FFT 是一种高效的数字信号处理算法，用于将时域信号转换为频域信号，以便分析信号的频谱特征[4]。FFT 算法通过将N 点离散傅里叶变换（DFT）问题分解为多个规模更小的DFT 问题来实现快速计算。它利用频域的对称性和周期性，减少了重复计算的次数，从而大大提高了计算效率。与暴力求解DFT 的复杂度O（N^2）相比，FFT 算法的复杂度为O（NlogN）[5]。利用FFT 对不同信号进行频谱分析时，得到的频谱图差异很大。对于幅值相同、初相位相同的三角信号和正弦信号进行FFT，如图3 所示。

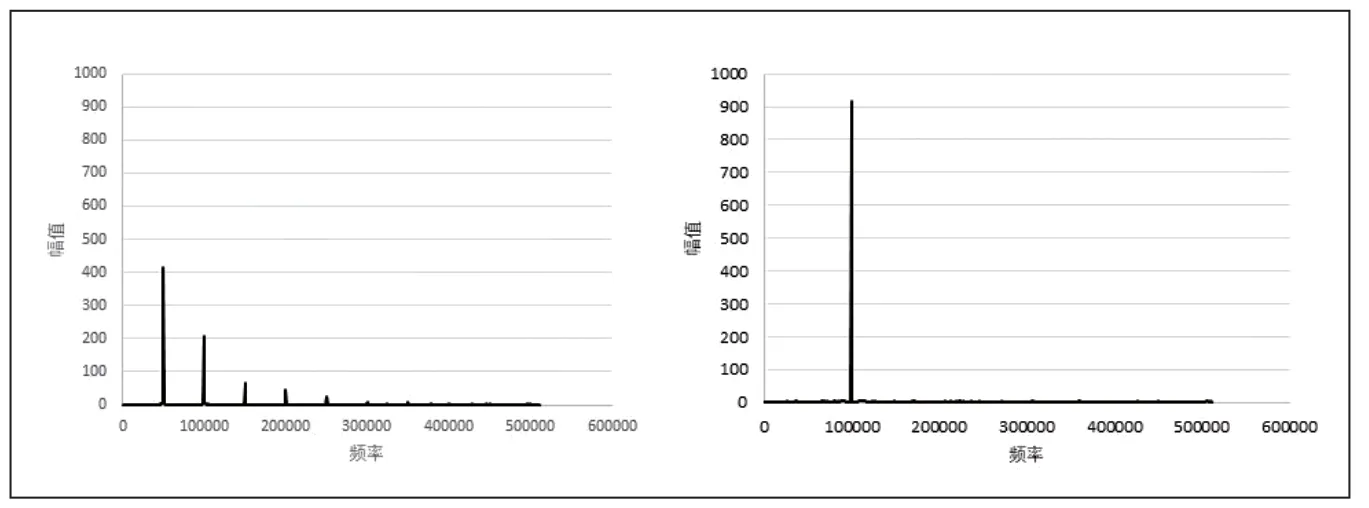
图3 三角信号（左）和正弦信号（右）的频谱分析

由图3 可以观察到它们的频谱图有明显差别。正弦信号只有一个主频，并且幅值接近于原信号，而三角信号除了主频之外，还存在多个谐波，并且谐波的幅值递减。通过区分这两种信号的频谱特征，可以提取主频并将其输入到AD9833 中，以实现波形的复现。

2.2 频率精度提高

2.2.1 VC-TCXO

外接一个压控恒温晶振（VC-TCXO）可以提高AD9833的精度[6]。VC-TCXO 能够提供稳定的振荡频率，使电子设备能够准确计时和进行时间同步。它通过控制电压来调整晶振的温度补偿，内置的温度补偿电路能够实时监测温度变化，并通过调整电压来修正晶振，以在不同温度下提供稳定的频率输出，从而实现频率的稳定性。

对于AD9833 而言，其频率寄存器为28 位，当主频时钟为25MHz 时，精度为0.1Hz[7]；当外接一个10MHz 的VC-TCXO 作为AD9833 的同步时钟源时，其精度将提高到0.03725Hz。

其中，fjz为VC-TCXO 的频率，a为寄存器位数。

2.2.2 频率加权算法

为了提高精度，可以结合频率加权算法来进一步提升AD9833 的精度。频率加权合成算法将目标频率的总时间分为64 等分，每个等分对应一个时间权重。在选择待加权频率时，选取距离目标频率最近的两个频率，并按照时间权重的比例将时间分配给它们，在一定时间内轮流输出这两个频率。通过这种方式，DDS 的频率精度可以提高到0.03725/64=0.00058203125Hz。如图4 所示。

图4 频率加权算法示意图

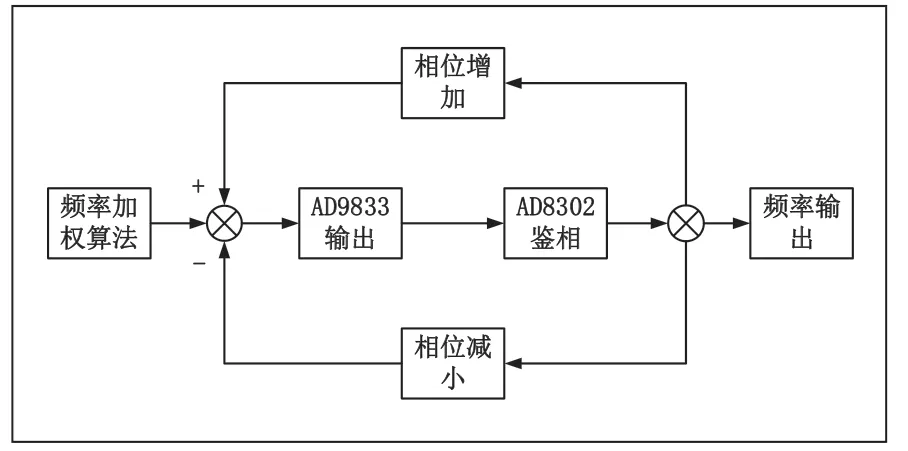
图5 频率反馈控制系统

通过将10MHz VC-TCXO作为DDS的两路同步时钟源，并结合频率加权合成法，可以进一步提高波形复现的精度。即使达到了精度要求，由于数字示波器本身存在误差，难以避免波形漂移现象的发生，尤其是在需要将两个信号进行同频显示时。因此，需要设计硬件校准方法，以实现稳定且不发生漂移的同频波形显示。

2.2.3 硬件校准——频率补偿

AD9833 的精度对信号复现具有重要影响，同时数字示波器对其也有一定影响。数字示波器的标准信号（频率）相对较为稳定，如Tek2465 数字示波器，其校准频率误差优于0.1%。通过在屏幕上进行校准和比较，可以将误差减小到1%～2%的范围[8]。为了解决这个问题，在人机交互部分设计了硬件校准方法，使人工干预输出频率成为可能，从而降低了数字示波器误差的影响。不同型号的数字示波器对不同频率信号的处理程度存在差异，因此换用其他型号数字示波器对不同信号分离时，都需要进行硬件校准，以将数字示波器本身的影响降至最低，以适应更多的应用场景。

2.4 频率反馈

由于AD9833 内置移相功能，因此，为了实现系统的闭环控制，并提高移相的准确度，本设计引入了鉴相模块——AD8302。该模块的输入为原始信号作为参考信号，以及复现信号作为测试信号，通过比较两者的相位差来实现准确的移相控制[9]。同时，设计了两路反馈机制，当相位差大于零时，系统进入负反馈回路增加高频率字时间权重占比，当相位差小于零时，系统进入正反馈回路减少低频率字时间权重占比。通过不断修正相位差，直至满足所需的精度要求。最后，通过频率加权算法完成对系统的闭环控制，确保系统的稳定性和准确性。

在进行混叠信号的精确分离时，准确识别混叠信号的主频并成功复现仅仅是信号分离工作的一部分。此外，系统还需要能够准确辨别信号的类型。例如，常见的信号类型包括正弦信号、三角信号等。这意味着系统需要能够对输入信号进行特征提取和分类，以正确地识别信号的类型。这样才能有效地实现对混叠信号的完整分离，确保分离后的信号能够准确地还原原始信号的特征和性质。

2.5 三角波和正弦波的混叠识别

由2.1 可得，对正弦信号与三角信号做FFT 后，所得到的频谱会有明显的区别。为简化识别的难度，观察主频的三次、五次谐波存在与否便可区分三角信号与正弦信号。尽管如此，当两信号的频率相同的时候，只观察其三次、五次谐波也并不能够将两种信号区分开。因此，需要分成两种情况来进行判别：两信号的频率相同和两信号的频率不同。

2.5.1 两信号频率相同

当两个信号的频率相同时，通过进行FFT 得到的频谱图中只会出现一个主频。当这两个信号都是正弦信号时，由于没有谐波成分的存在，可以确定它们是正弦信号。当这两个信号都是三角信号时，会出现三次和五次谐波。当这两个信号一个是三角信号，一个是正弦信号时，同样会出现三次和五次谐波。为了区分这两种情况，比较主频的幅值大小是必要的。经过多次测量和实验，发现具有相同频率的三角信号和正弦信号的频谱中主频的幅值是不同的，因此当两个主频的幅值相同时，可以确定为两个三角信号；而当两个主频的幅值不同时，则可以确定为一个三角信号和一个正弦信号。

2.5.2 两信号频率不同

当两个信号的频率不同，经过FFT 频谱分析后会得到两个主频。根据2.1 的结论可知，正弦信号的频谱只有一个主频而没有谐波，而三角信号的频谱除了主频外，还会有其他多次谐波。因此，只需观察频谱中是否存在三次和五次谐波，就可以区分正弦信号和三角信号。图6 为通过Matlab进行混叠信号仿真的结果。

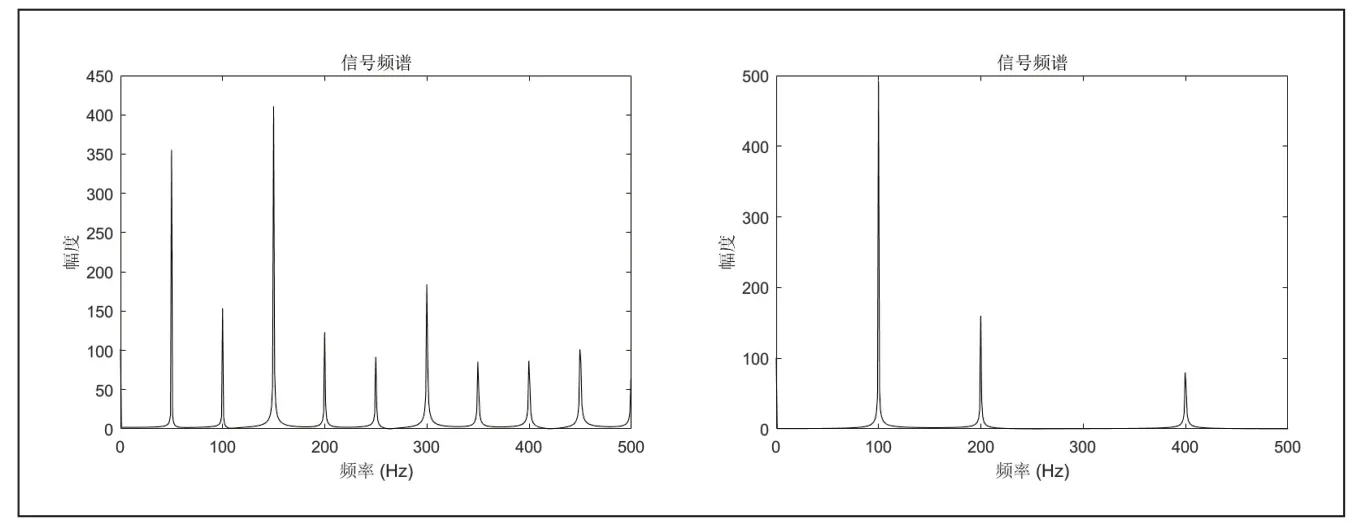
图6 两个三角信号（左）、正弦和三角信号（右）

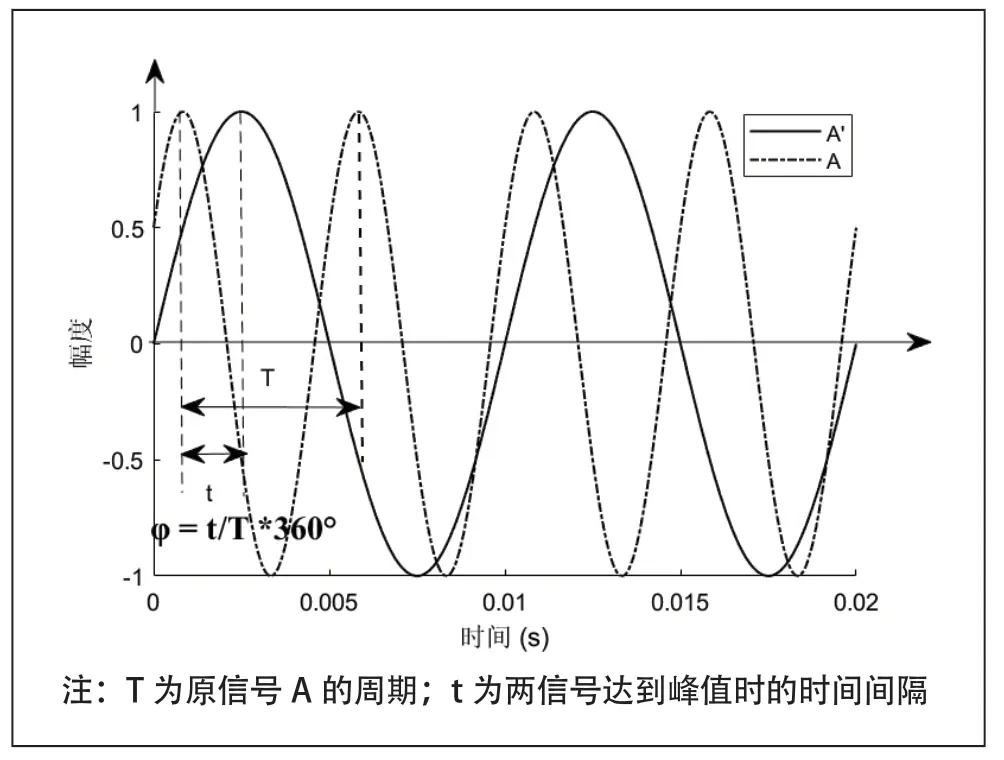
图7 初相位差图示

3 结果与分析

为了验证系统的可行性，本研究对0～100kHz 范围内的任意正弦波和三角波进行叠加，然后对叠加后的信号进行分离和相位改变，并观察分离后的信号与原信号在同一双踪数字示波器上显示时的漂移情况。为了方便测试，本研究采用双通道函数信号发生器作为信号源，输出原始信号A 和B，并使用双踪数字示波器将复现后的信号和原始信号同时显示，以观察信号复现和相位改变后的效果。

3.1 混合正弦、三角信号的叠加分离

通过使用双通道函数信号发生器，产生两个正弦信号A和B，并将它们通过加法器叠加得到了信号C。在单位频率为5kHz 和1kHz 的情况下改变信号A、B 的频率。通过人机交互部分观察本系统对信号C 的分离结果。其中，以单位时间内的周期漂移数量（T/s）作为衡量漂移程度的指标X。此外，频率相近的两个信号叠加对系统分离结果扰动最大[10]，由此，实验记录在这类频率下的一些具有代表性的数据。

表1 信号为A，B为三角和正弦的分离情况

表2 信号A，B为三角的分离情况

根据测试结果，系统在频率确定方面表现出色，即使在频率相差很小的情况下也几乎没有误差。此外，在提高频率精度方面，系统在分离两个三角信号时，波形漂移情况相对稳定，保持在0.1～0.15 周期/秒范围内。然而，在分离正弦信号和三角信号混叠信号时，波形漂移情况相较前者增加了约0.02 周期/秒，但仍然满足了实际需求。

3.2 复现信号的移相

通过以5°为分辨率，在0～180°范围内改变复现信号的相位，利用双踪数字示波器显示复现信号与原信号的实际相位差，与改变的相位进行对比，以评估本系统实现移相功能的误差ε。

其中ε为误差，φ为改变相位，0φ为初相位差。

重复实验多次，记录不同相位变化下的误差情况。

根据实验结果显示，通过以5°为分辨率对信号进行移相，移相误差在大多数情况下能够控制在5%以内，并且只有极少数情况超过了5%。总体而言，这种移相方法符合实际需求。

表3 移相功能测试

4 结束语

本研究基于STM32F407VET6 单片机实现了一个信号分离系统，其中采用AD9833 作为信号复现模块，成功地实现了信号的分离。为了满足系统对频率的要求，本系统采用了VC-TCXO 和频率加权算法，将DDS 的频率精度提高到0.0005Hz，以确保分离得到的信号与原信号能够在同一双踪数字示波器上同步显示而不产生漂移。通过全面的检验和分析，结果表明该系统能够有效地分离任意两个叠加的正弦或三角信号。然而，若要增加信号数量和种类，则需要进一步改进系统。