不同力学激励形式探索La 基非晶合金微观结构非均匀性*

张剑 郝奇 张浪渟 乔吉超

(西北工业大学力学与土木建筑学院,西安 710072)

非晶合金力学行为与其微观结构非均匀性之间本征关联,是固体力学研究领域至今未能很好解决的重要科学问题之一.单一力学激励形式并不能有效地描述非晶合金微观结构非均匀性,特别是结构与动力学的关联.如何探索非晶合金结构信息,须将诸多因素综合,在不同力学激励下研究非晶合金微观结构非均匀性与变形机理.本研究以La62Cu12Ni12Al14 非晶合金为模型体系,利用动态力学分析仪研究非晶合金动态弛豫行为.基于准点缺陷模型,对模型合金体系α 弛豫和β 弛豫进行了分离.借助于拉伸应变率跳实验,探索非晶合金高温流变行为.确定非晶合金塑性流变过程中弹性、滞弹性以及塑性变形的贡献.本研究从非晶合金动态力学弛豫行为和宏观塑性流变行为出发,尝试揭示微观非均匀性对非晶合金在不同激励形式中缺陷的激活、扩展和融合的物理本质.

1 引言

非晶合金是合金熔体通过急速快冷方式形成的一种亚稳态金属材料.与传统金属材料不同,非晶合金并无晶界、位错等结构缺陷,表现出独特的力学、化学和物理性能,如高强度、高断裂韧性、大弹性应变极限、在过冷液相区的超塑性、良好的耐腐蚀性能以及优良的软磁性能等[1–4].传统金属材料微观结构原子周期性排列、具有平移对称性,其变形机制可借助位错或晶界滑移来实现.然而作为长程无序的玻璃材料,传统金属材料“微观结构-宏观力学性能”的研究范式不再适用描述非晶合金力学性能和微观结构之间的关联.研究非晶合金变形机制,构建其力学性能与微观结构非均匀性的本征关联仍是非晶固体力学研究领域尚未解决的重要科学问题之一.

基于已有研究,非晶合金微观结构一般被认为是不均匀的.这种不均匀既包括化学成分非均匀,也包括结构非均匀,需要找到合适的方法进行探测和表征.非均匀性的存在也成为分析非晶合金硬度、强度、韧性及弹塑性等重要力学参量的出发点.实验分析和计算机模拟中发现,非晶合金中存在着纳米尺度的类液体区域[4–8].和周围区域相比,这些类液体区域表现出较低的原子堆积密度、较低硬度和模量、较高的能态、容易剪切变形和容易流动的特性.非晶合金等玻璃态体系中有两个主要的弛豫过程: α 弛豫对应于非晶固体大规模的原子或分子协同运动,β 弛豫被认为是组成分子或原子局限于玻璃中类液体区域的局部运动,然而目前关于β 弛豫的物理起源尚不清晰.Johari[9]于2002 年最早提出机械刚性玻璃,特别是非晶合金中的β 弛豫来源应该是位于松散堆积区域原子的平移运动.Lu 等[10]在研究非晶合金的室温均匀塑性变形时,发现β 弛豫与非晶合金中局部类液区变形单元或流动单元的起始和演化相关.Zhu 等[11]采用球差矫正电镜和调幅动态原子力显微镜,建立了非晶合金结构弛豫动力学与空间结构异质性之间的关联,他们认为空间结构异质性是非晶合金β 弛豫的结构起源.对弛豫行为的研究被广泛证明是研究非晶合金微观结构的有效手段之一.大量研究表明非晶合金β 弛豫与玻璃态材料的诸多基本物理和力学性能存在着密切关联,如形变、晶化、玻璃转变现象等,非晶合金的弛豫机制和变形行为的本源都同其微观非均匀结构关系密切,Yu 等[12]发现非晶合金β 弛豫行为与其脆韧性转变具有同样的物理起源.2012年,Wang 等[13]在对一系列不同β 弛豫行为的非晶合金进行高应变速率加载时,认识到非晶合金黏弹性、塑性变形行为与β 弛豫具有共同的结构起源.通过研究不同塑性和脆性非晶合金快二次弛豫的动力学特征,Wang 等[14]证实了非晶合金塑性与其“快β 弛豫 (fast β relaxation)”弛豫谱强相关.更为重要的是,借助于低温压缩实验,已经证实了激活这种快二次弛豫将会诱导多重剪切带的形成,进一步使得非晶合金表现出明显的快β 弛豫附近的塑性-脆性转变.因此,对动态弛豫行为的研究有助于理解非晶合金变形过程的物理本质.

非晶合金的塑性应变高度集中在纳米厚度的剪切带中,剪切带中的某个局部位置可能成为裂纹形成的潜在缺陷,这通常会导致材料灾难性的失效.研究表明非晶合金形变高度局域化的特征来源于其微观结构非均匀性[4,15].Liu 等[16]发现Pd82Si18非晶合金在弯曲实验后,在跨尺度 (原子尺度、纳米尺度和微米尺度)范围分层结构非均匀性得到增强,塑性变形过程中,结构发生多尺度协同结构重排.Fan 等[17]基于能量势垒图,推导了Cu56Zr44原子级剪切模量分布,揭示了结构不稳定性是由于具有低局部剪切模量的原子聚集所致.Wang 等[18]通过Cu46Zr36非晶合金原子模拟揭示了纳米尺度上高度非均匀的高斯型剪切模量分布.

为建立非晶态固体的微观结构信息与其宏观力学行为之间的内禀性关联,自由体积模型[19]、流变单元(flow units)模型[20,21]、剪切转变区(shear transformation zone,STZ)模型[22]、准点缺陷模型[23](quasi-point defects model,QPD)等被用于描述非晶合金的物理和力学行为.其中,QPD 不仅可以用于描述非晶合金微观原子运动,同时可以联系弛豫过程中的微观演化及其变形行为.基于前期研究,本文以La62Cu12Ni12Al14非晶合金为模型合金,通过开展动态力学分析实验和高温拉伸实验,系统研究温度和应变速率对非晶合金黏度的影响规律,采用QPD 通过分离塑性流变过程的弹性变形、滞弹性变形以及塑性变形,推导不同激励下非晶合金的力学响应表达式,研究了非晶合金动态力学分析实验中模量演化过程以及高温流变实验中应力应变关系,尝试从非晶合金微观非均匀性角度揭示其弛豫机制与力学行为的关联,以期为进一步探究非晶合金变形行为的微观物理本源提供参考数据.

2 实验方法

本文选取玻璃形成能力强、热稳定性好的La62Cu12Ni12Al14非晶合金作为模型体系[24],分别通过电弧熔炼-铜模吸铸法和单辊甩带法制备实验所需的块体和条带样品.铸态样品通过X'Pert PRO X 射线衍射仪(X-ray diffraction,XRD)确认其玻璃属性,采用Hitachi DSC 7020 差示扫描量热仪(differential scanning calorimeter,DSC)研究模型合金体系热性能.

材料动态力学行为是指材料在交变应力(应变)作用下应变(应力)的响应.非晶合金作为一种典型的黏弹性材料,可采用动态力学分析仪研究其动态弛豫行为.在交变应力作用下应变响应滞后于应力,其模量在复平面内可表达为E=E′+iE′′,其中实部E′为储能模量,表示材料在变形过程中,由于弹性变形而储存的能量;虚部E′′为损耗模量,则表示材料在变形过程中,由于黏性变形而耗散的能量.损耗模量和储能模量的比值 tanδ=E′′/E′称为材料的损耗因子(也称内耗).

本研究所涉及力学实验均在动态力学分析仪(dynamic mechanical analyzer,DMA TAQ800)上进行.非晶合金动态弛豫行为所采用的样品为块体样品,样品尺寸约为30 mm (长) × 2 mm (宽)×1 mm (厚).采用单悬臂强迫振动模式,恒定实验升温速率3 K/min 及加载频率2 Hz,研究非晶合金储能模量和损耗模量随温度的演化.低于玻璃转变温度的退火实验,将模型体系加热到设定温度373 K,观察储能模量和损耗模量在恒定温度条件下随退火时间演化过程.非晶合金高温拉伸实验(应变率跳跃实验和拉伸回复实验)所采用的样品为条带样品,应变率跳跃实验中,采用1×10–4—7.5×10–4s–1间不同应变速率,研究非晶合金在不同加载应变速率的高温流变行为.对于非晶合金拉伸回复实验,将非晶合金在给定温度395 K 以给定加载速率1×10–4s–1拉伸到不同应变,然后卸载应力并观察模型体系应变随时间演化的应力-应变响应.

3 实验结果

3.1 结构及热力学表征

非晶合金热性能由DSC 测定,图1 为La62Cu12Ni12Al14非晶合金DSC 曲线 (升温速率 20 K/min),其玻璃转变温度Tg为400 K,La 基非晶合金的玻璃态特征由X 射线衍射仪确定,图1 插图为XRD衍射图谱,其为典型的玻璃宽泛的“馒头峰”.结合DSC 和XRD 结果,再次确定了模型合金的玻璃属性.

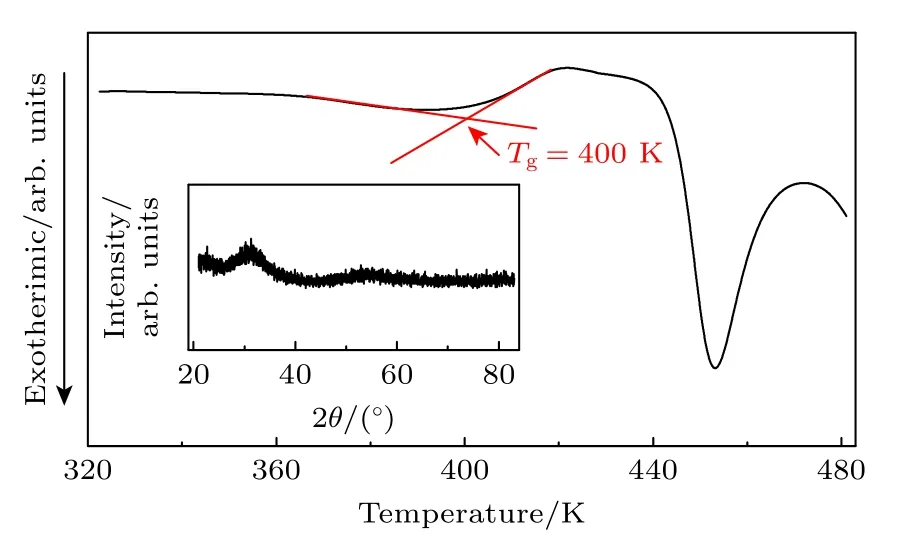
图1 La62Cu12Ni12Al14 非晶合 金DSC曲线 (升温速 率:20 K/min),插图为非晶合金的XRD 衍射图Fig.1.DSC curve of La62Cu12Ni12Al14 amorphous alloy(heating rate is 20 K/min),insert shows the XRD pattern of the amorphous alloy.

3.2 动力学弛豫分析

玻璃形成熔体在冷却过程中,其动态弛豫行为通常会在一个临界温度Tc处由单一的弛豫机制劈裂为两种弛豫形式: α 弛豫和β 弛豫[5,20].对于低温段β 弛豫行为,在不同玻璃体系中表现出不同形式.通常,La 基体系表现为明显的β 弛豫峰(peak),Pd 基体系表现为肩膀峰(shoulder),CuZr 基非晶合金β 弛豫难以被直接观测而表现为α 弛豫的过剩尾(excess wing)[14,25,26].图2 为La62Cu12Ni12Al14非晶合金储能模量和损耗模量随温度的演化(升温速率为3 K/min,加载频率为1 Hz),Eu为室温下未弛豫时非晶合金储能模量.La 基非晶合金表现出其他非晶合金相似动态弛豫特征,其储能模量和损耗模量随温度的演化过程大致可以分为3 个阶段: 1)低温区域(从室温到325 K),归一化储能模量损耗模量基本不随温度发生变化,这表明La 基非晶合金在该温度区间的变形主要由弹性变形主导;2)温度介于325—400 K,储能模量略微下降,不同于典型La 基体系,损耗模量表现为肩膀峰,对于这一现象,Yu 等[27]认为显著β 弛豫峰与所有原子对具有较大相似负混合焓值系统有关,而正的或显著混合焓波动则会抑制β 弛豫,经过实验发现对于具有明显β 弛豫峰的LaNiAl 体系,Cu 含量增大会抑制β 弛豫,导致其向肩膀峰乃至过剩尾转变,非晶合金β 弛豫对应其原子局域运动.由于接近无序密堆结构,并没有复杂的分子间相互作用,金属液体被认为是最简单的玻璃形成液体.在过去十几年研究中发现,β 弛豫是玻璃态的动力学起源.例如,β 弛豫被认为是α 弛豫的前驱,不仅决定结构弛豫行为和玻璃化转变,而且还影响非晶合金的力学行为[21].非晶态材料的α 弛豫呈现出典型的非Arrhenius 性和非指数性,在接近玻璃转变温度Tg时,α 弛豫时间急剧增大,并在Tg处冻结.3)温度升高至400 K 以上时,储能模量大幅降低,损耗模量快速升高再下降,呈现出明显主弛豫(α 弛豫)行为,模型合金体系的主弛豫峰温Tα为439 K,非晶合金α 弛豫对应其原子或分子大规模协同运动,与β 弛豫不同,α 弛豫是一种较慢的弛豫过程,其对应着非晶合金的动态玻璃转变行为[28].

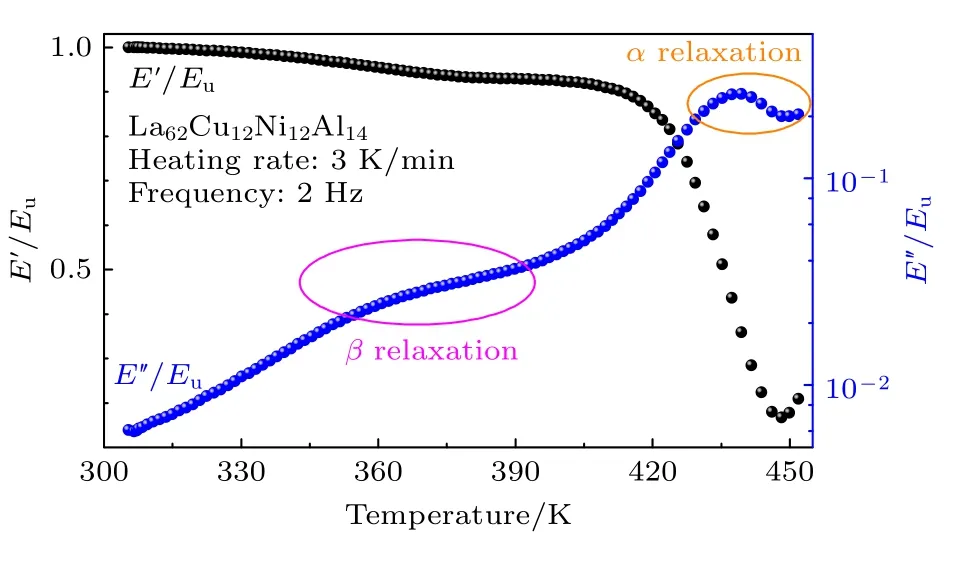
图2 La62Cu12Ni12Al14 非晶合金归一化储能模量E'/Eu 和损耗模量E''/Eu 随温度演化Fig.2.Evolution of the normalized storage modulus and loss modulus with temperature of La62Cu12Ni12Al14 amorphous alloy.

事实上,非晶合金动态弛豫行为具有强烈加载频率依赖性[4].恒定升温速率,以不同加载频率(1,2,4,8 和16 Hz)将非晶合金从室温加热到523 K.图3 为不同加载频率时,非晶合金损耗模量随温度的演化.显然,随加载频率增大,β 弛豫和α 弛豫均向高温段迁移.非晶合金β 弛豫与加载频率之间关系可由Arrhenius 方程描述[21]:f=f0exp(-Eβ/kT),其中f表示加载频率,f0为常数,Eβ表示名义激活能,k为玻尔兹曼常数.

图3 La 基非晶合金在不同加载频率时损耗模量随温度演化,插图为lnf 与1000/T 之间关系Fig.3.Evolution of the loss modulus with temperature in various frequency,insert shows the correlation between lnf and 1000/T.

一般具有明显β 弛豫峰的体系,其β 弛豫激活能可以通过拟合加载频率和峰值温度之间的线性关系得到,对于不明显的“shoudler”型β 弛豫,Yu 等[29]提出了一种计算其激活能的方法,即用β 弛豫的起始温度、结束温度或温度中点代替峰值温度进行拟合,本文采用β 弛豫结束温度进行拟合,拟合结果为图3 插图所示,表明加载频率和β 弛豫结束温度之间线性相关,获得La 基非晶合金β 弛豫名义激活能Eβ=1.11 eV .不同体系非晶合金β 弛豫表现形式不同,但是其本质是一样的,通过对大量非晶合金体系β 弛豫激活能计算,得出非晶合金β 弛豫激活能Eβ与玻璃转变温度Tg之间服从经验公式:Eβ ≈(24±2)RTg[30],其中R为气体常数.玻璃转变温度Tg被视为α 弛豫的特征温度,Eβ与Tg关系表明非晶合金α 弛豫与β 弛豫是密切相关的,在势能景观中可认为α 弛豫对应于大能谷之间大范围的不可逆原子重排,而β 弛豫对应于小能谷之间可逆原子重排,β 弛豫可以认为是α 弛豫的前驱.图4 给出了典型非晶合金体系β 弛豫名义激活能Eβ与玻璃转变温度Tg之间的关系,符合上述经验公式预测,基本线性相关[31–34],基于Arrhenius 方程可知La62Cu12Ni12Al14非晶合金β 弛豫激活能为1.11 eV～31.41RTg,相比于其他典型非晶合金体系,La62Cu12Ni12Al14非晶合金β 弛豫激活能略微高于该经验公式预估范畴.非晶合金β 弛豫激活能可作为衡量微观结构非均匀性和原子移动性可靠指标,β 弛豫激活能较大表明该体系微观结构非均匀性程度较低且原子移动性较差.如前所述,Yu 等[27]认为显著β 弛豫峰与所有原子对具有较大相似负混合焓值系统有关,而正的或显著混合焓波动则会抑制β 弛豫,相比于LaNiAl 体系,Cu 元素的加入引入了较小负混合焓以及正混合焓,阻碍了与β 弛豫相关的弦状构型的形成,从而可能抑制β 弛豫,导致La62Cu12Ni12Al14非晶合金的β 弛豫激活能较高,其局部原子发生重排更加困难.

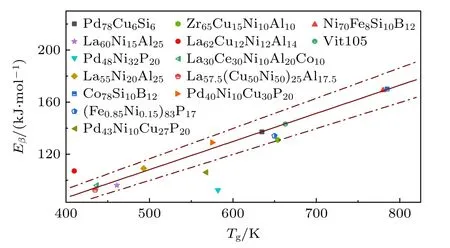
图4 不同体系非晶合金的β 弛豫名义激活能分布[31–34],图中点划线区域为经验公式 Eβ=(24±2)RTg 包围区域Fig.4.Evolution of the β relaxation at different amorphous alloys with the glass transition temperature[31–34],dotted area in the figure is the area surrounded by empirical formula Eβ=(24±2)RTg .

随着对非晶合金物理性能以及力学行为的不断深入研究,对于微观缺陷的猜想与探究已经成为了解非晶合金宏观力学行为、动态弛豫行为和微观结构之间联系的重要切入口,大量模型被提出并被用于描述非晶合金微观结构及其与宏观力学行为的关联[35–39],这些工作因其可以定性或半定量地描述非晶合金微观结构,及其与宏观力学行为的关系而倍受广大科研工作者关注.但是,如何定量研究非晶合金缺陷浓度及其宏观力学行为之间关联仍需进一步探究.Argon 和Kuo[22]提出了一种非晶合金塑性变形理论,该理论基于在外加剪切应力的作用下,在自由体积区域启动的两种热激活剪切转变模式,预测了在低温下非常快速的剪切局部化.Falk 和Langer[40]在使用分子动力学模拟研究非晶合金变形行为时,将发生局部剪切重排的基本变形单元定义为剪切转变区,STZ 模型本质上是一个平均场模型,将局部流动缺陷的密度以及取向视为动态变量,并未对不同STZ 之间相关性进行描述[41],此外,塑性屈服过程中从堵塞到流动的转变受外加应力控制,应力低于屈服应力时,变形为纯弹性过程,当应力超过屈服应力时,STZ 被激活,同时发生屈服,然而一些实验表明,即使在室温下,非晶合金也会产生滞弹性或塑性变形[42,43].需要指出的是,Cavaille 等[23]基于高分子材料建立了一套完整理论,非晶固体存在纳米尺度上的密度起伏,其对应着熵和焓的变化,这些微观上的区域被定义为准点缺陷.该模型基于Palmer 等[44]提出的层级关联效应来确定原子迁移率、变形单元演化过程和宏观非弹性变形之间相关性,基于QPD,非晶合金微剪切畴(shear micro-domain,SMD)的形核、扩展以及湮灭等,既可以定量描述非晶合金原子或者分子移动性和黏弹性行为,还可以描述过冷液体的玻璃转变以及主弛豫(α relaxation)微观物理机制[45].本课题组先前工作中通过实验测量和理论预测的比较,在La60Ni15Al25非晶合金进行令人信服的验证[46].

非晶合金形成过程中,合金熔体冷却速率过快而导致原子来不及重排形成稳态的晶体,大量过剩自由体积或焓被冻结,从而使非晶合金处于一种亚稳状态.通过玻璃转变温度Tg以下的退火,可使非晶合金从亚稳态向更稳定能量状态迁移,玻璃转变温度以下退火导致非晶合金密度增加[47]、焓以及缺陷浓度降低[48,49],研究退火行为有利于建立非晶合金β 弛豫与微观结构非均匀性之间的联系.图5 为La62Cu12Ni12Al14非晶合金在退火温度373 K时,归一化储能模量E′/Eu,损耗模量E''/Eu和内耗随退火时间演化过程.可以发现随退火时间延长,储能模量逐渐增大,损耗模量和内耗随退火时间延长而逐渐降低.退火处理过程中内耗tanδ随退火时间演化过程可以用扩展指数(Kohlrausch-Williams-Watts,KWW)方程[50]描述:

图5 等温退火过程中归一化储能模量、损耗模量和内耗tanδ 随退火时间的演化 (退火温度为373 K)Fig.5.Evolution of the normalized storage modulus,loss modulus and internal friction with annealing time in annealing process (annealing temperature is 373 K).

其中A表示弛豫强度,τ表示特征弛豫时间,ta表示退火时间.由图5 可以看出,可知非晶合金内耗tanδ随退火时间增加而降低,βaging为KWW 扩展指数,与玻璃材料的结构非均匀性密切相关,取值介于0 与1 之间,βaging=1 时退火过程内耗演变((1)式)遵循单德拜弛豫时间对应指数衰减函数,βaging数值越小,偏离德拜弛豫程度越大,弛豫时间分布越广,动态非均匀性越大,本文中βaging=0.45,与其他典型非晶合金一致.根据QPD,可以预期弛豫和变形有关的原子重排首先在原子排布松散的准点缺陷处发生,从而使得非晶合金内部原子可以进行中短程原子协同运动,形成宏观上的弛豫行为,退火使得非晶合金缺陷浓度降低,原子移动性降低,玻璃体系向更稳定状态迁移.

图6 为铸态和退火态La62Cu12Ni12Al14非晶合金动态弛豫行为的对比分析,发现以铸态样品作为参考态,退火后非晶合金体系β 弛豫强度有所降低,此前有相关工作定量分析了不同退火时间对非晶合金β 弛豫强度的影响,并采用非对称双势阱(asymmetric double-well potential,ADWP)模型成功解释了弛豫时间τβ增大和损耗模量最大值减小之间的关联性[51].但由于本文选取模型体系并没有表现出明显分离的β 弛豫峰,α 弛豫和β 弛豫耦合,故只能定性表征β 弛豫强度降低程度,无法进行定量表征.前已述及,非晶合金β 弛豫联系着其微观结构非均匀性,非晶合金体系β 弛豫强度降低对应着其微观结构缺陷浓度降低.

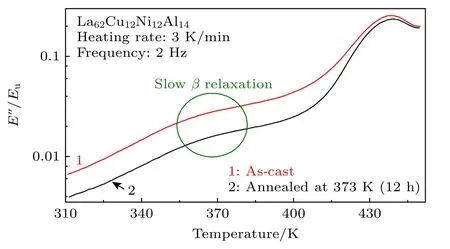
图6 铸态和退火态La62Cu12Ni12Al14 非晶合金的归一化损耗模量随温度的演化Fig.6.Temperature dependent normalized loss modulus in La62Cu12Ni12Al14 amorphous alloy at different states: ascast state and annealed state.

为了深入探究退火前后La62Cu12Ni12Al14非晶合金微观结构演变,对铸态以及退火态样品进行X 射线衍射,均表现为典型的玻璃宽泛的“馒头峰”,表明退火过程中样品并未晶化,如图7(a)所示.图7(b)为铸态以及退火态样品蠕变曲线,图中实线为KWW 方程拟合曲线,为直观表征退火时间对蠕变行为影响,移除加载后瞬时弹性变形,观察到随退火时间延长,La62Cu12Ni12Al14非晶合金特征弛豫时间τ和扩展指数β整体表现为上升趋势,τ由铸态约780 s 延长到退火态约1117 s,β由铸态约0.52 增加到退火态约0.56,表明退火处理导致非晶合金体系趋向更稳定状态,变形单元更难以被激活.

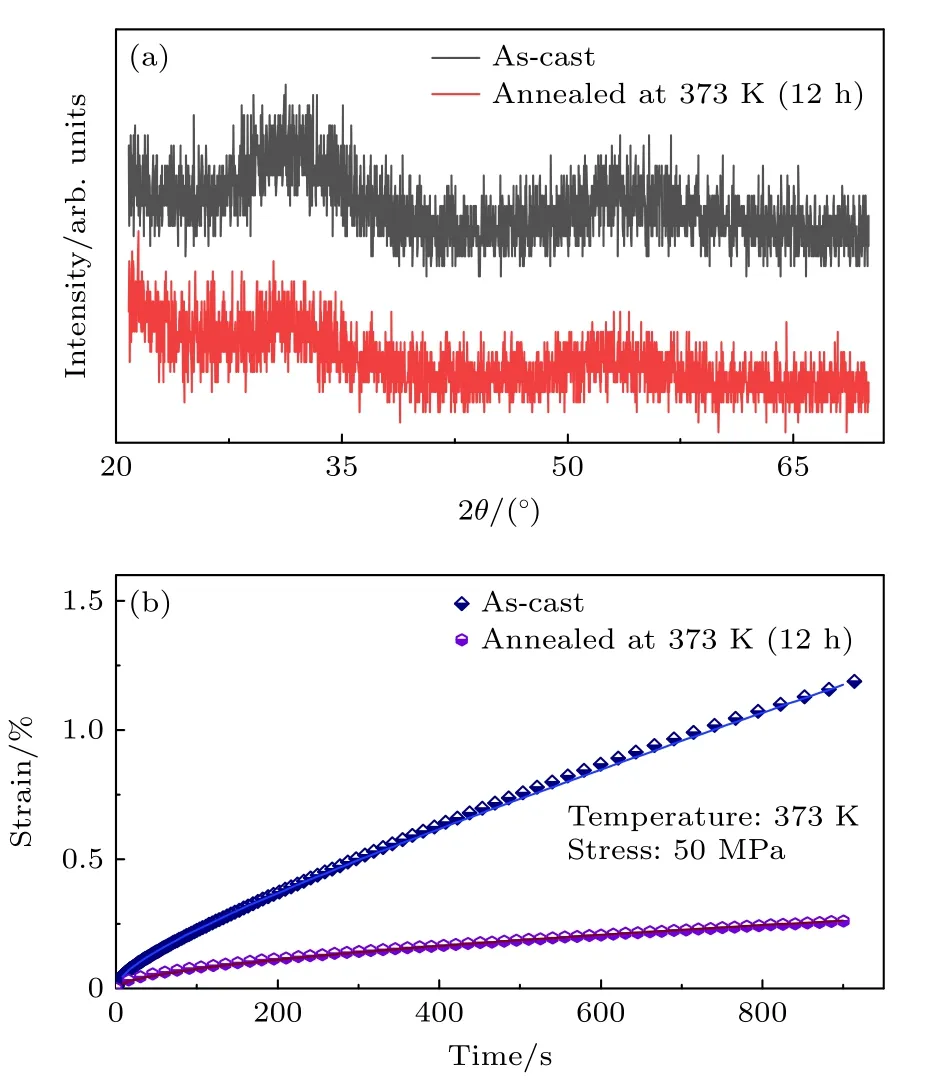
图7 (a) 铸态和退火态La62Cu12Ni12Al14 非晶合金XRD 衍射图;(b) 铸态和退火态La62Cu12Ni12Al14 非晶合金蠕变曲线.测试温度为390 K,施加应力为60 MPa,图中实线为KWW方程拟合曲线Fig.7.(a) XRD patterns of La62Cu12Ni12Al14 amorphous alloy with different states,as-cast state and annealed state;(b) creep deformation process of La62Cu12Ni12Al14 amorphous alloy with different states,as-cast state and annealed state.The measurement temperature is 373 K and the applied stress is 50 MPa,the solid lines denote KWW fitted curves.

基于QPD,非晶合金调节滞弹性变形的原子簇被称为微剪切畴,其代表几十甚至上百原子组成的原子团簇,微剪切畴内部可发生原子重排,外部边界具有弹性能.在外部应力场作用下,准点缺陷处首先发生原子运动,导致少数原子优先沿最大剪切面方向局域化运动形成微剪切畴.在外界应力场持续作用下,微剪切畴进一步生长扩展,随应力不断增大,相邻微剪切畴边界合并.微剪切畴形成和长大对应于滞弹性变形,应力卸载时微剪切畴收缩,滞弹性变形回复,相邻微剪切畴边界合并对应于塑性变形,其边界弹性能释放,变形不可逆.已有研究工作中[52,53],为了量化滞弹性和塑性变形分量的影响,分别考虑滞弹性变形和塑性变形的形变速率,滞弹性和塑性变形分量主要与初级弛豫(α 弛豫)有关,而β 弛豫与非晶合金中有限数量原子的局部运动有关,故也需考虑β 弛豫在非晶固体变形中的贡献.在此基础上加入弹性分量贡献,变形过程中总变形柔量表达式可写作[46]:

其中Aan,Avp,Aβ分别为相应滞弹性变形、塑性变形和β 弛豫过程强度,Eel为室温时材料的弹性模量,τmax为最大弛豫时间,τan,τβ为滞弹性变形及β 弛豫对应弛豫时间,χ为关联因子,用于衡量原子分级运动关联强弱程度,其数值介于0—1 之间,χ值越大代表体系原子/分子分级运动关联强弱程度越低.

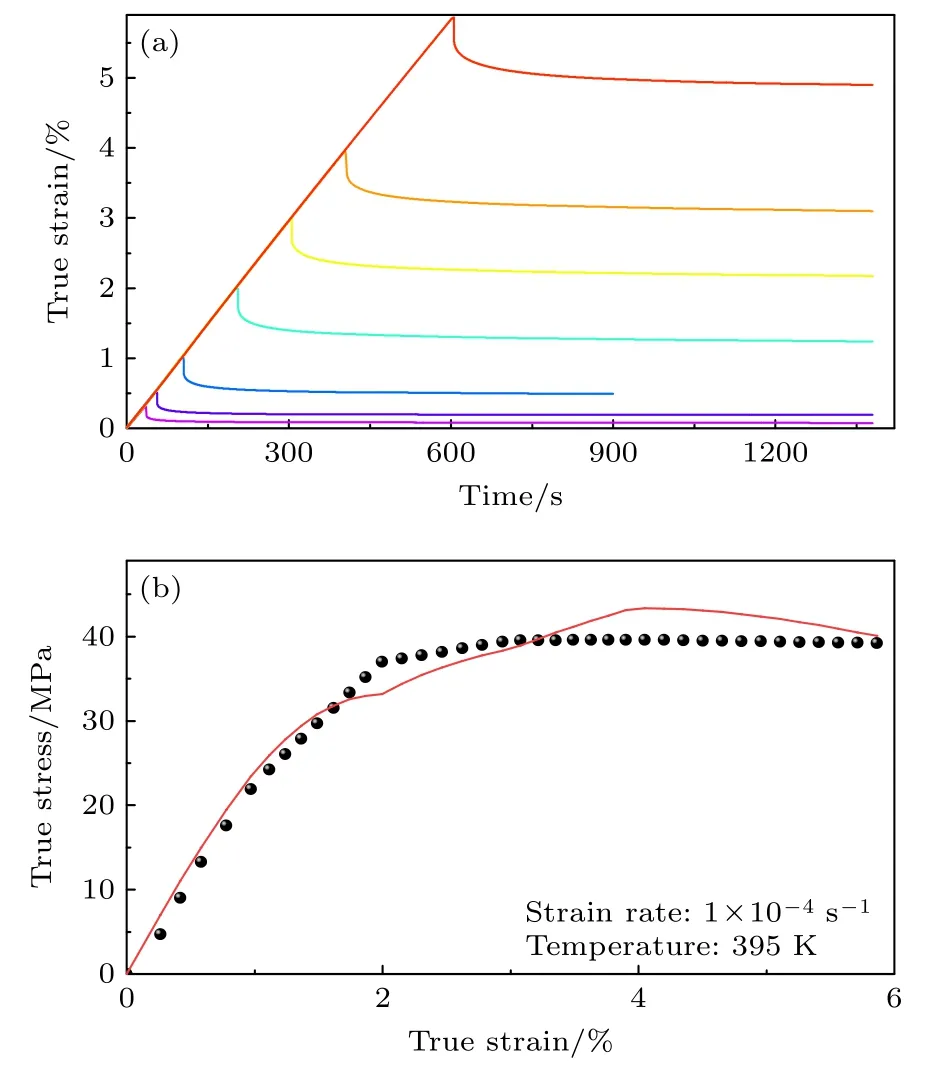
在上述计算过程中,还需考虑关联因子χ变化,该参数随体系无序度的升高而增大,因而也随缺陷浓度升高而增大.当温度高于玻璃转变温度Tg时,可以假设关联因子χ与玻璃体系缺陷浓度呈线性关联.另一方面,当非晶合金处于T

其中,ω是DMA 实验角频率,J∗(iω) 是复柔量.由于非晶合金微观结构非均匀性本质,不同准点缺陷特征时间、能量分布各异,β 弛豫不能采用单一的特征时间,QPD 中假定其遵循正态分布,即[53,54]

其中,B为分布宽度;〈τβ〉为τβi的最可几特征时间,即特征时间分布中所占权重最大的特征时间值;表示每个特征时间τβi的统计权重.考虑(4)式中的特征时间分布,并对(2)式和(3)式进行改写,最终可获得非晶固体的力学响应表达式:

(5a)式用于计算常规力学试验(拉伸实验)的应力应变曲线,可以解释常规力学试验(拉伸和蠕变)过程中的应力应变关系,(5b)式由(5a)式通过积分变换而来,用于描述周期应力下动态力学行为中的材料力学性能(模量)演化.本文进行了动态力学分析实验以及高温拉伸实验,研究不同力学激励下非晶合金的力学响应,尝试建立起动态弛豫机制与其宏观力学行为的潜在关联.图8 中实线为通过(5b)式拟合获得的动态力学分析实验储能模量和损耗模量演化关系,与实验结果对比表明,该模型可有效描述整个实验过程中的模量演化过程,包括α 弛豫、β 弛豫以及玻璃转变时储能模量E'的急剧下降,而在375—410 K 的温度范围内计算得到的曲线与实验数据有误差,可能是因为在Tg以下的温度范围内假设关联因子χ为常数,升温过程中虽然0.8Tg—Tg之间会随温度发生变化.然而其具体演化无法确定,要考虑不同温度下的平衡值以及老化过程影响,而且老化动力学随温度会发生变化.为了简化计算,此处在玻璃转变温度以下假定关联因子χ为定值,故而产生实验测量与理论计算之间的误差,采用此假设对计算结果影响有限,并不大幅度改变数据演化趋势.

图8 La62Cu12Ni12Al14 非晶合金储能模量和损耗模量随温度的演化,符号代表实验数据,实线代表 (5b) 式计算数据Fig.8.Evolution of the normalized storage modulus and loss modulus with temperature of La62Cu12Ni12Al14 amorphous alloy.Symbols represent the experimental data,solid line represents the calculated data of the Eq.(5b).

3.3 高温流变行为

非晶合金的变形行为对于温度十分敏感,通常较低温度非晶合金塑性变形一般为非均匀变形,表现为局域化剪切带形成与传播.随温度升高,变形局域化程度降低,剪切带更宽,边界更加弥散.在高温区域(T>0.8Tg)内,主要表现为均匀变形,非晶合金内部每个体积元对变形均产生贡献,整体参与流动变形.了解非晶合金高温变形过程中的结构响应,这不仅在成型中具有重要的应用价值,而且对于了解非晶合金非弹性变形的微观结构演化具有重要意义.

为了确定弹性、滞弹性和塑性变形分量的贡献以及各分量在变形过程中的演化规律,在一组单轴拉伸实验中将样品拉伸至不同应变,随后撤去应力回复,定义其中即时回复应变为弹性分量,缓慢回复应变为滞弹性分量,不可回复应变为塑性分量,如图9(a)所示.将变形分量代入(5a)式得到计算曲线,如图9(b)所示,模型基本吻合拉伸实验过程中应力应变关系,包括弹性及滞弹性阶段、屈服阶段以及稳态流变阶段.应当指出本文中χ随应变逐渐增大,最终趋于稳定,该演化过程是由于应力诱导产生缺陷和热湮灭之间的竞争.然而在非晶合金的宏观屈服过程中,可能包含更复杂的黏弹塑性转变和宏观缺陷(孔洞、缺口)效应,因此仍需进一步探究.

图9 (a)单轴拉伸回复实验过程中La62Cu12Ni12Al14 非晶合金的时间-真实应变曲线;(b)实验过程中La62Cu12Ni12Al14非晶合金的真实应力-真实应变曲线,符号为实验数据,曲线为(5a)式计算得到Fig.9.(a) True strain-tine curve of La62Cu12Ni12Al14 amorphous alloy in uniaxial tensile and recovery experiment;(b) true stress-true strain curve of La62Cu12Ni12Al14 amorphous alloy,symbols represent the experimental data,solid line represents the calculated data of Eq.(5a).

非晶合金是典型的黏弹性材料,研究非晶合金的率相关性有利于进一步了解非晶合金的变形机制.如图10 所示,在415 K 温度下进行了不同应变速率下的拉伸试验,在给定温度下,稳态流动应力随着应变速率的增大而增大.稳态流变现象对应材料内部准点缺陷浓度的动态平衡,即缺陷产生速率和缺陷湮灭速率相等.非晶合金稳态流变应力σflow,应变速率与名义黏度η满足η=σflow/,计算得到每个应变速率下的名义黏度.

图10 La62Cu12Ni12Al14 非晶合金在415 K 时应变率跳跃拉伸实验真实应力-真实应变曲线Fig.10.True stress-true strain curve of La62Cu12Ni12Al14 amorphous alloy by strain jump tensile experiment at 415 K.

图11 为不同温度下黏度随应变速率演化过程,可以看到黏度随温度升高或应变速率增大而减小.给定温度下,低应变速率时黏度基本与应变速率无关,不表现率相关性,表现为牛顿流变,在较高应变速率下随着应变速率的增加,黏度开始逐渐加速降低,发生从牛顿流变到非牛顿流变的转变.非晶合金黏度关于应变速率的演化可以通过KWW方程拟合[55]:

图11 La62Cu12Ni12Al14 非晶合金在不同温度时名义黏度η 随应变速率 的关系Fig.11.Correlation between the nominal viscosity η and the strain rate of La62Cu12Ni12Al14 amorphous alloy at different temperature.

式中,ηN表示牛顿黏度;σtc表示牛顿流变与非牛顿流变转变特征应力;βKWW为描述黏度的KWW扩展指数,表示高温流变偏离牛顿流变的程度,通常βKWW介于0 和1 之间,βKWW等于1 时为牛顿流变.数值越小高温流变偏离牛顿流变的程度更大.分析得到400 K,405 K,410 K 条件下KWW 扩展指数分别为0.84,0.63,0.60.βKWW随温度升高而降低,表明高温流变偏离牛顿流变的程度随温度升高而增大,即非牛顿流变区域表观黏度随应变速率增加下降速度变快.值得注意的是,在图5 退火实验中计算得到βaging=0.45,两处虽然均使用扩展指数方程形式以描述实验现象,然而其物理背景并不相同,前者退火实验本质为老化过程,是热激活条件的部分缺陷位点相当局域化的原子重排,后者是黏度外加应力条件测得黏度随应变速率变化过程,涉及热力耦合作用下原子大规模运动,故而数值并不相同.

为了更深入探究非晶合金高温变形行为,进一步了解非晶合金在常规拉伸实验条件下的力学响应.将不同温度条件下的名义黏度通过牛顿黏度进行归一化,选取405 K 作为参考温度,将其他温度下归一化数据平移至参考温度得到黏度主曲线,从而可以在更宽的应变速率范围内观察黏度的变化[56],该曲线理论上对于平衡态均适用,因此在玻璃转变温度Tg附近及以上均适用,在玻璃转变温度以下,只要应变速率足够低使得稳态流动应力可以进行测量,理论上也适用,因为在稳态流动阶段,体系亦处于当前外加刺激下的平衡状态,此时老化导致的有序与力致无序达到动态平衡.然而温度远低于玻璃转变温度时,非晶合金变形局域化通过剪切带断裂或者无法在实验中得到稳态流动阶段,因此无法通过该实验方法测量黏度.此外通过两种不同理论对黏度主曲线进行分析解释.如图12(a)所示,以上由牛顿流变到非牛顿流变的转变行为,可以通过扩展指数方程((6)式)很好描述,其中参数βKWW=0.68,与其他典型非晶合金体系结果一致,说明这些非晶合金具有相同的高温变形物理机制.

图12 采用扩展指数方程(a)和QPD 理论(b)描述La62Cu12 Ni12Al14 非晶合金归一化黏度主曲线 (参考温度为 405 K)Fig.12.Master curve of the normalized viscosity of La62Cu12 Ni12Al14 amorphous alloy was described by the KWW equation (a) and QPD theory (b) (reference temperature is 405 K).

扩展指数方程虽然可以准确描述高温流变过程中的黏度变化,但是扩展指数方程参量物理意义并不清晰,无法进一步了解这种转变的本质[57].接下来采用参量物理意义明确的QPD 来描述非晶合金高温变形行为.根据QPD,非晶合金在高温变形中由于变形产生缺陷数量同热驱动湮灭缺陷数量达到动态平衡,从而发生稳态流变行为.根据Perez 等[58]发展的分级关联理论,得到非晶合金黏度与应变速率之间关系[59]:

式中,σ0为材料在0 K 时的屈服极限,Uβ为β 弛豫激活能,η0表示应力为0 时的黏度,牛顿黏度ηN是低应变率下的黏度且低应变率一定范围内下保持不变,应变率趋向于0时,应力也趋向于0,故η0≈ηN.前已述及,基于现有的DMA 数据,La 基非晶合金β 弛豫激活能Uβ=1.11 eV,图12(b)中实线为借助QPD 预测的曲线,与实验得到的黏度主曲线吻合.基于QPD 的微剪切畴演化过程,运用动态力学分析试验得到的物理参数,成功描述了高温流变试验的应力-应变响应,建立了动态弛豫行为与宏观力学行为(比如蠕变)之间的关联,描述了非晶合金弛豫行为和高温拉伸过程中微观结构的力学响应.

4 结论

本文以La62Cu12Ni12Al14非晶合金为模型合金,借助于动态力学分析和高温拉伸实验,基于QPD研究了非晶合金动态弛豫行为和高温流变行为,主要结论如下.

1)动态力学分析实验中模型体系储能模量和损耗模量随温度的演化过程可以分为3 个阶段:低温段的弹性阶段;325 K 升高至400 K 段的β 弛豫阶段;高温段(过冷液相区附近)的α 弛豫阶段.La62Cu12Ni12Al14非晶合金β 弛豫激活能较大,这可能源于其较低的微观结构非均匀性.

2)低于玻璃转变温度Tg退火导致非晶合金微观缺陷浓度降低,玻璃体系向更稳定状态迁移.这一过程对应储能模量增大,损耗模量及内耗减小,β 弛豫强度降低,激活能增大,玻璃体系原子移动性降低.

3)借助QPD,通过对微剪切畴的形成和生长及相邻微剪切畴边界合并的描述,可以量化总变形过程中弹性变形、β 弛豫、滞弹性变形以及塑性变形的贡献,得到非晶合金在不同激励下的力学响应表达式,准确描述和解释动态力学弛豫行为及高温变形行为.通过上述实验验证,小应变线性黏弹性动态力学行为和大应变力学行为在QPD 中都可以得到准确描述,为探究非晶合金弛豫机制、宏观力学行为及其微观物理本源的联系提供了新思路.非晶合金作为一种典型非晶材料,本模型有望于扩展到其他非晶材料,有助于深入理解一般非晶材料的弛豫机制及变形行为.

4)非晶合金高温变形分为三阶段: 即弹性及滞弹性阶段、屈服阶段和稳态流动阶段.其高温变形受温度与应变速率的影响,名义黏度随应变率增大或温度升高而减小,在低应变率或高温情况下,随着应变率降低以及温度升高可能会发生非牛顿流变向牛顿流变转变行为.La62Cu12Ni12Al14非晶合金的高温流变行为不仅可以通过扩展指数方程描述,结合动态力学分析试验得到的物理参数,同样可以采用QPD 刻画其黏度主曲线,建立了动态力学弛豫行为与高温流变行为之间关联.同样,为进一步探究非晶合金变形行为的微观本源提供了数据积累.