椭圆函数背景下Gerdjikov-Ivanov方程的多呼吸子*
姚慧 张海强 熊玮玥
(上海理工大学理学院,上海 200093)
作为非线性发展方程的一种特殊局域解,呼吸子具有包络振荡结构,且这种振荡呈现周期性变化.根据呼吸子在分布方向和演化方向的周期性,呼吸子主要有3 种类型,即Kuznetsov-Ma 呼吸子(Kuznetsov-Ma breather,KMB)、Akhmediev 呼吸子(Akhmediev breather,AB)和一般呼吸子(general breather,GB).近年来,周期背景下的呼吸子现象在许多非线性物理领域被观察到,比如在非线性光纤光学、流体力学等.研究表明背景周期波的调制不稳定性可以激发呼吸子的产生,且周期背景下的呼吸子具有非常丰富的物理性质和相互作用.因此,最近在周期背景下呼吸子的时空结构和相互作用引起了广泛关注.Gerdjikov-Ivanov 方程可以被用来描述在量子场理论、弱非线性色散水波、非线性光学等领域中的非线性物理现象.构造该模型的各种类型的解是非常有意义的工作.据了解,在椭圆函数背景下的多呼吸子之前还未被研究过.本文首先利用修正的平方波(modified squared wave,MSW) 函数法和行波变换法获得该方程的椭圆函数解.然后,在椭圆函数解初始条件下得到该方程Lax 对的通解.基于椭圆函数的转换公式以及积分公式,将势函数周期解化简为只含有Weierstrass 椭圆函数.然后,利用达布变换构造出在椭圆函数背景下呼吸子的具体表达形式.在椭圆函数背景下,推导出3 种不同类型的呼吸子,包括GB,KMB 和AB.最后,给出3 种呼吸子的时空结构三维图,并且展示它们之间相互作用的过程.
1 引言
随着自然科学的不断发展进步,研究非线性科学逐渐成为热点课题之一[1,2].在研究人员的不断探索下,人们发现非线性发展方程可以描述许多非线性现象,包括非线性薛定谔(nonlinear Schrödinger,NLS)方程[3,4],modified Korteweg-de Vrie(mKdV)方程[5],Hirota 方程和Gerdjikov-Ivanov(GI)方程[6]等.作为非线性发展方程的局域解,孤子、呼吸子和怪波可以被用来揭示自然科学和工程技术中的许多非线性局域现象.呼吸子泛指一类具有周期分布结构的非线性波,可以在有限背景的某一空间或传播方向局域,且具有周期振荡的特点[7].20 世纪70 年代,Kuznetsov[8]和Ma[9]对NLS 方程进行求解时发现了一种特殊的非线性波,该波表现出在空间方向上局域,时间方向上周期呼吸的特征.人们称为“Kuznetsov-Ma 呼吸子”(Kuznetsov-Ma breather,KMB) .
1986年,Akhmediev 等[10]在构造NLS 方程的呼吸子时,发现一类与KMB 的结构完全不同的非线性波,将其称为“Akhmediev 呼吸子” (Akhmediev breather,AB),该非线性波具有在时间方向上局域、空间方向上周期的特点.1988年,其以NLS 方程为研究对象,得到了一类不拘泥于时间或空间方向周期震荡的呼吸子[11].在学者们的不断探索下,呼吸子的应用价值已在非线性光学[12]、流体力学[13]、玻色-爱因斯坦凝聚和流体力学[14,15]等非线性物理中体现.NLS 方程一直以来都是孤子方程中的热点,于是在NLS 方程的基础上,开始寻找推广的NLS 方程.作为NLS 方程的可积推广,导数型NLS 方程[16]应运而生,该类型方程具有3 种不同形式,可以被用于描述非线性光学和其他领域中重要的非线性波的传播.1978年,Kaup 和Newell[17]提出了第一型导数NLS 方程:
1979年,Chen,Lee 和Liu[18]推导了第二型导数NLS 方程:
该方程被称作Chen-Lee-Liu (CLL)方程.自这两种模型建立以来,许多可积性质和精确解已经被大量的文献研究.Liu 等[19]发现CLL 模型的AB 呼吸子能够描述更一般的非对称调制不稳定性,并且给出了其精确解析谱.
1983年,Gerdzhikov 和Ivanov[20]提出了第三型导数NLS 方程:
即GI 方程.这里q=q(x,t),其中x表示空间坐标,t表示时间坐标,符号*表示复共轭,下标表示偏导数.已经有许多学者对此方程进行了研究,并推导出在零背景下的呼吸子[21–23].对于此方程,Fan[24,25]给出了双哈密顿结构、Liouvill 可积性和代数几何解.随后,Xu 等[26,27]构造了方程的髙阶怪波和高阶有理解的行列式表达式.
呼吸子在周期性背景上的动态行为比它们在恒定背景下的行为更真实[28].这样,椭圆函数周期背景下的解的研究尤为重要.Chen 和Pelinovsky[29]将Lax 对非线性化与达布变换方法相结合,提出了椭圆函数背景下NLS 方程多呼吸子的系统构造方法.利用此方法来求解许多非线性方程的呼吸子解,包括GB,KMB 和AB.由于GI 方程的Lax对谱问题不同于NLS 方程,在椭圆函数背景下构造这些解是一项非常困难的任务.除了标量系统中的呼吸子外,耦合系统(例如Manakov 系统)中的呼吸子也引起了广泛关注[30–33].研究表明耦合系统可以激发出新的矢量非线性现象[34]、非退化孤子[35]和非退化怪波[36].
本文主要研究椭圆函数背景下多呼吸子的非线性动力学.将从以下3 个方面对方程(3)进行研究: 1) 利用MSW 函数法和行波变换法获得该方程的椭圆函数解和Lax 对通解;2) 利用达布变换构造出在椭圆函数背景下呼吸子的具体表达形式,包括GB,KMB 和AB;3) 分析3 种呼吸子的时空结构分布、非线性动力学行为和相互作用.
2 Lax 对
GI 方程是完全可积的,它可以表示为一个线性系统的相容条件,即
这里,Ψ=(Ψ1,Ψ2)T是本征函数,λ是谱参数.由相容条件Ψtx=Ψxt或零曲率方程Ut-Vx+[U,V]=0可以推导出方程(3).
3 椭圆函数解和Lax 对通解
3.1 椭圆函数解
方程(3)有如下形式的解:
其中v(x,t) 是一个实函数,下文将对上述待定的势函数中的未知元素进行求解.
设定Ψ1=(ϕ1,φ1)T以及Ψ2=(ϕ2,φ2)T,建立平方波函数:
f,g,h满足以下线性系统:
由于矩阵U,V迹为零,很容易验证P(λ)=f2-gh不依赖于变量x,t,所以它只依赖于谱参数λ.研究表明可积演化方程的周期解或拟周期解与几何代数理论中的黎曼曲面概念有着一定的联系.为了得到方程(3)在初解(5)式周期背景上的呼吸子解,将P(λ) 设置为关于λ的一个多项式:
其中λj,j=a,b,c,d为多项式的根.
线性系统(6)和系统(7)具有多项式形式的解,故将f,g以及h写成如下形式:
比较等式P(λ)=f2-gh两边λ的系数,得到如下等式:
令|q|2=v,则(11)式转化为
根据韦达定理,得到ω关于v的表达式:
其中,R(v)是v的四次多项式:
结合方程组(6)和(7)以及方程(8)求导的结果,对比λ各阶系数的关系可以得到:
根据方程(17)和方程(18)可以得到v仅和δ=x+s1t有关,即:
显然,方程(19)具有椭圆函数解.这样,如果v已知,那么通过方程(5)就能求出q(x,t) .
结合方程组(6),(7)以及方程(9)求导的结果,对比λ各阶系数的关系可以得到:
当λ2=ω时,f(ω1/2)=,则(20)式可以转换为
因此可得到ω关于x和t的等式.由方程(21)和方程(22),易知ω仅依赖于相位δ=x+s1t.于是,GI 方程周期解的非线性相速度为
根据上述公式,得到q关于x,t的等式如下:
经行波变换后,周期解有如下形式:
将(13)式代入上式,则
显然,选取合适的λj应该满足v在两个正值之间振荡.若只有两个vi是正实数,则设置相应的λj使其在v1,v2之间振荡,且v1≥v2.若所有vi都是正实数,则我们设置相应的λj使v1≥v2≥v3≥v4.此时,变量v可以在v1,v2或者v3,v4之间振荡,且R(v)≤0 .
为满足以上条件,设λj由两对复共轭对组成:
由(15)式可得:
此时(16)式得到的vi均为复数值.
为寻找周期解,讨论变量v在区间v1≥v≥v2振荡,且v3,v4为实数的情况.选择初始条件δ=0时v=v1,(19)式具有如下形式的解:
3.2 Lax 对通解
对上述表达式进行化简,得到如下形式:
其中,A1和A2表示待定的复常数:
利用Lax 对中t部分的等式,可以求出φ1,t/φ1,ϕ1,t/ϕ,代入3.1 节所求的参数,得到
根据前面的定义,有
不失一般性,可设定A1=1,A2=-1.
同理,易得Lax 对的第2 组通解形式如下:
因此,给定椭圆函数势(23)的Lax 对的通解可以表示为
其中θ1,θ2由(29)式可知.
4 周期背景下的多呼吸子
4.1 解的化简
根据公式:
(1)根据国内外砂土液化资料分析研究结果表明,人工沉积的尾矿砂与天然沉积的砂土一样,地震时都可能发生液化,影响砂土液化的主要因素是相同的,液化机理也是一致的。因此可以利用判别天然砂土液化的方法来判别尾矿砂。
将(33)式代入(24)式中,可得
4.2 GI 方程的n 次达布变换
在规范变换下:
谱问题(4)式转换为
其中,U[1]和V[1]与Lax 对中的U和V的形式相同,不同的是q变为q[1] .
设Ψi=(ϕi,φi)T,i=1,2,···,n,为谱问题(4)式的n组线性无关的解,则n阶达布变换中新的解q[n]和初解q[0] 之间满足:
4.3 dn 椭圆函数背景下的呼吸子
单呼吸子的具体表达式为
其中,q,Ψ1,Ψ2,Ψ3和Ψ4分别为
式中,Ψi,i=1,2,3,4为谱参数λ取不同值时的线性解.因此,谱参数的值影响呼吸子解及其动态行为.通过改变谱参数的值,得到3 种呼吸子解,即GB,AB 和KMB.
选取特定参数,呈现出dn 背景下的呼吸子解λa=1+0.5i,λb=1-0.5i,λc=0.5+i,λd=0.5-i.
取参数λ1=0.3+1.1i,λ2=0.3-1.1i 则得到在dn 背景下的一个AB (图1).观察可得,此呼吸子的所有峰值都在t=0 这一条线上,此时这种呼吸子的振幅在原点处达到最大值为7.65.选取参数λ1=2+2i,λ2=2-2i,则获得了dn 背景下的一个KMB (图2).明显看出这种呼吸子是时间呼吸和空间局域的.此时,这种呼吸子在原点处的振幅达到最大值为10.95.选取参数λ1=0.3+1.3i,λ2=0.3-1.3i,获得了dn 背景下的GB(图3).此时,这种呼吸子在原点处振幅达到最大值为8.18.
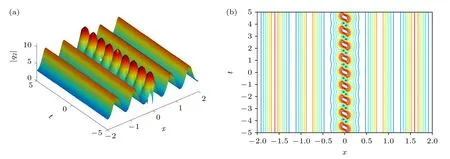
图2 dn-周期波背景上的KMBFig.2.KMB on the dn-periodic wave background.

图3 dn-周期波背景上的GBFig.3.GB on the dn-periodic wave background.
为了得到dn 背景下的双呼吸子,令n=4,根据(40)式,得到二阶呼吸子:
其中,Ψj(j=1,2,···,8) 有如下表达形式:
取参数λ1=2+2i,λ2=2-2i,λ3=0.5+2i,λ4=0.5-2i,则得到GB 和KMB 相互作用的时空结构(图4).可以观察到,两个呼吸子在相互作用后没有波峰的偏移,最大值为17.75.取参数λ1=2+2i,λ2=2-2i,λ3=0.1+1.8i,λ4=0.1-1.8i,得到AB 和KMB 相互作用的时空结构(图5).选取参数λ1=1.5+1.6i,λ2=1.5-1.6i,λ3=0.1+1.8i,λ4=0.1-1.8i,得到AB 和GB 相互作用的时空结构(图6).

图4 dn-周期波背景上的GB 和KMB 相互作用Fig.4.Interaction between GB and KMB on the dn-periodic wave background.
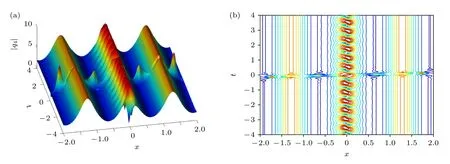
图5 dn-周期波背景上的AB 和KMB 相互作用Fig.5.Interaction between AB and KMB on the dn-periodic wave background.
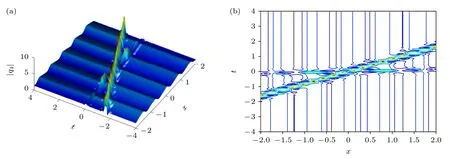
图6 dn-周期波背景上的AB 和GB 相互作用Fig.6.Interaction between AB and GB on the dn-periodic wave background.
4.4 一般椭圆函数背景下的呼吸子
与dn 背景下的呼吸子类似,在一般椭圆函数背景下构造3 种呼吸子,即GB,AB 和KMB.设定合适的参数来固定背景波λa=0.5+0.3i,λb=0.5-0.3i,λc=1+0.9i,λd=1-0.9i.取谱参数λ1=0.5+1.5i,λ2=0.5-1.5i,则得到一般椭圆函数背景下的一个AB(图7).此呼吸子的峰值 为8.69.选取参数λ1=1.8+1.8i,λ2=1.8-1.8i,得到了一般椭圆函数背景下的一个KMB(图8),此时最大值为8.28.取谱参数λ1=2+2i,λ2=2-2i,得到一般椭圆函数背景下的GB(图9),此时最大值为8.18.
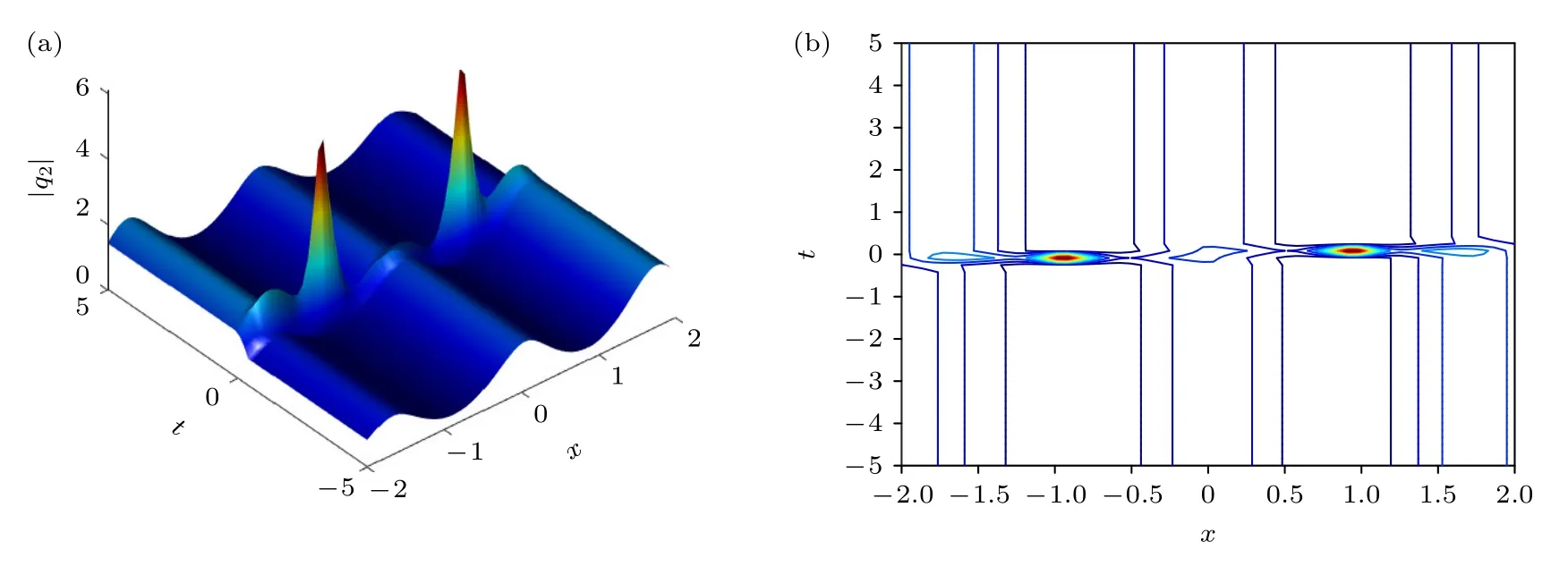
图7 一般周期波背景上的ABFig.7.AB on the general periodic wave background.

图8 一般周期波背景上的KMBFig.8.KMB on the general periodic wave background.

图9 一般周期波背景上的GBFig.9.GB on the general periodic wavebackground.
与dn 背景下构造二呼吸子相同,根据(44)式,选取合适的参数得到一般椭圆函数背景下的双呼吸子.取参数λ1=2+2i,λ2=2-2i,λ3=0.5+2i,λ4=0.5-2i,得到了GB 和GB 相互作用的时空结构(图10).可以看出,两个呼吸子在相互作用后没有波峰的偏移,最大值为13.27.取参数λ1=2+2i,λ2=2-2i,λ3=0.1+2i,λ4=0.1-2i,则得到了GB 和KMB 相互作用的时空结构(图11),最大值为16.94.取参数λ1=0.2+i,λ2=0.2-i,λ3=1.4+1.4i,λ4=1.4-1.4i,则得到AB 和GB相互作用的时空结构(图12),波峰的最大值为10.05.

图11 一般周期波背景上的KMB 和GB 相互作用Fig.11.Inacteraction between KMB and GB on the general periodic wave background.

图12 一般周期波背景上的AB 和GB 相互作用Fig.12.Interaction between AB and GB on the general periodic wave background.
5 结论
本文系统地构造了椭圆函数背景下GI 方程的多呼吸子.借助MSW 方法和行波变换,导出了椭圆函数解和Lax 对通解.在椭圆函数背景下,推导出3 种不同类型的呼吸子,包括GB,KMB 和AB.最后,给出了3 种呼吸子的时空结构三维图,并且展示它们之间相互作用的过程.希望本文获得的结果将有助于理解在流体动力学、非线性光学等领域中周期背景下的呼吸子动力学行为和相互作用.

