Robust Space-Time Adaptive Track-Before-Detect Algorithm Based on Persymmetry and Symmetric Spectrum

Xiaojing Su, Da Xu, Dongsheng Zhu, Zhixun Ma

Abstract: Underwater monopulse space-time adaptive track-before-detect method, which combines space-time adaptive detector (STAD) and the track-before-detect algorithm based on dynamic programming (DP-TBD), denoted as STAD-DP-TBD, can effectively detect low-speed weak targets.However, due to the complexity and variability of the underwater environment, it is difficult to obtain sufficient secondary data, resulting in a serious decline in the detection and tracking performance，and leading to poor robustness of the algorithm.In this paper, based on the adaptive matched filter (AMF) test and the RAO test, underwater monopulse AMF-DP-TBD algorithm and RAO-DP-TBD algorithm which incorporate persymmetry and symmetric spectrum, denoted as PSAMF-DP-TBD and PS-RAO-DP-TBD, are proposed and compared with the AMF-DP-TBD algorithm and RAO-DP-TBD algorithm based on persymmetry array, denoted as P-AMF-DP-TBD and P-RAO-DP-TBD.The simulation results show that the four methods can work normally with sufficient secondary data and slightly insufficient secondary data, but when the secondary data is severely insufficient, the P-AMF-DP-TBD and P-RAO-DP-TBD algorithms has failed while the PSAMF-DP-TBD and PS-RAO-DP-TBD algorithms still have good detection and tracking capabilities.

Keywords: space-time adaptive detection; track before detect; robustness; persymmetric property;symmetric spectrum; AMF test; RAO test

1 Introduction

In the complex hydrological environment of shallow water, reverberation seriously affects the detection performance of the active sonar.Especially when the sonar carrier has a certain velocity, the reverberation received from different directions has different Doppler frequency shifts,resulting in a large expansion of its power spectrum in the space-time two-dimensional plane,showing the characteristics of space-time coupling [1-3].With the miniaturization, low-speed and better acoustic concealment of underwater targets such as unmanned vehicles and submarines, the target echo signal is very weak.As a result, low-speed weak targets are submerged in the reverberation and unable to be effectively detected with single frame data.

In order to solve the problem mentioned above, an underwater monopulse space-time adaptive track-before-detect method [4], which uses the decision statistic of underwater monopulse space-time adaptive detection (STAD) [5]as the value function of the track-before-detect method based on dynamic programming (DPTBD) [6,7], denoted as STAD-DP-TBD, is proposed.This method effectively combines the STAD and the DP-TBD, and improves the output signal-to-reverberation ratio by suppressing reverberation and multi-frame accumulation, so as to realize effective detection and tracking of low-speed weak targets.Although the underwater monopulse STAD-DP-TBD model suitable for motion sonar in shadow water has been constructed [4], there are still several problems to be solved, especially the poor robustness of the algorithm due to insufficient secondary data.Due to the complex and variable underwater environment, the motion sonar often works in the nonhomogeneous reverberation environments, making it difficult to obtain sufficient independent and identically distributed secondary data.According to the RMB criterion [8], the number of secondary data can not be less than twice of the space-time dimension of the system in order to ensure that the detection loss of the algorithm does not exceed 3 dB.

Insufficient secondary data can lead to inaccurate estimation of the covariance matrix,thereby affecting the accuracy of the algorithm.There are two important kinds of a priori information on the reverberation which can be incorporated in solving the detection problem in sample-starved scenarios.One is the persymmetric structure [9-11] of the reverberation covariance matrix due to the array geometry and the other is that the power spectral density (PSD) of the reverberation has a symmetric property with respect to zero-Doppler frequency [12,13].The two kinds of a priori information can yield structures that involve less unknown parameters to characterize the unknown covariance matrix so as to obtain an enhanced estimate [11].The STAD-DP-TBD method based on persymmetry array [14] can improve the robustness of the algorithm, and has better detection and tracking performances when the secondary is slightly insufficient.However, there is still a problem of poor robustness when the secondary data is severely insufficient.In order to further improve the robustness of the algorithm, this paper combines the two kinds of a prior information to propose a robust space-time adaptive track-before-detect algorithm suitable for active sonar.

2 Underwater Monopulse STADDP-TBD Algorithm

Assume that the array in sonar system is a linear array ofNidentical and uniformly distributed sensors.The number of range cells isL,and the sampling points in each range cell isM.The sonar system emits monopulse signal once to obtain (MN×L)-dimensional space-time data,which is called one frame data.It emits monopulse signalKtimes, that is, it scans the detection areaKtimes to obtainKframes echo data.When thel-th range cell is scanned at thek-th time, theMNsampled data can be obtained,which form an observation vector zlk.H0andH1are referred to as null hypothesis and alternative hypothesis, respectively.Then the detection problem of point-like target can be described as

where

1)nlk～CN(0,Rk) follows a complex circularly symmetric Gaussian distribution with zero mean and a covariance matrix ofRk.

2)αkis the amplitude of the target during thek-th scan.

3)lkis the range cell where the target exists during thek-th scan.

4)v(vdk,vsk)=stk(vdk)⊗ssk(vsk) is the spacetime steering vector, wherestk(vdk) is the spatial steering vector, andssk(vsk) is time-domain steering vector.

5) The reverberation covariance matrix for each scan is invariant in the homogeneous environment, that isR1=···=RK.

STAD uses the AMF and the RAO respectively, and the decision statistics of the two detectors respectively are taken as the value function of DP-TBD, then the AMF-DP-TBD algorithm and the RAO-DP-TBD algorithm are obtained.

The decision criterion of the AMF-DP-TBD in the homogeneous environment [4] is

whereDrepresents the range-doppler position where the target is present in the range-Doppler plane,v(vk) represents the space-time steering vector of thek-th scan,zlk,krepresents the observation vector of the range celllkwith the target during thek-th scan,ηAMF-DP-TBDrepresents the decision threshold of the AMF-DP-TBD.

When signal-to-reverberation ratio is low,Rˆ can be approximated as

wherezl,krepresents the observation vector of thel-th range cell during thek-th scan.

The decision criterion of the RAO-DP-TBD in the homogeneous environment [4] is

Use (2) and (4) as the value function of the DP-TBD algorithm for dynamic programming iteration.At thek-th scan( 2 ≤k≤K), find and record the state that can maximize the value function in all possible statesxk-1that may transit to the statexk.Compare the final cumulative maximum value function with the threshold to get the target detection result, and then use the maximum value function of the last frame to achieve trajectory backtracking and estimate the target trajectory.

The evaluating indicators of the STAD-DPTBD algorithm [4] include the detection probabilityPdand the accurate tracking probabilityPdt.Pdis the probability that the maximum cumulative value function exceeds the detection threshold when the target exists.AndPdtrefers to the probability that the error between the estimated target trajectory and the actual target trajectory in each frame is within the allowable error range when the target is detected.Here, the accurate tracking means that the estimated target trajectory and the actual target trajectory in each frame are in the same range cell, that is, the allowed error range is zero.

3 STAD-DP-TBD Algorithm Based on Persymmetry and Symmetric Spectrum

3.1 Problem Modeling

One frame data in Eq.(1) is taken in order to facilitate the analysis of the problem, then the binary hypothesis testing problem can be written as the following form

wherezis the data under test(primary data),andzlis the secondary data.αis an unknown signal amplitude which is modeled as a deterministic factor, andvis the target space-time steering vector.nandnlare independent and identically distributed circularly symmetric complex Gaussian reverberation vectors with zero mean and covariance matrixR.

3.2 Persymmetric Structure

For an active system utilizing symmetrically spaced linear array for spatial domain processing,or symmetrically spaced pulse train for temporal domain processing, the resultant covariance matrix and the steering vector have the persymmetric property: it is conjugate symmetric about the main diagonal and symmetric about the secondary diagonal.zandzlare conjugate symmetric vectors, then construct new vectors as below

whereza,zb,zalandzblare independent and identically distributed circularly symmetric complex Gaussian vectors.(·)*denotes complex conjugate operation.J ∈RMN×MNis aMN-dimensional permutation matrix where the entries of the main cross-diagonal are one and the remaining entries are zero, written as the following form

Then

Perform the covariance matrix estimate using the secondary data

where (·)Hdenotes complex conjugate transpose operation.

As a consequence, we can recase problem(5) into the equivalent form

wherena=(n+Jn*)/2,nb=(n-Jn*)/2,nal=(nl+Jnl*)/2,nbl=(nl-Jnl*)/2,αr=Re{α},αi=Im{α}, Re(·) denotes the operation of taking the real part, and Im(·) takes the imaginary part.

Observe that the number of secondary data is twice that in problem (5).

3.3 Spectral Symmetric Property

Further considering the spectral symmetric property, it can be concluded from [12,13] that the PSD of the reverberation has a symmetric property with respect to zero-Doppler frequency, so the covariance matrix is real-valued which implies that the real and imaginary parts ofna,nb,nalandnblare statistically independent and identically distributed real Gaussian vectors.The received data is modeled by using circular symmetric complex Gaussian vectors

wherezar,zai,zbr,zbi,zalr,zali,zblrandzbliare independent and identically distributed real Gaussian vectors, and

Combing the persymmetric property, it is obtained that

Estimate the reverberation covariance matrix

Thus, problem (13) is equivalent to

Notice that the number of secondary data in problem (18) is four times the number of secondary data in problem (5).

3.4 Detector Designs

First, define as follows

1) DefineZas the primary data matrix,

2)Z0is the secondary data

Z0=[Z10,Z20]∈RMN×4(L-1), where

3)Vis space-time steering vector

4)θris the parameter vector of estimated target

5)θsis nuisance parameter vector

=[1,pT(Q)]∈R((MN-1)MN/2+1)×1, wherep(Q)is a vector-valued function that selected in unequivocal way the elements of a symmetric matrixQ.

6)θis the entire parameter vector

Under the above definition, the joint probability density function ofZandZ0under H1is

where

The joint probability density function ofZandZ0under H0is

where

3.4.1 AMF-DP-TBD Based on Persymmetry and Symmetric Spectrum

For the problem (18), the AMF-DP-TBD method using persymmetric and spectral symmetric property is proposed based on the AMF test in the homogeneous reverberation background, denoted as PS-AMF-DP-TBD.

The AMF detection criterion for knownQin a homogeneous background [4] is

Take the logarithm of equation (24), and get

where

Set to zero the gradient of (26) with respect toαrandαi, then obtain

Substitute Eqs.(27) and (28) into (25),and replaceQwithS, then get the decision statistic of the AMF based on persymmetric and symmetric spectrum, noted as PS-AMF

Then obtain the value function of the PSAMF-DP-TBD

whereVkrepresents the space-time steering vector being transformed into the real domain during thek-th scan,Skrepresents the sample covariance matrix based on secondary data during thek-th scan, Tr(·) denotes the trace of a matrix, andηPS-RAO-DP-TBDrepresents the decision threshold of the PS-AMF-DP-TBD.

3.4.2 RAO-DP-TBD Based on Persymmetry and Symmetric Spectrum

For the problem (18), the RAO-DP-TBD method using persymmetric and spectral symmetric property is proposed based on the RAO test in the homogeneous reverberation background, denoted as PS-RAO-DP-TBD.The RAO detection criterion [15] is

trum，noted as PS-RAO, andJ(θ)=J(θr,θs) is Fisher information matrix, denoted as

Then get

whereI2represents 2×2-dimensional identity matrix.

Then get the decision statistic of PS-RAO

The maximum likelihood estimate of the sample covariance matrix under H0is

Then obtain the value function of the PSRAO-DP-TBD

whereRˆ0krepresents the sample covariance matrix based on primary data and secondary data during thek-th scan, andηPS-RAO-DP-TBDrepresents the decision threshold of the PS-RAO-DPTBD.

The workflow of the above schemes is summarized as Tab.1.

4 Simulation Test

In this section, the performance of the proposed methods under the conditions of sufficient secondary data (the number of secondary data is twice that of the space-time dimension, that isL=2MN+1), slightly insufficient secondary data (the number of secondary data is consistent with the space-time dimension, that isL=MN+1) and severely insufficient secondarydata (the number of secondary data is one less than half of the space-time dimension, that is,L=MN/2), are discussed respectively and compared with the AMF-DP-TBD method based on persymmetry array(denoted as P-AMF-DPTBD), as well as the RAO-DP-TBD method based on persymmetry array (denoted as PRAO-DP-TBD).Simulation parameters:N=5,M=20,MN=100 , andK=6.

Tab.1 Workflow of proposed algorithm

Fig.1 and Fig.2 respectively show the comparison of the detection probability and the accurate tracking probability of the PS-AMF-DPTBD、 PS-RAO-DP-TBD、 P-AMF-DP-TBD and P-RAO-DP-TBD algorithms when the secondary data is sufficient(L=2MN+1).Fig.3 and Fig.4 respectively show the comparison when the secondary data is slightly insufficient(L=MN+1), while Fig.5 and Fig.6 respectively show the comparison in case of severely insufficient secondary data(L=MN/2).

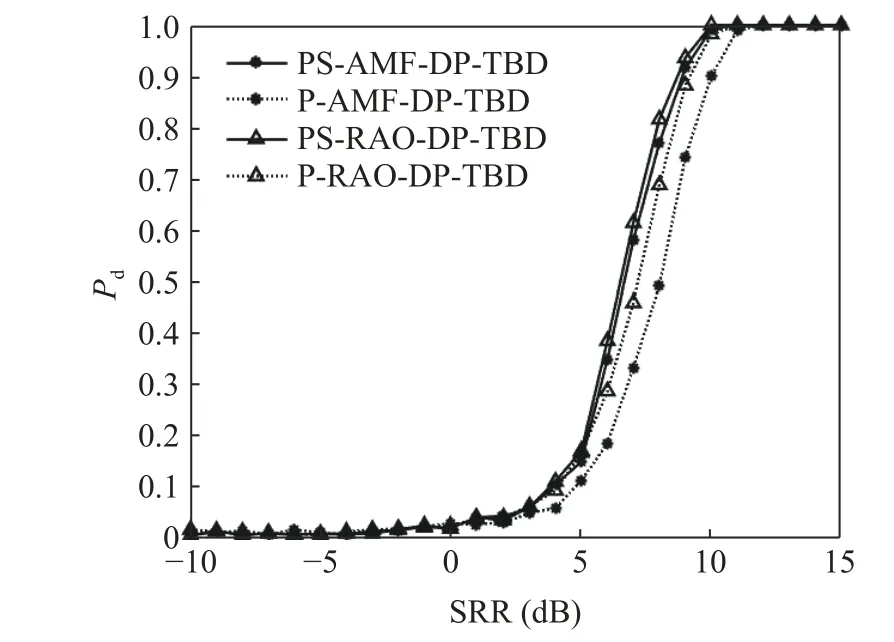
Fig.1 Detection probability when L=2MN +1

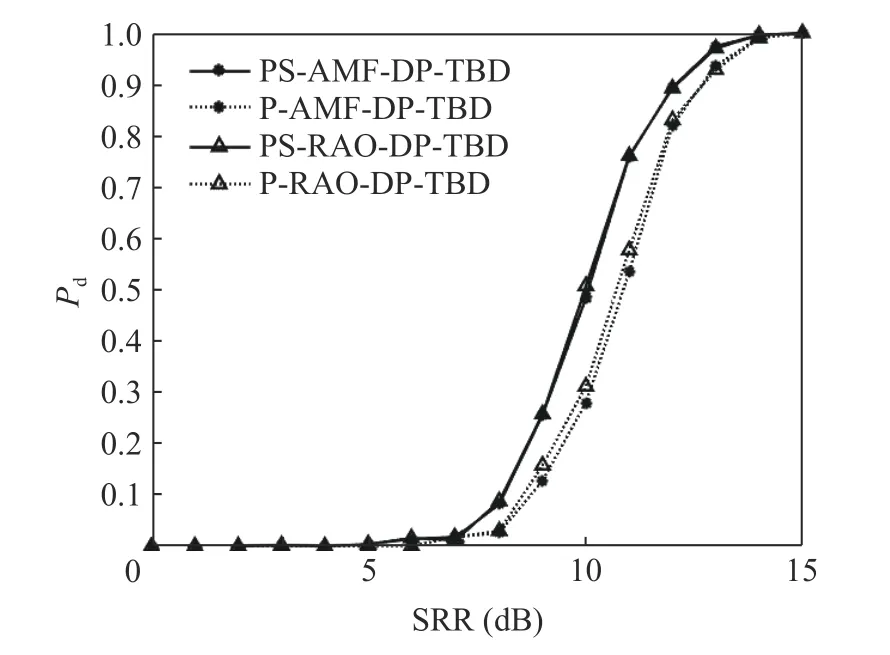
Fig.2 Accurate tracking probability when L=2MN +1

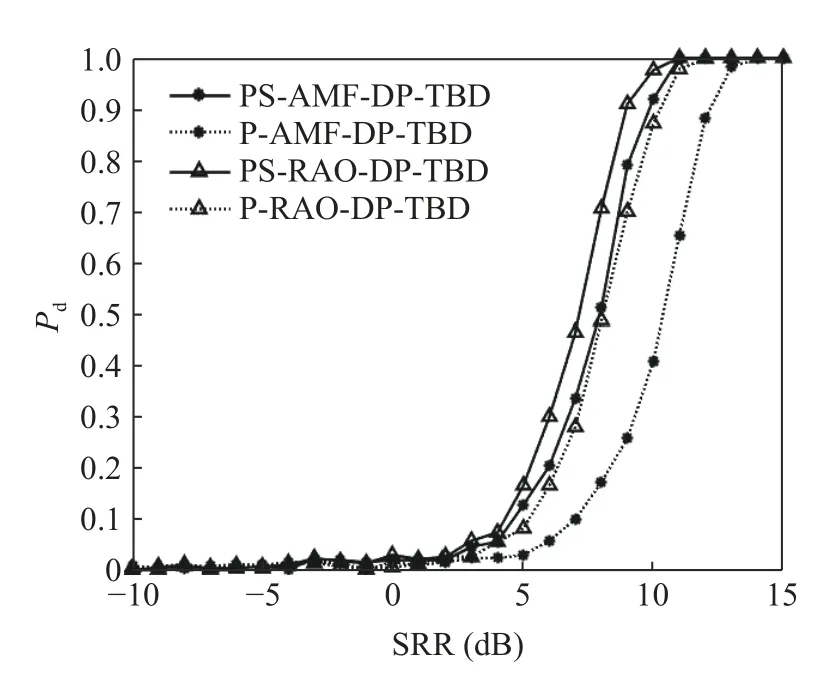
Fig.3 Detection probability when L=MN +1

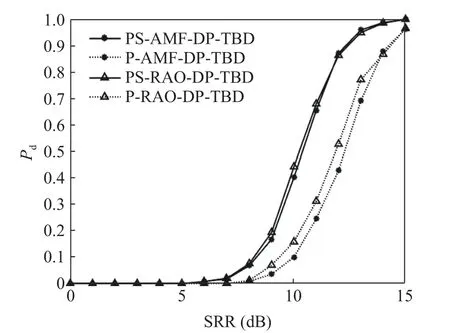
Fig.4 Accurate tracking probability when L=MN +1

Fig.5 Detection probability when L=MN/2

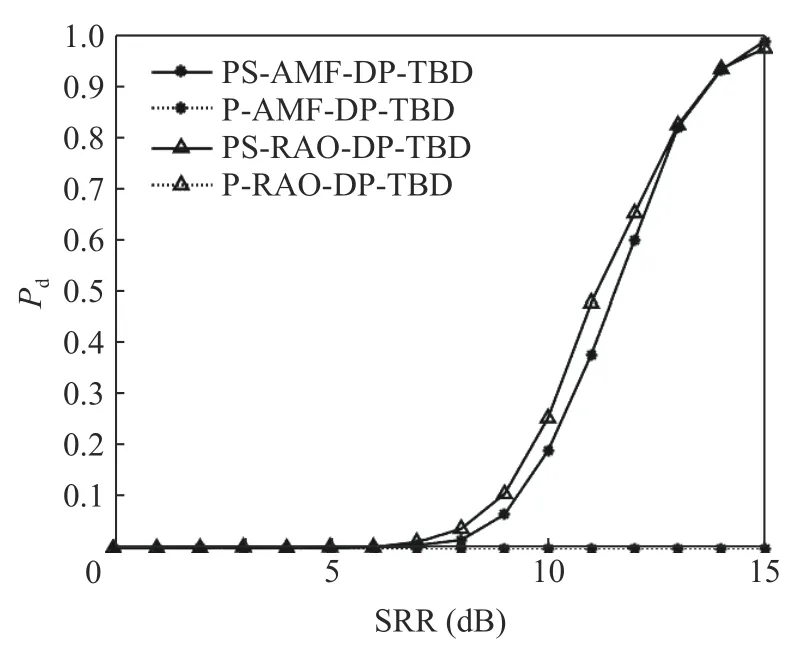
Fig.6 Accurate tracking probability when L=MN/2

As can be seen From Fig.1 and Fig.2, when the secondary data is sufficient, the four methods can work normally.Moreover, the PS-RAODP-TBD and the PS-AMF-DP-TBD algorithms have better detection performance and tracking accuracy.When the detection probability is 0.9,the detection probability of the PS-RAO-DPTBD is slightly higher than that of the PS-AMFDP-TBD.Compared with the P-RAO-DP-TBD,the PS-RAO-DP-TBD has a detection performance improvement of less than 1 dB.Compared with the P-AMF-DP-TBD, the detection performance of the PS-AMF-DP-TBD is improved by over 1 dB.When the accurate tracking probability is 0.9, the accurate tracking probability curves of the four almost coincide.The PS-RAO-DP-TBD and the PS-AMF-DPTBD have a performance improvement of about 1 dB compared with the P-RAO-DP-TBD and the P-AMF-DP-TBD.

Fig.3 and Fig.4 show that when the secondary data is slightly insufficient, the four methods can also work normally, and the PSRAO-DP-TBD and the PS-AMF-DP-TBD algorithms have better detection performance and tracking accuracy.When the detection probability is 0.9, the detection performance of the PSRAO-DP-TBD is nearly 1 dB better than that of the PS-AMF-DP-TBD.Compared with the PRAO-DP-TBD, the detection performance of the PS-RAO-DP-TBD is improved by about 2 dB.Compared with the P-AMF-DP-TBD, the detection performance of the PS-AMF-DP-TBD is improved by over 2 dB.When the accurate tracking probability is 0.9, the accurate tracking probability curves of the PS-RAO-DP-TBD and the PS-AMF-DP-TBD almost coincide, while the P-RAO-DP-TBD and P-AMF-DP-TBD have the same situation.Compared with the P-RAO-DPTBD and the P-AMF-DP-TBD, the PS-RAODP-TBD and the PS-AMF-DP-TBD have a performance improvement of about 2 dB.

According to Fig.5 and Fig.6, when the secondary data is severely insufficient, the PRAO-DP-TBD and the P-AMF-DP-TBD algorithms have become ineffective, while the PSRAO-DP-TBD and the PS-AMF-DP-TBD algorithms still have good detection and tracking performance.When the detection probability is 0.9,the PS-RAO-DP-TBD has more than 2 dB improvement over the PS-AMF-DP-TBD algorithm.The accurate tracking probability curves of the PS-RAO-DP-TBD and the PS-AMF-DPTBD cross.When the signal-to-reverberation ratio is below 13.5 dB, the accurate tracking probability of the PS-RAO-DP-TBD is higher than that of the PS-AMF-DP-TBD.

The greater the number of secondary data,the higher the estimation precision of reverberation covariance matrix.The number of secondary data based on persymmetry and symmetric spectrum is twice that of the persymmetry structure.Therefore, when the secondary data is sufficient and slightly insufficient, the detection accuracy and tracking accuracy of STAD-DPTBD algorithm based on persymmetry and symmetric spectrum are better than that of STADDP-TBD algorithm based on persymmetry.However, when the secondary data is seriously insufficient, the number of secondary data based on persymmetry and symmetric spectrum is slightly less than twice of the space-time dimension,while the number of secondary data based on persymmetry is less than space-time dimension.Therefore, when the secondary data is seriously insufficient, STAD-DP-TBD algorithm based on persymmetry becomes ineffective, while the STAD-DP-TBD algorithm based on persymmetry and symmetric spectrum can work normally.

In addition, the time cost of different algorithms is compared in Tab.2.

Tab.2 Comparation of time cost

As can be seen from Tab.2, the time cost of the proposed algorithm is basically the same as that of the algorithm based on persymmetry.

5 Conclusion

This article aims to address the issue of algorithm performance degradation caused by insufficient secondary data in the homogeneous reverberation background.The persymmetric symmetry and the spectral symmetry are combined and introduced into the binary hypothesis testing model.The hypothesis testing problem is transformed from the complex domain to the real domain, which is equivalent to increasing the length of the secondary data to four times, effectively improving the estimation accuracy of the reverberation covariance matrix.The PS-AMFDP-TBD algorithm and PS-RAO-DP-TBD algorithm are proposed based on the AMF test and the RAO test respectively.The simulation results show that when the secondary data is insufficient, the new method has higher robustness.The new method solves the problem of reduced target detection performance with small sample data, effectively improving the target detection and tracking performance of the sonar system.

The proposed algorithm is based on the ideal target sampling model of point-like target, which assumes that the target echo appears at the sampling time without energy leakage.In fact, the energy leakage often exists, so it is necessary to consider how to improve the robustness of STAD-DP-TBD algorithm in this case.