WSN Mobile Target Tracking Based on Improved Snake-Extended Kalman Filtering Algorithm
Duo Peng, Kun Xie, Mingshuo Liu
Abstract: A wireless sensor network mobile target tracking algorithm (ISO-EKF) based on improved snake optimization algorithm (ISO) is proposed to address the difficulty of estimating initial values when using extended Kalman filtering to solve the state of nonlinear mobile target tracking.First, the steps of extended Kalman filtering (EKF) are introduced.Second, the ISO is used to adjust the parameters of the EKF in real time to adapt to the current motion state of the mobile target.Finally, the effectiveness of the algorithm is demonstrated through filtering and tracking using the constant velocity circular motion model (CM).Under the specified conditions, the position and velocity mean square error curves are compared among the snake optimizer (SO)-EKF algorithm, EKF algorithm, and the proposed algorithm.The comparison shows that the proposed algorithm reduces the root mean square error of position by 52% and 41% compared to the SOEKF algorithm and EKF algorithm, respectively.
Keywords: wireless sensor network (WSN) target tracking; snake optimization algorithm; extended Kalman filter; maneuvering target
1 Overview
Tracking maneuvering targets in wireless sensor networks (WSN) is a research hotspot nowadays.For the maneuvering target, firstly, the trajectory data of the mobile target is collected in real time through the wireless sensor network, and then the position and motion state of the maneuvering target are predicted in real time according to the collected trajectory data.The system is designed in order to complete the maneuvering target motion state acquisition and tracking location.
There are currently two main methods for achieving WSN target tracking, one of which is obtaining the target trajectory through localization.Existing localization algorithms can be divided into two categories based on whether they involve ranging: ranging-based algorithms and non-ranging-based algorithms.Distancebased algorithms mainly include measurements of angles and distances, such as received signal strength indication (RSSI), time of arrival(TOA), time difference of arrival (TDOA), and angle of arrival (AOA).Non-ranging-based algorithms rely on node connectivity, such as hop count-based localization, and do not require any additional hardware support.Typical algorithms in this category include DV-Hop and approximate point-in-triangulation test (APIT) algorithms.These algorithms usually have higher tracking real-time performance but poorer tracking accuracy.
The second category of the methods is based on tracking prediction using sampled data.One method is filtering prediction, where common filtering algorithms include Kalman filter (KF),extended Kalman filter (EKF) which is an improvement of KF, unscented Kalman filter(UKF), and particle filter (PF) based on Monte Carlo method.Another method is based on neural network prediction, which uses the observed sensor data values as input and the neural network’s predicted values as output to predict the motion trajectory of moving targets, and to predict and track targets based on the target information observed by the nodes.These methods have good compatibility in terms of tracking trajectory, but it is difficult to simultaneously meet the requirements of tracking accuracy and realtime performance.
Among them, the prediction method based on KF, which is easy to implement and has a good tracking effect on linear systems, has been widely studied by scholars at home and abroad.The algorithm has the problem of obvious decline in tracking performance for nonlinear motion systems.In practical application, mobile targets usually move in a nonlinear motion mode, so many scholars improve the KF and propose an EKF algorithm.EKF is a linearization approach method.The EKF is computationally more efficient than the UKF or PF.The EKF uses a linearization approach, which allows it to propagate the state estimate and covariance matrix using matrix operations.In contrast, the UKF and PF involve sampling-based techniques or higher-dimensional transformations, which can be more computationally expensive.
The filtering parameters of the traditional extended Kalman filter are relatively fixed, which leads to the degradation of the performance of the algorithm.Among them, the filter parameterQrefers to the covariance of the covariance matrix of the noise in the maneuvering process,and the estimation accuracy of the main parameters and parameters of the shadow filter.The filtering parameterRrefers to the covariance of the covariance matrix of the measured noise, which mainly determines the correction speed of the filter.The improper value of filter parameters will lead to filter divergence, which will lead to a significant decrease in tracking accuracy.Therefore,many domestic and foreign scholars improve EKF.A modified EKF based on back propagation (BP) neural network is proposed in Ref.[1]to improve the accuracy of tracking.However,the large amount of calculation of BP neural network will reduce the efficiency of the system.An EKF tracking algorithm based on RSSI ranging model modification is proposed in Ref.[2].However, RSSI ranging instability will seriously affect the accuracy of tracking.In Ref.[3], a particle swarm optimization algorithm is proposed to modify the covariance matrix of the EKF to improve the tracking accuracy.However, when dealing with the problems in the dynamic environment, the particle swarm optimization algorithm may change rapidly, which will make the algorithm unable to adapt to the change.As a result, a good tracking effect can not be achieved in the nonlinear motion model with large noise.And the above algorithms are all improved target tracking algorithms under the assumption of known noise, but in practical application, the impact of noise on maneuvering targets is often unknown in advance [4].
Therefore, this paper proposes an EKF target tracking based on the improved improved snake optimization algorithm (ISO) optimization algorithm, which has a good tracking effect on the maneuvering target trajectory generated by the randomly generated noise value.Firstly,the algorithm uses the sensor network to obtain the data of the maneuvering target, and according to the obtained data, the ISO-EKF algorithm is used to dynamically search the optimal parameters to reduce the filtering error and improve the accuracy of tracking.Through the comparison of the standard EKF and snake optimizer (SO)-EKF algorithms, it is found that the filtering error of this algorithm is smaller than that of the two above algorithms.
2 EKF Algorithm
EKF algorithm is an improved algorithm based on Kaman filtering algorithm [5].Through Taylor series expansion of the state equation and measurement equation of nonlinear system, the higher order term will be ignored and only the first order term will be taken.At the same time,Jacobian matrix is used to replace the filter linear transformation in Kaman filtering algorithm,and the nonlinear problem is linearized.Then the Kaman filtering algorithm is used to estimate the parameters, and the trajectory prediction of nonlinear maneuvering targets is realized [6-8].The state equation and measurement equation of EKF system are as follows
wherefandhare the state function and observation function of the system, and the state vector of the system motion of the maneuvering target at timei,Xirepresents the system vector of the maneuvering target system at timei,Zirepresents the observation vector of the maneuvering target at timei,Ui-1represents input vectors for system control,Wi-1~N(0,Q),Vi~N(0,R).
whereAis the state transition matrix of the system,Iis the unit vector,Kiis the filter gain,Pi|i-1andPiare the covariance matrix of prediction error and the covariance matrix of estimation error, respectively,Hiis the observation matrix.The initial values are all unit matrices.e0is error covariance matrix.
The flow of EKF algorithm includes the following steps: first, according to the motion model and observation model of the system, the state transition equation and observation equation are established, and then, through the prediction steps (3) to step (6), the state estimation value and covariance matrix of the current moment are predicted by using the state transition equation and the state estimation value of the previous time.Then, through the update steps (7)-(9),using the observation equation and the observations at the current time, the predicted state estimates and covariance matrices are corrected, and the final state estimates and covariance matrices are obtained.However, from the above formula,in the traditional EKF, the filtering parametersQandRare fixed values, and if not selected properly, it will lead to filtering divergence,which will seriously affect the tracking accuracy.
3 Improvement Strategy
3.1 SO Algorithm
SO algorithm (SO) was proposed by Fatma A.Hashim and Abdelazim G.Hussien in 2022.Compared with the traditional meta-heuristic algorithm, snake optimization algorithm has better global search ability and can find the global optimal solution.In addition, the modified snake optimization algorithm also has good convergence and robustness.The main reason comes from the mating behavior of snakes.If the temperature is low and food is available, the mating behavior of snakes occurs.Otherwise, snakes will only search for food or eat existing food.Based on this, the search process of the snake optimization algorithm is divided into two stages: exploration and development.Exploration describes environmental factors, such as cold places and food, during which there is no situation where snakes search for food in their surrounding environment.
The survey phase described that due to environmental and food factors, snakes do not search for food around them.IfG<0.25, snakes will search for food through random positions and update their positions.The simulation during the exploration phase is as follows
whereGis threshold, rand denotes the random number in [0, 1],c is 0.05,Xmaxis the upper boundary of the algorithm,Xminis the lower boundary of the algorithm.The expressions ofAfandAmare as follows
wherefrand,fandfrand,mare the fitness values of male and female, respectively.fi,fandfi,mare the fitness values of male and female individuals in the first position.
During the development phase,Gis greater than 0.25; at greater than 0.6, the temperature and food meet the conditions, looking for food,and its location updating formula is as follows
whereXfoodis the location of the food, c3is 2,which is the best position for individual snakes.
During the development phase, if the food is available and the area is cold, the mating process occurs.There are some situations in the mating process, that is, combat mode or mating mode.In combat mode, each male will fight to get the best female, and each female will try to choose the best male.In the mating mode, the mating behavior of each pair of snakes depends on the amount of food available.In the search space, if mating occurs, the female may lay eggs and hatch into new snakes.The simulation of the development phase is as follows.
When the individual snake enters combat mode, the position update formula is as follows
whereXi,m(t) is the position of thei-th female snake,Xbest,fis the best position in the female snake group, FM is the combat capability of female snakes.
whereXi,f(t) is the position of thei-th male; FF is the female combat ability;Xbest,mis the best position in the female snake group; rand is a random number within the range of [0, 1]; FM is the combat ability of male snakes.
In mating mode, the mating ability of male and female snakes is calculated as follows
wherefi,fis the fitness value of thei-th male individual,fi,mis the fitness value of thei-th male individual.
If the snake eggs hatch, choose the position replacement of the snake with the worst adaptation value, which can be expressed as
whereXworst,mis the worst individual in the male snake group; andXworst,fis the worst individual in the female snake group.
3.2 ISO Algorithm
3.2.1 Nonlinear Convergence Factor
The SO algorithm has a good optimization ability, but the convergence factor of the SO optimization algorithm decreases linearly with the increase of the number of iterations, which leads to the local optimization.The goal that is more suitable for the algorithm should be in the early stage of the algorithm.With the increase of iteration, the convergence factor decreases slowly, so that the snake group can search the target in a larger range to achieve the purpose of maximizing the global search.In the middle and later stages of iteration, in order to quickly reduce convergence and concentrate snake targets, fast convergence can promote the effectiveness of optimization.Therefore, a convergence factor is improved in this paper, the attenuation degree is low at the beginning, and the snake can move with a larger stride.In the later stage, the attenuation degree of ambient temperature Temp and food quantityDincreases, and the snake movement stride decreases, so the optimal solution can be found more accurately.Thus, it can more effectively balance the development ability of global search and the mining ability of local search, so that the improved SO algorithm can better adapt to the more complex search process.The expression is as follows
whereTrepresents the total number of iterations, andtrepresents the current number of iterations.
3.2.2 Cubic Chaotic Cubic Map
The population initialization of most swarm intelligence optimization algorithms is usually randomly generated.This method often leads to uneven distribution of the initial population,which affects the performance and accuracy of the optimization process.The distribution of initial solutions in the solution space has a significant impact on the algorithm’s ability to solve complex optimization problems.If the initial population can randomly and non-repetitively traverse all states in the solution space, and fully utilize the information in the search area, it can effectively enhance the algorithm’s global search capability and avoid falling into local optimal solutions due to reduced population diversity in the later iterations of the algorithm.Chaos phenomena possess characteristics such as randomness, regularity, and thoroughness, and therefore chaos operators are often used for population initialization.This paper proposes a cubic chaos mapping to generate a more evenly distributed initial population.It uses chaotic mapping to generate a sequence of random numbers instead of the pseudo-random number sequences used in traditional optimization algorithms.In order to enhance the population diversity of the standard SO algorithm and improve the optimization efficiency, the ISO algorithm adopts the strategy of using cubic chaos mapping for population initialization.By utilizing the randomness and thoroughness of chaotic variables, a more diverse chaotic initial population is generated.The cubic chaos mapping is chosen for its higher iteration speed, better thoroughness, and more even distribution for initializing the population.By mapping the chaotic sequence generated by the chaotic mapping into the solution space, a more diverse initial population is obtained, thereby expanding the search range of the algorithm and improving the accuracy and performance of the optimization algorithm.Its expression is as follows
whereρ= 2.595,N0=0.3,Nnis the current position of the population.
This article introduces the Sine mapping to increase the randomness of the initial population and make its distribution more uniform.It also divides the attack range based on individual fitness to increase attack efficiency.Individual position updates are achieved through linear transformation.While improving the convergence performance of the basic snake optimization algorithm,the design of the coefficient matrix is utilized to eliminate the influence among different dimensions during the iteration process.
Comparing the improved snake algorithm’s optimization performance proposed in this article, we selected the Sphere function for comparison.The population size was set to 30, and the number of iterations was set to 200.We compared the dragonfly optimization algorithm (DBO),grey wolf optimization algorithm (GWO), whale optimization algorithm (WOA), northern goshawk optimization algorithm (NGO), and the proposed algorithm.We independently ran 30 simulations of the test function and compiled the experimental results.The mapping effect of cubic chaotic cubic map is shown in Fig.1 and Fig.2.

Fig.1 Cubic chaos cubic map distribution map
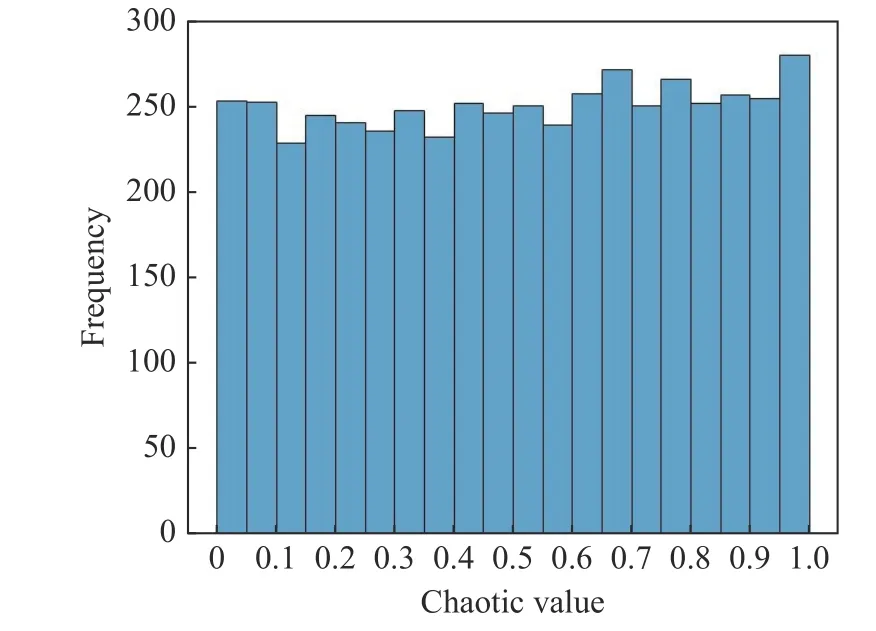
Fig.2 Cubic chaos cubic mapping frequency statistics
According to Fig.3, the algorithm proposed in this article has the highest convergence speed,indicating that the optimization ability of the F1 function proposed in this article is very stable,and the repeatability accuracy is higher compared to other algorithms.It can be seen from Fig.4 and Fig.5 that for functions F2 and F3,the results are similar to F1, and the optimization performance of the algorithm proposed in this article is still the best.Additionally, the fitness value obtained by the algorithm proposed in this article is the smallest, and the average fitness value obtained by the optimization algorithm proposed in this article is closer to the theoretical optimum value of 0, indicating better optimization performance.

Fig.3 Comparison of the sphere function of F1
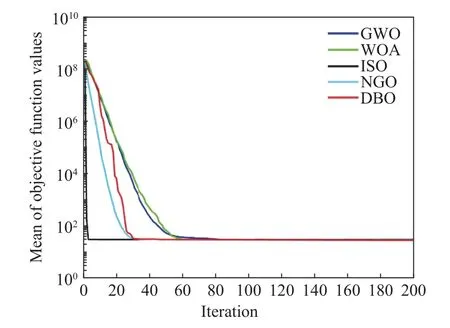
Fig.4 Comparison of the sphere function of F2
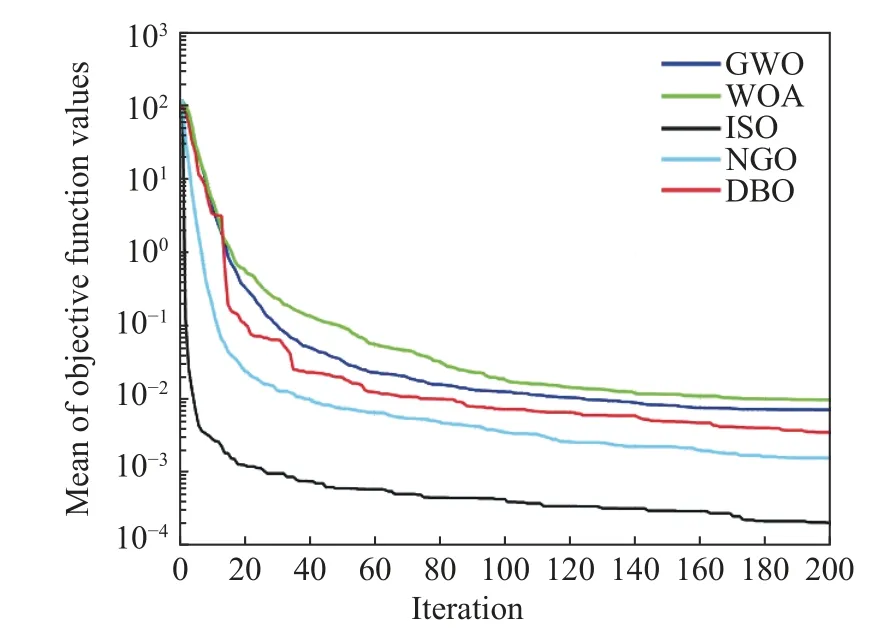
Fig.5 Comparison of the sphere function of F3
4 ISO-EKF Algorithm
In this paper, the ISO algorithm is used to dynamically optimize theQandRvalues in EKF, so that the filter can dynamically adjust the parameters according to the change of the motion state of the maneuvering target.The algorithm initializes the variable first, then estimates the parameters of the maneuvering target according to the Eqs.(3)-(9), takes the noise covariance matrix parameterσas the individual position of the optimization algorithm, optimizes the random noise with covarianceQandRvalues, adds it to the observations and estimates of the ISO algorithm, and takes the current time observations and estimated values as the fitness function of the ISO algorithm.New filtering parameters can be obtained for each repetition,and the accuracy of the filtering parameters generated by this iteration can be judged according to the fitness value calculated by the fitness function.The smaller the fitness value is, the smaller the difference between the predicted value and the observed value is.The selection of filtering parameters is more accurate [9-14].The expression of the fitness function is as follows
whereσiis the position of individualI, ZPjiis the observed valueσiof theσidimension with the parameterI,Iis the estimated value of theσi-th dimension with the parameter, EPjiis the actual value, KP is error amplification factor,mis the current sampling time.
Considering that the ISO algorithm may take too long to calculate each filter, set a number of iterationshquery EKF to execute the ISO algorithm for parameter optimization after everyhconsecutive execution.According to the operation process of EKF, use ISO to dynamically optimize it, such as the following steps.
1) Step 1
Initialization.The snake population is initialized, and the cubic chaotic cubic map is used to make the snake population evenly distributed in the search space, and the maximum number of iterations, food and temperature trigger threshold are set.
2) Step 2
Determine the objective function.According to the EKF algorithm process, the fitness function is determined as shown in Eq.(24).
3) Step 3
Divide the population into male and female groups, set the fitness function, and calculate the corresponding fitness to find the best male and female individuals.
4) Step 4
Define the ambient temperature Temp and food quantityDaccording to Eqs.(21) (22).
5) Step 5
Determine whether the individual is only looking for food or fighting and mating according to the size of the food quantityD.If the snake is 0.25, then only look for food and update the individual position of the snake according to Eqs.(10) (11).
6) Step 6
If the food is sufficient and Temp>0.6, and the snakes only look for food and eat existing food, update the location according to Eq.(14).
7) Step 7
Enter the combat mode and the mating mode according to the random number of the mode, update the position of the combat mode according to Eqs.(15) (16), replace theAmin the combat mode with Eqs.(17) (18) respectively, replace the best individual with the current individual, and update the position.If the eggs hatch, pick the worst individuals and replace them.
8) Step 8
Process the updated position, update the best value of individual history, judge whether it reaches the number of iterations, enter the next iteration if it is not satisfied, and output the best position at the end of the iteration if it is satisfied.The flow chart of the ISO-EKF algorithm is shown in Fig.6.
In this paper, the ISO-EKF algorithm is used to dynamically search the optimal parametersQandRto reduce the filtering error and greatly improve the problem that it is difficult to estimate the initial value when tracking non-linear maneuvering targets.
5 Simulation Experiment and Analysis
5.1 WSN Modeling
In this paper, the performance test is mainly aimed at the uniform turning movement model.The motion state equation of the uniform turning motion model is as follows
whereΩis the angular velocity during turning motion,Gkis for the motion state matrix,xk+1is the measurement equation,Wkis a Gaussian noise sequence, Δtkis the time interval between two consecutive measurement times.

Fig.6 ISO-EKF process flowchart
Aiming at the tracking problem in the WSN area, it is assumed that the sensors in the sensor network are all of the same type.The performance of target tracking algorithms is usually reflected by the size of the tracking accuracy,which is typically represented by the mean square root error as [15-20]
whereγiis a Gaussian random noise,niis the observation noise of the sensor, (x,y) is the position of the target at timet,(xi,yi) is the position of sensori,uiis the random noise generated by covarianceQ.
In the simulation experiment, RMSE is used as the standard to measure the tracking effect,and the formula is as follows
where RMSE is the normalized average positioning error of the node,nis the number of samples taken, (x0(i),y0(i)) is the true position of the target at timei, (x¯(i),y¯(i)) is the target position for each algorithm at timei.
5.2 Simulation Conditions
Fifty sensors are randomly arranged in the monitoring area of 100 m × 100 m wireless sensor network.The communication radius of the sensor is set to 30 m, the sampling period is set to 0.1 s,and the number of sampling points is set to 50.ParameterQis set to a random value in 0.000 1,and parameterRis set to a random value in[21, 22].In the ISO algorithm, the populationMis set to 20, and the maximum number of iterations is set to 100.The food quantity thresholdGwas set to 0.25 and the temperature threshold Temp was set to 0.6.
The initial value of theXdirection of the track is 35 m, the initial value of theYdirection is set to 10 m, the initial velocity values of theXdirection andYdirection are set to 5 m/s, and the velocityΩis set to 0.185.In the comparison algorithm, the particle count of the PF algorithm is set to 30.
After establishing the target model and setting the initial conditions for simulation, the ISO algorithm is used to track and filter the trajectory, and the trajectory comparison graph is shown in Fig.1.In order to verify the effectiveness of the algorithm, this paper uses the ISOEKF algorithm, SO-EKF algorithm, EKF algorithm, PF algorithm, and UKF algorithm to track the moving target 100 times, and uses the root mean square error (RMSE) as the standard to evaluate the performance of the algorithms.Tab.1 shows the comparison of tracking errors for the three algorithms.The simulation results show that in terms of tracking accuracy and error, the order of superiority of the algorithms is ISO-EKF, SO-EKF, PF, UKF.

Tab.1 Comparison of tracking errors
Fig.7 and Fig.8 depict the RMSE variation curves in theXandYdirections.It is evident that the ISO-EKF algorithm outperforms the SO-EKF and EKF algorithms in terms of RMSE in both directions.Additionally, the ISOEKF algorithm exhibits smaller fluctuations,indicating its robustness and accuracy in tracking.This can be attributed to the fact that the ISO-EKF algorithm is not influenced by previous position prediction results.On the other hand, the UKF and PF algorithms lack a dynamic observation of noise values, resulting in fixed filtering parameters and subpar tracking performance.
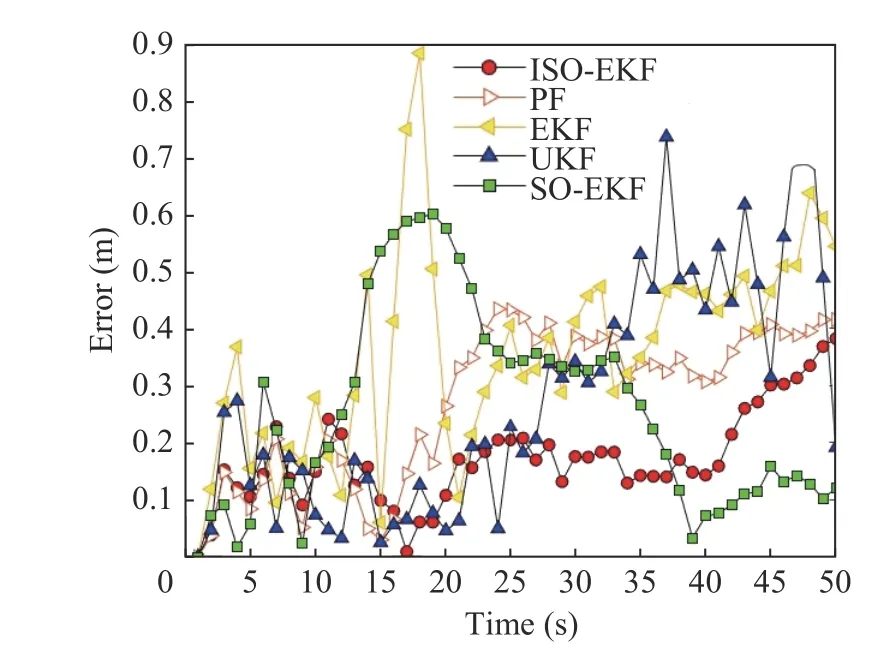
Fig.8 Time-dependent curve of Y-direction position RMSE of RMS
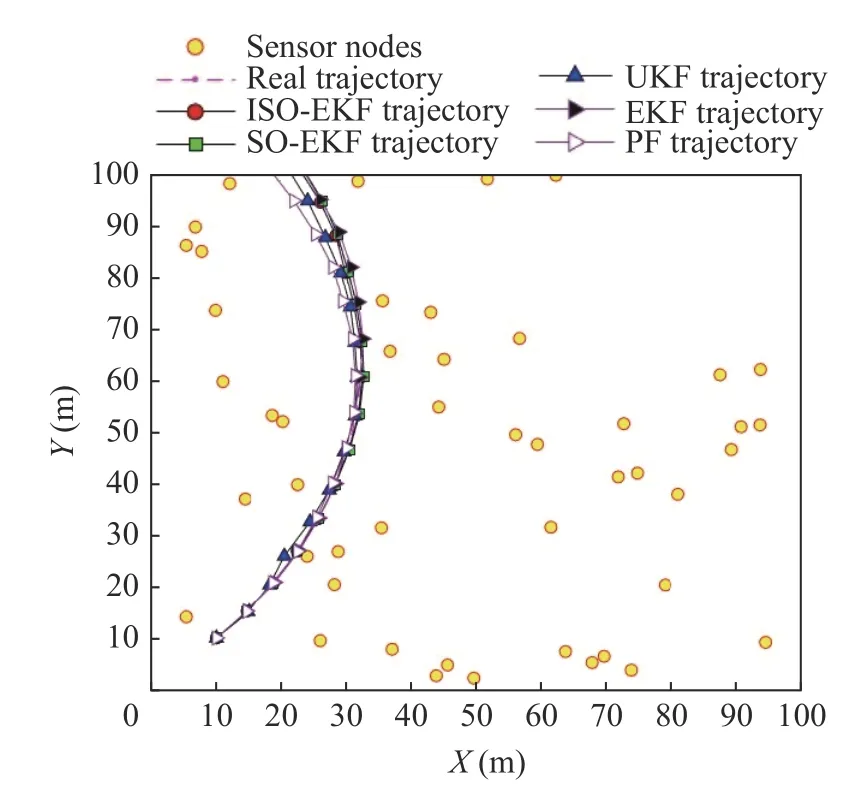
Fig.9 Trajectory comparison
The tracking trajectories of the target in the two dimensional (2D) space are compared as shown in Fig.9.From Fig.9 and Tab.1, it can be seen that the tracking trajectory of ISO-EKF is almost identical to the true trajectory, with a RMSE of only 0.334 81.It can be seen that the ISO algorithm is effective for tracking the target in a nonlinear model.Fig.10 shows the comparison of position errors among the three algorithms.From Tab.1, Fig.7, and Fig.8, it can be seen that the RMSEs of position and velocity are reduced compared to the EKF algorithm and SOEKF algorithm.It can be concluded that the ISO-EKF algorithm has good tracking performance in nonlinear motion systems.
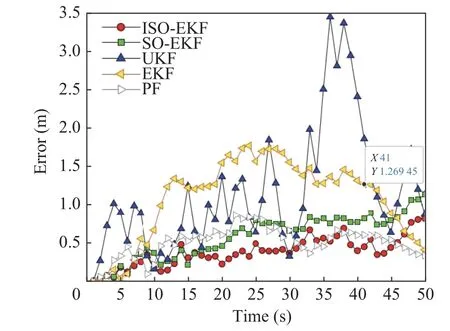
Fig.10 Root mean square (RMS) error comparison
The velocity RMSE variation curves in theXandYdirections are depicted in Fig.11 and Fig.12, respectively.It is evident that the ISOEKF algorithm exhibits lower RMSE in both theXandYdirections compared to the comparison algorithms.Additionally, the ISO-EKF algorithm demonstrates reduced fluctuation.These findings provide evidence that the ISO-EKF algorithm is less susceptible to the influence of previous position prediction results, thereby ensuring superior tracking stability and accuracy.
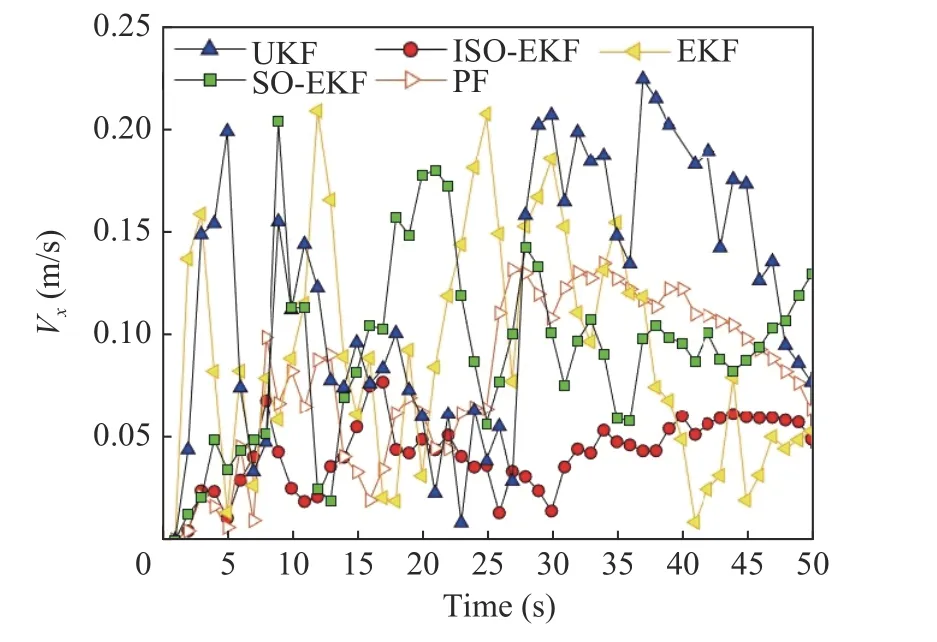
Fig.11 Time-dependent curve of X-direction velocity RMSE of RMS

Fig.12 Time-dependent curve of Y-direction velocity RMSE of RMS
As the maneuvering target approaches the endpoint, the guidance acceleration of the maneuvering target tends to zero, leading to a decrease in the observability of the system.Additionally, the measurement noise increases, and the unimproved algorithm exhibits a sudden increase in speed estimation for the maneuvering target.If this large error estimate is fed back to the system, it significantly affects the estimation accuracy.In comparison to other comparative algorithms, the algorithm proposed in this article effectively mitigates the increase in filtering speed error, resulting in more accurate positioning of maneuvering targets.
5.3 Algorithm Complexity Analysis
Due to the limited connectivity resources in wireless sensor networks, when designing algorithms,not only the tracking accuracy but also the complexity of the tracking algorithm should be considered as an important factor for the effectiveness of the tracking algorithm.Compared to the traditional intelligent optimization improved extended Kalman filter algorithm, this algorithm in this paper approximates the roots of nonlinear equations by using adaptive weighting factors.One of the advantages of this approach is its fast convergence speed, which greatly reduces the complexity of the optimization algorithm, especially near the roots.By improving the convergence factor, the snake algorithm achieves a better balance between global search and local search, enabling it to adapt more effectively to complex search processes and significantly reducing the complexity of the algorithm.This allows for better tracking performance in applicable scenarios [23-29].
This article conducted 100 simulation experiments using three types of filtering EKF algorithm, SO-EKF algorithm, and the algorithm proposed in this article.The comparison table of the timeliness of the three algorithms is shown in Fig.13.Due to the addition of adjustment factors to the snake optimization algorithm, the algorithm proposed in this article has the best timeliness.
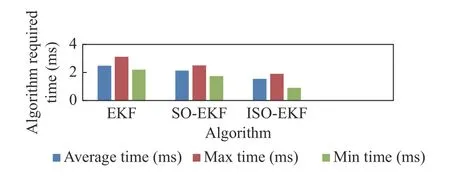
Fig.13 Algorithm timeliness comparison chart
6 Summary
In this paper, an EKF target tracking algorithm based on improved snake optimization algorithm is proposed.First of all, the data of the maneuvering target is collected in real time by the wireless sensor network, and the parameters are input into the EKF algorithm, and then the ISO algorithm is used to optimize the filter parametersQandR, thus forming the ISO-EKF algorithm.The algorithm can adaptively adjust the parameters according to the change of the motion state,so as to obtain higher tracking accuracy.The comparison shows that the RMSE of the proposed algorithm is 52% and 41% lower than that of SO-EKF algorithm and EKF algorithm,respectively.In addition, how to save energy while ensuring the accuracy of tracking in order to prolong the network life cycle is the next step of the ISO-EKF algorithm.
In addition, how to save energy on nodes while ensuring tracking accuracy to extend the network lifetime is the next step that the algorithm proposed in this article needs to solve[29, 30].
 Journal of Beijing Institute of Technology2024年1期
Journal of Beijing Institute of Technology2024年1期
- Journal of Beijing Institute of Technology的其它文章
- Improved Weighted Local Contrast Method for Infrared Small Target Detection
- Equalization Reconstruction Algorithm Based on Reference Signal Frequency Domain Block Joint for DTMB-Based Passive Radar
- A Novel Clutter Suppression Algorithm for Low-Slow-Small Targets Detecting Based on Sparse Adaptive Filtering
- An Efficient Radar Detection Method of Maneuvering Small Targets
- Detection of UAV Target Based on Continuous Radon Transform and Matched Filtering Process for Passive Bistatic Radar
- Robust Space-Time Adaptive Track-Before-Detect Algorithm Based on Persymmetry and Symmetric Spectrum
