An Efficient Radar Detection Method of Maneuvering Small Targets

Hongchi Zhang, Yuan Feng, Shengheng Liu

Abstract: Detection of maneuvering small targets has always been an important yet challenging task for radar signal processing.One primary reason is that target variable motions within coherent processing interval generate energy migrations across multiple resolution bins, which severely deteriorate the parameter estimation performance.A coarse-to-fine strategy for the detection of maneuvering small targets is proposed.Integration of small points segmented coherently is performed first, and then an optimal inter-segment integration is utilized to derive the coarse estimation of the chirp rate.Sparse fractional Fourier transform (FrFT) is then employed to refine the coarse estimation at a significantly reduced computational complexity.Simulation results verify the proposed scheme that achieves an efficient and reliable maneuvering target detection with -16dB input signal-to-noise ratio (SNR), while requires no exact a priori knowledge on the motion parameters.

Keywords: small target; chirp; sparse fractional Fourier transform (FrFT)

1 Introduction

Radar detection of maneuvering small targets inevitably faces a technical dilemma.On the one hand, in order to improve the signal-to-noise ratio (SNR) and facilitate reliable detection and parameter estimation of weak components, observation time should be prolonged.On the other hand, the effect of range and Doppler walks induced by the maneuvering motion is exacerbated with an extended observation interval [1].Nevertheless, the vital importance of this problem still encourages many radar researchers to seek the solutions.Some relevant works are reviewed as follows.Substantial consecutive radar echoes can be integrated incoherently or coherently to improve the SNR.Typical methods in the former category include Radon transform [2], Hough transform [3], track-before-detection algorithm [4], etc.Because only echo amplitude is utilized while the phase information is totally ignored, these methods generally suffer from integration gain loss.Alternatively, long time coherent integration has been shown to be more effective.Various algorithms as for coherent detection are proposed.Some important advances in the past three years include timereversing transform [5], location rotation transform [6], discrete polynomial-phase transform(DPT) [7], and Radon Fourier transform [8, 9]based schemes.A coarse-to-fine strategy is proposed based on segmented DPT and extends the maximum unambiguous range for chirp rate estimation using coprime slow-time sampling beforehand [1].

Fractional Fourier transform (FrFT) represents an intuitive and natural domain for the time-frequency analysis of chirp signals, since chirp basis functions are employed to project the original time sequence onto a rotated time axis.We also know that, the scattered electromagnetic energy by multiple maneuvering targets usually manifests itself as chirps in the radar return signal.Thus, by carefully choosing appropriate FrFT rotation angle, each of these target chirps can be transformed to impulses and exhibits sparsity in the matched fractional Fourier domain (FrFD).In the light of this observation, sparse FrFT (SFrFT) is proposed based on the sampling-type numerical algorithm and efficient detection of uniformly accelerating targets is realized [10].On this basis, maneuvering target detection in the presence of strong clutters is considered in and a robust SFrFT is proposed [11].Highly maneuvering targets are further considered and the high-order phase modulation is handled by sparse fractional ambiguity function [12].However, to implement the above algorithms, the prior knowledge on the exact sparsity of targets is essential and brute force searching, which is computationally expensive, is required to obtain the optimal rotation angle.Chirp-rate estimation of multi-component linear frequency modulated (LFM) signal is realised by FrFT and the estimated interval of chirp-rate deducing [13].A short-time FrFT method with adaptive window function is proposed to overcome the shortcomings of single and fixed window function in traditional short-time FrFT, and a time-frequency distribution that better matches the desired signal is achieved [14].An efficient segmented DPT is designed in [15] to yield a coarse parameter estimation of weak chirp signals.But the unambiguous range of difference frequency via segmented DPT, which is associated with the chirp rate estimation, is very limited.This in turn impedes its application to the detection of highly maneuvering targets.In [1],the difference frequency scope is extended and the segmented DPT is modified using coprime sampling, and then the parameter estimation is further refined using an optimized SFrFT, where the requirement of false-alarm rate in practical radar detection of weak target is considered.Because the inter-segment integration with slowtime sampling rate is calculated in vertical direction, energy diffusion of Doppler walks induced by the maneuvering motion is not eliminated.The detection performance will be limited when the input SNR is very low.

In this work, the inter-segment integration is calculated in the optimal direction to obtain the coarse estimation of the chirp rate to enhance the SNR.The parameter estimation is further refined using an optimized SFrFT, where the requirement of false-alarm rate in practical radar detection of small target is considered.The two above stages collectively constitute an improved coarseto-fine strategy for efficient radar detection of maneuvering small targets.The rest of this paper is organized as follow.Section 2 presents the signal model and the proposed coarse estimation algorithm flow.Section 3 descripts the further refined parameter estimation by using an optimized SFrFT.Simulation results and analyses are given in Section 4.Conclusions are drawn in Section 5.

2 Coarse Estimation

The signature of the maneuvering targets is captured by the chirp components in the echo signal.Hence, the problem under investigation, namely,radar detection of maneuvering small targets, can be mathematically modelled as parameter estimation of low-SNR chirp components in the FrFD.We consider a generic noise-corrupted input signal ofN-point, which includesK-chirp components [1], as

wheren=0,1,···,(N-1) is the time-domain index, andtsrepresents the sampling interval.The termw[n] denotes the additive complex white noise, which is assumed to be Gaussian,i.e.,w～CN(0,σ2).The variablesAk,fk, andµkrespectively denote the amplitude, the initial frequency, and the chirp rate of thek-th chirp component, which are the primary parameters of interest in radar measurement.Similar to coprime segmentation in [1], segmentation is performed before coherent integration to allow parameter estimation of high chirp rate.Concretely, a positive integerLis selected as the segment length.As such, the total number of nonoverlapping segment length isP=round(N/L).Thereby givenn=l+pL, for anyp=0,1,···,(P-1) andl=0,1,···,(L-1) , the [p,l]-th entry in the reshaped discrete signal matrix can be derived from (1) as

where an arbitrary entry in the original input sequence (1) is mapped to a definite entry in the reshaped matrixs˜[p,l] by following the index relationship [p=n/L] andl=n-(p-1)L, andw˜(p,l) is the noise matrix.The neighboring entrys within the same column of the reshaped matrix are spacedLsamples apart.The first row in the reshaped matrixs˜[p,l] is

Thep-th row in the reshaped matrixs˜[p,l]can be rewritten as follows

The third exponential function term in (4)is consistent.Comparing (3) and (4), we can find that the initial frequency shifts fromfkto(fk+µkpLts).Suppose that we perform fast Fourier transform (FFT) with respect tolin each row.Letm=0,1,···,(L-1) denote the frequency-domain index.The [p,l]-th entry is converted to

The initial frequency shift is showed as Fig.1.We readily infer from Fig.1 that, the energy of inter-segment coherent integration in every column is diffusion by Doppler migration.So it is valid only for zero or very small chirp rate.A natural thought is that the inter-segment coherent integration is performed in the bright line direction on Fig.1.In order to reduce the amount of calculation, the inter-segment coherent integration is performed by summing the modulus of every entry in column forS˜[p,m]

Inter-segment integration ofS˜[p,m] in bright line direction is

wheredis the shift factor in every row, which is determined by chirp rateµk, andm=0,1,···,L-1.The results of inter-segment integration in column and bright line direction on Fig.1 are shown as Fig.2.From Fig.2, it can be found that curve of inter-segment integration in column has a small platform, which will be submerged by noise when the input SNR is small.For comparison, a high sharp peak appears in the curve of inter-segment integration in the bright line direction.It is very conducive to detection of maneuvering small targets.However, the prior knowledge on the exact chirp rate is essential or the chirp rate is estimated by brute force searching, which is computationally expensive [1].In this work, an optimization method for chirp rate estimation is proposed to substitute brute force searching.

Fig.1 Diagram of Doppler migration, S NR =-2dB, L =105

Fig.2 Inter-segment integration

In order to better illustrate the principle of the proposed algorithm, only mono-chirp case is taken into account below.As such, we omit the subscriptkin the parameters.Note that, the conclusions and methodology can be easily generalized to more complicated multiple chirp component cases.From (7), we obtain the coarse estimation of chirp rate as

whereS[·] represents the result of inter-segment integration.The optimization problem (8) is solved by using one-dimensional searching technology, which is implemented by quadratic interpolation technology.The chirp rate coarse estimation is summarized in Algorithm 1.

Algorithm 1 Chirp rate coarse estimation 1: Inputs:˜S[p,m],{a,b},ε L, P, ;ˆµ a,b,L,P,ε, ˜S[p,m]=Opt-S( );

a,b,L,P,ε, ˜S[p,m]2: procedure Opt-S ( )3: Notice! The Cost_F must be a low single peak in[a, b]c=(a+b)/2 4: ;fa =Cost_F(a,L,P,ε, ˜S[p,m])5: ;fb =Cost_F(b,L,P,ε, ˜S[p,m])6: ;fc =Cost_F(c,L,P,ε, ˜S[p,m])7: ;b-a ≥ε 8: while do x a,c,b 9: calculate , by minimizing the quadratic interpolation function( );fx =Cost_F(x,L,P,ε, ˜S[p,m])10: ;a,b,c a,b,c,x 11: optain new from according to the relationship of the function values;12: end while ˆµ= c 13: return ;14: end procedure CostF x,L,P, ˜S[p,m]15: procedure ( )˜Sip[m,x]=∑P L2t2 s‖‖‖˜S[p,m†]‖‖‖2 16: ;m† =m-round(xp)17: ;˜Smaxip[x]=arg max p=1 Svp[m,x]18: ;m fvalue =-Smaxip[x]19: ;fvalue 20: return ;21: end procedure

3 Refining the Coarse Estimation by Sparse FrFT

Eq.(5) performs FFT for every row, and segmented signal lengthLis generally small.The estimated chirp rate can be considerably inaccurate due to the high noise level and the coarse resolution grid.In the light of these limitations,we further refine the parameter estimation in a significantly narrowed range in the fractional Fourier domain.Since the coarse estimated chirp rate has been obtained, the parameter estimation refining can perform by brute force searching in a small range.The phase correction SFrFT[16] is utilized to reduce the amount of FrFT computation.The specific algorithm can refer the Algorithm 2 in [1], and also, the optimization method similar to the Algorithm 1 in this paper can be used to further reduce the amount of operation.

4 Numerical Simulations

In this section, numerical simulations are provided to showcase the advanced performance of the proposed detection scheme for maneuvering small targets.In both simulations, we assume that the radar operates at a center frequency offc=3 GHz, and the pulse repetition interval is 0.125 mswhich corresponds to a sampling rate offs=8 000 Hz.The input SNR is -16 dB.We consider a single target with an initial velocity ofv=50 m/s and an acceleration rate ofa=10 m/s2.The corresponding initial frequency and chirp rate arefini=1 000 Hz andµ=200 Hz/s, respectively.In the coarse estimation of the chirp rate procession, the segment length isL=105, and the signal length isN=20 160.The total number of non-overlapping segment length isP=N/L=192.The initial estimation of chirp rate range is 100 Hz/s ≤µ≤300 Hz/s, which corresponds to the acceleration rate of the target in the range of 5 m/s2≤a≤15 m/s2.The results of the segmented FFT with segment lengthsL=105 are given in Fig.3.It can be found that the bright line caused by Doppler migration is Blur caused by noise.The coarse estimation of the chirp rate is obtained by Algorithm 1,µˆ=199.741 7 Hz/s.The inter-segment integrations along an oblique line direction are calculated 7 times.The oblique line search direction is determined by tentative chirp rate.The results of inter-segment integration in column and the estimated bright line direction in Fig.3 are shown as Fig.4.From Fig.4,we can readily see, a noticeable spike appears on the curve of optimal inter-segment integration direction, and multiple small amplitude peaks appear on the curve of inter-segment integration in column.The results corroborate that the proposed optimal coarse estimation of the chirp rate is very effective.To examine the effect of signal length on coarse estimation, simulations are performed on distinct signal lengths.The results of coarse estimation with 2 times and 8 times original signal length are given in Fig.5 and Fig.6.Comparing Fig.4, Fig.5 and Fig.6, it can be found that the SNR of optimal coarse estimation results is promoted with the increase of signal length, but no peaks can be observed on the curve with 8 times original signal length integrated in column.

Fig.3 Diagram of Doppler migration, signal lengthN

Fig.4 Inter-segment integration, signal lengthN

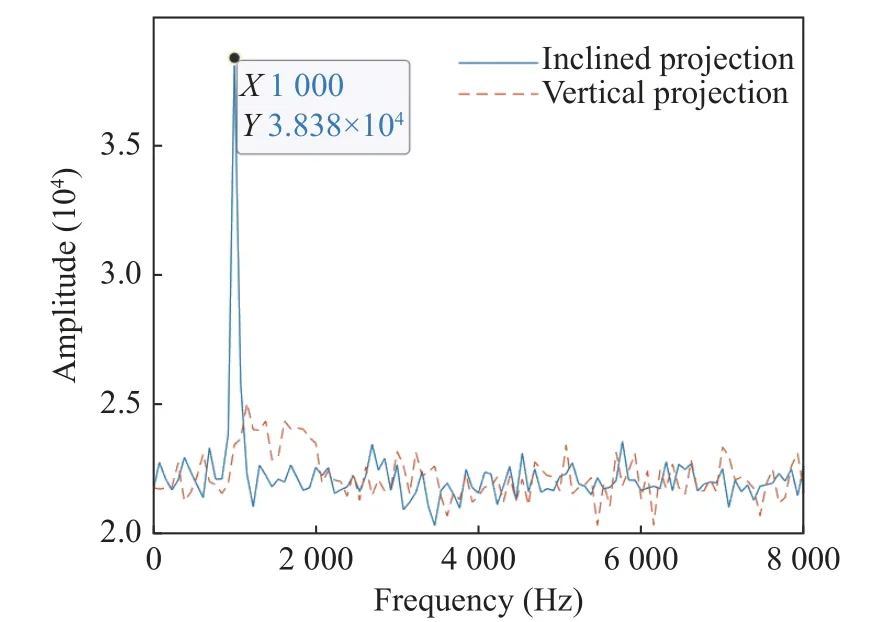
Fig.5 Inter-segment integration, signal length2N

Fig.6 Inter-segment integration, signal length8N

The results of discrete FrFT (DFrFT) and SFrFT using the rotation angle matched with coarse estimated chirp rate 199.741 7 Hz/s are provided in Fig.7.Local magnified view near the peak is given in Fig.8.Fine search is conducted and we find the maximum amplitude at the chirp rate 200 Hz/s, as shown in Fig.9.Fig.10 is its local magnified view near the peak.The signal length is selectedNs=32 768, and the other parameters are the same as coarse estimation.The center frequency is(fini+µNsts/2)=1 409.6 Hz/s.We also readily see from Fig.8 and Fig.10 that, the results of SFrFT can achieve a good approximation of DFrFT, and SFrFT refining lets the peak amplitude increase by 44.78.Meanwhile, the computational complexity is significantly reduced.

Fig.7 FrFT spectra using conventional DFrFT and SFrFT using rotation angles corresponding to the coarse chirp rate estimations

Fig.8 FrFT spectra and local zoomed results of Fig.7

Fig.9 FrFT spectra using conventional DFrFT and SFrFT using rotation angles corresponding to the refined chirp rate estimations

Fig.10 FrFT spectra and local zoomed results of Fig.9

5 Conclusion

A coarse-to-fine strategy is designed to help radar operators to observe highly maneuvering small targets that are otherwise difficult to detect.The target-scattered energy in the radar return is coherently integrated in the FrFD using an efficient sparsity-aware numerical algorithm termed optimized SFrFT.The optimized SFrFT allows custom configuration of false-alarm rate.But prior knowledge on exact sparsity and matched rotation angle is also required.Hence,we perform segmented coherent integration first,and then an optimal inter-segment integration is utilized to derive the coarse estimation of the chirp parameter.The potential of the proposed two-stage scheme is showcased in the numerical simulations.Non-coherent integration is used to obtain coarse chirp-rate estimation.The coherent integration can be utilized to further increase the accuracy.However, coherent integration results in higher complexity, and the proposed non-coherent integration method can estimate the chirp rate when the SNR is -16 dB.So noncoherent integration method is selected.In the presence of multiple chirp components, the optimization process of coarse estimation will have multiple maxima at multiple angles and the optimization algorithm will be more complicated.