微波感知测振技术及其在水轮机压力钢管水锤作用下振动形变分析中的应用

黄 波，毛柳明，张亦可，任继顺，张民威，何继全，李光明

(1.国网湖南省电力有限公司电力科学研究院，湖南 长沙 410007；2.北京中元瑞讯科技有限公司，北京 100085；3.邵阳学院机械与能源工程学院，湖南 邵阳 422000)

1 研究背景

1.1 水轮机水锤现象产生的机理和危害

水轮机在停机以及事故紧急停机过程中，当压力管道末端的流量发生极速变化时，管道内将出现非恒定流现象，其特点是随着流速的改变压强有较显著的变化，这种现象称为水锤(亦称水击)。水锤现象是各类水力发电机组的共有现象，由于发生水锤时，水锤压力过高，引起阀门和管道破坏，或水锤压力过低，管道因失稳而破坏，从而引起水轮机组的剧烈振动，以及压力钢管的基础位移、剧烈振动和变形[1]。一般当水流平稳地流过压力钢管时，钢管并不会引起振动。但是，若钢管内产生了压力波，如在水轮机处，则由于压力波沿水管的传播会引起钢管的振动。当压力波的振动频率十分接近某段压力钢管的自振频率时，就会引起共振而发生剧烈振动。当压力钢管的共振频率发生改变时，意味着压力钢管的刚度发生改变，必然存在压力钢管连接部位发生松动等缺陷[2-3]。水轮机水锤对压力钢管和机组的破坏极其严重，甚至对电站厂房的安全造成危害。

水锤现象主要发生在水轮机运行的以下过程中：①事故紧急停机过程，即运行中的水力动力突然中断时停机过程。②正常开机、停机、启闭阀门时，尤其在迅速操作、水流速度发生急剧变化的情况。

在本文中，以安装在压力钢管附近的非接触式微波雷达测振系统为基础，利用其多点同步测量的特征，同步测量压力钢管进水阀前后的多点位的振动、位移实时信号，通过对实时数据的自动化分析检测，实现对压力钢管在水锤作用下的实时在线评价。

1.2 传统压力钢管动态形变状态分析评价方法

目前，针对水力机组压力钢管振动形变监测分析主要通过振动在线测量监测系统实现，并未有专门针对水锤作用下压力钢管的振动、位移及形变的监测技术和分析评价方法。就目前所采用的技术而言，主要存在2种缺陷[4-5]。

1.2.1 测量技术缺陷

目前，针对压力钢管的振动、位移测量主要采用加速度振动传感器、磁电式低频振动传感器、电涡流型非接触位移传感器、激光位移传感器等测量方式，其优缺点如下：

(1)传统形变位移/振动测量方法。①加速度振动传感器(接触式)是通过焊接安装固定在压力钢管上。优点为传感器频响较高，适合测量水锤引起的中高频共振信号。缺点为无法准确测量低频振动信号，无法测量压力钢管的位移形变，多点测量需布设多个传感器。②磁电式低频振动传感器(接触式)也是通过焊接安装固定在压力钢管上。优点为适合测量压力钢管中的低频振动位移信号。缺点为水锤冲击引起传感器本体失稳，导致测量失效，对于0.5 Hz以下频率无法准确测量，无法测量压力钢管的位移和形变，多点测量需布设多个传感器。

(2)电涡流型非接触位移传感器(非接触式)测量方法。安装方式为趋近测点位近距离支架固定安装。优点为精度高，能同时测量到压力钢管的振动和位移形变。缺点为需制作金属安装支架固定位移传感器，易受到钢管支座振动、支座位移的影响，支架自身晃动也带来测量误差，多点测量需布设多个传感器。

(3)激光位移传感器(非接触式)测量方法。安装方式为面对压力钢管测点位一定距离上安装。优点为能同时测量压力钢管振动和位移形变，精度高，能避免钢管支座振动及支座位移影响。缺点为极易受到光线、温度、湿度的影响，多点位测量需布设多个传感器，安装难度较大。

1.2.2 分析评价方法缺陷

目前针对压力钢管振动/形变的状态分析评价方法，主要依据压力钢管的振动信号的峰峰值、有效值等，做出一般性的分析评价，并不结合机组运行工况，针对水锤作用下的压力钢管振动形变做针对性的分析评价。另外，对于水锤作用下引起的共振信号的变化(频率和强度)、水力激振的强度等关键特征的识别与评价，并无考虑。

总之，迫于现有技术在高可靠性及恶劣环境适应性方面存在较大的局限性，迫切需要探索先进的针对压力钢管的形变及振动测量新技术与新方法，也需要探索能全面反应压力钢管振动形变的分析评价技术。

2 微波感知测振技术

2.1 微波测振技术概述

连续波微波雷达通过发射特定频率的电磁波信号并接收回波信号，通过基带信号处理实现目标探测，主要通过时差计算与多普勒频移实现目标距离和速度信息的检测。近些年来，基于微波雷达的微运动感知研究得到了大量关注和进展，但在结构形变与振动测量方面的研究较少。此外，针对大型工程结构的高精度形变与振动监测，常需要同步监测多个测点，需解决多测点精确分辨与振动信息反演、邻近目标耦合干扰和杂波干扰抑制等难题[6]。

针对上述问题，近年来，上海交大团队提出了基于微波感知的多点同步形变及振动测量新方法与技术，通过建立微波多点测振原理和振动信息反演提取方法实现大型结构的非接触式多点同步形变及振动监测，且在户外大型桥梁结构的动态响应监测、航天柔性杆结构的模态测试等项目中得到应用验证[6-7]。

具体到水轮机压力钢管振动形变的测量要求，同样需要解决多测点同步形变振动测量问题，而且需要保证0～400 Hz的频率响应性能。本文将从以上方面讨论微波雷达测振在水机测量上的可用性。

2.2 微波形变与振动测量原理及方法

常规的LFMCW(Linear Frequency-Modulated Cont-inuous Wave)雷达发射线性频率调制的电磁波信号并接收目标反射的回波信号，通过计算回波信号的延迟时间实现距离信息测量。基于微波雷达原理的振动测量系统原理如图1所示。

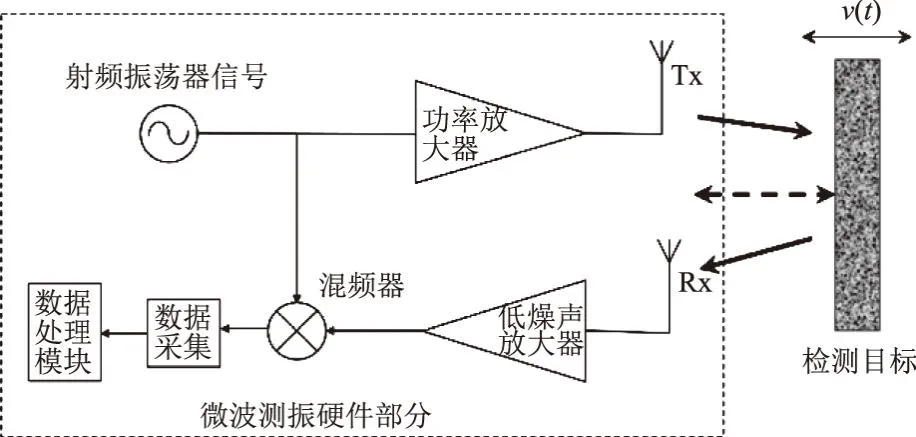
图1 微波测振原理示意

微波测振系统主要由连续波微波雷达、数据采集模块和计算处理计算模块组成。微波雷达用于发射和接收连续微波信号，基于干涉相位调制信息反演振动信息；数据采集模块用于采集雷达基带信号；计算处理计算模块用于雷达控制以及基带信号的处理。典型的连续波微波雷达零差结构由射频振荡器、功率放大器、低噪声信号放大器、功分器、混频器和收发天线等组成。其中CW雷达的射频振荡器产生固定频率的微波信号，LFMCW雷达的射频振荡器产生三角波或锯齿波作为调频波频率调制的微波信号。基于LFMCW雷达的微波振动测量的基本思想为相位干涉测量，相邻时刻目标的振动位移变化Δv为[8-9]

Δv(t)=λΔφ(t)/4π

(1)

式中，Δφ(t)为相邻时刻干涉相位变化；λ为载波波长；t为时间。多扫频周期的LFMCW雷达发射与接收信号瞬时频率如图2所示。

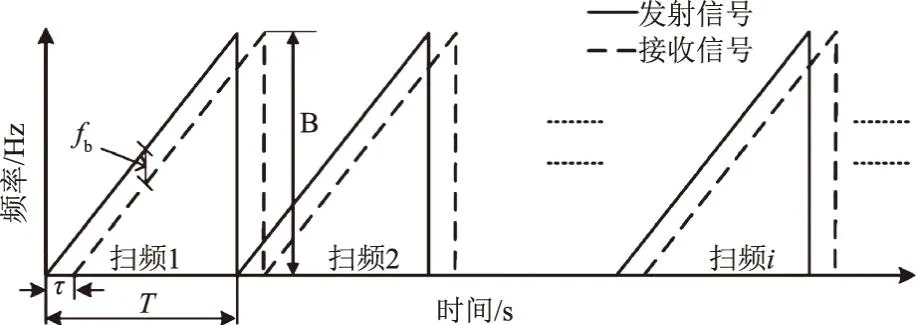
图2 多扫频周期的LFMCW雷达发射与接收信号瞬时频率示意

针对LFMCW 雷达的微波振动测量的原理为跨越多扫频周期的干涉相位演变追踪。考虑到扫频周期往往较短，远小于被测对象的振动频率，在单个扫频周期被测量对象的振动位移可以认为未变化。因此，在第i个扫频周期内，基带的差拍信号为[1-2]

Yb(iT+t)≈Xi(t)Exp[j(2πfbt+φi)]

(2)

fb=2BR0/cT，φi=4πR0/λ0+4πv(iT)/λc

(3)

式中，Xi为第i个扫频周期基带差拍信号的幅值；λ0和λc分别为初始和中心载波频率对应的波长；c为电磁波传播速度；fb为差拍频率；φi和v(iT)分别为第i个扫频周期时间内差拍信号的初始相位和目标振动位移。通过上述信号模型表示和公式推导，可以看出基带信号的干涉相位信息与目标物体的振动位移时域信息成线性关系。因此，通过基带信号的干涉相位演变追踪可以得到相邻扫频周期振动位移时域信息的变化量为[2]

Δv(t)=λcΔφ(t)/(4πcos(φ))

(4)

式中，Δφ(t)和Δv(t)分别为相邻扫频周期基带信号相位信息的变化量和振动位移的变化量；φ为目标振动方向与雷达波束视线的夹角，进而由位移变化量反演目标振动位移时域信息。当毫米波雷达视场范围内存在多个目标时，不同目标反射的回波信号均会被雷达接收，则雷达接收到的多目标分量混叠耦合。因此，第i个扫频周期雷达基带差拍信号可简化表示为

(5)

式中，L为雷达视场范围内可探测的目标分量个数；Xl，i(t)、fl，i、φl，i分别为第l个目标分量在第i个扫频周期的幅值、差拍频率和相位。通过对基带信号进行频谱分析，根据式(3)进行多目标距离的计算分辨，并针对相邻目标分量进行信号解耦分解，最后对各目标分量开展跨越多扫频周期的相位演变追踪，通过式(4)反演计算各目标的振动位移时域信息。

另外，扫频频率和发射带宽(针对FMCW(Frequency-Modulated Continuous Wave)雷达)根据被测对象的固有频率量级与范围等先验知识，选择扫频频率，可设置为被测对象最高分析频率的10～100倍[1]。具体到水轮机压力钢管振动形变的测量要求，可设置扫频频率为4 000 Hz以上，就可以有效保证400 Hz的振动测量频率响应性能[6，10]。另外从测量原理上讲，微波雷达测振技术能够测量超低频振动信号，这一点也是传统磁电式低频振动传感器所无法比拟的。本文采用的微波测振装置技术参数为：测量频率范围0～400 Hz，振动测量精度不低于10 μm，形变位移测量范围1 000 mm内。

3 微波感知测振技术在水轮机水锤效应下压力钢管动态振动形变分析中的应用

3.1 在线测量点位方案

在本方案中，基于微波感知测振技术的在线测量测点位按照如图3、4方式布设。

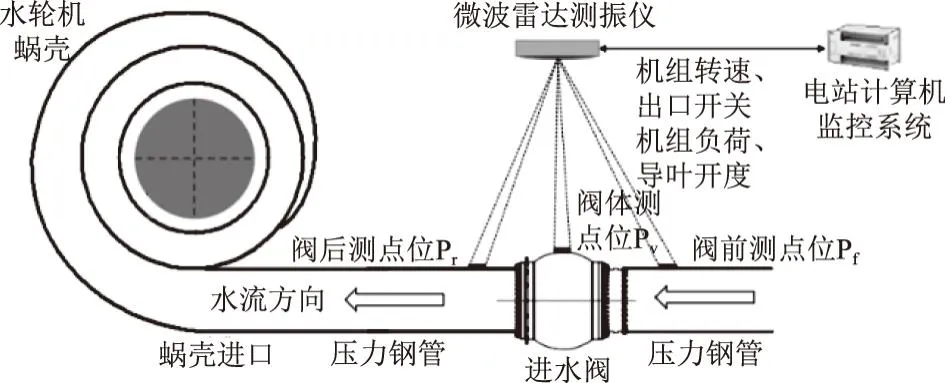
图3 测量点位俯视示意

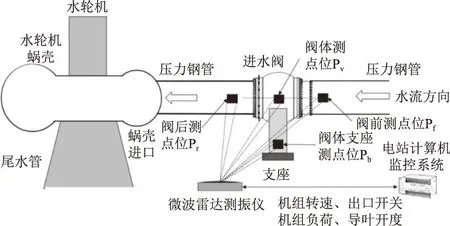
图4 测量点位后视示意

(1)进水阀前振动Pf测点。安装点位为进水阀伸缩节前的压力钢管明管段某断面上，朝向该断面的水平方向，并通过粘贴方式布设一个角反射器，用于增强雷达反射信号。角反射器水平朝向微波雷达测振仪。

(2)进水阀本体振动Pv测点。安装点位为进水阀本体上中心断面上，该测点朝向该断面的水平方向，并通过粘贴方式布设一个角反射器，用于增强雷达反射信号。角反射器水平朝向微波雷达测振仪。

(3)进水阀后振动Pr测点。安装点位为进水阀后的压力钢管明管某断面上，该测点朝向该断面的水平方向，并通过粘贴方式布设一个角反射器，用于增强雷达反射信号。角反射器水平朝向微波雷达测振仪。

(4)压力钢管支座振动Pb测点。安装点位为压力钢管支座上，该测点朝向该断面的水平方向，并通过粘贴方式布设一个角反射器，用于增强雷达反射信号。角反射器水平朝向微波雷达测振仪。

(5)机组转速、发电机出口开关、有功功率测点。安装点位为从电站监控系统通过数据通讯方式引入。

3.2 压力钢管在线振动形变状态分析

在本文中，微波雷达测振仪的内部计算处理模块实时连续同步采集上述4个测点的原始振动、位移波形信号，并从监控系统实时读取机组转速、发电机出口开关、机组有功功率信号，根据本文提出的分析评价方法实现对水锤作用下对压力钢管振动、形变的评价。由于水锤效应主要出现在机组开停机以及事故紧急停机过程中，尤其以事故紧急停机过程尤为关键，因此在本文重点研究微波雷达振动测量技术在事故紧急停机过程的数据采集和状态分析评价方法。

正如上文分析，水锤效应会引起钢管支座位移、钢管形变和振动等多种特征的变化，因此对压力钢管在水锤作用下的状态分析需要从支座位移、钢管形变和振动等多个方面去分析。

3.2.1 事故紧急停机过程数据的在线采集

设fs为微波雷达测振装置的采集频率，ΔTs为采集周期，ΔTs=1/fs。首先，持续采集机组转速、发电机出口开关、功率信号，记为xr/min(i)、xsw(i)、xpower(i)，i为采样点。记Rr为机组的额定转速，Pr为机组额定有功功率。那么从xsw(ik0)=1且xsw(ik0+1)=0，满足条件0.995Rr≤xr/min(ik0)≤1.005Rr且xpower(ik0)≥0.05Pr(即机组进入事故停机过程)时刻开始，连续同步采集多点位振动信号，存储到vpf(i)、vpv(i)、vpr(i)、vpb(i)时间序列中，并同步记录转速信号xr/min(t)，直到满足条件xr/min(i)≤0.01Rr时，停止采集。其中vpf(i)、vpv(i)、vpr(i)、vpb(i)分别为进水阀前测点、进水阀本体点、进水阀后测点、压力钢管基础支座的振动波形时间序列。

3.2.2 压力钢管基础位移和形变特征分析

由于本文所描述的微波雷达测振技术具有同步测量多点位的能力，其多点位的振动信号通过同一套采集和计算处理模块获得，因此多点位信号在频率特性、增益特性以及同步性上具有良好的一致性，故而利用同一套微波雷达测振系统测量得到的多点位之间的数据比较是可行的。在本文中，利用微波雷达测振这一特性对压力钢管的基础位移和形变特征进行分析。具体方法为：以1 s时长为单位，分段截取vpf(i)、vpv(i)、vpr(i)、vpb(i)的原始振动时间序列信号，并计算进水阀前测点、进水阀本体测点、进水阀后测点、压力钢管基础支座测点每一段时间振动信号的平均值形成新的时间序列Apf(j)、Apv(j)、Apr(j)、Apb(j)。以过程起始时刻测值为基准点，计算全过程相对于支座的形变/位移时间序列，并计算过程最大基础位移和形变特征，计算方法为

Dp_base=max(Apb(j)-Apb(0))

(6)

Df_pf=max((Apf(j)-Apb(j))-(Apf(0)-Apb(0)))

(7)

Df_pr=max((Apr(j)-Apb(j))-(Apr(0)-Apb(0)))

(8)

Df_pv=max((Apv(j)-Apb(j))-(Apv(0)-Apb(0)))

(9)

式中，j=0，…，n；n为全过程平均位移数据序列的总数量；Dp_base为压力钢管基础位移；Df_pf为进水阀前压力钢管最大形变；Df_pv为进水阀本体最大形变；Df_pr为进水阀后压力钢管最大形变。

3.2.3 压力钢管振动状态特征的分析

在事故紧急停机过程，由于流量的减小导致输入水流力矩减小，同时转轮入口水流速度减小进而导致水泵水轮机偏离最优工况点，并引起过流部件内压力脉动的急剧上升变化，从而引起压力钢管和进水阀的振动。主要的振动成分包括[11-12]：

(1)转轮叶片通过频率振动及其二阶频率振动，测试表明该频率振动是水锤作用下，压力钢管的主要振动频率，尤其是二阶频率振动[10]。该振动信号的振动频率与机组转速成正比关系，即

flb(t)=lNbfr(t)=lNbxr/min(t)/60 (l=1，2)

(10)

式中，flb(t)为转轮叶片通过频率振动的瞬时频率；l为阶数，通常只取1、2倍；Nb为机组转轮叶片数，这是个固定的数值；在停机过程、事故紧急停机过程，机组转速是时变信号，因而该振动信号也是时变信号。

(2)水锤作用下引起的压力钢管、进水阀的共振、水力激振，其振动频率与机组转速无关[13]。

(3)其他由于压力脉动引起的振动，其特征是振动幅值、相位不稳定，具有一定的随机性。

(4)其他频率振动，如机组转速频率等。

在压力钢管状态评价中，需要对上述多种振动信号进行特征识别提取。本文重点讨论转轮叶片通过频率振动及其二阶频率振动以及共振、水力激振频率特征的分析与提取方法。

3.2.3.1 转轮叶片通过频率振动及其分量的分析提取

由于微波雷达测量到的振动信号中并不包含转速键相信号，直接采用原始振动信号通过傅里叶变换或者短时傅里叶变换提取时变的叶片频率及其二阶频率进行提取会产生较大误差，因此，本文提出了采用基于转速估计的变频率重采样方法，实现对叶片频率及其二阶频率幅值较为精确的分析提取，当然该方法也可以应用于变转速过程转频振动等其他与转速相关的振动频率提取与分析。具体如下：

(1)基于分段多项式的机组转速估计。图5为某机组事故紧急停机过程转速变化，可以看出，在事故紧急停机过程中，首先从tt0时刻开始，机组转速急剧上升，达到最高转速之后开始单调下降，直至停机。在本文中，采用分段式多项式来逼近机组转速的变化函数

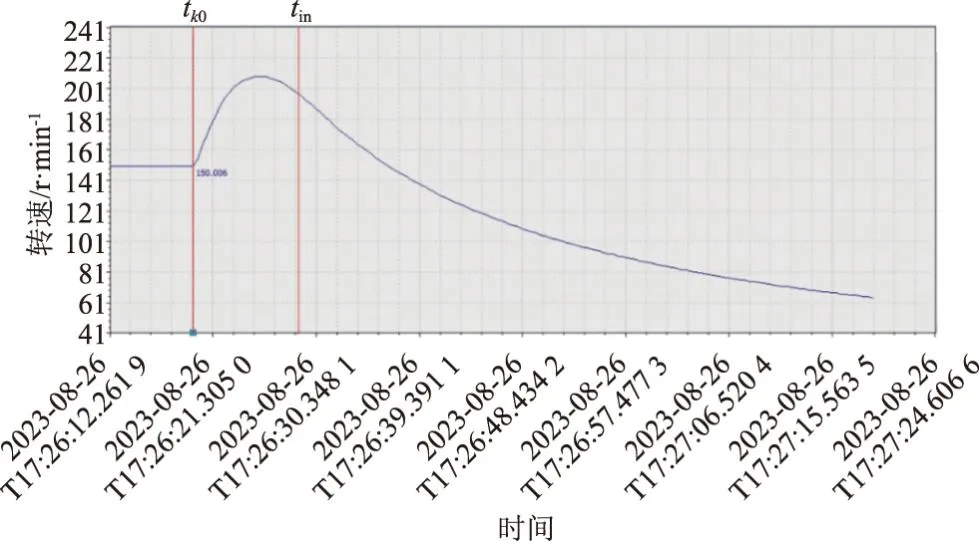
图5 某机组事故紧急停机过程的转速变化曲线

yr(t)=c0+c1t+c2t2t≥0且t≤tin-tk0

(11)

yr(t)=k0+k1t+k2t2+k3t3t≥tin-tk0

(12)

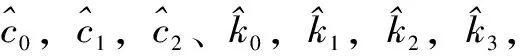
(13)

(14)

(3)对上述vpf(j)、vpv(j)、vpr(j)、vpb(j)时间序列做快速傅里叶变换，计算获得各部位振动测点较为精确的转轮叶片通过频率振动幅值及其二阶振动频率幅值。

3.2.3.2 压力钢管共振及水力激振频率分量的分析提取

当水锤产生后，在水锤的短时冲击作用下，可能引起钢管、进水阀的短时共振，该振动频率与钢管和进水阀的刚度、结构有关，与机组转速无关。另外，压力钢管中的水力激振频率也与转速无关[13-14]。当水锤的冲击作用消失之后，共振信号也逐渐衰减消失。而对共振信号特征的识别提取的目的是为用以识别压力钢管、进水阀本体的刚度变化，进而评价压力钢管、进水阀本体是否产生结构缺陷。在本文中，采用分段频域叠加平均滤波方法，识别共振频率以及水力激振频率并对其幅值进行提取[15]。以进水阀前振动测点为例，具体为：从事故紧急停机过程开始，以Δτ(比如0.5 s)时长为单位，从vpf(i)的原始振动时间序列信号中截取M段时间序列(每组时间序列时长为Δτ)vpf(j0)，…，vpf(jM-1)。分别对上述M组时间序列数据vpf(j0)，…，vpf(jM-1)做FFT变换获得频域数据[Rpf_j0(ω)，Ipf_j0(ω)]，…，[Rpf_jM-1(ω)，Ipf_jM-1(ω)]。其中Rpf_j0(ω)，…，Rpf_jM-1(ω)为M组数据对应的频域实部数据，Ipf_j0(ω)，…，Ipf_jM-1(ω)为虚部数据。对上述M组实部和虚部分别做累加平均

(15)

(16)

对上述归一化处理

(17)

那么rpf_j0_M-1(ω)就是M组连续振动序列经过频谱分段累加平均滤波后获得归一化函数的频域数据。其每个频率对应的幅值，反应了在这M段振动信号中对应频率重复出现的时间相关性。如果该幅值趋近于1.0，那么提示该频率信号重复出现；如果趋近于0，则说明，该频率的信号并不是重复出现的周期信号。经过多叠加重滤波之后，频率稳定的周期性信号会被增强，而频率变化或者随机振动信号，则会被抑制或削弱。具体来说，由于转轮叶片通过频率振动及其二阶频率振动频率是个与转速相关的时变频率，以及一定随机性的压力脉动引起的振动将会在rpf_j0_M-1(ω)中削弱，而不随转速变化的共振信号或者水力激振的信号被增强。M组数越大，对共振信号的增强效果越好。

从rpf_j0_M-1(ω)查找|rpf_j0_M-1(ω)|趋近于1.0的频率，该频率就是该测点位的共振频率或者水力激振频率。对vpf(j0)…vpf(jM-1)分别采用FFT计算其频域幅值数据，并计算共振频率对应的振动幅值，并从其中计算最大值，则对应该过程共振频率的幅值。

采用相同方法，计算进水阀本体测点共振频率及共振幅值及进水阀本后压力钢管测点共振频率及共振幅值。

3.2.3.3 其他振动特征参数的提取

其他振动特征参数包括振动信号峰峰值、振动信号有效值、振动信号峭度值和振动信号偏度值等，在本文中不再赘述。

4 测试案例分析

4.1 实验室对比测试

为了验证微波振动测量技术和准确性和有效性，在实验室激振器台面上布设磁电式低频振动传感器以及电涡流传感器测量振动。同时在激振器台面上布设角反射器，微波振动雷达同步测量激振器台面振动。给定不同频率下的正弦波信作为激励信号，驱动激振器做单一频率的振动，波形如图6所示。

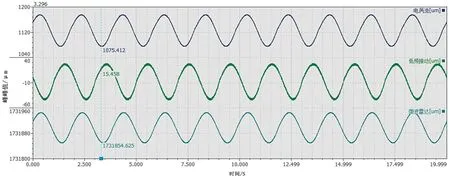
图6 对激振器台架上单一频率振动不同测量方式测量获得的振动波形

对上述3种测试方法同步测试并计算振动峰峰值，测试结果对比如表3所示。

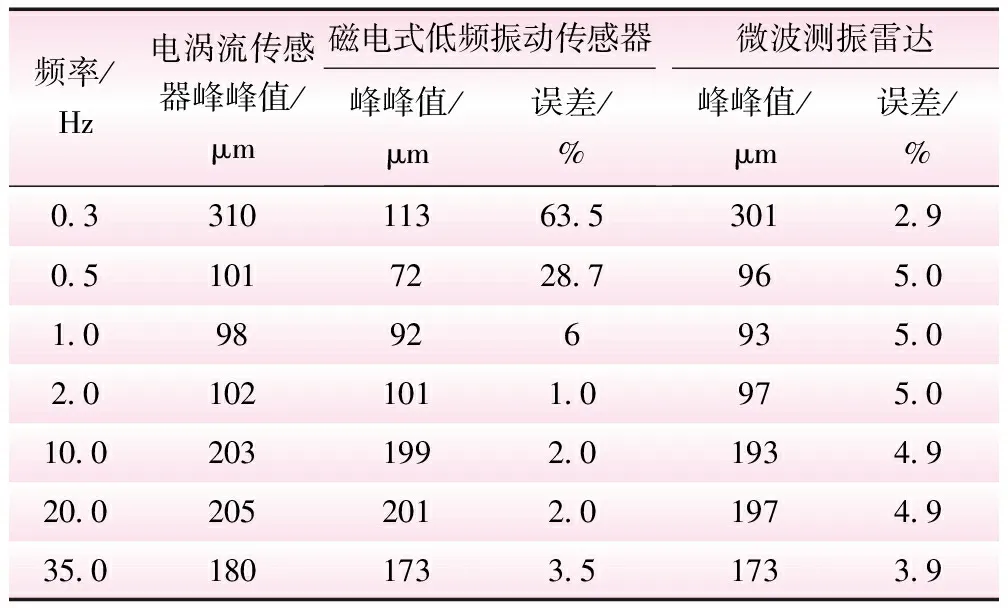
表3 不同频率振动下不同传感器测量峰峰值对比

从表3中可以看出，微波测振雷达测量结果与电涡流测量的峰峰值误差不超过5.0%；另外，对于0.3 Hz的低频振动信号，微波雷达测振的误差仅为2.9%；而对照磁电式传感器，该传感器对于0.3 Hz的低频振动信号测量误差达到了63.5%，从而也证明了微波测振雷达良好的超低频测量性能。

4.2 机组测试数据分析

4.2.1 转轮叶片振动状态特征通过频率振动分量及其倍频的分析提取

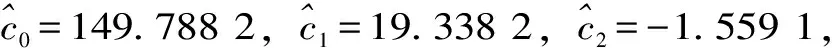
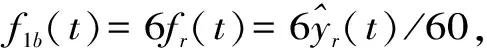
图7 某机组事故紧急停机过程进水阀后振动信号未经重采样的频谱

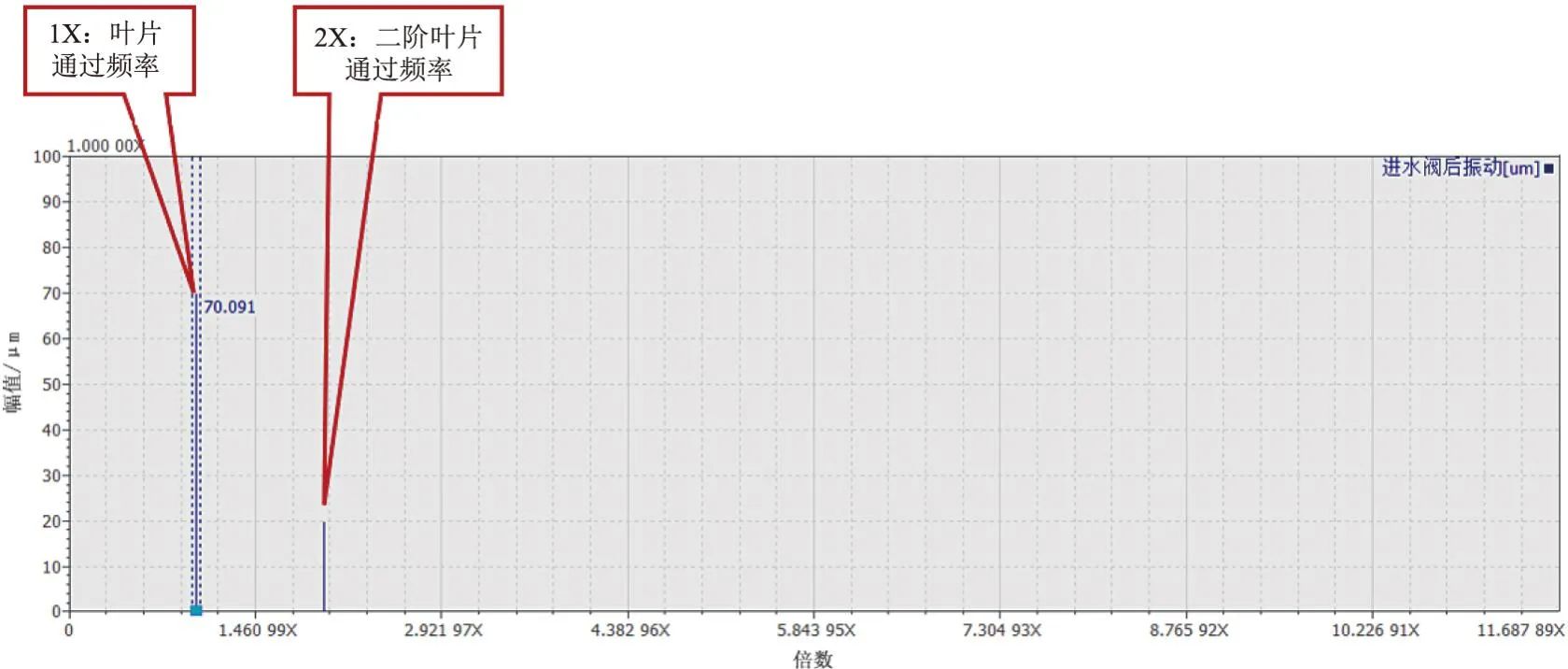
图8 某机组事故紧急停机过程进水阀后振动信号经重采样的频谱

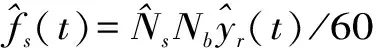
表4为不同方式计算频率特征值对比，可以看出，直接采用原始定时采样数据计算频率幅值与重采样数据计算频率幅值相比有较大误差，采用转速跟踪重采样方法能提高相关特征频率的计算精度。

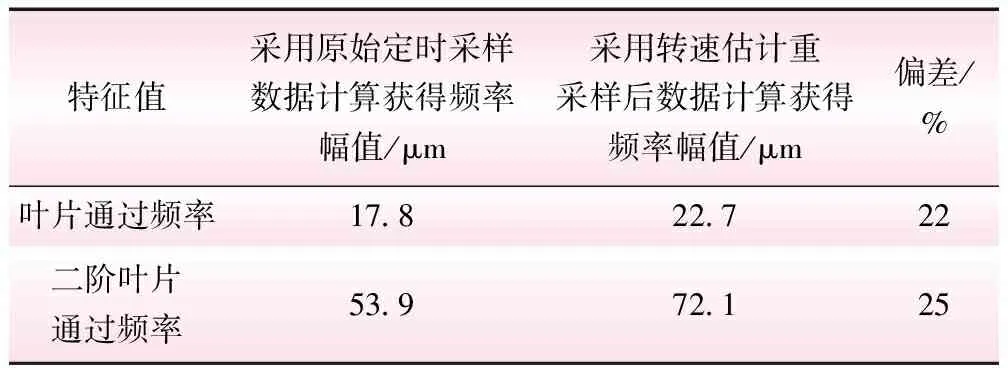
表4 不同方式计算频率特征值对比

4.2.2 压力钢管共振及水力激振频率分量的分析提取

图9为某机组事故紧急停机转速变化过程中进水阀后压力钢管振动测点的振动信号时间分段频谱。从图9可以看出，在该过程中，机组转速从150 r/min上升到207 r/min。从频谱中可以看出，信号中包含了叶片通过频率(16～22 Hz之间)、二阶叶片通过频率(优势频率)、20 Hz以上的压力脉动引起的振动信号、在75～80 Hz之间的固定频率成分，该频率应为共振频率或者水力激振频率，其频率幅值甚至小于二阶叶片通过频率的幅值。经采用本文提出的频谱分段累加平均滤波(Δτ设定为0.5 s，M设定为16)之后，其归一化频谱如图10所示。

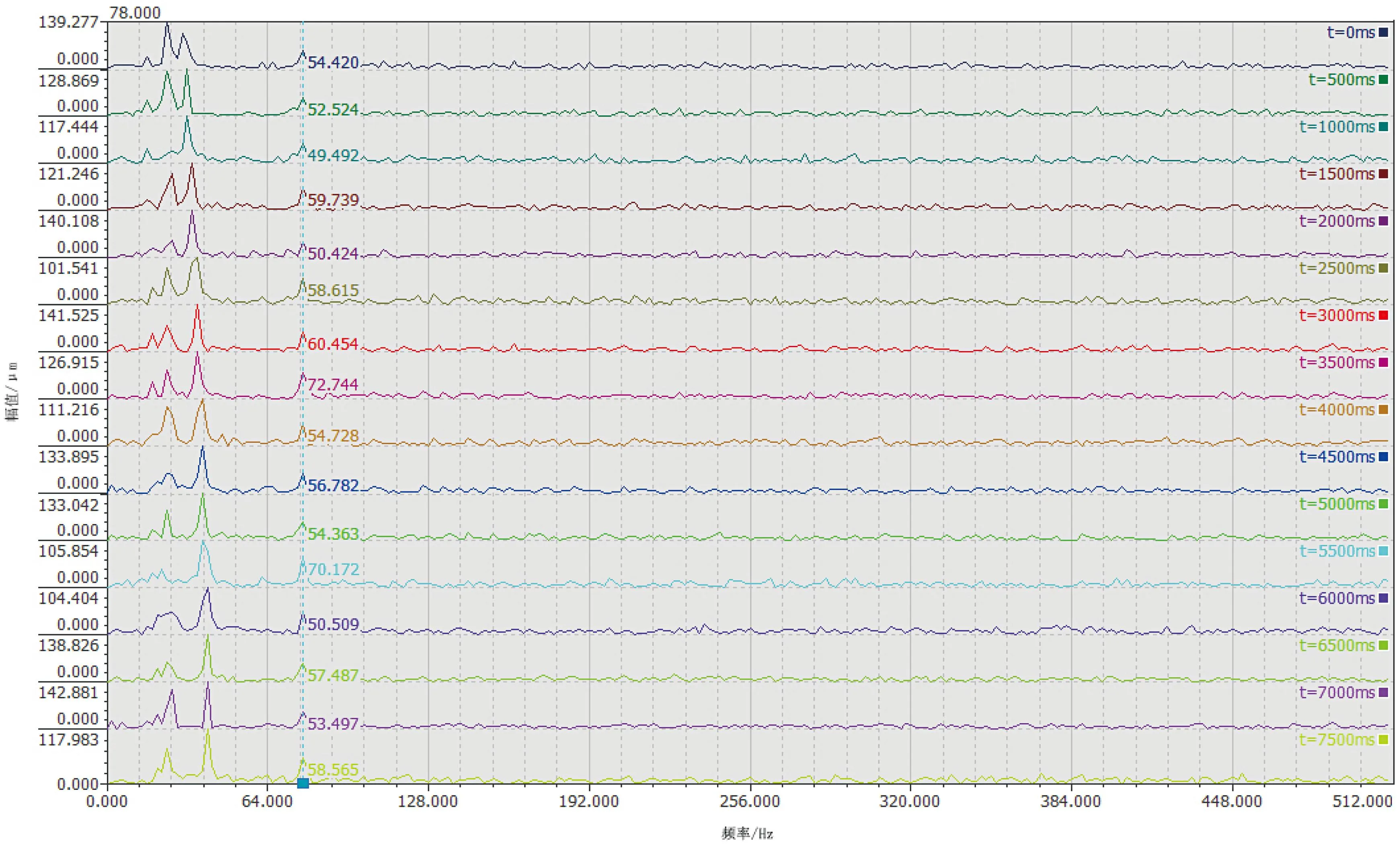
图9 紧急事故过程的转速变化过程中进水阀后压力钢管振动分段频谱

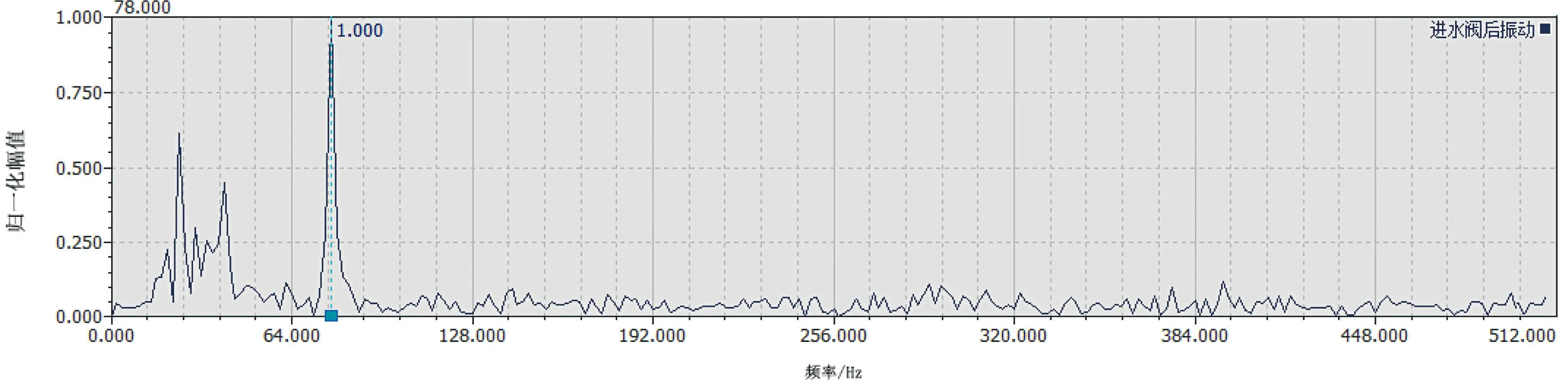
图10 分段累加平均后滤波后的归一化频谱

从图10中可以看出，75～80 Hz之间的共振频率被增强了，其归一化幅值为1.0，而叶片通过频率(16～22 Hz之间)则被抑制到0.6左右，其二阶频率则被削弱到0.5以下。其他的频率成分则被抑制到0.1以下。由此，识别出该机组在事故停机转速上升过程中存在约78 Hz的不随转速变化的振动频率成分，该振动应该为压力钢管的共振频率或为水力激振频率。再从原始进水阀后压力钢管振动信号经FFT分解，计算78 Hz频率对应的最大幅值约为70 μm，从而准确提取到过程中压力钢管的共振频率或水力激振频率。通过持续监测该特征的频率变化和幅值变化，则可用于评价压力钢管、阀体的松动、刚度变化等缺陷。

5 结 语

本文研究了微波感知测振技术及其在水轮机水锤作用下压力钢管的振动形变状态评价方面的应用，并通过实际测试数据的对比分析证明了该方法的有效性和实用价值。从实际意义来说，基于微波感知测振技术具有多点位同步测量、非接触式测量、幅值精度较高、能同时测量形变位移和微振动的特点，而且能适应温度变化较大、湿度较高等恶劣环境下振动的测量。具体到微波雷达测振技术在压力钢管状态测量分析评价应用，本文也提出了基于转速估计变频率重采样方法的叶片通过频率等振动倍频提取技术和基于频谱累加平均滤波方法提取共振、水力激振等频率特征的方法，用以提高压力钢管振动特征参数的准确性和有效性，从另外一个侧面，验证了微波测振技术的频率特性在水电机组压力钢管振动形变测量的适应性。