一种超参数自适应航天器交会变轨策略优化方法

孙雷翔，郭延宁，邓武东，吕跃勇，马广富

（1.哈尔滨工业大学（深圳）空间科学与应用技术研究院，深圳 518055；2.哈尔滨工业大学航天学院，哈尔滨 150001；3.上海卫星工程研究所，上海 201109）

0 引言

随着航天技术的不断发展，太空中航天器的数量快速增加，地球同步轨道（GEO）等特殊轨道逐渐变得拥挤。根据美国忧思科学家联盟（UCS）卫星数据库统计，截至2022 年12 月31 日，在地球同步轨道上已有580颗有效航天器［1］，多数为通信卫星等高价值目标。与近地轨道相比，轨道高度更高的GEO 航天器具有发射成本高、运营年限长等特点，对2008—2010 年GEO 航天器失效数量的统计［2］表明，燃料耗尽失效比例已经达到85.4%。针对GEO航天器等高价值目标进行燃料加注、故障维修等在轨服务（OOS）可以延长航天器在轨年限、降低航天器运营成本，具有十分重要的意义［3］。其中，航天器交会技术是实现在轨服务的关键技术之一。只有在完成交会后，才能进行接管控制、在轨加注、故障维修等在轨服务。在进行在轨服务之前，选择适当的转移策略可以最大程度地节省服务航天器的燃料消耗，为后续服务保留更多的机动能力，延长其服役时间。

目前在轨航天器主要变轨方式为脉冲变轨，其发动机点火时间很短，可近似为瞬间完成，具有速度改变而空间位置不变的特点。根据脉冲变轨次数的不同，又分为多脉冲变轨和双脉冲变轨。多脉冲变轨中使用较多的是三脉冲变轨，主要包括双椭圆变轨和三脉冲Lambert 变轨。其中双椭圆变轨虽然计算相对简便，但难以灵活地调整入轨相位，且难以满足部分在轨服务任务的时限要求；三脉冲Lambert变轨相比于双脉冲变轨决策变量维度大幅上升，计算难度增大，且使用三脉冲Lambert 变轨完成交会任务的规划研究往往基于近距离假设（100 km以内）使用CW 方程，时间约束为固定量或自由量［4］，而本文主要面向远距离交会问题的快速规划，且时间约束为不等式形式。综合考虑现有研究进展和计算的快速性，本文选择双脉冲变轨方式。双脉冲变轨中，Hohmann 变轨被证实为双脉冲共面变轨中燃料消耗最小的方法［5］，但其难以调整目标位置和转移时长；Lambert 变轨不受半长轴、倾角等轨道根数限制，几乎可以实现任意转移时长到达任意位置，因其灵活性在轨道优化问题研究中被广泛应用，但其燃料消耗往往较大，只有适合的变轨策略才能使其具有实际应用价值。

为在不同的轨道转移条件下寻找最优化Lambert 变轨策略，针对其高复杂度、强非线性、非凸的特点，许多学者结合智能优化算法提出了不同的规划方法，包括遗传算法［6-7］、模拟退火算法［8］、粒子群优化算法（Particle swarm optimization，PSO）等，其中PSO 因原理简单直观被广泛应用［9-12］。Pontani等［9-10］率先将PSO 应用于空间轨迹优化问题和脉冲转移轨道的优化求解中；陈全等［11］以变轨时刻和真近点角作为决策变量，利用PSO 进行多脉冲燃料最优Lambert 转移轨道的求解，Yang 等［12］利用量子行为粒子群优化和序列二次规划相结合的混合算法对航天器远距离快速协同交会过程进行了优化求解，非共面协同交会的仿真结果证明，相比于其他算法，该算法在收敛速度和解的稳定性方面均有一定优势。

虽然PSO 具有全局搜索能力，但不佳的超参数选择（包括惯性因子、学习因子）往往会导致收敛速度与全局最优性相冲突，例如：①过小的惯性因子会导致PSO 全局搜索能力较差，容易陷入局部最优；②过大的惯性因子会导致PSO 局部搜索能力较差，粒子容易在最优位置附近产生振荡而不是收敛到最优位置；③过小的个体学习因子或过大的群体学习因子会导致PSO 的“无私行为”，即个体极大程度地服从于群体，粒子向群体最优位置快速靠拢，迅速丧失种群的多样性，容易产生早熟现象；④过小的群体学习因子或过大的个体学习因子会导致PSO 忽略群体共享信息，收敛速度过慢。PSO 及其现有相关改进算法中的超参数通常是人为给定常数或在迭代过程中根据固定规则简单调整的，缺乏自学习、自适应能力。为了弥补这一缺陷，将强化学习与PSO 相结合的思想逐渐受到关注。目前，大多数结合强化学习思想的PSO都是基于Q学习的自适应算法，将搜索最优解的优化过程视为寻找最优策略以获得最大期望回报的强化学习过程。Samma等［13］提出了一种新的基于强化学习的记忆粒子群优化模型，每个粒子根据强化学习算法生成的动作进行5 类操作，包括探索、收敛、高跳、低跳和微调。Hsieh等［14］提出了一种基于Q学习的群优化算法，根据个体累积的表现而不是每次评估时的瞬时表现来选择最佳的粒子。Liu等［15］使用Q学习思想，以与全局最优粒子的距离和粒子适应度排名作为输入，根据当前优化进度确定奖励函数，在单目标优化测试问题和多目标优化测试问题中都取得了不俗的表现。Xu 等［16］提出了一种结合拓扑结构的强化学习粒子群优化算法，根据粒子群的多样性和上一步的拓扑结构从Q 表中选择最佳的拓扑。Lu 等［17］通过选择粒子群算法迭代过程中的精英粒子并学习其搜索行为，构建了精英行为网络，有效降低了污水处理的能量消耗。不同于上述研究局限于传统Q学习得到的离散Q 表（算法超参数只能在给定离散数值中进行选择），Yin 等［18］利用一个深度强化学习网络控制PSO 中的超参数变化，实验结果表明该算法优于几种最先进的PSO 变体。可以看出，与传统优化算法相比，结合强化学习的PSO 可以有效地利用历史数据，不仅能根据自身经验进行学习，还能交换信息进行学习。强化学习已广泛应用于包括航天器在轨博弈在内的宇航智能化研究中，如耿远卓等［19］针对脉冲推力航天器轨道追逃博弈问题，提出一种基于强化学习的决策方法，实现追踪星在指定时刻抵近至逃逸星的特定区域。但结合强化学习思想的PSO 在空间轨道变轨策略优化中应用还较为少见。

除在合适的超参数选择方面进行研究外，部分学者还致力于通过改进算法模型来避免PSO陷入局部最优。综合学习粒子群优化算法（Comprehensive learning particle swarm optimization，CLPSO）由Liang等［20］在2006 年首次提出，旨在避免PSO 陷入局部最优。该算法利用所有其他粒子的个体最优解来更新粒子的速度，以保留群体的多样性，防止过早收敛。CLPSO 已成功应用于多智能体路径规划［21］、结构可靠性优化设计［22］等诸多领域中，均取得了不俗的应用效果。CLPSO 较好地避免了算法陷入局部最优，但这是以牺牲收敛速度为代价的。在此基础上，文献［23］提出了改进式综合学习粒子群优化算法（Improved comprehensive learning particle swarm optimization，ICLPSO）。相比于CLPSO 仅利用其他个体最优信息，ICLPSO 额外利用了全局和个体最优信息，同时采用多种群设计，各种群超参数相互独立，在保持粒子多样性的情况下加快了收敛速度。

因此，为解决GEO 航天器交会Lambert 变轨策略优化问题，在保证求解准确性的同时兼顾计算快速性的需求，本文引入ICLPSO，并将之与深度强化学习网络相结合，组成可根据粒子群收敛情况实时调整超参数的强化学习粒子群算法（Reinforced learning particle swarm optimization，RLPSO），将该算法用于上述优化问题中，实现算法超参数根据实时迭代收敛情况的自适应动态调整，在避免陷入局部最优解的同时减少迭代次数，降低计算负荷，以实现快速、准确求解。

本文所提算法总体架构如图1所示。

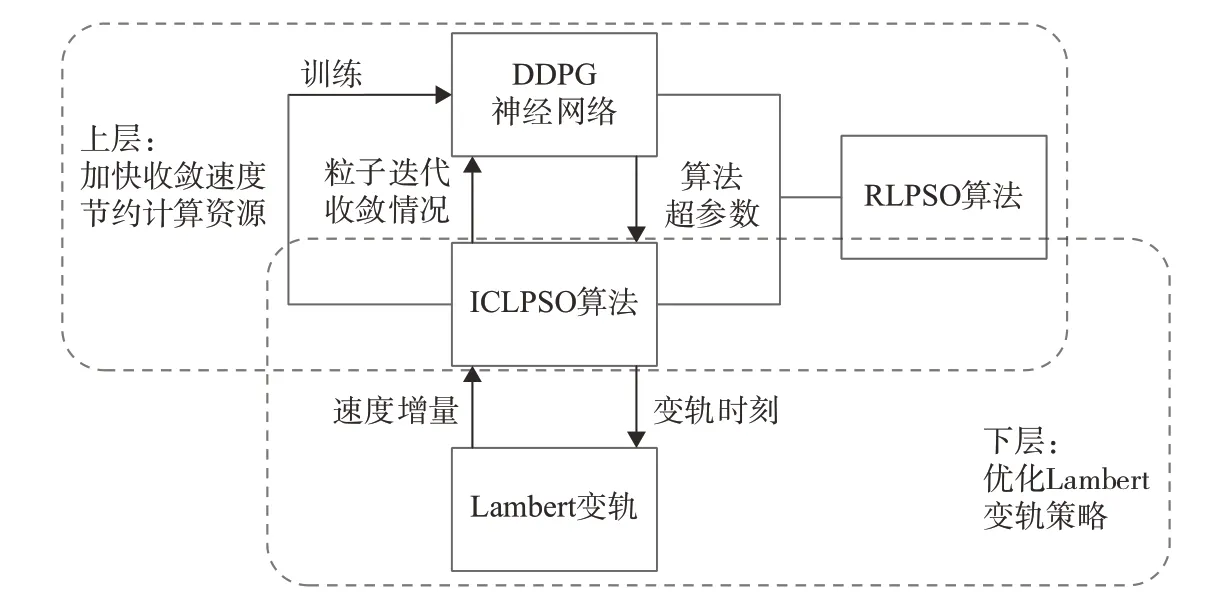
图1 本文所提算法总体架构Fig.1 Overall architecture of the proposed algorithm

1 GEO航天器交会Lambert变轨模型

为便于描述交会过程，定义以下参数变量：

Ttotal：航天器交会任务时长上限，即交会任务必须在该时长内完成。

T：服务航天器相对初始时刻（定义为0 时刻）的脉冲机动时刻，T=[T1T2]。T1为服务航天器第1 次脉冲机动时刻，T2为服务航天器第2 次脉冲机动时刻，转移时长可表示为Δt=T2-T1。

S：服务/目标航天器状态矢量[rTvT]T=[rxryrzvxvyvz]T，r和v分别代表航天器在地心惯性坐标系下的位置和速度，rx，ry和rz则对应r在地心惯性坐标系下的三轴分量，vx，vy和vz对应v在地心惯性坐标系下的三轴分量。s/t 代表航天器为服务/目标航天器，Ti代表状态矢量对应的时刻。

ΔV：描述服务航天器轨道转移时的脉冲矢量，为第1 次机动时的脉冲矢量，Δv2为第2次机动时的脉冲矢量。

依托上述参数，本文所述GEO 航天器交会过程可按时间顺序分为以下步骤：

1）0 时刻至T1时刻，服务航天器在其初始轨道上运行。

2）T1时刻，服务航天器施加第1 次Lambert 变轨脉冲，进入转移轨道，脉冲矢量为Δv1。

3）T1时刻至T2时刻，服务航天器在转移轨道上运行。

4）T2时刻，服务航天器施加第2 次Lambert 变轨脉冲，进入目标轨道完成交会，脉冲矢量为Δv2。

5）在交会过程中目标航天器不进行变轨。

本文的目标为选取合适的两次脉冲变轨时刻T1和T2，使得燃料消耗最优化，也即之和最小。GEO航天器交会过程如图2所示。

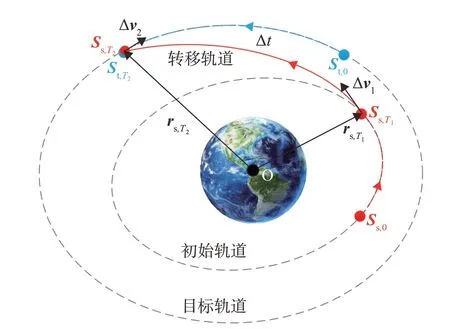
图2 GEO航天器交会过程Fig.2 Rendezvous process of spacecraft in GEO

1.1 基本假设

针对GEO 目标航天器，将服务航天器部署在相近的GEO 轨道上，相较于LEO 轨道部署方案及地面应急发射方案，燃耗更低且响应更快［24］。本文基于上述在轨服务模式，作出如下基本假设：

1）本文着重研究服务航天器轨道转移策略，对于在轨服务过程中的姿态控制不作具体展开。

2）服务/目标航天器的轨道根数应选取高度与地球静止轨道相近的小倾角、小偏心率轨道。

1.2 交会模型建立

基于上述假设，可以定义航天器交会模型，包括轨道动力学模型、末态约束、轨道转移方法、目标函数、优化变量和时间约束。

1）轨道动力学模型

对于GEO 轨道上较短时间的轨道转移过程，考虑J2摄动的轨道动力学模型即可满足大部分工程的精度要求，因此本文轨道转移仿真部分采用考虑J2摄动的轨道动力学模型如下：

式中：μ为地球引力常量；aNSP为地球非球形引力加速度，其计算公式如下：

式中：J2为非球形参数；Re为地球半径。

考虑到交会任务优化需进行多次迭代，同时本文所提算法又涉及到对深度神经网络的训练，为保证计算速度，本文神经网络训练及优化求解部分采用仅考虑地球引力的二体模型。

2）末态约束

为完成交会，在轨道转移的末时刻，服务航天器与目标航天器的位置、速度应保持一致。因此，通过轨道动力学递推得到的目标航天器末状态即为服务航天器最终期望状态。

3）轨道转移方法

本文采用Lambert 转移，通过轨道动力学递推可以获得变轨前服务航天器的状态和目标航天器的末状态，也即服务航天器最终期望状态Lambert变轨过程可表述为［25］：

进一步可以得到两次转移的脉冲矢量：

4）目标函数

以航天器交会任务消耗燃料最优为目标，将两次脉冲的速度增量之和作为目标函数：

5）优化变量

目标函数与Lambert 变轨的两次脉冲有关，而在两航天器初始轨道根数确定的情况下，两次脉冲又只与机动时刻有关，选取T=[T1T2]作为优化变量，通过调整T的取值使得目标函数取得最优值时，即可相应得到两次脉冲的大小及方向，进而确定完整交会策略。

6）时间约束

优化变量各分量要满足合理性，即第1次脉冲、第2 次脉冲要依次进行，且交会要在时长上限内完成，具有以下约束：

2 用于交会变轨策略优化的ICLPSO算法简介

2.1 粒子适应度函数

适应度函数表征了当前粒子对应的解的优劣。本文以燃料消耗最小为优化标准，选取前文1.2 小节中的目标函数J作为适应度函数，J的取值与当前粒子位置Xi、服务星初始状态Ss，0、目标星初始状态St，0有关，第i个粒子的适应度函数可表示为如下形式：

2.2 PSO简介

在PSO的迭代中，每个粒子位置、速度的更新与全局最优位置Gbest和个体最优位置Pbest相关。第i个粒子的更新公式如下：

式中：Xi=[xi1xi2…xiD]T为第i个粒子的位置；D为种群维度，粒子位置的各分量取值要满足区间[xmin，xmax]；Vi=[vi1vi2…viD]T为第i个粒子的运动速度；w为惯性因子；c1和c2为学习因子；w、c1和c2均为人为给定常系数；rra_1和rra_2为［0，1］区间内取值的随机数。算法持续迭代，直至触碰收敛迭代次数上限gcmax或迭代次数上限gemax时算法结束，输出全局最优位置Gbest作为最终优化结果。

2.3 CLPSO简介

CLPSO［20］在PSO 的基础上修改了粒子更新机制，不再跟随全局最优位置与个体最优位置，转而对每个粒子随机给定种群内通过锦标赛规则筛选出的优胜粒子，并定期更新该粒子，将该粒子的个体最优位置与当前粒子的个体最优位置依维度按概率进行交叉，作为当前粒子真正的跟随目标。第i个粒子运动速度各分量更新公式如下

式中：上角标d表示第d维度的分量，fi=[fi(1)，fi(2)，...，fi(D)]表示第i个粒子追随的优胜粒子群，通过锦标赛规则产生，即：随机抽取种群中2 个其他粒子，对比它们的个体最优值，择其中较优者作为优胜粒子，重复该过程直至产生足量的优胜粒子；rra和P为［0，1］区间内取值的随机数；Pci为第i个粒子的交叉概率，服从以下公式：

式中：a=0.05，b=0.45 为常系数。当当前粒子的个体最优值持续m代未更新时，则重新选择优胜粒子群（除去自身及上一轮选中的粒子）。

CLPSO 算法整合了种群内全体粒子的历史信息，挑选出更有优化可能的方向更新粒子，避免陷入局部最优解，但也因粒子运动方向相比传统粒子群算法更为分散导致其收敛速度慢于后者。

2.4 ICLPSO算法简介

为在较快收敛速度的基础上兼顾全局最优性，在PSO 的基础上结合CLPSO 中的优胜粒子跟随机制，文献［23］提出了ICLPSO，该算法中第i个粒子运动速度各分量更新公式如下：

同时，出于搜索的灵活性考虑，将粒子群种群均匀划分成多个子种群，每个子种群使用独立的惯性因子w、学习因子c1，c2和c3，需要指出的是，每个子种群的上述4种超参数均为后续利用强化学习进行自适应优化的超参数。

ICLPSO算法流程如下：

算法1.改进式综合学习粒子群算法

1）初始化粒子群；

2）使用式（8）计算粒子适应度，并分别记录全局最优和个体最优；

3）如当前粒子个体最优值停滞超过m代未更新，则通过锦标赛规则更新优胜粒子群；

4）使用式（12）更新粒子群；

5）更新收敛迭代次数和迭代次数，如触碰收敛迭代次数上限gcmax或迭代次数上限gemax则算法结束并输出最优解，否则返回2）继续迭代。

3 基于强化学习的ICLPSO超参数调整策略设计

本节以前文2.4 小节介绍的ICLPSO 为基底，设计基于强化学习的超参数调整策略并与之结合，形成可根据粒子群离散情况动态调整惯性因子和学习因子的RLPSO。

3.1 DDPG简介

强化学习是机器学习的一个分支，旨在引导智能体在特定环境中依照优化策略采取行动，以最大化累积奖励函数。智能体在离散时间中与环境进行交互，在每一步k中，智能体观察到状态量sk∈S，根据策略π执行动作ak∈A，其中S是状态空间，A是动作空间，策略π：S→A是由S到A的映射。

本文所采用的DDPG 是强化学习的一种分支，是Q 学习在深度神经网络方向的延伸。在DDPG算法中，为获得最优策略π，需设计并调用4 个神经网络，分别为：策略网络μ(sk|θμ)，目标策略网络μ′(sk|θμ′)，动作-价值网络Q(sk，ak|θQ)，目标动作-价值网络Q′(sk，ak|θQ′)。其中策略网络μ和目标策略网络μ′可以根据状态量选择动作，动作-价值网络Q和目标动作-价值网络Q′用于评估所选择动作的优劣，θμ，θμ′，θQ及θQ′代表上述神经网络权重。起始状态下，随机初始化θμ和θQ，θμ′的初始值与θμ相同，θQ′的初始值与θQ相同。训练开始后，目标网络权重按下式更新：

式中：τ≪1，使得目标网络的更新缓慢而平稳，提高了学习的稳定性。

为训练动作-价值网络，需最小化损失函数：

而后利用动作-价值网络训练具有策略梯度的策略网络：

DDPG的训练过程中数据流向如图3所示。

图3 DDPG神经网络训练流程Fig.3 DDPG neural network training process

3.2 状态、动作与网络结构

状态量、动作量和网络结构的详细设计过程可详见于文献［18］，文中仅作简单介绍。状态量能将粒子群当前状态反馈给DDPG 神经网络，动作量则由神经网络根据当前状态给出，经过转换实现算法超参数的动态变化。状态量和动作量的选取与转换决定了DDPG 神经网络的结构，且影响着神经网络与ICLPSO的有机结合。

1）状态量

本文所选择的状态量主要分为3 个部分：迭代进度I、粒子离散度Ddiv、停滞时长Istay。

迭代进度I计算公式如下：

式中：g为当前迭代次数，gemax为迭代次数上限。

粒子离散度Ddiv为各粒子到全局最优粒子欧氏距离的平均值与求解空间内最远距离的比值，计算公式如下：

式中：ρ代表两点间的欧氏距离。粒子离散度越小，表示粒子越集中，反之则表示粒子越发散。

停滞时长Istay表征了当前粒子群算法是否在高效运转，计算公式如下：

式中：glast为上一次全局最优更新时的迭代次数。停滞时长越小，表示当前粒子群运转效率越高。

上述3种状态量取值范围均为［0，1］，为使信息更加突出，避免状态量的小范围变化被忽略，选择正弦编码格式对上述状态量进一步编码，具体方式如下：

式中：x表示3 个状态量中的任意一个；sst_i表示由状态量产生的新分量；i的取值集合为{0，1，2，3，4}。通过上述变换，3 个状态量被转换成为一个15 维的状态矢量，输入到DDPG神经网络中。

2）动作量

本文采用前文2.4 小节介绍的ICLPSO 作为基础，将粒子群分成5 个子种群，每个子种群使用独立的惯性因子w、学习因子c1，c2和c3，每个子种群有4 个待定参数，共有20 个待定参数。以其中一个子种群为例，其4 个待定参数由5 个动作分量{ac1，ac2，ac3，ac4，ac5}产生：

式中：kw=0.8，ks=8，ε=0.000 01，w0=0.1，均为常系数；sscal是用于量化学习因子的中间变量。可见，5 个子种群需要一个25 维的动作矢量作为策略网络的输出。

3）网络结构

在DDPG 智能体中，策略网络μ(sk|θμ)与目标策略网络μ′(sk|θμ′)的网络结构相同，动作-价值网络Q(sk，ak|θQ)与目标动作-价值网络Q′(sk，ak|θQ′)结构相同。设计策略网络结构为15 维输入25 维输出的神经网络，结构如图4（a）；设计策略网络结构为40维输入1维输出的神经网络，结构如图4（b）。

图4 DDPG神经网络结构Fig.4 DDPG neural network architecture

3.3 奖励函数设计

结合实际问题背景，取种群数量N=100，种群维度D=2，分成5 个子种群，每个子种群有20 个粒子，迭代次数上限gemax=128，收敛迭代次数上限gcmax=50，个体最优位置持续4 代未更新时重新选择较优粒子群。

奖励函数的设计关乎到神经网络训练的成败，不合适的奖励函数会使得神经网络出现懒惰倾向和刷分倾向。懒惰倾向指因为错误动作惩罚过大，神经网络的行为偏向保守，虽然能够快速收敛，但所得解并非全局最优解；刷分倾向指因为单步奖励值设置过大，神经网络倾向于小步前进，从而获得更多奖励，虽然最终能收敛到全局最优解，但收敛代数多，收敛速度慢。

在以往利用强化学习优化智能算法超参数的研究中，往往采用如下简单奖励函数：

式中：J*(k)为第k次迭代后算法所求的全局历史最优适应度，该值在每次迭代后只会变得更优（即更小）或保持原值不变，因此仅有J*(k) ＜J*(k-1)和J*(k)=J*(k-1) 两种情况，而不会出现J*(k) ＞J*(k-1)。该奖励函数旨在通过奖励有效迭代、惩罚无效迭代使得粒子群快速收敛，但因奖励函数设计单一，神经网络经常出现懒惰倾向和刷分倾向。为改善以上情况，引入PSO 优化解作为参考基准，设计日常奖励函数如下：

式中：σ=0.001，为误差系数，即认为所提算法优化解劣于PSO 优化解1‰以内仍是成功的结果，给予正向的最终步奖励，该常系数的设置是为了改善训练过程中曲线的频繁震荡情况。

上述日常奖励函数通过合理的数值设计和引入参考基线，防止了懒惰倾向的产生，同时通过设计数值合适的最终步奖励函数，鼓励算法快速收敛到最优解，防止了刷分倾向的产生。

3.4 RLPSO算法设计

将训练好的DDPG 神经网络与ICLPSO 结合，形成RLPSO算法如下：

算法2.强化学习粒子群算法

1）初始化粒子群；

2）使用式（8）计算粒子适应度，并分别记录全局最优和个体最优；

3）如当前粒子个体最优值停滞超过m代未更新，则通过锦标赛规则更新优胜粒子群；

4）使用式（16）～（18）计算状态量，使用式（19）编码为状态矢量输入到DDPG神经网络中；

5）使用式（20）将DDPG 神经网络输出的动作矢量转换为各子种群的惯性因子w、学习因子c1，c2和c3；

6）使用式（12）更新粒子群；

7）更新收敛迭代次数和迭代次数，如触碰收敛迭代次数上限gcmax或迭代次数上限gemax则算法结束输出最优解，否则返回2）继续迭代。

RLPSO 算法与前述各算法的继承关系如图5所示。

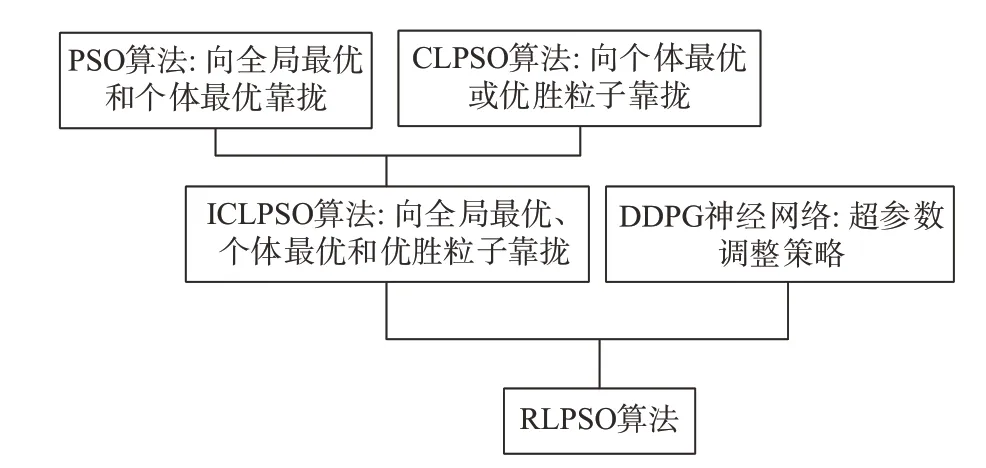
图5 RLPSO算法继承关系Fig.5 Inheritance relationship of RLPSO

4 仿真实验

本节首先给出用于DDPG 网络训练的详细参数，并在后续的仿真实验中，采用交会任务时长上限不同的两组实际服务航天器和目标航天器数据，分别用RLPSO、PSO 和CLPSO 求出迭代次数ge、燃料最优值Jbest、时间最优解Gbest以及脉冲Δv1和Δv2，并进行比对分析。

4.1 DDPG网络训练

考虑到同步轨道单次转移实际可接受的速度增量一般在100 m/s 量级，且需满足前文1.1 小节基本假设，取如下限制的一族典型工况作为神经网络训练的待解问题：两航天器轨道半长轴在41 966～42 366 km 之间随机选取，偏心率在0～0.005 之间随机选取，轨道倾角在0°～0.05°之间随机选取，升交点赤经选为0°，近地点幅角选为0°，目标航天器真近点角选为0°，服务航天器真近点角在-25°～25°之间随机选取；交会任务时间上限取86 400 s（同步轨道周期）。为使得DDPG 智能体更好地进行探索学习，在训练过程中向动作矢量加入不相关的、均值为0、方差为0.5的高斯噪声，如下式所示：

设置折现系数γ=0.99，策略网络学习率取2 ×10-4，动作-价值网络学习率取1 × 10-3，相比于策略网络更高的学习率有助于动作-价值网络更快做出准确评估，经验回放缓存长度设置为3 × 104。按上述条件进行50 000 轮次仿真训练，选取表现最好的DDPG神经网络。

取迭代进度I为0.5，停滞时长Istay为0.05，粒子离散度Ddiv取值区间为［0.1，0.9］，将以上3 量编码为状态量输入训练好的DDPG 网络中，将所得动作量转换为5 组待定超参数，其中一组超参数随粒子离散度变化曲线如图6 所示，可以看出训练好的DDPG 网络实现了根据粒子群收敛情况实时调整超参数的预定目标。

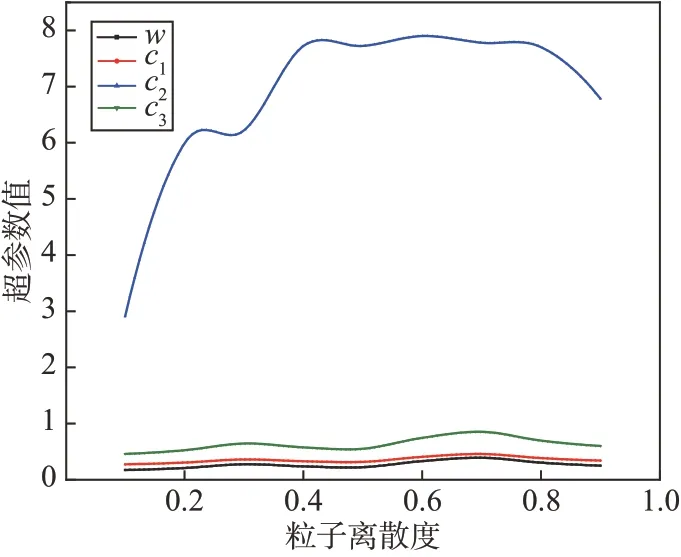
图6 超参数随粒子离散度变化曲线Fig.6 Curves of hyperparameters changing with particle diversity

4.2 单次实验结果对比

单次仿真实验结果对比所用两航天器轨道根数见表1。在本小节实验中，PSO、CLPSO 和RLPSO算法参数如表2所示，交会任务时长上限较短，需在1天（86 400 s）内完成。

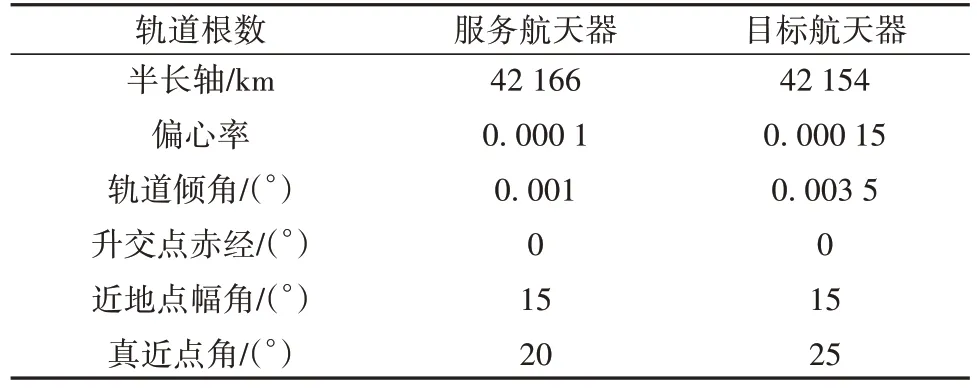
表1 单次仿真实验所用航天器轨道根数Table 1 Orbital elements of spacecrafts used in a single simulation experiment

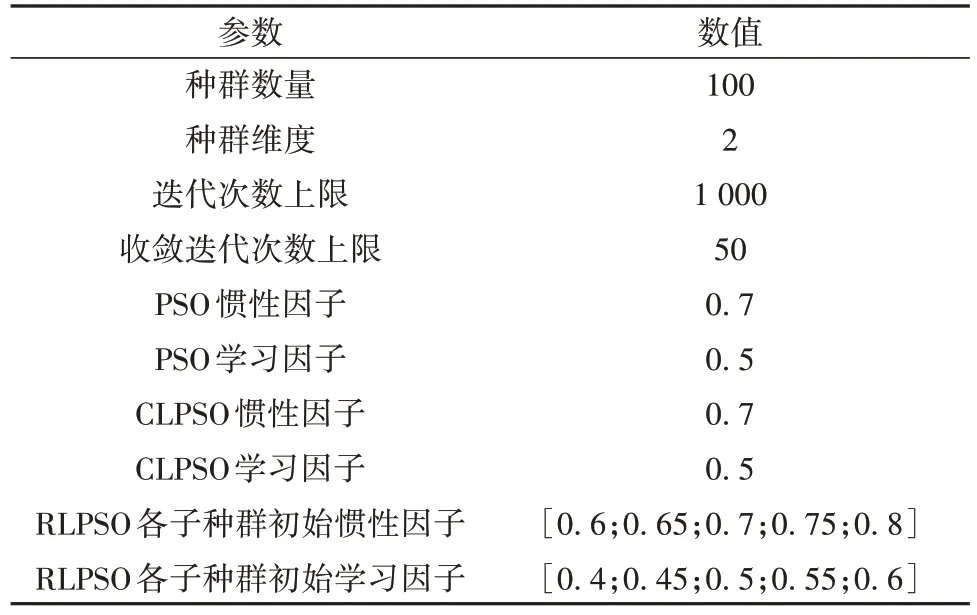
表2 算法参数Table 2 Algorithm parameters

为了验证所提算法的实用性，针对上述工况，在粒子群规模相同的情况下，分别利用RLPSO、PSO和CLPSO 进行单次燃料最优转移策略求解。单次仿真实验结果对比如表3所示。在变轨策略的优化求解中，单次轨道外推计算量很大，与之相比粒子群位置、速度的计算及通过神经网络计算超参数的时间几乎可以忽略不计，迭代次数的缩减能够在相当程度上节约计算时间。相比于PSO，RLPSO 在迭代次数上缩减了49.54%并取得了更好的优化解；相比于CLPSO，RLPSO 在迭代次数上缩减了55.64%，而优化误差仅扩大了0.016%，可满足实际工程需要。

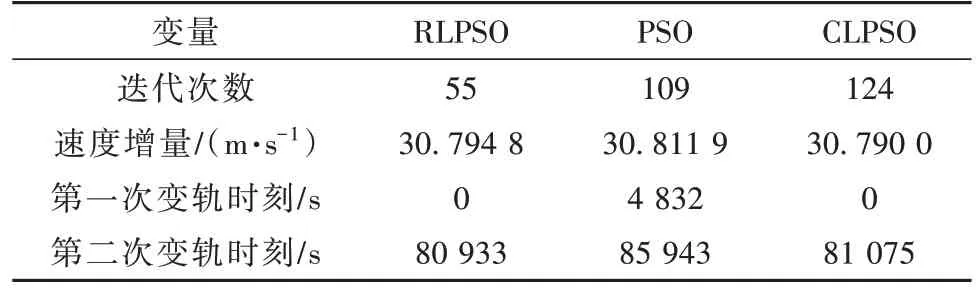
表3 单次仿真实验结果对比Table 3 Comparison of single simulation experimental results

3种算法的最优解收敛过程如图7所示，可以看出，在首代全局最优值相近的情况下，RLPSO 仅经过5 次迭代就收敛到其最终优化值，此时PSO 和CLPSO 优化值为30.813 1 m·s-1和34.063 4 m·s-1，均劣于RLPSO的优化值30.794 8 m·s-1。

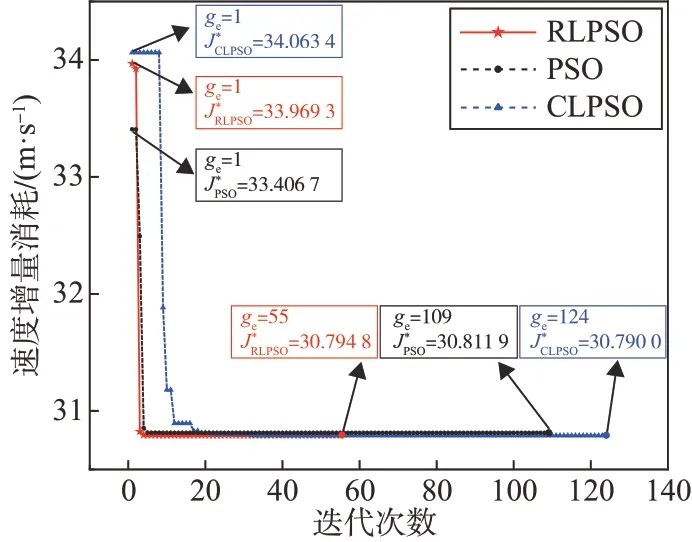
图7 RLPSO、PSO和CLPSO收敛过程对比Fig.7 Comparison of convergence processes of RLPSO，PSO and CLPSO

将二体模型下所求得的脉冲矢量代入到考虑J2摄动的轨道动力学模型中，通过轨道外推得到两航天器在第二次脉冲机动后，位置仅相差0.103 6 km，可继以末端制导完成交会，验证了算法的可行性。

4.3 多次实验结果对比

多次仿真实验结果对比所用两航天器轨道根数见表4。在这次仿真实验中，PSO，CLPSO 和RLPSO 算法参数仍为表2 中参数，为进一步验证算法的有效性，增大两航天器轨道高度差和相角差，同时加长交会任务时长上限，需在5 天（432 000 s）内完成，更长的时长上限意味着更大的解搜索空间，对算法的搜索性能要求更高，同时相比于4.2小节中与训练工况相同的时长上限，本小节实验亦对算法的泛用能力做出了检验。

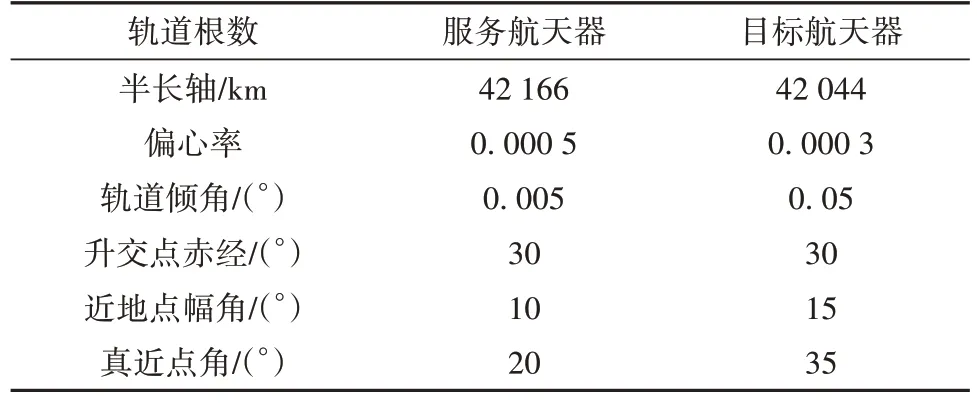
表4 多次仿真实验所用航天器轨道根数Table 4 Orbital elements of spacecrafts used in multiple simulation experiments

针对上述工况，分别使用PSO、CLPSO和RLPSO进行20 次燃料最优转移策略求解。多次实验结果对比如表5 所示，仿真过程使用个人计算机完成，CPU 型号为Intel Core i7-11800H @ 2.30 GHz，内存为16 GB。

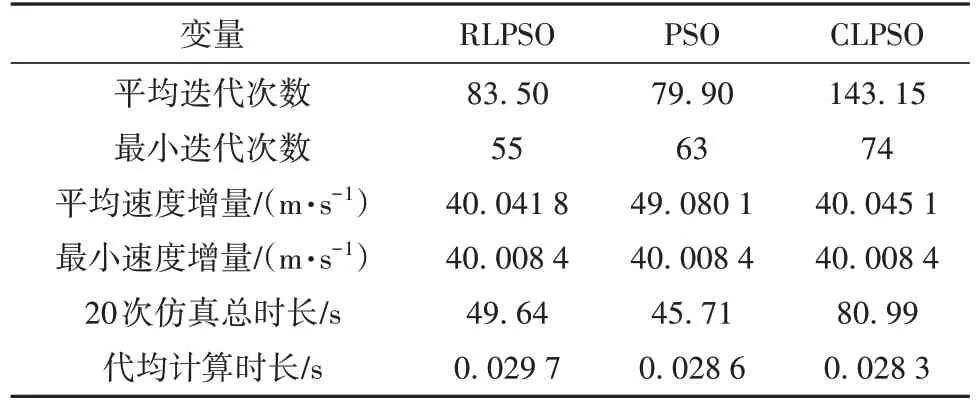
表5 多次仿真实验结果对比Table 5 Comparison of multiple simulation experimental results

虽然RLPSO 的迭代代数与总计算时长略逊于PSO，但RLPSO在优化精度上占据显著优势；相比于CLPSO，RLPSO 在迭代代数与总计算时长上占据显著优势，且在优化精度上也优于CLPSO。上述结果反映出RLPSO 的参数自适应机制能够更好地适应较长时间规划任务，更大的初始轨道差异也进一步证明了方法的有效性。这说明RLPSO 算法在更大的解搜索空间的问题上体现出了良好的泛用能力，也说明采用短时间规划任务进行训练并在较长时间规划任务中应用是可行的，这一结果利于神经网络的快速训练与部署。需要注意的是，相比于PSO和CLPSO，在粒子群规模相同的情况下，RLPSO 的代均计算时长明显更长，这是由于深度神经网络对超参数的自适应计算消耗了部分计算资源，但即便如此，由于迭代次数的压缩，RLPSO 的计算速度仍然具有相当的竞争力。

5 结论

本文针对考虑燃料最优的GEO 航天器交会Lambert变轨策略优化问题建立了数学模型，引入了ICLPSO 作为变轨策略优化的基础方法，并探索运用DDPG 神经网络实现算法超参数的动态自适应调节，将DDPG 与ICLPSO 组合为RLPSO，在牺牲较小求解精度的前提下大幅压缩了算法迭代次数，改善了以往航天器交会变轨策略优化方法计算资源消耗大的问题，最后通过仿真实验验证了所提算法的有效性和可行性。研究成果及总结展望如下：

1）建立了GEO 航天器交会Lambert 变轨数学模型，给出了速度增量消耗与变轨时刻的关系，可用于粒子群算法的代价函数计算与DDPG 神经网络的奖励函数计算。

2）引入了在PSO 的基础上结合CLPSO 中的优胜粒子跟随机制ICLPSO，并使用一族典型GEO 航天器交会工况训练DDPG 神经网络，将DDPG 与ICLPSO 结合形成算法超参数可动态自适应调节的RLPSO。将PSO优化解作为参考基线引入训练环境奖励函数的设计中，避免智能体出现懒惰或刷分倾向，仅通过50 000 轮次训练就取得了较好的应用效果。仿真结果表明，与PSO 和CLPSO 相比，RLPSO在牺牲了不到1‰的优化精度的前提下大幅压缩了迭代次数，节约了计算资源，优化结果能够满足实际工程需求，同时在大搜索空间下，RLPSO 仍然保持住了优化精度，相比PSO 和CLPSO 的优势变得更加明显，迭代次数的缩减带来的低计算量或使得该算法应用于星上自主交会规划成为可能。

3）本文算法除GEO 航天器交会Lambert 变轨策略优化问题外，在进行适应性修改后还可能应用于如多脉冲变轨策略优化等其他航天器决策优化问题，并亦可应用于除二体模型以外的轨道动力学模型，相比于二体模型，其他较高精度轨道动力学模型因迭代次数压缩带来的计算资源节约将更为明显。未来可以聚焦于上述两点对算法进行进一步的扩展应用。