空间包络式抓捕机构非接触/接触一体化导纳控制

刘 磊，张 涛

（1.空间智能控制技术全国重点实验室，北京 100094；2.清华大学自动化系，北京 100084）

0 引言

随着人类航天活动更加频繁，失效卫星、火箭上面级等空间碎片占据着重要的轨道资源，并对在轨运行航天器的安全性造成重大威胁［1-4］。这类目标通常不具备专门的抓捕对接装置，几何形状和运动状态均未知，属于典型的非合作目标。非合作目标的接触式刚性捕获方法包括单臂抓捕、多臂抓捕以及并联机构抓捕等。单臂抓捕通常依赖末端夹爪，仅适用于抓捕存在夹持点的空间碎片。多臂抓捕机构灵活性好，能够实现多样性的抓捕策略，如指尖抓捕、多指节抓捕等。指尖抓捕仅通过多臂的末端（指尖）与目标形成接触点，需要较为精细的控制［5］。多指节抓捕涉及不同臂杆（指节）与目标表面的接触，能更好地适应目标形状［6-7］。随着近年来地面类人手的发展，一些欠驱动类人手的设计方案也被应用到空间碎片抓捕领域，其模仿人手的结构与运动，能够自然地抓取大型目标［8］。多指节抓捕与类人手抓捕在一定程度上都可视作包络式抓捕方法，通过将目标完全包围从而提高抓取稳定性。然而，通过优化方法快速精确求解接触点与接触力仍然是极具挑战性的任务。

除了多臂形成的包络抓捕，有学者提出了一种空间包络式的并联抓捕机构，该机构通过多个臂杆铰接形成包络体，依靠机构与目标的多点多次接触，完成对目标的牢固捕获［9］。与目前常见的飞网柔性抓捕、多臂抓捕等方式相比，该方案具有适用性强（对目标的大小、形状要求不高，且无需专门的对接装置）、捕获难度低（无需测量或估计目标的运动状态）、捕获牢固（通过多点加持，实现牢固捕获）的特点［9］。但是，该机构的构型复杂，受到多个闭环约束，导致动力学和运动学建模难度大，进一步给控制设计带来困难。相应的建模方法包括变拓扑动力学［10］、旋量理论等。本文以空间包络式抓捕机构为研究对象，建立其动力学模型，针对捕获过程的控制，提出一种非接触/接触一体化的导纳控制方案，实现捕获过程的柔顺控制。

目前，在机器人的主动柔顺控制领域，力/位置混合控制［11］与阻抗控制［12］是应用较为广泛的两种控制策略。其中，广义的阻抗控制包括基于力的阻抗控制（阻抗控制）以及基于位置的阻抗控制（导纳控制）。在导纳控制中，控制器输入力信号并输出位置修正信号［13］。有许多研究成果验证了将柔顺控制应用于空间机器人的可行性［14-16］。Palma 等［17］利用仿真验证了柔顺控制在处理机器人接触问题中的优势。Uyama等［18］提出一种基于阻抗控制的自由飞行空间机器人的接触控制策略，并执行了利用柔性机械臂捕获非合作目标的数值仿真。Hirano等［19］提出了一种鲁棒控制方案，验证了控制策略在捕获大型旋转目标在线路径规划和柔顺控制的可行性。Liu 等［20］关注柔性关节空间机器人的柔顺控制问题，提出了一种非奇异复合阻抗控制器。聂佳伟等［21］分别采用位置控制与位置型阻抗控制，证明了阻抗控制能够更加柔顺地控制机械臂与接触面进行接触。此外，还有学者关注了捕获后操作目标的柔顺控制。王明明等［22］针对抓捕非合作目标卫星的运动稳定问题，提出了一种空间机器人最优消旋策略和协调控制方法。刘磊等［23］针对空间大质量目标双臂转位操作，提出了一种协调控制方法。韩冬等［24］针对空间机器人抓捕目标后构成的组合航天器的稳定控制问题，提出了基于反作用轮重配的反步积分滑模控制方法。樊茂等［25］针对空间机器人抓捕目标中产生的碰撞冲击问题，提出了一种低能耗、小扰动的镇定控制方法。

除接触碰撞阶段外，在空间机器人接近目标阶段，同样可以采用合适的控制策略降低机器人与目标的碰撞冲击，以实现机器人的柔顺性。例如，Suarez等［26］在一种柔性轻型双机械臂系统中验证了在没有关节电机的情况下的可变阻抗技术，实现机械臂与外部环境的柔顺接触；Ramón 等［27］利用视觉伺服控制算法，实现视觉特征信息辅助机械臂的阻抗控制；Xu等［28］提出了一种基于图像的双自由度机械臂阻抗控制策略，并将控制过程分为运动控制与自适应视觉阻抗控制两个阶段。除了借助视觉特征的辅助的方法，Arai 等［29］最早提出虚拟阻抗的概念，通过在机器人与未接触的目标之间产生虚拟阻抗力来实现机器人对环境的阻抗特性。但其聚焦于避障路径规划问题，本质是将系统视为机械阻抗，无法直接与接触导纳控制相统一。Tsuji 等［30］则在虚拟阻抗的基础上利用视觉反馈信息设计了机器人与目标之间的非接触式阻抗控制方法，实现避障或减小首次碰撞力。目前，非接触与接触导纳控制一体化控制方法还没有被提出，这种一体化控制方法能够灵活应对不同的接触工况与任务场景，而无需修改底层控制器结构与参数。

综上，针对机械臂与目标接触前后的柔顺控制问题，提出一种非接触与接触导纳控制的统一方法，在机械臂接近目标时采用非接触式导纳控制，降低接触时刻机械臂受到的接触力；在抓紧目标过程中采用接触式导纳控制，实现目标的柔顺接触，避免捕获失败。两种阶段的导纳控制输出量具有相同的形式，避免了控制器切换的困难。

1 系统描述与动力学建模

1.1 空间包络式抓捕机构系统描述

如图1（a）所示，空间包络式抓捕机构的主体由3RRS 并联机构（Revolute-Revolute-Spherical 的铰链配置，各臂杆编号分别为11、12、21、22、31、32）以及Bricard 机构（各臂杆编号12A、12B、22A、22B、32A、32B）两部分组成［5］，并安装于上平台，再与卫星本体连接。系统共包括14个刚体。3RRS和Bricard机构的运动学分析见文献［31］。由于机构内部有复杂的闭环约束，为建立最小维数的系统动力学模型，选取Bricard机构内C1、C2、C3处的柱铰作为切开点解除闭环约束，所得等效开环系统结构如图1（b）所示。

图1 空间包络式抓捕机构与等效开环系统的结构示意图Fig.1 Structural diagram of the spatial envelope capture mechanism and its equivalent open-loop system ［31］

图1 中空间包络式抓捕机构的自由度分析如下：星体b于惯性空间中自由漂浮，具有平动和转动的6个自由度；上平台与星体之间通过柱铰连接，具有1个相对自由度；3RRS并联机构中臂杆11、21、31分别与上平台之间、臂杆12、22、32 分别与臂杆11、21、31之间都通过柱铰连接，一共具有6个相对自由度；Bricard 机构与3RRS 并联机构的三个臂杆连接顺序为i2-i2A-i2B，其中i2-i2A 为球铰连接，各具有3 个相对自由度，i2A-i2B 为柱铰连接，各具有1 个相对自由度。整个系统的独立自由度数量为11个。

1.2 考虑包络闭环约束的动力学模型

为了完成系统的动力学建模，首先在Bricard 中间的三个铰链C1，C2，C3处引入切开点，得到等效开环系统，该系统具有25个自由度，选取广义速率为

针对等效的开环系统，可建立如下形式的动力学方程

在切开点处的约束方向上，两端的速度、角速度相等，基于该物理事实可得系统受到的约束形式为

式中：A为约束矩阵，是系统的几何参数、构型坐标的函数。对式（4）求导即为系统的加速度约束方程

结合式（3）和式（5）可写出空间包络式抓捕机构的动力学方程为

式中：μ为拉格朗日乘子，其物理意义为切开点两端所增加的未知约束力。一般情况下可由方程求解μ，其通解表示为

式中：z为元素可取任意值的15维向量。将式（7）代入式（6）可得系统动力学响应为

1.3 抓捕过程中的接触模型

针对空间包络抓捕机构的运动仿真，需要描述机构与目标之间的接触碰撞过程。首先利用计算机图形学方法进行碰撞检测。假设各臂杆和空间目标外形均为圆柱体，各关节形状为球体，则碰撞检测问题简化为两圆柱体之间、圆柱体和球体之间的碰撞。当检测到碰撞时，通过接触碰撞模型计算当前时刻接触碰撞力大小，使用Flores 模型作为机械臂末端与星体表面之间的法向接触碰撞模型，此模型中接触力的表达式为

滞后阻尼因子为

式中：K为接触刚度系数；δ表示两接触刚体法向嵌入深度；n为力系数；Cr为恢复系数；表示本次碰撞开始时刻的二者接触点表面切向相对速度。

选取静摩擦、库伦摩擦以及Stribeck 现象三者组合的模型用来描述接触过程中切向摩擦力的情况，该组合模型表达式可写为

表1 捕获目标过程接触碰撞的相关参数Table 1 Contact collision related parameters during the process of capturing targets

2 非接触/接触一体化导纳控制

本文所提出的非接触/接触一体化导纳控制框图如图2 所示。根据广义碰撞力观测器（2.2 节）的观测结果，当空间包络抓捕机构与非合作目标没有发生接触时，采用非接触式虚拟导纳控制（2.1 节），根据虚拟阻抗模型和独立关节空间虚拟导纳模型，得到关节运动的修正量，避免与目标发生较大的初次碰撞力；当空间包络抓捕机构与非合作目标发生接触后，控制器更改为接触式导纳控制（2.3 节），同样输出关节运动的修正量，实现期望的夹持状态。由于两种控制输出相同，底层控制回路则采用轨迹跟踪控制器，在切换前后无需调整控制参数。

图2 非接触式和接触式一体化导纳控制框图Fig.2 Block diagram of non-contact and contact admittance control

2.1 非接触式虚拟导纳控制

空间包络式抓捕机构在接近目标过程中，需要添加主动的减速过程，以降低首次与目标接触时的碰撞力，避免机构的损坏。本节通过设计非接触虚拟导纳，实现接近目标过程的柔顺控制。首先在可能发生碰撞的关节处设计虚拟球，利用虚拟阻抗模型计算得到虚拟阻抗力，并将其转换为广义虚拟阻抗力；其次，设计虚拟导纳模型将此广义虚拟阻抗力转换为轨迹修正量对期望轨迹进行调节，使得各关节跟踪修正后的轨迹。

考虑如图3所示的机械臂第i个关节，定义半径为r(i)(i=1，2，…，N)的虚拟球，每个虚拟球的球心均位于关节中心。虚拟阻抗控制器的输入为机械臂臂杆与目标之间的位置、速度和加速度信息，输出为虚拟阻抗力。

图3 非接触式阻抗控制原理图Fig.3 Schematic diagram of non-contact impedance control

在以下推导中，若未做特殊说明，各位置、方向物理量均表示在机构安装的上平台坐标系中，见图1（a）中的x1y1z1坐标系。假设将要接触的物体位置坐标为Xo，当物体进入虚拟球i的内部时，定义从虚拟球表面到物体的法向为

式（14）即为非接触阻抗模型，又称虚拟阻抗模型。由式（13）与式（14）可以看出，当物体处于虚拟球球心处或未进入虚拟球时，虚拟阻抗力均为零；而当物体处于虚拟球内部且未与球心处关节接触时，此虚拟阻抗力可根据虚拟球心所在关节处的雅克比矩阵转换为各个关节的作用力矩。考虑到加速度反馈所带来的噪声影响，可忽略加速度项。独立关节空间下的广义虚拟阻抗力可写为

则修正的期望轨迹为

2.2 考虑闭环约束的动量观测器

空间包络式抓捕机构在与目标发生接触后，需要进行碰撞检测，根据接触程度改变各个自由度的运动。一种解决方法是在各臂杆配置类人皮肤传感器，然而这将大大增加机器人硬件系统的复杂度、降低可靠性。另一种思路则是利用安装在机器人本体的运动传感器和力学传感器测量信息对机器人与外界间的接触碰撞情况进行观测，实时获得碰撞力对各关节的广义外力，即广义碰撞力。目前大部分对广义碰撞力的观测仅限于树形系统，本节针对空间包络式抓捕机构，引入考虑闭环约束的动量观测器，实现接触识别以及接触力的估计。

本文所研究的空间包络式抓捕机构存在多闭环结构与冗余约束，其内部真实约束力难以得到，而且实时求解多处接触碰撞点的位置和碰撞力信息较为困难，因此选择直接利用观测器所观测到的广义碰撞力信息设计各关节的接触式阻抗控制。与传统的开环或链式机械臂的动力观测器不同，为了消除闭环约束造成的观测难度，引入最小数目的传感器测量闭环约束中的约束力，即式（7）中的μ。

由空间包络式抓捕机构动力学方程（6）可知，在有碰撞情况下的动力学方程为

式中：β=Cu-。观测器形式为

式中：KMO为观测器增益上标“^”表示测量或计算得到的值。

由式（20）和式（21）可得

由式（22）可以得出观测器的输出γ能够实现对FGC的指数跟踪，因此空间包络式抓捕机构广义碰撞力的观测可由观测器（21）来实现，观测器具体的结构如图4所示。

图4 空间包络式抓捕机构广义碰撞力观测器Fig.4 Generalized collision force observer for spatial enveloping capture mechanism

2.3 接触式导纳控制

依靠碰撞观测器，可以设计接触式导纳控制器，该控制器的输入是碰撞力，输出是轨迹修正量。

独立关节空间下的广义碰撞力可写为

独立关节空间下的阻抗模型为

则修正后的独立关节期望轨迹为

观察式（17）和（26），非接触式虚拟导纳控制和接触式导纳控制有一致的输出形式，可自然地将两种控制融合在一起，形成非接触/接触一体化导纳控制。

3 数值仿真

对空间包络式抓捕机构抓捕目标的柔顺控制过程进行仿真分析。空间包络式抓捕机构的质量和尺寸参数如表2所示。

表2 空间包络式抓捕机构质量与尺寸参数Table 2 Mass and size parameters of spatial enveloping capture mechanism

本节仿真中空间目标的质量和尺寸参数在表3中定义，阻抗模型参数以及轨迹跟踪控制器参数列于表4。其中，阻抗模型参数的数量级与原系统保持一致，在选取刚度矩阵后按二阶系统特性近似选取质量矩阵与阻尼矩阵；独立关节空间修正量只作用于3RRS 以及Bricard 机构的4 个独立自由度；此外，3RRS的三个独立关节阻抗参数应保持相同。空间包络式抓捕机构将以六点式夹持方式完成对目标的柔顺捕获。抓捕任务的初始时刻与结束时刻系统构型如图5所示。初始时刻星体速度、角速度及各关节角速度均为零；目标轴线垂直于抓捕网口、中心位于[0 0 -15]Tm，初始速度为[0 0 -0.05]Tm/s、角速度为零。期望抓捕状态下，空间包络式抓捕机构各关节角速度、角加速度均为零，期望的部分关节运动轨迹如图6所示。

表3 空间目标质量与尺寸参数Table 3 Space target mass and size parameters

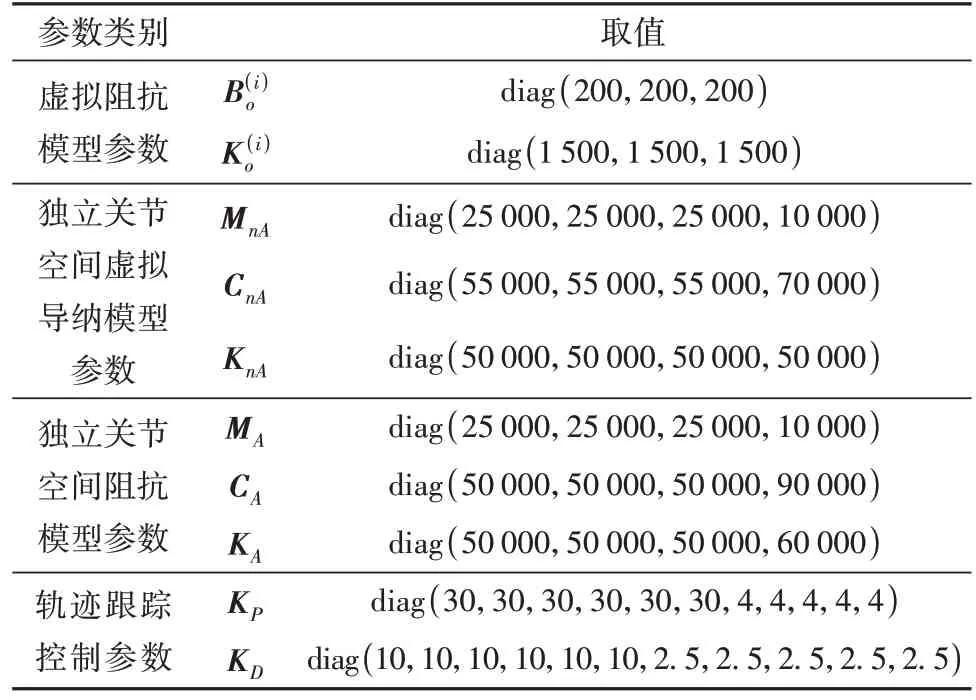
表4 控制器参数Table 4 Controller parameters

图5 抓捕任务初始时刻与结束时刻系统状态Fig.5 System state at the initial and terminal moment of the capture task

图6 空间包络式抓捕机构关节期望轨迹Fig.6 Expected trajectory of joint in spatial enveloping capture mechanism

对比使用传统的位置控制和本文提出的非接触/接触一体化导纳控制（后简称“柔顺控制”）的效果。以臂杆12A 为例，分别给出位置控制与柔顺控制作用下，空间包络式抓捕机构与目标的接触情况，如图7所示。

图7 空间包络式抓捕机构与目标接触情况（0：无接触，1：动摩擦，2：静摩擦）Fig.7 Contact between spatial enveloping capture mechanism and target（0：non-contact，1：dynamic friction，2：static friction）

可以看出，在位置控制下，Bricard 机构各个臂杆与目标之间发生碰撞后被碰撞力弹开，接触面发生分离，之后二者经过若干次碰撞过程才最终保持接触，但最终的稳定状态二者之间仍存在滑动摩擦，说明位置控制下空间包络式抓捕机构对存在0.05 m/s 相对运动的10 m 尺寸目标并不能有效地进行捕获。在柔顺控制下，当广义碰撞力观测器观测到抓捕机构与目标碎片的首次接触后，控制器将立即调整为阻抗控制模式，对各关节实时施加阻抗作用、调整抓捕机构对外展现的阻抗特性，从而避免了抓捕机构与目标碎片接触后的分离，以较快的速度实现了可靠的抓捕。

图8分别给出了与空间包络式抓捕机构关节运动对应的广义碰撞力。位置控制下抓捕机构将与目标碎片发生多次、多点的接触碰撞，在接触稳定前抓捕机构臂杆及各关节将受到多次冲击；而柔顺控制下机构在接触目标碎片后不再与其分离。同时可以看出，在非接触导纳的作用下，首次碰撞的接触力明显减小，避免了对结构带来较大的冲击。此外，柔顺控制下抓捕机构与目标碎片间最终的接触力大于位置控制。原因在于，柔顺控制中通过阻抗作用对抓捕关节的刚度进行了调整，从而产生了“抓紧”目标碎片的效果；而传统的位置控制不具备此能力。

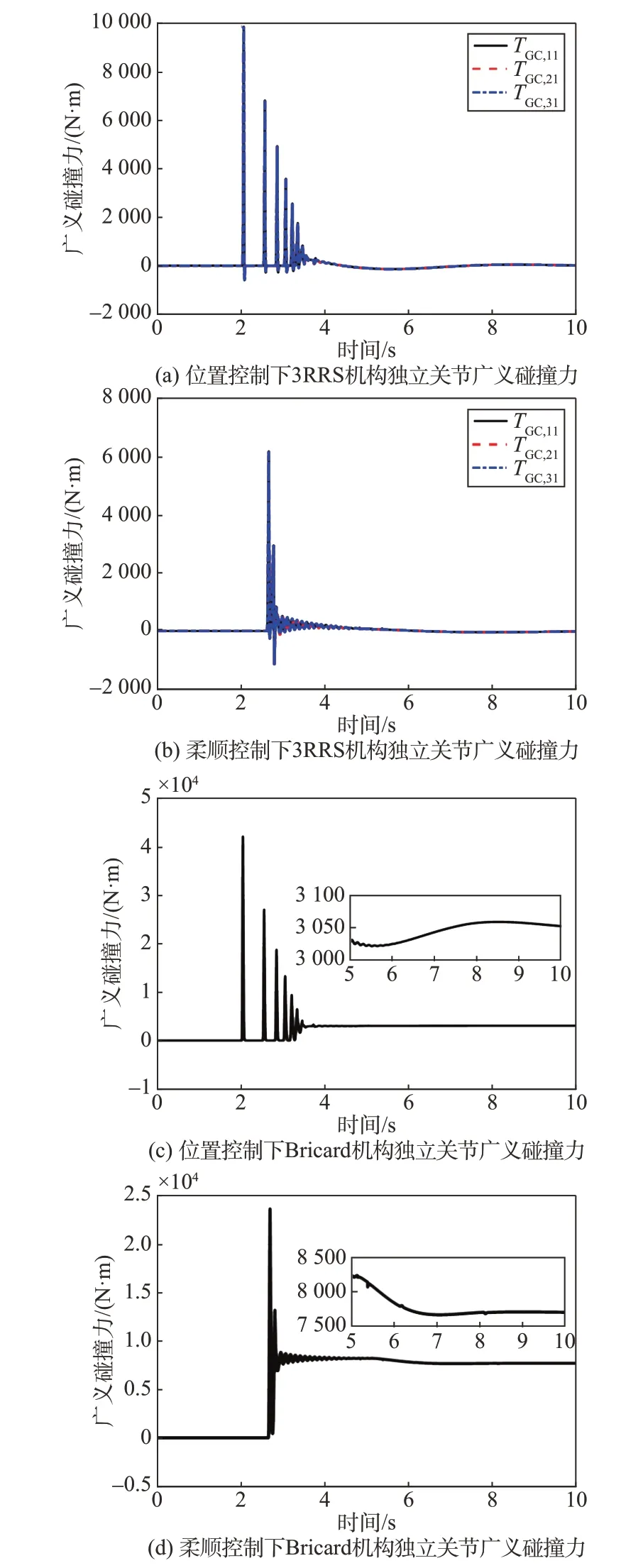
图8 3RRS结构与Bricard机构对应的广义碰撞力Fig.8 The generalized collision force corresponding to the 3RRS structure and the Bricard mechanism

图9 以Bricard 机构中关节12B 为例，给出其期望轨迹、修正的期望轨迹以及两类控制下实际转角的图线。该转角的变化情况表征了空间包络式抓捕机构的抓捕网口大小的变化情况。可以看出，柔顺控制根据观测的广义碰撞力及阻抗模型对关节期望轨迹进行了修正，使其较快地收敛于接触稳定位置。同时，由于位置控制和柔顺控制分别对原期望轨迹和修正后的期望轨迹进行跟踪，因此两类控制下关节12B 的实际转角变化情况也有较大差别：位置控制下由于抓捕机构与目标的多次接触碰撞，关节转角12B 在首次接触后将发生多次弹跳，而柔顺控制下该转角将较快地稳定于稳态值。

图9 位置控制与柔顺控制模式下关节12B转角Fig.9 Angle of joint 12B in the traditional position control and the proposed control

4 结论

本文以带有复杂闭环约束的空间包络式抓捕机构为研究对象，提出了一种非接触式与接触式一体化的导纳控制方法，实现对非合作目标的柔顺捕获。首先建立了系统显式的动力学模型，其次设计了空间包络式抓捕机构与目标的碰撞检测和非接触式与接触式一体化的导纳控制。一方面，在接近目标过程中，采用非接触的导纳控制策略，降低抓捕机构与目标首次发生碰撞的接触力；另一方面，在首次接触后转换为接触的导纳控制策略，根据接触力的观测结果动态调整关节的期望轨迹，减少抓捕机构与目标的接触次数，且能获得更大的夹持力实现稳定捕获。数值结果表明，所提方法能够有效降低空间包络式抓捕机构与目标物体首次接触的危险，同时更快地实现稳定捕获。