考虑振动损耗的生鲜冷链运输路径规划
钱文杰,陆敬筠
(南京工业大学 经济与管理学院,江苏 南京 211816)
0 引言
现存冷链物流损耗研究多集中于货物易腐性,从温度控制入手进行研究。Osvald[1]提出将新鲜蔬菜的易腐性作为配送优化的考虑因素;随着冷链物流技术的发展,越来越多的影响冷链物流货物品质的因素在实践中被发现,Rodriguez 等[2]指出服务顾客时冷藏车厢的开闭时间长短和频率导致的温度变化会影响生鲜品质,缪小红[3]在研究第三方冷链物流配送路径优化时将Rodriguez 指出的腐坏因素进行拓展,将生鲜腐坏分为运输途中的损耗与服务顾客时车厢门开闭造成的损耗,通过货损比例进行货损量以及成本的计算;吕宁等[4]测定了冷藏车开关门温湿度变化,提供了进一步深化研究服务顾客装卸农产品时车厢内温度对农产品失去温度保障后产生品质变化的研究依据,在这个基础上,沈丽等[5]在货损的计算上考虑了搬运物理碰撞、运输过程中自然变质造成货损与开闭车门装卸使农产品失温货损。
综合上述研究可以看出在计算冷链物流货损时侧重于运输与装卸过程中货品呼吸作用造成的变质腐败,计算物理损耗以碰撞损伤为主。实际运输过程中,振动损伤始终存在。魏巍等[6]总结了果蔬运输振动损伤研究,指出模拟实验为主要研究果蔬运输振动损伤[7]的方法,并总结出模拟运输实验的主要因素:振动加速度和振动时间。根据王妮睿等[8]的实验结论,振动传递率与层数成正比,张鸣宇等[9]在计算同间隔层数的包装振动传递率测试结论证明振动传递率增速随层级变高放缓。根据王璐璐等[10]的振动实验结果,振动传递率与振动时间在总体上振动传递率随时间先增大后减小,并趋于一个稳定值。
本文拟加入货品运输过程中振动损伤计算,对运输损耗模型进行拓展,通过比较综合计算振动损伤和变质损耗的运输路径最小损耗量与仅考虑自然变质损耗最小的运输路径的振动损伤和变质总体损耗量,探究控制运输振动损耗的必要性。
1 问题设定与参变量量描述
1.1 问题假设与描述
对问题进行描述可以表达为:从配送中心派出同一类型车辆对多个服务需求点进行配送服务,运送到各点的货品品种相同。再计算综合损耗最低的情况下的最优路径。
假设每一辆车从配送中心出发,最后返回配送中心,载重不得超过额定载重;服务需求点位置与需求量都是已知的,且一个服务需求点由一辆运输车满足服务,装卸过程中装卸速度为一确定值,运输车辆行驶速度为匀速。
1.2 基本参数与变量说明
n 表示需求服务点数量;
K 表示配送车辆数量;
L 表示配送过程产生的总损耗;
L1表示运输距离造成的损耗;
L2表示装卸失温变质损耗;
β 表示温度敏感因子;
θ 表示装卸腐败系数;
dij表示配送点i 到j 的距离;
xijk表示该项等于1 时运输车k 由i 向j,否则取0;
εij表示运输变质货损系数;
δ 表示货物对时间敏感系数;
qi表示需求服务点i 的需求量;
v 表示运输车辆行驶速度;
s 表示装卸速度。
2 模型构建
2.1 运输产生的振动损耗成本计算
计算冷链运输途中果品的振动损伤。设运输时车辆振动频率为f0,车辆振动加速度为G0,堆放层数为c,第c 层振动加速度Gc,振动传递率[7]Tc,第c 层果实损耗率μc。不同的振动频率对应不同的振动加速度。综上可得:
计算振动传递率时使用稳定后的振动加速度值与实验振动台加速度值比较确定振动传递率[8],本文设振动传递率最大影响因素为货品堆放层数与包装缓冲结构,可以将振动传递率描述为:
ϑ 为大于0 的常数系数,该系数影响因素为货品的包装,根据不同货品实验数据该系数的取值不同。
该式表示在c 层货品的振动加速度。根据文献[8]和文献[11]可得运输时间与振动加速度均对损耗起正向影响,振动加速度受振动传递率的影响,所以包含两要素的损耗函数为关于运输时间的增函数。根据谢丹丹[12]的振动时间实验结果证明在振动频率f0与振动加速度G0相同的情况下,振动损伤量随时间增加而增加,且增长速度随时间变快,即损伤函数的二阶导数大于0,一阶导数大于0。综上,本文初步将第c 层货品振动损伤度函数描述为:
σ 为振动损伤时间敏感因子。关于货品堆放层数c 的计算,运输货品量越大则堆放层数越高,则c 与qi正相关,令c=xqi,x 为一常数,与运输车厢底面面积有关。
通过每一层单个货品的损耗总和求平均数可以得到整车货品的近似损伤量,所以单个需求点货品的损耗量:
则单车损耗的量为:
为简化计算,可将c 用qi替代,则总运输振动损耗为:
2.2 运输中变质损耗成本计算
在冷链运输中,货品发生变质的原因有两部分:运输时间过长导致货品变质产生的货损;运输过程中发生损伤,损伤处与空气接触,加剧变质。根据文献[12]研究表明,受到振动损伤的货品其生理指标以及特性会发生变化,加速其自身的变质速度。
在冷链物流过程中货品新鲜度是衡量货损的主要指标。本文引用于超[13]建立的关于时间的新鲜度函数计算货品的新鲜度ε=2-eθt,则货品关于运输时间的损耗量:
则变质损耗L2可以表示为:
2.3 装卸失温变质损耗计算
丁秋雷等[14]在研究冷藏车冷冻故障时得出农产品新鲜度函数为递减函数:,其中:β 为温度敏感因子且β>0,t0为农产品开始腐败的时间,t0时刻内农产品不发生变质。
在进行装卸工作时,本文假设冷藏车的冷藏设备依然工作,留在车上的货品保持冷藏不在此时产生失温货损。但装卸时由于搬出冷藏车厢的生鲜暴露在常温下,其包装起到的保温作用可以近似视为引文中设备故障时产生的环境。本文设定设备停运后t0时间内货品品质不变,t0与货物开始变质的温度及环境温度有关。
此时,本文中影响货品品质的主要因素在于搬运时间。货品搬运时间与服务点装卸设备、工人搬运速度和生鲜货品量等有关,为了简化计算,本文设定在各服务需求点生鲜货品搬运速度和搬运设备等条件都相同,搬运时间为qi/s,货品留存率受时间影响,所以,本文农产品装卸时失温变质损耗成本L3则可以表示为:
当(qi/ s-t0)>0 时,表明搬运所需要的时间大于产品升温至腐败临界温度需要的时间,产品产生腐败现象,取值为该式计算得出的值,反之则为搬运时间未超过产品升温至腐败临界温度所需要的时间,该式的取值为0。故L3最终表达式为:
2.4 构建目标函数
综合2.1、2.2、2.3 的损耗计算建立以最低损耗为目标的全局损耗模型,记总损耗为L:
以上约束依次为:表示每辆车起止点均为出发点,表示一辆运输车运载上限,表示每个需求点由一辆车满足需求服务,表示车辆数量限制,表示每个需求点都被服务到且仅被服务一次。
3 算例分析
3.1 算法介绍及使用
本文采用遗传算法进行最优解的计算。遗传算法是一种相对成熟的算法,有较好的鲁棒性和实用性。遗传算法的基本步骤如图1 所示。
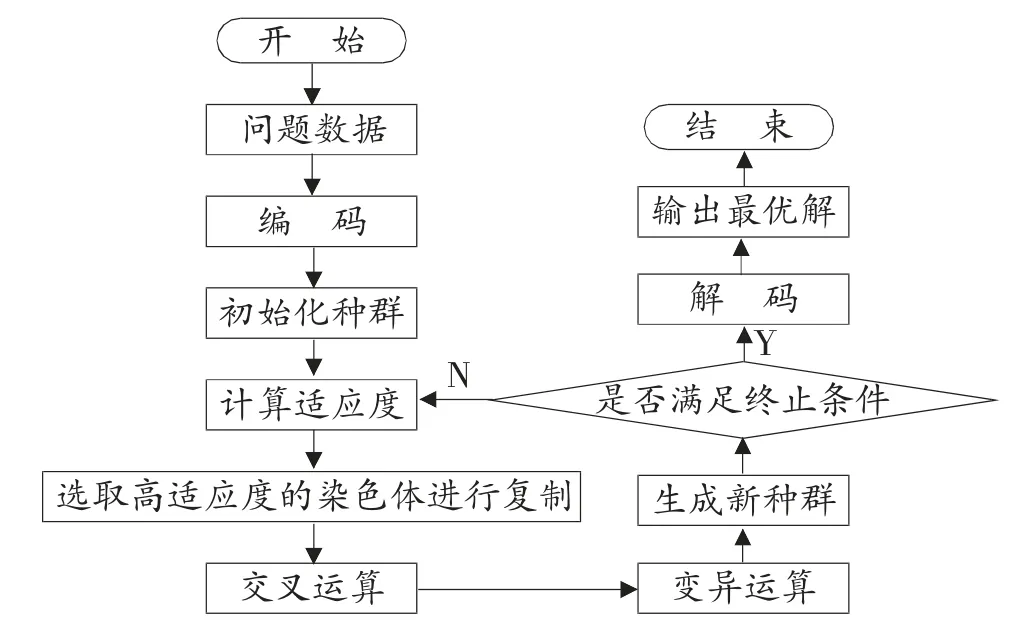
图1 遗传算法基本步骤
遗传算法操作过程简述:
编码。使用自然数编码,染色体长度为需求点个数,将需求点信息写入染色体,再将需求点的需求量以及车辆到达需求点所经过的路程进行累加,设置车辆的最大载额与最大行驶路程,当累加的需求量或行驶路程大于车辆的载额之和最大行驶距离时,记录当前次数,并在当前位置插入0 元素,再从下一个需求点开始继续重复。
初始化种群。随机生成染色体构成初始种群,用作算法出发点。
计算适应度。对初始化的种群进行适应度计算,留存高适应度的染色体,舍弃低适应度的染色体,再随机生成部分染色体补充,重复这一过程直到染色体到达一定规模。
选择运算。用俄罗斯轮盘的概率选择方式选择传到下一代的染色体,适应度高的染色体拥有更高的被选概率。
交叉运算。通过交叉操作可以得到新一代的个体,一般采用单点交叉的方式,确定交叉点,将父代染色体按交叉点相互组合得到子代染色体。
变异运算。在染色体上任意选择两个位置进行互换产生新的个体。该运算的目的在于保证种群多样性并避免局部收敛。
终止条件。在满足遗传代数后,由产生最后一代种群中挑选适应度最高的个体做模型最优解。
3.2 算例数据
本文采用文献[15]的坐标及需求量数据,如表1 所示。
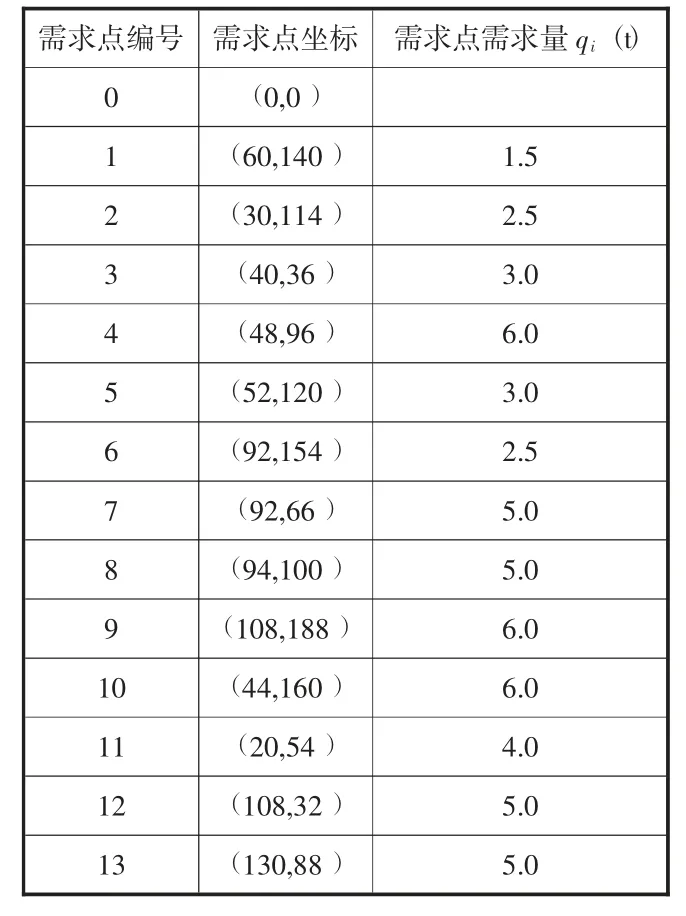
表1 算例分析数据
某物流公司冷库向城中各大型超市运送生鲜产品,使用配送车载重限额Q=12t,配送车数K=5,车辆速度v=60km/h,从冷库装车出发再回到冷库,搬运装卸速度s=2.5t/h。车辆行驶时产生的振动加速度G0=0.15g(g 为重力加速度),ϑ=30,σ=100,θ=0.001 25,t0=0.42h,α=0.3,β=0.15。
3.3 算例求解
利用遗传算法对目标函数进行求解。计算得出考虑振动损伤的易损货品冷链运输模型与不考虑振动损伤的损耗模型算例对比结果如表2 所示。
3.4 结论
经过算例验证可以得出结论,在运输过程中,振动损伤带来的损耗不可忽视,将振动损伤考虑在内进行生鲜冷链运输路径规划可以有效减少物流损失。经过路径规划后,相对于仅考虑变质损伤的路径质量损耗降低了19%,质量提升较为显著。

