基于SVM的我国北部沿岸海上风速估算方法研究*

渠鸿宇 胡海川 黄 彬

国家气象中心,北京 100081

提 要：沿岸海上观测站点稀少,而沿岸陆地观测站点相对密集,开展海陆分布导致的海陆风速差异特征研究,实现由陆地观测风速估算海上风速,有助于提高海上大风预报服务能力。利用我国北方地区两组浮标及其邻近陆地观测站点的2016—2020年逐小时平均风速和阵风风速数据,统计分析海陆风速差异特征及规律,采用支持向量机方法,构建了基于陆地平均风速、陆地阵风风速、海陆站点距离、月份及观测时次的海上风速估算模型。利用另外两组海陆观测站2021年观测数据对估算模型进行检验,结果表明:对于6级及以上的平均风速和7级及以上的阵风风速,模型具有较高的估算准确率,模型估算的两个检验组的海上站点平均风速(阵风风速)RMSE分别为2.40 m·s-1(3.20 m·s-1)和2.35 m·s-1(2.57 m·s-1),较ERA5分别减少了24%(14%)和23%(20%)。在一次温带气旋和冷空气共同影响的大风过程中,模型估算的两个检验组的海上平均风速(阵风风速)平均绝对误差分别为1.6 m·s-1(2.3 m·s-1)和1.1 m·s-1(1.5 m·s-1),在极值时刻的平均风速(阵风风速)误差分别为-1.3 m·s-1(-0.6 m·s-1)和-1.2 m·s-1(-3.1 m·s-1),均优于ERA5计算结果。基于支持向量机的海上风速估算模型能够利用陆地观测风速估算出较为准确的海上大风,可降低海上观测资料不足的影响,具有一定的应用前景。

引 言

海上大风是主要的海洋气象灾害之一(许小峰等,2009),开展海上大风的研究及预报对保证海上作业安全,提高海洋作业效率及减少开支具有重要意义(尹尽勇等,2012)。随着数值模式的飞速发展,海面风场预报取得长足进步(李敏等,2009),但受动力框架、初始场误差、物理参数化方案等因素影响,模式海面风预报与实况仍有一定差距(Toth et al,2001;Mu et al,2002;季晓阳等,2005;胡海川等,2021)。为了进一步提升海上大风预报能力,林良勋等(2004)、吴曼丽等(2012)、薄文波等(2013)、胡波(2019)、潘静等(2022)诸多学者开展了海上大风统计或动力统计预报方法的研究工作,但由于海洋观测资料稀缺,上述方法中多以沿岸、海岛等陆地下垫面观测站数据近似代表海上资料。为进一步提升海上大风预报准确率,应将由下垫面不同所导致的海陆风速差异考虑其中,基于海陆风速差异特征及规律,利用较密集的陆地站点观测风速估算出更真实的海上风速后,再建立海上大风统计或动力统计预报模型。井传才等(1995)、张新玲和吴增茂(1998)和刘京雄等(2004)分析海陆平均风速差异特征及规律,并基于线性、指数及对数函数拟合方法,使用海岛站、石油平台站、船舶站等陆地平均风速估算海上平均风速。但由于海岛站下垫面依然为陆地,石油平台站测风高度过高以及船舶观测资料连续性较差等问题(陈洪滨等,2019),基于上述站点进行海陆风速差异特征研究和建立由陆地风速估算海上风速模型会存在一定不足。浮标观测数据具有连续、实时、可靠的特点(王波等,2014),更适合用来研究海陆风速差异特征,构建由陆地风速估算海上风速模型。另外,相比于平均风速,强阵风更容易造成生命财产损失(Nakamura et al,2007;胡海川等,2022),因此同样需要研究海陆阵风风速差异,并构建海上阵风风速的估算模型。

支持向量机(support vector machine,SVM)是建立在统计学习理论和结构风险最小化原理基础上的机器学习方法,相比传统算法,其在解决小样本、非线性、高维问题中具有特有的优势(丁世飞等,2011),已被广泛应用于降水、雷暴大风、台风等气象要素的预报研究之中(Lin et al,2009;施萧等,2012;钱燕珍等,2012;Nayak and Ghosh,2013;Mercer et al,2013;黄威和牛若芸,2017;杨璐等,2018;Pour et al,2018)。SVM的基本思想是升维和线性化。通过非线性映射函数,把样本空间映射到一个高维的特征空间,使得在高维空间中可以应用线性学习的方法解决原始样本空间中的非线性问题。同时,通过应用核方法(kernel method),无需求解复杂的映射函数即可求得内积,大大减小了计算复杂度。

利用2016—2020年逐小时平均风速和阵风风速数据,选取两组位于我国北部沿岸的浮标和与其邻近的陆地观测站点,研究由海陆分布导致的海陆平均风速和阵风风速差异特征及规律,采用SVM回归方法构建沿岸海上风速估算模型,以实现利用沿岸陆地风速获取较准确的沿岸海上风速。使用另外两组海陆观测站点2021年数据对海上风速估算模型进行检验,验证其在应用中的效果。

1 资 料

本文所用资料包括2016—2021年中国气象局地面实况观测数据中的逐小时风速数据(2 min平均)和小时内极大风速(3 s平均)数据(精度为0.1 m·s-1)。选取曹妃甸浮标站和曹妃甸工业区站记为第一训练组,烟台港浮标站和烟台港务局站记为第二训练组,选取曹妃甸浮标站和曹妃甸零公里国家无人观测站记为第一检验组,董家口浮标站和日照水上运动基地站记为第二检验组(表1),各站点位置如图1所示。其中训练组中的2016—2020年数据(记为训练集)用于特征分析和模型训练,检验组中的2021年数据(记为测试集)用于检验。两组训练组海陆站点直线距离分别为24.4 km、7.7 km,两组检验组的海陆站点直线距离分别为37.6 km、35.4 km,尽量保证了海陆站点受相同的天气系统影响(吕美仲等,2004)。同时,沿岸陆地站点的高度均小于10 m,避免了海拔高度对海陆风速差异研究的影响(赵鸣和苗曼倩,1992)。

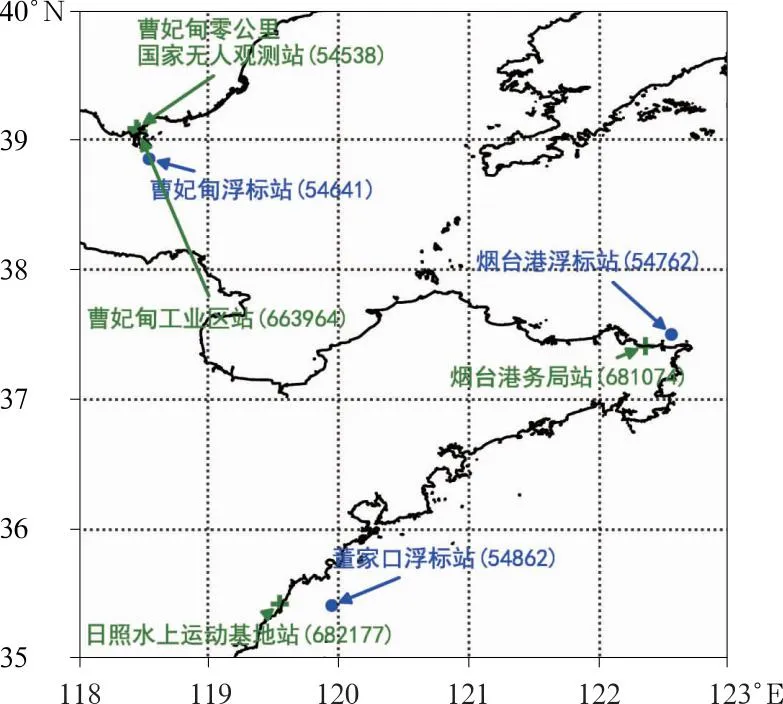
注:蓝、绿色分别为沿岸海上、陆地站点。

表1 训练组站点和检验组站点的名称及站号Table 1 Name and station number of training group and test group

筛选海陆平均风速均大于3级(≥3.4 m·s-1)的情况作为研究对象,共获取成对的海陆平均风速和阵风风速样本14 350对,其中2016—2020年的训练组数据共9809对,2021年检验组数据共4541对。

为横向比较估算模型准确度,采用双线性插值法,将2021年ERA5(Hersbach et al,2018)逐小时的10 m风数据和阵风数据(空间分辨率为0.25° × 0.25°)插值到检验组的海上站点处,进行ERA5风速与海上站点实测风速和模型估测风速的对比分析。

2 差异分析

2.1 整体差异

图2展示了2016—2020年两组海陆站点平均风速和阵风风速的散点分布,图中红色虚线为线性拟合线,k为线性拟合斜率。如图2所示,两组海陆站点中的平均风速与阵风风速的散点均主要集中在对角线左侧,且线性拟合斜率均大于1,表明海上的平均风速和阵风风速均大于陆地。对于同一训练组海陆站点中的平均风速及阵风风速分布而言,平均风速与对角线的偏差更大。两组海陆站点中的平均风速线性拟合斜率分别为1.88和1.48,阵风风速的线性拟合斜率分别为1.32和1.10,表明海陆下垫面的差异对平均风速影响更为显著,而阵风风速的海陆差异相对较小。无论是平均风速还是阵风风速,第二训练组海陆站点的线性拟合斜率均小于第一训练组,平均风速拟合斜率偏小0.4,阵风风速拟合斜率偏小0.21。这可能与海陆站点间的距离有关,距离越近,海陆风速差异有减小的趋势,因此在构建海上风速估算模型中需要考虑到海陆站点距离。

注:黑色虚线:对角线,红色虚线:线性拟合线,k:线性拟合斜率,填色:频次。

无论是海上还是陆地,阵风因子(在时距T0的时间段内持续时间为τ的最大风速与时距为T0的平均风速之比,本文中T0为2 min,τ为3 s)(Monahan and Armendariz,1971),都会随风速的增大呈减小的趋势,但由于下垫面的差异,也会导致阵风因子的差异。通过对比2016—2020年第一训练组海陆站点不同平均风速下的阵风因子可以看出(图3),在不同平均风速下,陆地阵风因子的最大值、最小值、平均值等均大于海上。在平均风速为3级的情况下,陆地阵风因子平均值为2.00,海上则为1.52;在平均风速为6级情况下,陆地阵风因子平均值为1.49,明显大于海上(1.30)。对于相同风速,陆地阵风因子的分布更为离散,平均风速在3～6级时,陆地阵风因子四分位差分别较海上偏大0.15、0.18、0.13和0.06。第二训练组海陆站点的情况与第一训练组基本相同(图略)。海陆分布的差异会导致陆地上平均风速及阵风风速均小于海上。相比于阵风风速,平均风速受海陆分布影响更为显著,因而导致阵风因子的明显差异。相同平均风速情况下,陆地阵风因子更大且分布更为离散。

注:三角:平均值,横坐标括号内数字:样本数。

2.2 季节影响

图4为2016—2020年第一训练组海陆站点在不同季节下平均风速和阵风风速均值及两者比值。如图所示,海上与陆地平均风速和阵风风速的比值均在秋、冬季较大,春、夏季较小,平均风速和阵风风速比值的极差分别为0.61和0.43,表明海陆下垫面差异导致的海陆平均风速和阵风风速差异具有显著的季节变化特征。沿岸陆地风速的季节变化并不显著,平均风速极差仅为0.21 m·s-1,阵风风速极差仅为0.74 m·s-1;而沿岸海上风速具有明显的季节变化,平均风速极差为2.39 m·s-1,阵风风速极差为3.46 m·s-1,显著大于陆地风速极差,海上站点平均风速和阵风风速均在秋、冬季较强,春、夏季较弱,使得海陆风速差异也表现出类似的季节变化。第二训练组海陆站点的情况与第一训练组基本相同(图略)。因此在构建海上风速估算模型中需要加入月份作为预报因子,以提高海上风速估算的准确率。

图4 2016—2020年第一训练组海陆站点(a)平均风速和(b)阵风风速的均值及两者比值的季节变化Fig.4 Seasonal variation of mean value of (a) mean wind speed, (b) gust speed and the ratio of the first training group of sea and land stations from 2016 to 2020

2.3 日变化

图5为2016—2020年第一训练组海陆站点的平均风速和阵风风速均值及两者比值的日变化。如图所示,海上与陆地平均风速和阵风风速的比值均在凌晨偏大,午后偏小,平均风速和阵风风速比值的极差分别为0.73和0.44,表明海陆下垫面差异导致的海陆平均风速和阵风风速差异具有显著的日变化特征。沿岸陆地风速的日变化并不显著,平均风速极差仅为0.22 m·s-1,阵风则仅为0.69 m·s-1;而沿岸海上风速具有明显的日变化,平均风速极差为2.93 m·s-1,阵风则为4.19 m·s-1,显著大于陆地风速极差,海上站点风速较大值出现在凌晨,较小值出现在午后,使得海陆风速比值也表现出类似的日变化。第二训练组海陆站点的情况与第一训练组基本相同(图略)。因此在构建海上风速估算模型时需要加入观测时次作为预报因子,以提高海上风速估算准确率。

图5 2016—2020年第一训练组海陆站点(a)平均风速和(b)阵风风速均值及两者比值的日变化Fig.5 Daily variation of mean value of (a) mean wind speed, (b) gust speed and the ratio of the first training group of sea and land stations from 2016 to 2020

3 估算模型

利用2016—2020年数据建立基于SVM回归方法的海上平均风速和阵风风速估算模型。数据预处理以及模型训练、优化、估算和检验流程如图6所示,其中数据预处理中采用Z-Score标准化方法对连续型估算因子(如平均风速、阵风风速和海陆站点距离)进行标准化处理,使用训练集估算因子的均值和标准差对测试集估算因子进行标准化;离散型估算因子(如月份、时次)均为有序型离散变量,直接使用相应的月份或时次数值表示,无需进行额外的编码以及标准化处理。

图6 数据预处理以及估算模型的训练、优化、估算和检验流程图Fig.6 Flow chart of data preprocessing and training, optimization, estimation and test of estimation model

w·φ(xi)+b=0

(1)

(2)

(3)

(4)

式中:w和b分别为权重向量和频数,φ(x)代表由低维到高维的映射函数,模型求解可表示为在限制条件[式(3)和式(4)]下,求解损失函数[式(2),其中C为超参数]最小。式(2)中的第一项为权重系数的L2范数,在确定的ε下,其尽可能的小可允许更多的样本误差小于ε;C用来调节对偏差大于ε样本点的惩罚程度,C越大,模型对这些离散点越敏感,会提高训练集准确度,但容易过拟合,泛化能力差。

SVM回归模型的训练和预测需要计算升维后向量的内积,使用核方法可实现隐式求解高维向量内积,大大减小了计算的复杂度。SVM回归模型常用的核函数有线性核函数、多项式核函数和径向基核函数(又名高斯核函数)。线性核函数具有参数少、速度快的优势,但无法实现升维,主要用于线性可分的问题。多项式核函数和径向基核函数都能实现升维从而解决非线性问题,但前者由于参数多(三个),学习复杂度高。相比而言,径向基核函数参数较少(仅一个超参数),可隐式计算被映射到无限维空间的两个向量的内积,是应用最广泛的核函数。由于使用陆地风速估算海上风速并非简单的线性过程(刘京雄等,2004),因此SVM回归模型采用径向基核函数,如式(5)所示。

K(x1,x2)=e-γ||x1-x2||2γ>0

(5)

式中:x1,x2表示原始样本空间中的任意两个样本的输入向量,γ为超参数,其中γ越大,高斯核函数变化越剧烈,模型对噪声样本越敏感,越容易过拟合。

为找出最优的超参数(核函数超参数γ、惩罚项C和损失距离ε),结合贝叶斯优化的最佳参数智能搜索方法,使用交叉验证法(Kohavi,1995)(取2016—2020年训练组数据的其中一年作为验证集,其余4年为训练集,重复5次),以所有验证集的均方根误差(root mean square error,RMSE)作为评估指标,对超参数进行优化,从而得到最终优化后的模型。

为了找出最优的估算因子组合,结合上述的差异特征分析,使用表1所示的估算因子组合,分别建模,并使用交叉验证法寻求最优超参数,各模型所有验证集的RMSE如表2所示(按平均风速RMSE降序排序)。

表2 以不同估算因子组合构建模型的平均风速和阵风风速估算的RMSE(单位:m·s-1)Table 2 The root mean square error of the mean wind speed and gust speed of all validation sets of the model constructed with different combinations of estimation factors (unit: m·s-1)

从表2中可以看出,无论是平均风速还是阵风风速估算模型,仅使用沿岸陆地平均风速估算海上风速的RMSE(平均风速RMSE为2.577 m·s-1,阵风风速RMSE为3.220 m·s-1)均高于仅使用沿岸陆地阵风风速估算海上风速的RMSE(平均风速RMSE为2.293 m·s-1,阵风风速RMSE为2.684 m·s-1),这与上文分析得到的海陆下垫面的差异对平均风速影响更为显著,而阵风风速的海陆差异相对较小相对应;当模型同时使用陆地平均风速和阵风风速作为预报因子组合时,平均RMSE较模型仅使用一个要素时均有所降低,说明应同时考虑陆地平均风速和阵风风速。在使用以上估算因子组合基础上,逐步增加海陆站点距离、月份以及时次分别建模,三个模型验证集RMSE均有进一步降低,平均风速RMSE分别为2.079、1.980、1.738 m·s-1,阵风风速RMSE分别为2.497、2.204、2.044 m·s-1,这进一步说明了海陆风速差异与海陆站点距离存在相关性,且具有季节和日变化,在估算因子中增加海陆站点距离、月份以及时次可进一步提高估算模型的准确率。

综上所述,最佳估算因子组合为沿岸陆地平均风速及阵风风速、海陆站点距离、月份、时次,使用该估算因子组合,构建的平均风速估算模型的超参数C为2.030,γ为0.206,ε为0.446,构建的阵风风速估算模型的超参数C为2.095,γ为0.164,ε为0.113。

4 检验评估

4.1 误差检验

由于海上大风较高的破环力,是海上风预报服务和研究的重点,因此误差检验仅针对6级及以上的平均风以及7级及以上的阵风(按海上风分级)。图7为两个检验组海上站点6级及以上平均风速和7级及以上阵风风速的模型估算的与ERA5计算的相对误差散点分布。由图可见,平均风速和阵风风速的相对误差散点的横坐标值均整体小于纵坐标值,且较多的样本点位于对角线之上。对于两个检验组的海上站点,ERA5计算的平均风速的平均相对误差分别为20.2%和18.1%,而模型估算的分别为13.9%和14.6%;ERA5计算的阵风风速平均相对误差分别为15.1%和13.6%,而模型估算的分别为13.6%和12.4%(表3);模型估算的平均风速相对误差较ERA5小的样本点占比分别为73.5%和63.0%,模型估算的阵风风速则分别为57.0%和53.0%。

图7 2021年模型估算与ERA5计算的(a,b)6级及以上平均风速和(c,d)7级及以上阵风风速的相对误差散点分布(a,c)第一检验组,(b,d)第二检验组Fig.7 Scatter diagram of relative errors estimated by the model and ERA5 for the (a, b) mean wind speed ≥ scale 6 and (c, d) gust speed ≥ scale 7 in 2021(a, c) the first test group, (b, d) the second test group

表3 2021年模型估算与ERA5计算的6级及以上平均风速和7级及以上阵风风速的RMSE和平均相对误差Table 3 Root mean square errors and mean relative errors estimated by the model and ERA5 for the mean wind speed ≥ scale 6 and gust speed ≥ scale 7 in 2021

对于两个检验组海上站点6级及以上的平均风速,ERA5的RMSE分别为3.16 m·s-1和3.05 m·s-1,模型估算的RMSE分别为2.40 m·s-1和2.35 m·s-1,相较于ERA5计算结果,模型估算海上平均风速RMSE分别减少了24%和23%(表3);对于两个检验组海上站点7级及以上的阵风风速,ERA5的RMSE分别为3.70 m·s-1和3.21 m·s-1,模型估算的RMSE分别为3.20 m·s-1和2.57 m·s-1,相较于ERA5计算结果,模型估算的阵风风速RMSE分别减少了14%和20%(表3)。

进一步对6级及以上的平均风速以及7级及以上的阵风风速进行分级检验,检验结果如图8所示。由图可见,无论是ERA5计算还是模型估算结果在大部分风级下均较实测偏小,但模型估算的平均误差较ERA5计算更接近于0 m·s-1。在不同风级下,模型估算的两个检验组海上站点的平均风速的平均误差为-2.32～0.38 m·s-1,阵风风速的平均误差为-3.14～0.92 m·s-1,而ERA5计算的平均风速的平均误差为-4.77～-1.80 m·s-1,阵风风速的平均误差为-5.94～-1.39 m·s-1。同时,对于大多数风级,模型估算的海上风速的RMSE均较ERA5偏小,在不同风级下,前者估算的海上平均风速RMSE为2.25～2.79 m·s-1,阵风风速RMSE为2.54～3.67 m·s-1。

图8 2021年ERA5计算和模型估算的(a,b)平均风速和(c,d)阵风风速在各风级下的(a,c)平均误差和(b,d)RMSEFig.8 (a, c) Mean error and (b, d) RMSE of (a, b) mean wind speed and (c, d) gust speed calculated by ERA5 and estimated by model under different wind scales in 2021

综上所述,对于6级及以上的平均风以及7级及以上的阵风, SVM回归模型估算的海上风速具有较高的准确率,且优于ERA5计算结果,可见该模型能较好地估算出海上大风。

4.2 个例对比

2021年11月21—22日(北京时,下同),受冷空气和温带气旋的共同影响,渤海、渤海海峡、黄海、东海、台湾海峡、台湾以东洋面、巴士海峡、南海北部海域、北部湾出现了8～9级、阵风10级的大风(聂高臻和黄彬,2022)。

图9为两个检验组在21日12时至22日12时实测到的风速时间序列,可以看出,海陆风速差异明显,且模型估算的海上风速较ERA5计算更接近实测。对于第一检验组,海上实测的平均风速和阵风风速均值分别为15.8 m·s-1和21.5 m·s-1,远大于其对应的陆地站点实测风速,模型估算的平均风速和阵风风速平均绝对误差分别为1.6 m·s-1和2.3 m·s-1,较ERA5(分别为3.4 m·s-1和4.9 m·s-1)偏小。此次过程的最大平均风速和阵风风速出现在21日20时,分别为21.4 m·s-1和25.9 m·s-1,同一时刻模型的估算偏差分别为-1.3 m·s-1和-0.6 m·s-1,小于ERA5在此时的风速偏差(分别为-6.9 m·s-1和-5.0 m·s-1)。对于第二检验组,模型估算的风速同样整体优于ERA5,前者平均风速和阵风风速平均绝对误差分别为1.1 m·s-1和1.5 m·s-1,后者为2.1 m·s-1和1.8 m·s-1,在最大风速时刻(21日23时),前者的平均风速和阵风风速误差为-1.2 m·s-1和-3.1 m·s-1,后者为-3.2 m·s-1和-3.6 m·s-1。综上所述,SVM回归模型估算风速较准确地反映了此次冷空气和温带气旋造成的两个检验组海上站点的大风风速变化,且准确率整体优于ERA5。

图9 2021年11月21日12时至22日12时(a,b)第一检验组和(c,d)第二检验组站点的陆地实测风速、海上实测风速、ERA5风速以及模型估算风速对比(a,c)平均风速,(b,d)阵风风速Fig.9 Comparison of the measured land wind speed, the measured sea surface wind speed, ERA5 wind speed and the model estimated wind speed of (a, b) the first and (c, d) the second test groups from 12:00 BT 21 to 12:00 BT 22 November 2021(a, c) mean wind speed, (b, d) gust speed

5 结论与讨论

利用位于我国北部沿岸的两组浮标及其邻近陆地观测站2016—2020年逐小时平均风速和阵风风速数据,统计分析了海陆风速差异特征及规律,基于SVM回归方法,使用沿岸陆地平均风速及阵风风速、海陆站点距离、月份、时次作为估算因子组合,构建了沿岸海上平均风速和阵风风速估算模型,并使用另外两组海陆站点的2021年数据对估算结果进行检验。主要得到以下结论:

(1)海陆下垫面差异对平均风速分布的影响显著大于阵风风速,两组站点的海陆平均风速的线性拟合斜率分别为1.88和1.48,海陆阵风风速拟合斜率分别为1.32和1.10;海陆风速差异具有显著的季节变化和日变化,第一训练组站点,不同季节的海陆平均风速和阵风风速比值极差分别为0.61和0.43,不同时次的海陆平均风速和阵风风速比值极差分别为0.73和0.44,第二训练组情况类似;另外,相同平均风速情况下,陆地阵风因子较海上阵风因子更大且分布更离散。

(2)使用2021年两个检验组数据对模型估算结果进行检验发现,对于6级及以上的平均风速和7级及以上的阵风风速,模型具有较高准确率,且优于ERA5计算结果。对于两个检验组海上站点6级及以上的平均风速,模型估算的RMSE分别为2.40 m·s-1和2.35 m·s-1,相较ERA5分别减少了24%和23%;对于两个检验组海上站点7级及以上的阵风风速,模型估算的RMSE分别为3.20 m·s-1和2.57 m·s-1,较ERA5分别减少了14%和20%。对一次温带气旋和冷空气共同影响的大风过程进行检验发现,模型估算风速较准确地反映出了两个海上站点的大风风速变化。此次过程中,模型估算的两个检验组海上站点的平均风速的平均绝对误差分别为1.6 m·s-1和1.1 m·s-1,阵风风速平均绝对误差分别为2.3 m·s-1和1.5 m·s-1,均优于ERA5计算结果。

通过一系列分析,本文统计了海陆下垫面差异导致的海陆风速差异特征及规律,并使用SVM回归模型,以沿岸陆地平均风速及阵风风速、海陆站点距离、月份、时次为估算因子组合,较准确地估算了沿岸海上大风。为使用丰富的沿岸陆地风速观测数据推测沿岸海上大风,从而弥补海上观测资料不足,提供了一种可靠、便于应用的方法。值得注意的是,受制于海上观测资料有限,以及海陆站点距离和海拔高度的要求,本文选取的站点均位于我国北部沿岸,因此研究结论仅适用于我国北部沿岸地区。另外,基于统计结果,将月份、时次作为离散的分类型预报因子加入模型中并不具备物理意义。随着海上观测数据的不断丰富,后期可开展我国近海其他海区的海陆风速差异特征研究,并进一步分析不同天气系统下的海陆风速差异特征,深入分析其背后的物理机制,结合物理机制和统计学规律,构建针对我国近海全海域且更加准确的估算模型。