计及连锁跳闸的多目标最优潮流模型
罗杰,李晨晨,叶祖火
(1.国网福建省电力有限公司永安市供电公司,福建 永安 366000;2.福建理工大学,福建 福州 350100;3.福建水利电力职业技术学院,福建 永安 366000)
一直以来,电力系统最优潮流(optimal power flow,OPF)是保证电力系统安全性和经济性的重要方式。随着电网结构日益复杂,系统运行日渐逼近其稳定极限,以往单一目标的OPF已无法满足智能电网的需求,而多目标OPF因能够有效协调系统中多个不同重要性的目标,受到国内外研究人员的广泛关注。
截至目前,研究人员对于电力系统OPF已进行了广泛探讨:文献[1]考虑系统灵活性与经济性,构建一种基于概率的电力系统灵活性资源OPF模型;文献[2]考虑风电的不确定性,构建基于潮流控制器的松弛型OPF模型;文献[3]考虑了安全裕度和发电成本的发电权交易多目标优化模型;文献[4]提出考虑电压安全裕度的OPF模型;文献[5]以系统发电成本指标、损耗指标、性能指标为目标函数,构建一种多目标OPF模型;文献[6]分析了电压安全成本与负荷的最优关系,建立考虑电力系统发电成本和负荷裕度的多目标OPF模型;文献[7]利用可控移相器原理接入系统的等效功率注入模型,以系统有功网损为目标函数,构建一种含可控移相器的OPF模型;文献[8]通过改良网损等值负荷的求解方式优化半线性化模型,构建基于改进网损等值负荷的直流OPF模型;文献[9]构建了一种新型线性化动态OPF模型,通过解耦、代换推导、热启动对传统交流OPF模型进行线性处理,构建新型线性化动态OPF模型;文献[10]针对传统暂态稳定约束OPF模型,将目标函数和相关约束条件做模糊化处理,以此构建以求解满意度最大化的暂态稳定约束OPF模糊新模型;文献[11]结合新型能源和传统电源特性,构建了基于线性规划算法的源-网-荷互动OPF模型。上述研究虽然从静态和暂态角度建立OPF模型,但是都未明确考虑连锁跳闸现象。文献[12]考虑正常状态和N-1状态下的静态安全相关约束,构建了基于负荷转供的OPF模型;文献[13]基于机会约束模型构建考虑连锁跳闸运行风险的OPF模型,该模型能求取不仅满足系统常规安全约束而且满足连锁故障风险机会约束的最优经济出力。这些研究虽然考虑了连锁跳闸条件,但未与保护的动作行为相结合,不利于反映真实的连锁故障触发。
实际上,在电力系统的各种安全问题中,连锁跳闸是一种容易忽视但却极有可能引起严重停电事故的问题。针对此,本研究从电力系统连锁跳闸的角度出发,考虑发电运行成本和安全裕度2个目标构成目标函数,以及节点电压、线路传输功率等相关约束条件,建立考虑连锁跳闸的电力系统多目标OPF模型;利用粒子群优化(particle swarm optimization,PSO)算法找到发电成本投入和安全裕度之间的最优解,以求得满足2个目标函数最优的电网稳定运行状态。最后通过 MATLAB软件进行仿真分析,验证所提方法的有效性,为实现电力系统多目标OPF提供理论依据。
1 考虑电网对于连锁跳闸安全性的OPF模型
1.1 OPF基本模型
OPF要求满足在复杂的电力系统运行和安全约束条件下,通过调整系统中可控变量来实现预期目标最优的稳定运行状态。OPF的基本模型可表示为
(1)
式中:F为OPF的目标函数,其与控制变量u和状态变量x有关,min表示最小值;g(u,x)和m(u,x)分别为不等式约束和等式约束的缩写形式;f为给定的用来描述系统运行效益的某一目标函数。
一般情况下,OPF的目标函数会因研究目的不同而有所不同。本研究重点考虑电网对于连锁跳闸的安全裕度,以及电网的安全性和经济性,所以综合考虑电网对于连锁跳闸的安全裕度以及发电成本来构建相应的目标函数。
1.2 电网对于连锁跳闸的安全性
关于连锁跳闸的电网安全性,本文借鉴文献[14-15]提出的计算电网安全裕度的方法。在经过潮流计算后,比较所有线路的后备保护测量值与整定值,定义式(2)来衡量当前电网的安全水平:
Ib,mist=|Ib,set|-|Ib|.
(2)
式中:Ib,set和Ib为由线路Lb后备保护配置及其动作方程决定的变量,Ib,set为电流保护定值,Ib为线路Lb的电流测量值;Ib,mist为线路Lb中用以衡量电流动作值与整定值之间电气距离的变量,当Ib,mist≤0时,线路Lb被后备保护切除,Ib,mist>0时,线路Lb不会被后备保护切除。本文为线路配置电流型后备保护,如果同时考虑剩余所有线路,利用式(3)进一步给出评价当前电网安全裕度水平的指标:
D=minIb,mist.
(3)
式中D为电网的当前运行状态与连锁跳闸临界运行状态之间的距离,是系统中所有线路Ib,mist最小值,用来评价系统的安全裕度水平。D<0时,电网发生连锁跳闸;D=0时,电网处于连锁跳闸的边界;D>0时,电网不会发生连锁跳闸。D越大,电网越不易发生连锁跳闸,即电网的当前运行状态与连锁跳闸临界运行状态之间的距离越远。
1.3 考虑连锁跳闸的电网经济性
本文假定调整时间充足的情况下,以发电机调整有功出力成本为经济目标,定义系统发电成本[16]
(4)
式中:PGi为发电机i的有功出力;k1i、k2i、k3i均为系统发电成本系数;E为参与调整的发电机集合。
1.4 计及连锁跳闸的OPF模型
基于前述分析,构建以系统发电成本与安全裕度的多目标函数
(5)
式中w1和w2分别为2个子目标函数的权重系数,且w1+w2=1。因为本文所建最优模型是以发电成本最低和安全裕度最高为目标,为了统一2个子目标的变化方向,将安全裕度D值设为倒数的形式,同时为了避免出现D=0(无解)的情况,在分母加上1个很小的正数α。
本研究主要针对系统发生1次跳闸的初期阶段,所以必须保证系统初始故障前后均满足一定的等式约束和不等式约束。约束条件如下[17]:
(6)
式中:r为初始故障数,最大初始故障数为N;PGi,r、QGi,r分别为第r个初始故障前后系统中第i台发电机的有功出力和无功出力;PDi,r、QDi,r分别为第r个初始故障系统中节点i的注入有功功率和无功功率;PGi,min、PGi,max分别为第i台发电机有功出力的下限和上限;QGi,min、QGi,max分别为第i台发电机无功出力的下限和上限;Pij,r为线路Lb传输的有功功率,Pij,max为线路Lb传输的有功功率限值;Ui,r为第r个初始故障前后节点i的电压,Ui,min为节点i的电压下限,Ui,max为节点i的电压上限;Gij、Bij分别为节点i、j(其中i表示发电机节点,j表示负荷节点)对应导纳矩阵的实部和虚部;n为电网中的节点集合;θij,r=θi,r-θj,r,其中θi,r、θj,r分别为第r个初始故障前后系统中节点i、节点j的电压相角。
若发生N个初始故障后,则将式(6)的约束条件扩充为N组,每组式(6)形式的约束条件对应1个初始故障。进一步将故障前后的不等式约束和等式约束分别简写成gr(x)≥0和mr(x)=0,其中,等式约束为功率平衡约束,不等式约束为发电机有功出力和无功出力约束、节点电压约束、线路传输功率约束。
综合上述分析,计及连锁跳闸的多目标OPF模型可表示为:
(7)
1.5 预想初始故障筛选
电网发生初始故障后,应采用精确的潮流计算方法计算各线路的电流,此时式(3)中的D表示为除去初始故障线路以外剩余线路中Ib,mist的最小值,根据D值可以评价故障线路的严重性[16-18]。在满足约束条件下,计算断开初始故障后的D值,若D≤0,系统可能发生连锁跳闸,D>0则系统正常运行。对于每个初始故障,只要剩余任何1条线路满足D≤0的条件,就将该初始故障送入预想初始故障集S1。
之所以要筛选出1组预想初始故障集,是因为本文建立的OPF模型也是1种连锁跳闸的预防控制措施,并通过计算OPF调整后的安全裕度来判定预防控制的好坏。
2 基于PSO算法的模型求解
PSO是基于鸟群觅食的随机寻优算法,其具有依赖经验参数少、收敛速度快、优化性能良好等优点,适合求解需要满足一定精度和速度要求的电力系统组合优化问题[18]。其迭代公式如下:
(8)
式中:vk,h和xk,h分别为第h次迭代时粒子k的速度和位置;gbest和Pk,best分别为粒子k的最佳位置和种群最佳位置;w为压缩因子;c1、c2为加速因子,通常取c1=c2=2;r1、r2为介于0~1之间的随机数。
本文在求解约束问题时引入外惩罚函数法,该方法利用目标函数和约束函数构造带有参数的增广目标函数,将约束问题转化为一系列无约束问题,进而用无约束方法来求解约束问题[19]。根据式(7)进一步构造如下惩罚函数:
(9)
式中:εc和βe分别为式(6)中第c个不等式和第e个等式的惩罚因子,二者值均设为0.01。
利用式(9)给出的惩罚函数,待优化变量为发电机有功出力。本文结合PSO算法将给出如下的具体算法流程:
步骤1,读入系统数据,设置粒子种群数和最大迭代次数。
步骤2,初始化粒子群,并随机产生多个粒子,赋予每个粒子初始速度和初始位置。
步骤3,根据式(8)更新粒子的速度和位置向量。
步骤4,计算目标函数和惩罚函数,通过比较最佳适应度来更新个体最优解和种群最优解。
步骤5,判断是否达到最大迭代次数。若未达到,则转入步骤3,继续进行迭代;若达到,则计算结束,输出最优解。
3 算例分析
本文利用IEEE 39节点系统对所提方法进行验证,系统接线如图1所示,系统各发电机的成本系数值见表1。设该系统中节点31为平衡节点,平衡节点的量不作为系统的状态变量。

表1 发电机的成本系数Tab.1 Generator cost coefficients
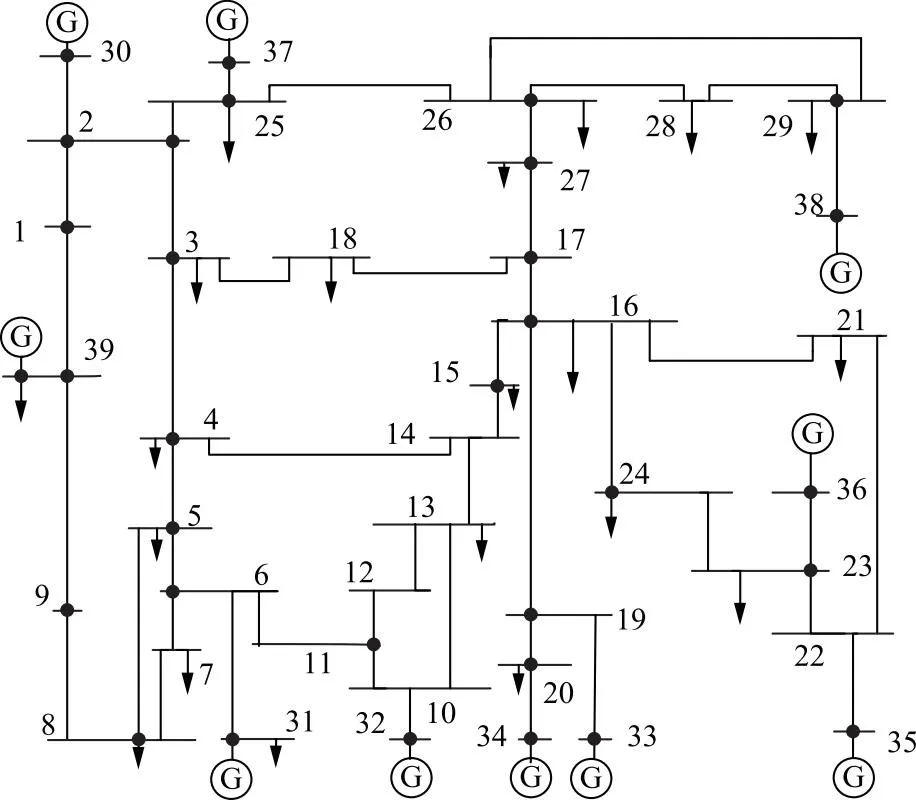
图1 IEEE 39节点系统Fig.1 IEEE 39 node system diagram
采用MATLAB软件对所提方法编程求解,系统各元件数据均以标幺值表示,其中功率基准值设为100 MVA。系统后备保护以电流型保护为例,电流保护定值采用虚拟数据,每条线路定值均设为5.2 kA。发电成本和安全裕度也均以标幺值表示。
设置粒子种群数为50,最大迭代次数为200,本研究认为发电成本与安全裕度对于系统同等重要,因此权重系数均设为0.5,其目标函数值中的发电运行成本和安全裕度随迭代次数变化的过程曲线如图2、图3所示。

图2 发电成本变化曲线Fig.2 Variation curve of power generation cost
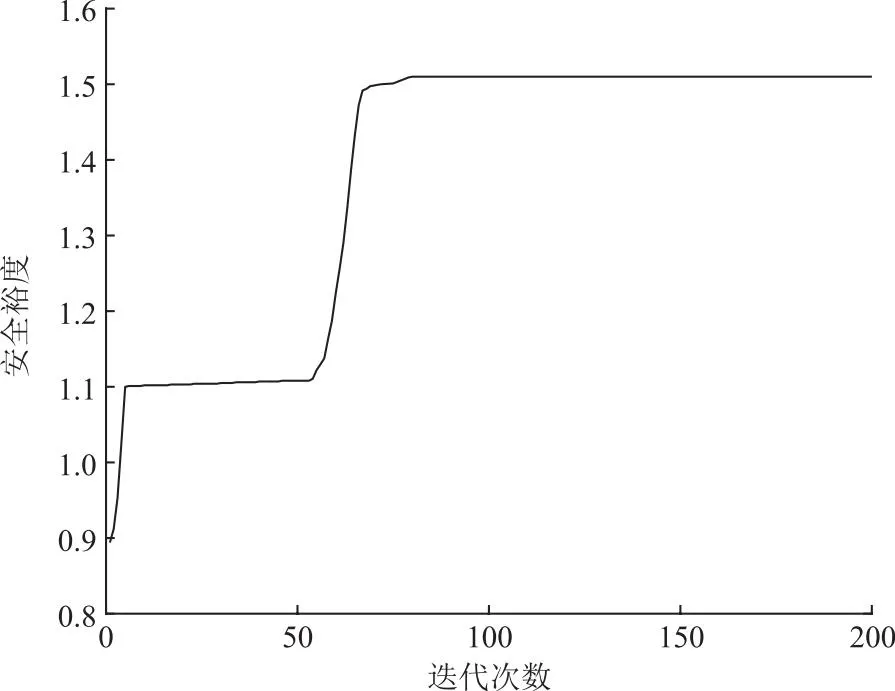
图3 安全裕度变化曲线Fig.3 Variation curve of safety margin
IEEE 39节点系统计算出的最优解取值:电网安全裕度为1.51,发电运行成本为13 843。由图2和图3可以看出随着迭代次数增加,目标函数中的发电运行成本和安全裕度都能逐渐逼近最优值。图4所示为发电运行成本和安全裕度的关系曲线,由图4可知发电运行成本和安全裕度大致呈现反比例关系,即系统不仅能满足发电运行成本降低,还能提高电网对于连锁跳闸的安全裕度,由此说明本文方法具有一定可行性。

图4 发电成本与安全裕度的关系曲线Fig.4 Relationship curve between power generation cost and safety margin
图5所示为各发电机节点调整前后的有功出力对比,通过曲线可以观察到系统在目标函数最优时的发电出力变化情况。
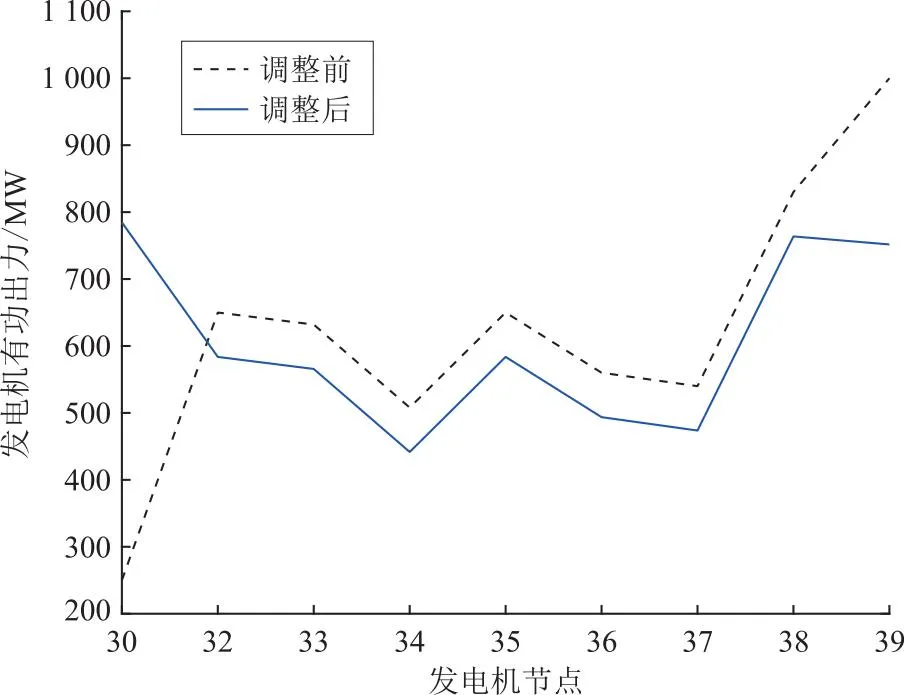
图5 发电机节点有功出力调整前后变化曲线Fig.5 Change curves of active power output of generator nodes before and after adjustment
为了验证计及连锁跳闸的最优潮流模型(optimal power flow model considering cascading trip,OPFMCCT)的防御效果,对各线路进行开断模拟。采用前述方法筛选出的预想初始故障集S1中的线路:L21-22(介于节点21和节点22之间的线路)和L23-24(介于节点23和节点24之间的线路)。采用PSO算法得到的潮流数据分别去重新计算初始故障L21-22和L23-24开断后系统剩余各线路的电气量,按式(3)计算考虑连锁跳闸的电网安全裕度D值,从而判断OPFMCCT的预防控制效果。发电机调整前后的安全裕度D值见表2。

表2 调整前后安全裕度值Tab.2 Safety margin values before and after adjustment
经过多次测试,基于OPFMCCT调整发电机有功出力后,此时系统处于更加安全的运行状态,计算预想初始故障发生后的安全裕度指标均有不同程度的提升,验证了OPFMCCT对连锁跳闸的预防效果。若经过优化后,考虑连锁跳闸的安全裕度指标D值仍然小于0,则说明当前电网可能会发生连锁事故,需要采取紧急控制措施,对于这种情况,本文暂不考虑。
4 结论
本文建立了一种计及连锁跳闸的多目标OPF模型,其实质上也是一种预防控制模型。通过调整发电机有功出力,以发电成本和安全裕度为目标函数,结合PSO算法得到系统的OPF分布。通过分析,得到以下结论:
a)在分析连锁跳闸表现形式的基础上,结合继电保护后备保护的动作行为,给出能体现电网对于连锁跳闸安全性的指标,更加贴合实际电网。
b)本文提出的OPFMCCT既能保证发电成本的降低,同时兼顾了电网对于连锁跳闸的安全裕度。
c)对于初始故障的选取,通过安全裕度值初步筛选出容易引发故障的线路,有利于后续针对此线路采取相应控制措施。
d)通过算例分析,在PSO算法得到的最优初始运行状态下,系统面对连锁跳闸威胁时仍具有一定的安全裕度。说明OPFMCCT能有效提高电网对于连锁跳闸的防御能力,对从源头上预防连锁跳闸具有重要意义。
本文方法虽然具有一定的可行性,但是在计及连锁跳闸时只考虑用安全裕度指标去检验OPFMCCT的预防控制效果,检验手段略显单一。如何综合考虑事故风险与控制中其他经济代价等因素来衡量OPFMCCT的预防控制效果,是下一步的研究方向。

