计及车载储能的牵引网有功协调运行与网压波动抑制策略

苏照旭，甘永忠，田铭兴，刘源涛

(1.兰州交通大学 a.自动化与电气工程学院；b. 甘肃省轨道交通电气自动化工程实验室，甘肃 兰州 730070；2.中国铁路兰州局集团有限公司供电部，甘肃 兰州 730030)

随着机车牵引功率、行车密度以及供电区段的不断增大，牵引供电系统面临日益严峻的挑战。特别是在复杂地势条件下，机车经常面临频繁的重载和制动工况，这些工况导致了机车端网压的显著波动，对供电质量产生了严重的负面影响。这些波动可能引发机车牵引变流器的封锁和停车，进而扰乱行车秩序，对轨道交通系统的稳定性和可靠性构成威胁。

在这一背景下，能量存储装置被认为是一种有力的解决方案，可以对再生制动能量进行存储利用，减少牵引变电所出力，抑制网压波动[1]。牵引负荷是一种冲击负荷且具有较强随机性，为满足需求，超级电容更适合作为交流电气化铁路中网压波动抑制的储能元件。文献[2]提出一种长大坡道线路中的车载储能网压波动抑制方案，但并未提出最优的储能控制策略。文献[3]提出了一种基于模块化多电平变换器的车载超级电容储能系统综合控制策略，但仅仅是针对城市轨道交通系统。

基于储能主动参与的牵引网网压波动抑制策略的成功实施需要精确的牵引网潮流分布计算结果。文献[4]证明了电热耦合效应对配电网潮流的显著影响，而基于恒定电阻的潮流计算方法可能导致较大的误差。文献[5]中的方法将电热耦合效应扩展到牵引供电系统，并在潮流计算过程中通过温度修正电阻参数，经过多次迭代计算，获得了机车端更为准确的网压计算结果，研究结果表明，导线电流和环境参数的变化对牵引网等效阻抗和潮流计算产生了不可忽略的影响。文献[6]在电热耦合理论的基础上基于改进的GM(1，1)模型对牵引网输电导线载流量进行预测，打破了牵引网载流量是固定值的传统认知，进一步对载流量进行短期预测，从而为牵引网调度提供技术支持并充分挖掘牵引网输电导线的载流能力，并得到牵引网电气参数受牵引网架设沿线的地理气候条件的影响明显的结论。

由于车载储能系统的接入给牵引网运行调度带来了新的挑战，且牵引网本质上是一种“特殊”的配电网[7]，因此本文借鉴配电网最优潮流相关研究对车载储能系统进行运行控制。文献[8]指出由于配电网潮流约束的非线性特征，本质上车载储能系统运行控制为非线性规划。基于人工智能的启发式算法因其简单、可暴力求解复杂问题的优势，得到了广泛的应用。而智能算法在求解非线性优化模型时容易出现陷入局部最优、求解速度较慢等问题。因此，越来越多的学者开始探索有效的数值分析法，提高非线性问题的求解速度，并保证结果最优，适应配电网运行规划的要求。文献[9-10]首次系统性地建立了以Distflow[11]为基础的支路潮流模型，来求解最优潮流问题。此外，在配电网规划运行优化模型中，不可避免会出现离散变量，离散变量将会给模型求解带来一定的难度，混合整数编程(mixed integer programming，MIP)建模，特别是一些商业软件或算法包的出现良好地解决了该问题，如 CPLEX、GUROBI 等，其在配电网运行规划中均得到了广泛应用[12-13]。

因此，为了有效解决机车端网压不稳定的问题，本研究在电热耦合理论的基础上深入研究考虑牵引网架设沿线的地理气象参数的牵引供电系统最优潮流；基于车载超级电容电力机车框架，提出一种机车端网压波动抑制策略，该策略可在更为精确的潮流分布计算结果下，为机车储能控制系统提供准确的网压波动抑制方案；最后通过算例进行详细的分析与论证，以验证本文所提方法的正确性和可行性。

1 计及线路电阻随温度变化影响的牵引网最优潮流

1.1 牵引网基本结构

图1 等效电路模型Fig.1 Equivalent circuit model

本文以单线直供方式为例，牵引网等效阻抗计算方法参考文献[14]。单位长度牵引网等效阻抗Z可表示为：

(1)

式中：ZC为接触线单位长度自阻抗；ZT为钢轨单位长度自阻抗；ZCT为接触线与钢轨单位长度互阻抗。

图1中节点g和h(g+1)间等效阻抗Zg可表示为：

(2)

式中：Zg为节点g和h(g+1)间等效阻抗；lh和lg分别为机车h至牵引变电所的距离和机车g至牵引变电所的距离。

1.2 温度变化与导线电阻的关系

牵引网输电导线的温度决定其输电能力。为了导线的安全运行，导线温度不得超过其设计规程的要求，以免造成导线的损坏，影响供电安全。导线温度不是一个恒定值，取决于导体内部产生的热量与其表面热交换之间的能量平衡，这种热交换主要受到导线与环境的温差以及风速、风向角、海拔高度和太阳辐射强度等外部环境的影响。通过考虑输电导线焦耳热、对流散热、辐射散热以及太阳辐射吸热，建立牵引网输电导线电热耦合模型。根据IEEE-738标准，输电导线的热交换过程满足式(3)所示的暂态热平衡方程[15]。

(3)

式中：t为时间；R为温度Ts时输电导线的电阻；M为单位长度输电导线质量；Cp为输电导线材料的比热容，单位 J/(kg·℃)；I为输电导线电流有效值；Ts为输电导线运行温度；qc为单位长度输电导线对流散热功率；qr为单位长度输电导线辐射散热功率；qs为单位长度输电导线太阳辐射吸热功率。

输电导线电阻R与温度Ts的关系为

R(Ts)=R20[1+αl(Ts-20)].

(4)

式中：R20为单位长度输电导线在20 ℃下的电阻值；αl为电阻温度系数，单位 ℃-1。

对流散热功率qc、辐射散热功率qr和太阳辐射吸热功率qs满足式(5)—(7)：

qr(Ts)=1.78D0ε[(Ts+273)4-(Ta+273)4]×10-9，

(5)

qs=αQsesin(θ)A，

(6)

(7)

式中：Kangle为风向系数；D0为导体半径；ρf为空气密度，单位 kg/m3；Vw为风速；μf为空气动态黏度，单位 kg/(m/s)；kf为空气导热系数，单位 W/(m·℃)；Ta为导线所处环境温度；ε为辐射率，无单位；α为导体吸热系数；Qse为日照辐射强度，单位 W/m2；θ为太阳有效入射角度；A为单位长度输电线路有效投影面积；其中Kangle、ρf、μf和Qse的计算公式详见参考文献[7]。

当输电导线的吸热与散热达到动态平衡时，式(3)变为：

I2R(Ts)+qs=qc(Ts)+qr(Ts)，

(8)

(9)

由于钢轨单位长度电阻参数受地理参数影响较小，计算时取沿线环境温度即可。将式(9)代入式(1)得到考虑温度变化的单位长度的牵引网等效阻抗

Zgeo=(RC_20[1+αl(Ts-20)]+jXC)-

(10)

式中：RC_20、RT_20分别为单位长度接触线、单位长度钢轨在20 ℃下的电阻值；XC、XT分别为单位长度接触线、钢轨的电抗。

牵引网供电区段内各节点的等效阻抗

Zij=Zgeolij.

(11)

式中：lij为节点i至节点j的距离，单位 km；Zij为节点i、j之间的等效阻抗，单位 Ω。

由于铁路列车运行图相对固定，可将某供电区段一天内的工况可分为重载、轻载及空载。分别对供电臂不同工况下的负荷曲线进行分析，取其特征值作为该工况下计算牵引网输电导线电阻温度参数的依据。伴随着电气化铁路供电制式的改革(如同相供电等新型供电方式)，最显著的变化就是供电臂的辐射距离大幅增加，其应用场景多集中于地理气候条件较为复杂(实际气象参数取值与导线电气参数计算参考值有显著不同)的区段，如川藏线和兰新线。因此，在电气化铁路潮流计算过程中考虑牵引网架设沿线的地理气象参数对导线阻值的影响是十分必要的。

1.3 电热耦合影响下的线性潮流约束

基于支路潮流模型的最优潮流一般模型如下[9-10]：

(12)

由于式(12)中含有非线性部分，在使用商业软件求解时，需要对其进行线性转换，即对式(12)中电流幅值和电压幅值的平方进行变量替换，然后对最后一个约束进行二阶锥松弛，转换后的约束如下：

(13)

进一步将式(13)中的第1个和第5个约束中节点ij之间的电阻参数替换为式(14)所示的部分，在进行牵引网潮流最优约束中考虑输电导线电阻参数受其温度影响的因素，即：

(14)

式中r()、i()分别为取实部、虚部的函数。式(13)和(14)构成了松弛后的最优潮流基本模型。

2 储能主动参与的牵引网压波动抑制模型

2.1 储能主动参与的机车拓扑结构

车载储能系统(energy storage system，ESS)接入牵引供电系统的整体结构如图2所示。图中：IA，IB，IC为外网的三相电流；Iα、Iβ和Uα、Uβ分别为经过变换得到的牵引变压器α、β相的电流和电压；PL为机车牵引、制动功率；PESS为机车储能充放电功率。其中ESS主要由储能单元、储能变流器及双向DC/DC变换器构成。ESS通过双向变流器并联于电力机车主变二次侧，实现电量的余缺调剂，同时利用储能储存的有功，通过控制车载储能变流器实现供电区间再生制动、光伏等多源接入能量的优化利用和牵引网侧网压波动抑制[16-20]。

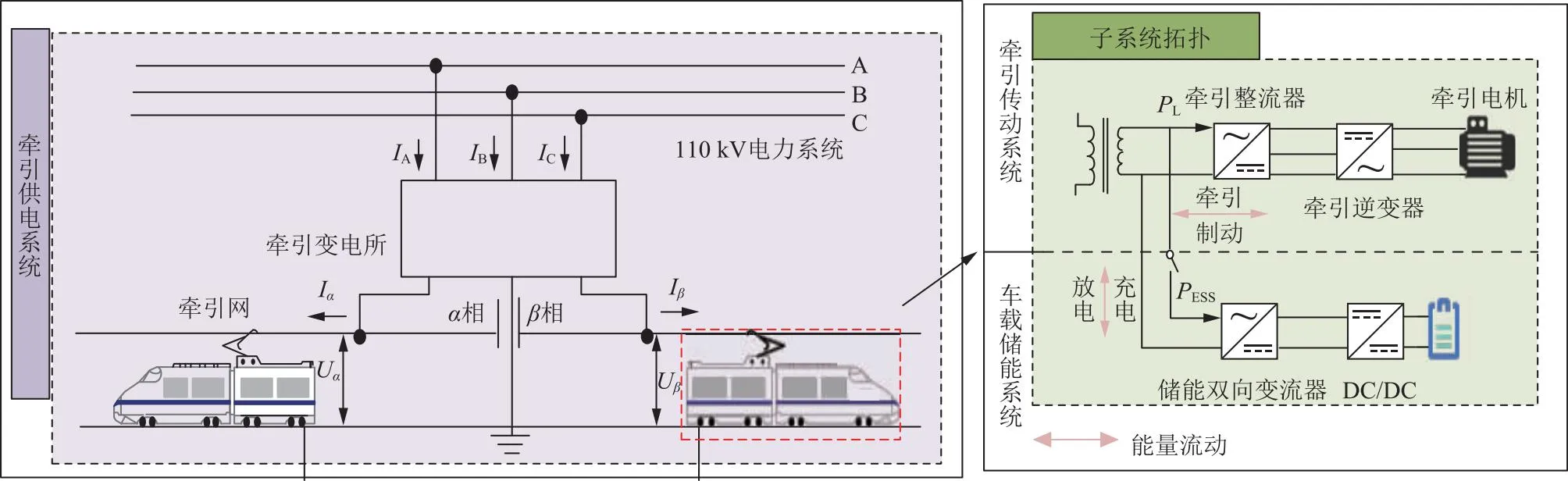
图2 车载储能系统拓扑Fig.2 Topology diagram of on-board energy storage system

2.2 目标函数

牵引网压协调优化控制的目标函数为机车端牵引网压偏差ΔU最小，见式(15)。该目标函数的目的是使机车端网压保持在满意的水平。作为检验系统安全性和电能质量的重要指标之一，目标函数可表示为

(15)

式中：T为计算周期；U0为牵引变压器低压侧出线等效电压。

2.3 约束条件

a) 电功率约束为

(16)

b) ESS运行约束包括充放电功率约束和荷电状态约束，为：

(17)

由式(17)可见储能有3种工作状态：充电、放电和空闲状态。在空闲状态下，储能系统不工作，能量水平也不改变(例如机车处于滑行模式时)；在充电状态下，储能充电；在放电状态下，储能系统能量水平随着其向供应负载释放能量而降低。储能系统每个状态的存储/释放能量可由式(17)的第6式计算。此外，当列车完成供电区间的运行时，ESS被控制为以额定功率吸收电网的能量，直到其达到SOC的初始值，为之后进入的供电区段抬升网压做准备。SOC被限定在一定区间是为了防止电池过充或过放，延长使用寿命。

3 算例分析

3.1 仿真描述

本文基于图2的拓扑，以国内某采用单线直供的供电区段为例对机车网压波动抑制过程进行分析。采用的详细电气仿真参数和采用的单元储能设备的参数见附表A。仿真工况下其负荷与机车距离牵引变电所的距离分布如图3所示，采样间隔为1 km，一个供电区间长度24 km，并考虑了机车运行沿线的地理气象参数对输电导线电阻温度的影响。可以应用相同策略对其他供电区域对机车端网压进行优化。该优化问题是一个混合整数线性规划问题，本文在MATLAB中调用CPLEX和YALMIP工具箱对优化问题进行求解。为减少仿真计算运行时长，简化模型，突出所提策略对机车端网压波动抑制的有效性，提出以下3个假设：

图3 牵引负荷随牵引距离分布Fig.3 Distribution of traction load with traction distance

a)假设机车以恒速在供电区段内运行，运行速度为96 km/h，通过该区段的时间为0.25 h，因此，机车SOC与时间分辨率Δt的耦合关系中，Δt取值为0.25 h；

b)假设机车的功率因数为1，暂不考虑机车的无功功率；

c)假设在计算输电导线受温度影响的阻值时，取牵引负荷分布的有效值的平均值作为式(14)中I的取值。

3.2 仿真场景

如图3所示，机车在4～12 km区段内牵引功率为负值，机车在制动工况下运行，其余区段处于牵引工况。

为验证本文所提方法的有效性和科学性，比较不同场景下的机车端网压波动抑制的效果，设计如下场景。

场景一：基于给定的机车负荷分布分别对是否考虑牵引网沿线地理气候参数对潮流计算的影响的2种情形计算单车下机车端网压。

在考虑牵引网沿线地理气候参数时，参考文献[21]设置极端寒冷条件下的潮流计算作为情景1(本文选取环境温度为-40 ℃，风速为18 m/s，海拔高度为10 m)和极端炎热条件下的潮流计算作为情景2(取环境温度为50 ℃，风速为0，海拔高度为4 000 m)，其他地理气候参数详见附录A1。将未考虑牵引网沿线地理气候参数的传统牵引潮流计算作为情景3。对这3种典型情景进行分析比较，以揭示机车端网压在不同地理气候参数下随机车牵引距离的分布。

图4展示了3种情景下的机车端网压随机车牵引距离分布的计算结果。

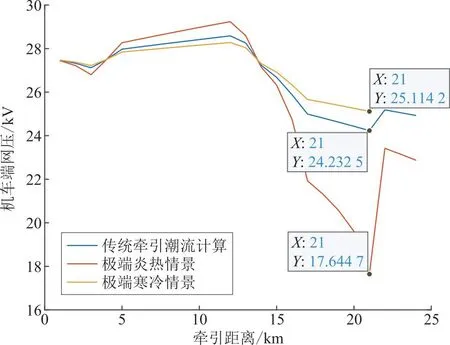
图4 3种典型情景下机车端网压随牵引距离分布Fig.4 Distribution of locomotive end network voltage with traction distance under three typical scenarios

由图4可以看出：牵引网网压在10 km以后出现大幅度快速的下降，主要是因为极端炎热情景下，环境温度高、风速低和海拔高度高等地理气候条件不利于输电导线散热，引起其运行温度升高；根据式(4)，输电导线的电阻阻值与输电导线运行温度呈正相关，其电阻阻值随温度升高而增大，同时叠加列车在10～20 km处于大功率牵引工况的影响，致使网压在10 km以后大幅度快速下降。以均方误差定义误差比例，得到情景1和情景2相对于情景3的均方误差分别为4.97%和0.21%，情景1相对于情景3的均方误差偏差较大，在情景1中，当机车运行至21 km时，机车端网压跌落至17.64 kV，超出了机车端网压允许范围，会造成机车牵引封锁。在情景3中，当机车运行至21 km时，机车端网压还在允许范围内。因此，牵引网沿线的地理气候参数，特别是环境温度、风速和海拔高度对机车端网压计算结果影响显著，调度中心在进行调度工作时有必要考虑牵引网沿线的地理气候参数。

场景二：考虑地理气候参数对输电导线电阻值影响的机车车载储能框架内的网压波动抑制过程。

使用本文所提策略与不使用该策略的牵引网极端炎热情景下网压对比如图5所示，图6所示是储能出力与网上取/给流的叠状图，储能出力在横坐标上方是储能放电状态，在横坐标下方是储能充电状态，出力为0时，意味着储能系统不工作。储能系统在机车端网压较高时，可吸收机车产生的制动能量，降低网压，避免超过牵引变流器的电压允许工作范围；在机车端网压较低时，可以通过给机车给流的方式，减小机车对牵引网的取流，使得牵引网压抬升至允许工作范围内。

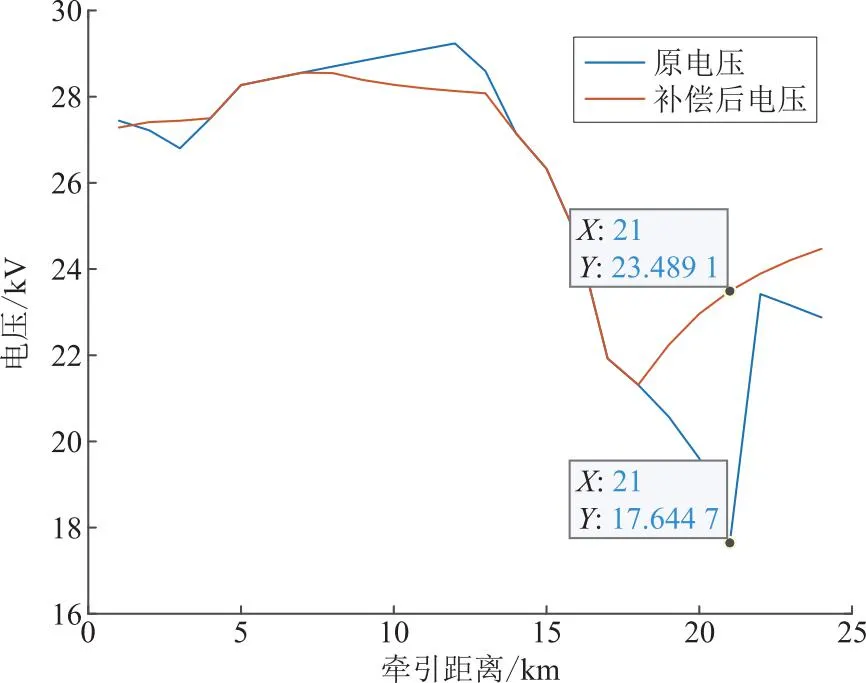
图5 极端炎热情景下采用本文所提策略与不使用该策略的机车端网压随机车牵引距离分布对比Fig.5 Comparison of locomotive terminal voltag e using the strategy proposed in this article and not using this strategy in extreme hot scenarios

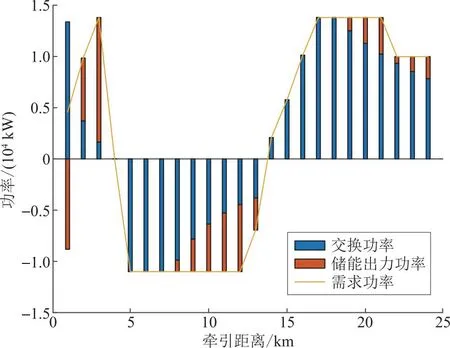
图6 极端炎热情景下储能出力与网上取/给流的叠状图Fig.6 Stacked diagram of energy storage output and traction network inflow/outflow under extreme hot conditions

结合图5和图6可以发现：由于本文所提策略的储能容量是一定的，机车储能系统在制动工况下(牵引距离6～9 km)，对机车制动功率进行吸收的同时抑制网压抬升并为储能后续动作提供能量。机车储能系统运行至21 km时放电，减少牵引网的负荷功率，并将机车网压由17.64 kV抬升至23.49 kV，确保牵引供电臂供电范围内机车网压工作在正常范围内。可见，在该极端情况下，所提策略可使机车避免牵引封锁，可靠稳定运行。

4 结论

本文基于车载超级电容电力机车框架和电热耦合理论，提出了计及线路电阻随温度变化影响的牵引网最优潮流约束的一种网压波动抑制策略。主要结论如下：

a)由于牵引网架设沿线的地理气象参数不同，机车端网压的计算结果也不同，在极端炎热情景下，计算网压与真实值偏差较大，因此在最优潮流约束中，有必要考虑地理气象参数对输电导线温度的影响；

b)本文所提策略可在有限的储能容量下更加有效地降低牵引网机车端网压偏差，在供电区段内可避免机车端网压超过或低于牵引变流器允许网压范围，避免牵引封锁，提高了机车运行的可靠性。