复合支柱绝缘子在长期载荷下的损伤识别方法

夏祥泰，曹枚根，张若愚

(1 北方工业大学 土木工程学院，北京 100144；2 上海大学 力学与工程科学学院，上海 200444)

随着特高压电网的迅速发展，对于变电站电气设备机械性能等方面的要求越来越高[1-3]。传统的瓷质材料电气设备由于材料自身脆性的原因，极易发生脆性损伤或断裂，相对而言，复合材料具有刚度大、强度高、韧性及抗疲劳性能好的优点[4]。复合材料电气设备在国外变电站的运用开始于20世纪70年代，国内在2000年左右也开始在各个变电站中使用复合绝缘子材料。现阶段，随着我国交直流输变电工程的快速发展，国内的多所变电站、换流站电气设备开始实现全面的复合化[5]。

然而随着变电站内复合电气设备种类越来越多，且投运时间越来越长，在力学性能方面的问题逐渐凸显出来。复合电气设备较容易受到环境中荷载的影响而产生微小损伤，尤其是在法兰节点位置，随着这些微小损伤的不断累积，就会对结构的安全产生威胁(如图1所示)，进而造成直接或者间接的经济损失。因此，对于复合电气设备进行不同服役阶段的损伤检测识别是非常有必要的。

图1 支柱类电气设备法兰节点损伤Fig.1 Damage to flange nodes of strut type electrical equipment

对于结构的损伤识别，现阶段较为常用的方法是通过结构动力特性的改变来进行判断[6-8]，其分析参数主要是包括固有频率、振型等。作为结构的2个重要固有参数，频率和振型当然可以来判断结构是否出现了损伤，但实际上，结构某一部位发生损伤破坏，对于结构的整体影响并不是很大，随着损伤程度的加深，结构频率和振型的改变是极其微小的，很难通过它们较好地判断结构的损伤情况。

于是通过大量学者的不断研究，提出了不同的损伤指标用于对结构进行损伤识别[9-11]。唐启智[12]等对于传统识别方法难以预测结果可靠性的问题，找到了一种基于自回归和高斯过程的损伤识别方法，能够有效地识别多损伤状态的情况，并能够实现损伤预警且结果较为准确。卢俊龙等[13]通过对古塔进行了原位动力特性测试，找到古塔的模态曲率幅值的突变规律，以此实现了对古塔结构的损伤定位，为塔类结构的损伤研究提供了重要参考。VB Dawari等[14]通过比较损坏和未损坏结构的动力特性来识别破坏，在模态曲率和模态柔性差的基础上，对混凝土梁中的蜂窝损伤进行识别和定位，表明这些方法对于损伤识别的有效性。吴多等[15]提出一种基于曲率模态曲线变化的损伤识别方法，采用多项式和神经网络技术，以曲率模态的参数指标为基础，对桥梁损伤前后的曲率模态曲线变化进行研究，验证了该识别方法的有效性。Yang等[16]为了深入了解结构的特征，提出一种利用结构柔性变化的特征参数分解的方法，用解耦的方式处理损伤识别问题，确定受损元素数量，开发了定位和量化算法。通过曲率模态的方法来进行结构损伤识别的技术已经越来越成熟，也被用于各行各业的工程领域当中。

鉴于变电站内复合电气设备的重要性、普及性以及在长期环境荷载作用下的易损性，以变电站内的复合支柱绝缘子为研究对象，采用曲率模态差以及小波变换的方法对其进行损伤识别及损伤程度的判断。首先通过对200 kV复合支柱绝缘子进行现场动力特性测试，求出其在不同损伤情况下的固有频率；随后通过数值模拟的方法得出各个损伤工况下的曲率模态差值，并对曲率模态差值进行小波变换；最后通过最小二乘法拟合出该绝缘子的多项式损伤曲线，进而验证以上方法对于绝缘子损伤识别的有效性。

1 曲率模态差及小波变换的损伤识别方法

1.1 曲率模态差基本原理

曲率模态代表弯曲振动结构的典型动态特性，其振型是承弯结构的中性面的特征变形，可以用来反映结构局部特性的变化。可以通过模态振型获得。

截面x处的曲率

(1)

式中：R(x)为曲率半径；M(x)、K(x)分别为截面x处的弯矩、抗弯刚度。由式(1)能够知道结构一旦发生了损伤破坏，那么对应位置处的抗弯刚度随之下降，进而曲率就会变大，曲率模态值随之变化。故可以利用曲率模态的方法对结构进行损伤识别诊断。

通常用中心差分的方法来计算曲率模态，假设结构被离散成多个单元[17]，其具体表达式为

(2)

式中：φ″i(j)为结构第i阶模态在j节点处的曲率模态；φi(j)为结构第i阶模态在j节点处的振型；lj-1，j为j-1节点到j节点的距离，lj，j+1为j节点到j+1节点的距离。

对于边界情况，当j=1时，

(3)

当j=m时，其中m表示最后一个节点，

(4)

以上为各阶曲率模态的求解方法，为了能够更好地对损伤破坏进行识别分析，采用曲率模态差变化的方法更加准确地识别出损伤位置。曲率模态差

Δφi(j)=φ″id(j)-φ″iu(j).

(5)

式中：Δφi(j)为第i阶模态在j节点处的曲率模态差；φ″id(j)为损伤情况第i阶模态在j节点处的曲率模态；φ″iu(j)为无损情况第i阶模态在j节点处的曲率模态。

1.2 小波变换基本原理

小波变换是一种时域频域的局部化精细分析方法，能够对输入的信号进行多尺度的分析，也是损伤检测的一种新途径。

小波变换的2个重要的参数分别是尺度因子a和平移因子b(a和b均为实数)[18]。设函数ψ(t)∈L2(R)，其中R为实数集，L2(R)为平方可积的实数空间，则ψ(t)经过缩放和平移后，会产生小波函数族

(6)

对于任意信号x(t)，其连续小波变换可表示为

(7)

式(7)是一个与a和b相关的函数(其中ψ*表示ψ的共轭)，反映了x(t)的变化速度情况。当尺度取得较小时，小波Wx(a，b)沿着t轴收缩，通过小波变换分析可以得到信号局部的信息；反之尺度取得较大时，小波沿着t轴延伸，通过小波变换可以得到信号的全局信息。

结构的损伤通常很微小且难以发现，利用小波变换能够将微小的损伤破坏信号放大，将不明显的信息变得更加易于观察，通过确定信号中存在奇异位置，可以判断结构的损伤位置。

2 不同损伤工况下绝缘子现场动力特性测试

2.1 测试对象

本次研究的对象是单节200 kV支柱绝缘子，其尺寸为外径217 mm，内径181 mm，高为2 400 mm。下、上部法兰分别定义为A、B法兰，安装图及其实物图如图2所示。其中令水平向右为X向，竖直方向为Y向。

图2 绝缘子安装图及其实物Fig.2 Insulator installation and physical drawings

2.2 测试过程

本次动力特性测试的输入荷载为电机振动荷载，如图2(b)所示，将电机置于B法兰上顶板，电机的激振频率为25 rad/s，则1 h可以作用9万次。将加速度传感器布置在绝缘子的中部，并对采集到的信号进行分析处理得到绝缘子振动特性。实测时的采样时长为25 s，采样频率设置为500 Hz。使用传感器数据采集处理软件来采集加速度数据。

首先需要对裸绝缘子进行动力特性测试，通过力锤敲击的方式，在顶部法兰自由端位置进行敲击，敲击次数共为3次，方向为X向。由于绝缘子结构以及底板为对称结构，故在X向和Y向的振型和频率相同。之后对敲击的绝缘子自由衰减曲线进行傅里叶变换得到其固有频率。其加速度傅里叶幅值谱如图3所示。

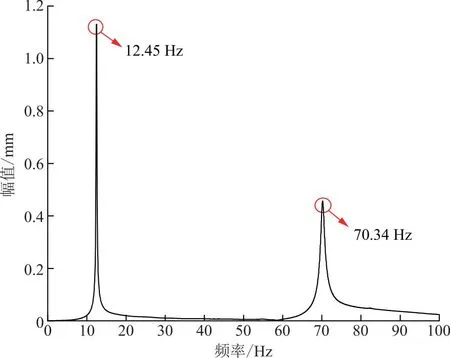
图3 绝缘子加速度傅里叶幅值谱Fig.3 Insulator acceleration Fourier amplitude spectrum

由图3可知：绝缘子及其底板的第一阶频率为12.45 Hz，第二阶频率为70.34 Hz。

随后对绝缘子进行不同工况下的动力特性测试，测试时间为7 d，每天进行时长为10 h的电机激励，总时长为70 h。设置电机不同的作用时间为不同的工况，分别为10、20、30、40、50、60、70 h的电机激励，在上述不同工况下，关掉电机，通过绝缘子的自由衰减获得其加速度衰减曲线，然后经过傅里叶变换得到不同损伤情况下的结构固有频率。

2.3 测试结果对比

由无损伤工况以及不同作用时间工况下的动力特性测试可以得到绝缘子固有频率的变化。提取它们前两阶频率，如图4所示。

图4 不同时间下绝缘子前两阶频率Fig.4 Frequency of the first two orders of insulator at different time

由图4可知，无论是一阶或者是二阶频率，在绝缘子受到损伤后，都存在不同程度的降低，损伤越严重，自振频率下降越多。自振频率的改变确实反映了损伤的发生。但是由图4也可以看出，在无损情况下和70 h电机激励的情况下，其频率变化不大，所以仅仅通过频率的变化很难定位出损伤位置。

3 绝缘子损伤识别分析

3.1 有限元模型的建立

以2.1节的安装图和实物图为原型来建模，由图1可知，200 kV单节绝缘子由一节套管和两边的法兰组成。为模拟真实测试情况，在绝缘子的底部将十字型肋板也建立出来，绝缘子伞裙无结构功能，建模时可以对直径略微调整。其材料参数见表1。

表1 绝缘子材料参数Tab.1 Insulator material parameters

采用分析软件Ansys来建立绝缘子的有限元模型。整个模型均采用Beam188单元来进行模拟，其中，在套管与法兰的连接段需要用等效梁单元来进行模拟。本次的研究对象为复合材料套管，实际情况中连接段的弯曲刚度要小于复合套管本身的弯曲刚度，约为复合套管的1/3～1/4[19]，本文连接段的刚度取复合套管的1/3.5。对等效梁部分进行网格加密处理，绝缘子的有限元模型如图5所示。

图5 绝缘子的有限元模型Fig.5 Insulator finite element model

3.2 动力特性分析及损伤工况模拟

对上述有限元模型进行动力特性分析，可以得到各阶频率，其前三阶频率与实测频率的对比见表2。

表2 绝缘子前三阶自振频率Tab.2 Insulator first three orders of self-oscillation frequency

由表2可知：绝缘子的前三阶自振频率的实测值与理论值相对误差较小，可以认为该有限元模型较好地模拟了绝缘子的实际结构。

支柱绝缘子的应力集中部位主要是法兰位置，也是首先产生损伤破坏的部位，即图5所示A、B法兰处，A法兰和B法兰与套管的连接处对应的单元分别为10号单元和41号单元，主要损伤工况见表3。

随着经济体制改革和经济全球化进程的加快，现代工程项目建设呈现出投资主体多元化、投资决策分权化、工程发包方式多样化、工程建设承包市场国际化以及项目管理复杂化的发展态势。因此，工程建设领域对具有合理知识结构、较高业务素质和较强实践技能，胜任工程建设全过程造价管理专业人才的需求量越来越大。应用型本科院校的人才培养能否把专业知识和技能熟练地应用在相关实践领域，成为衡量高等教育成果的重要指标。青岛工学院近几年围绕该教育理念不断探索和改革，旨在推动应用型人才培养和应用技术创新，建设高水平应用型技术大学。

表3 绝缘子主要损伤工况设计Tab.3 Design of major insulator damage conditions

表3为2种损伤类型下的损伤工况，然后分别通过曲率模态差值分析以及小波变换的方法对其进行损伤识别研究。

3.3 曲率模态差损伤识别

3.3.1 单一位置损伤识别

模态振型对损伤的不敏感性，故通过改进模态振型信号，用曲率模态差来进行损伤的识别。

首先是工况1—4对应的情况，将A法兰与套管的连接处，即10号单元，设置为损伤单元。结构损伤导致截面刚度的降低[20]，刚度变化为弹性模量和惯性矩引起的，可以通过改变弹性模量的方法来控制截面刚度的变化，进而模拟不同的损伤程度。分别对损伤程度30%、50%、70%、90%的工况进行模拟。

由动力特性分析可以得出各节点的振型位移，然后由1.1节的相关公式可以计算得出相邻各节点的曲率模态。则在单处损伤的情况下，曲率模态差变化曲线如图6所示。

图6 单损伤一阶曲率模态差Fig.6 The first order modal curvature difference of single damage

3.3.2 双处位置损伤识别

为了验证曲率模态差对于小损伤以及其他位置损伤的敏感性，再一次模拟损伤工况5—8，即双处位置的损伤识别，在双处损伤的情况下，曲率模态差变化曲线如图7所示。

图7 双损伤一阶曲率模态差Fig.7 The first order modal curvature difference of double damage

由图7可以知道，在损伤情况为2处时，也可以精准地判断出损伤位置，两处位置的突变都非常明显，只不过曲率模态的正负发生了变化，且底部的损伤突变要大于顶部损伤。在2处损伤的周围曲线也存在微小的凸起，与单处损伤情况相同，不会影响到损伤位置的识别。

3.4 小波变换损伤识别

小波变换不同于傅里叶变换，在进行小波变换之前需要确定好小波基以及分析尺度，小波基和分析尺度选取的不同也会导致分析结果的改变。

用于本次研究的小波变换是用来识别结构损伤，故本次选用适用的db2小波作为小波变换的小波基。

分析尺度为小波变换的尺度函数，分析尺度选取的越小，那么损伤位置的局部特征也就越为明显[21]，但是若是分析尺度过小，小波变换结果为原始信号的整体变化，会导致信号的细节变化不易看出，故需要将分析尺度选择在一个合理的区间，本次研究统一选取的分析尺度为5。

3.4.1 单一位置损伤识别

对工况1—4的曲率模态差值进行小波变换，可以得到单一位置损伤下小波系数随节点的变化曲线，如图8所示。

图8 单损伤小波变换计算结果Fig.8 Wavelet transform calculation results of single damage

由图8可知，小波系数在10号单元附近发生了突变，准确地识别出了损伤的位置，且相对于曲率模态差值的方法，小波系数在未受损的位置几乎是没有突变的，其识别效果更具优越性。另外，与曲率模态差值方法相同，在突变的位置，无论是正负，损伤程度越大，其突变效果越明显。

3.4.2 双处位置损伤识别

为了验证小波分析对于其他位置损伤是否同样具有敏感性，对工况5—8的曲率模态差值进行小波分析。在双处损伤的情况下，其小波系数随节点的变化曲线如图9所示。

图9 双损伤小波变换计算结果Fig.9 Wavelet transform calculation results of double damage

由图9可知：对于双处损伤的情况，小波变换的方法仍然适用，在损伤单元位置附近，曲线发生了大的突变，且在其余无损节点处几乎没有任何的凸起。

由此可知，曲率模态差值的方法可以用来进行绝缘子损伤识别的分析，在无损位置会有小的变化，但并不影响损伤位置的判断；小波变换与之相比，在无损位置几乎没有变化，更具优越性。

4 绝缘子损伤程度识别

在第3章中，已经计算出了10号单元在不同损伤工况下的曲率模态差，故以曲率模态差作为评价损伤程度的指标。由于4个工况样本太少，故增加损伤程度5%、10%、20%、40%、60%、80%这6种工况，分别计算出10号单元在各工况下的曲率模态差，10号单元各个损伤程度对应曲率模态差见表4。

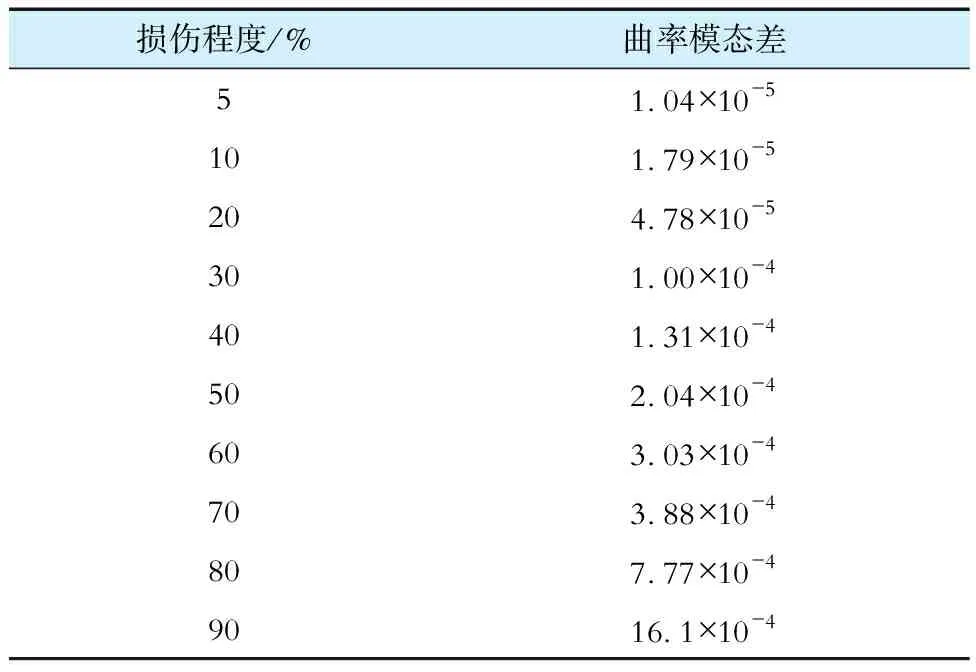
表4 不同损伤程度对应的曲率模态差值Tab.4 Differences in modal curvature corresponding to different damage levels

将表4中的数据以散点图的方式绘出，并通过最小二乘法拟合这些点，建立出曲率模态差值随损伤程度变化而变化的规律，其拟合多项式为

y=3×10-12x5-5×10-10x4+3×10-8x3- 8×10-7x2+10-5x-3×10-5.

(8)

为了提高拟合度r，多项式算到了第五次幂，此时的r为0.999 2，拟合情况已经较为精确。该多项式的曲线如图10所示。

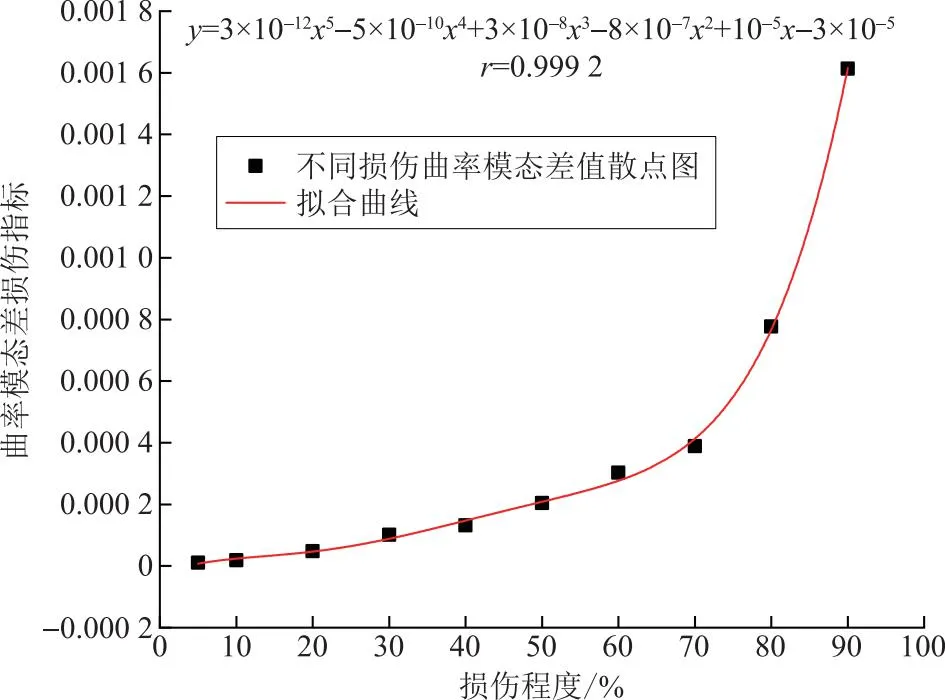
图10 损伤程度与损伤指标的拟合曲线Fig.10 Fitting curves of damage levels and damage indicators

为了验证该损伤曲线的准确性，令10号单元损伤程度为65%，此时有限元模拟曲率模态差值为3.59×10-4，将x=65代入上述多项式中，求得曲率模态差值为3.52×10-4，与模拟结果误差为1.94%。该结果表明，以曲率模态差值作为损伤指标拟合的多项式曲线，能够较为准确地识别出绝缘子的损伤程度。

5 结论

为了研究变电站复合电气设备的损伤识别方法，本文以变电站内复合支柱绝缘子作为研究对象，对其进行了现场的动力特性测试，提取不同损伤程度下的自振频率进行对比。然后用曲率模态差和小波变换的方法，对其进行不同工况下的损伤识别。得出的主要结论如下：

a)对复合支柱绝缘子进行不同损伤程度现场动力特性测试，前两阶频率为12.45 Hz和70.34 Hz。随着结构损伤加剧，频率逐渐下降，损伤越严重频率下降越多。但是损伤最严重时，前两阶频率仅下降为11.42 Hz和68.24 Hz，频率随着损伤程度的增大变化很小，不能够很好地进行损伤位置的识别。

b)由现场动力特性测试结果建立精确的有限元模型，通过曲率模态差值法和小波变换的方法对10、41号单元进行30%、50%、70%、90%损伤程度下的损伤识别，2种方法均可有效地对绝缘子进行损伤识别，且小波变换的方法更具优越性。

c)以曲率模态差作为损伤指标，增加损伤程度为5%、10%、20%、40%、60%、80%的损伤工况，基于最小二乘法来拟合出复合绝缘子的损伤程度曲线，拟合多项式的拟合度为0.999 2。然后对拟合曲线进行验证，证实了该拟合曲线对所研究绝缘子损伤程度判断的准确性。