基于RF-PSO 的塔吊事故可能发生阶段预测与分析＊

刘冬华 赵星 赵江平 杨震

（西安建筑科技大学资源工程学院，陕西西安 710055）

0 引言

随着城市化的不断发展，塔式起重机（简称塔吊）在高层建筑乃至超高层建筑的施工现场最为常见。塔吊在施工现场经历不同的阶段，包括安装、使用、攀爬和拆卸，在这些阶段的工作内容中，需要人、机、物、管、环境等方面的配合，无论任何环节发生问题，都可能引发事故［1］。因此，预测塔吊事故可能发生的阶段对预防塔吊事故发生具有重要意义。

近年来，随着机器学习的兴起，相比于传统的事故预测方法，机器学习算法在事故预测中表现的更加简单、快捷，可以处理复杂的非线性关系，且具有更高的预测精度。例如，LIN N［2］基于神经网络模型，考虑了人为因素、机械设备和环境因素3 个层面以预测高层建筑的塔吊风险。况宇琦［3］基于支持向量机建立了塔吊事故类型预测模型，同时比较了网格搜索法、粒子群算法、遗传算法3 种参数优化的方法。JIANG L 等［4］利用MI 改进RF 模型，在塔吊事故数据不完整的情况下预测塔吊事故，提供了塔吊事故影响因素的重要性等级，表明塔吊安全管理更应集中在作业现场。目前，许多机器学习算法被广泛应用于建筑事故预测。BP 神经网络的预测准确度较高，但其计算量非常大；决策树（DT）是一种常用的数据挖掘措施，但其容易产生过拟合；支持向量机（SVM）能够有效防止“维数灾难”，增强非线性数据的拟合能力［5］。在机器学习的众多算法中，RF 是近几年新出的一种机器学习模型，是集成学习思想下的产物，它的提出在运算量没有明显增大的前提条件下使得模型的预测精确度明显进步，最早是由BREIMAN L［6］开发的RF 模型，是一种用于分类和回归的集成学习方法。RF的预测精确度受参数设置的影响很大，为了提高RF 模型的精确度，可以使用优化算法对其参数进行调整。目前，常用的参数优化算法包括网格搜寻（GS）、遗传算法（GA）、贝叶斯优化（BO）和蚁群优化算法（PSO）［5］。

本文基于HFACS 模型，从不安全行为、不安全行为的前提、不安全监管和组织影响4 个层面来构建塔吊事故致因框架，从塔吊不同作业阶段入手，采用卡方检验对影响因素进行量化，同时，利用RF 在预测精确度和解释能力方面的优势预测塔吊事故可能发生的阶段，此外，为了提高预测模型的精确度，采用PSO 对RF 进行参数调整，记为RF-PSO 预测模型。根据预测结果，可实施塔吊的事故预防措施。

1 塔吊事故案例数据分析与处理

1.1 数据收集

从国家应急管理部及地方应急管理局官方网站搜集整理344 份具有完整信息的塔吊事故调查报告。这344 起事故发生于2012 年至2022 年，造成390 人死亡、214 人受伤，经济损失高达50 000 万人民币。其中，一般起重伤害事故294 起（占85.47%），较大起重伤害事故49 起（占14.24%），重大起重伤害事故1起（占0.29%）。按塔吊不同作业阶段区分事故，在塔吊的安拆阶段发生事故149 起（占43.31%），吊装阶段发生事故161 起（占46.80%），攀爬阶段发生事故34 起（占9.88%）。

通过分析报告的内容，根据HFACS 模型［7］建立起重机操作风险目录，得到了影响塔吊安全的34 个因素，如表1 所示。

表1 塔吊事故影响因素

1.2 特征筛选

HFACS 模型包含了系统中组织管理-监管-作业人员的行为，定性地给出了影响因素之间的关系。但塔吊作业过程是一个复杂的动态过程，事故的发生原因有显性和隐性的区别，因此，需要利用定量的方法研究影响因素之间的关系。

根据HFACS模型各层次的特点，运用统计学中卡方检验对34 个塔吊事故影响因素进行量化分析。卡方检验是以Pearson卡方的统计量为基础，通过比较理论频数分布与观察频数的差距，由此推断p值的大小［8］。卡方检验的统计量如式（1）所示：

式中，r为列联表的行数；c为列联表的列数；fij0为观察频数；fije代表理论频数，其中×CT，RT代表总的行观察频数，CT代表总的列观察频数。

卡方检验是一种假设检验方法，它表示统计样本的实际观测值与理论推断值之间的偏离程度。当f0=fe时2=0；当f0与fe相差很大时2的值也很大，反之2的值则越小。

这里涉及的因变量是三分类变量，自变量是二分类。利用2×3 列联表的形式对卡方检验的数据进行统计，如表2 所示，其中，a、b、c、d、e、f分别代表各单元格对应的实际观测频数（一般情况下，1：发生；0：不发生；令安拆=2，吊装=3，攀爬=4）。

表2 2×3 列联

一般认为当p＜0.05 时，有较强的证据拒绝原假设H1，即塔吊不同作业阶段与事故影响因素之间的关联性较强；当p＜0.01 时，有极强的证据拒绝原假设H1，即塔吊不同作业阶段与事故影响因素之间的关联性极强。将p＜0.05 的结果统计如表3 所示。

表3 2 值统计结果

表3 2 值统计结果

影响因素images/BZ_65_724_1399_749_1426.png2 p O038.5210.014 O047.6100.022 O0821.5950.000 O0911.7620.003 US0111.6150.003 US0224.6890.000 US0412.0930.002 P0122.8130.000 P0220.5930.000 P0312.2420.002 P0417.3360.000 P0730.3430.000 P1030.3400.000 P1137.8330.000 UA0114.7680.001 UA0246.7360.000 UA0369.7330.000 UA0429.8040.000 UA0510.3550.006

对34 个事故影响因素进行检验，发现有19 个影响因素拒绝原假设，即有理由认为塔吊不同作业阶段与事故影响因素之间存在显著关联，在预测建模时应考虑将这些因素作为输入变量。

1.3 数据预处理

在搜集的334 起塔吊事故调查报告中，攀爬阶段发生事故仅占所有事故的9.88%，安拆和吊装阶段的事故数量明显高于攀爬阶段。样本数据不平衡现象十分严重，这种不平衡的数据可能会导致预测模型的不合理，降低其精确度。在这种情况下，采用SMOTE算法来解决数据不平衡的问题，该算法的核心是在最接近某个少数样本的k个样本之间插入n个人工合成的少数样本，从而增加少数样本的数量［9］。

利用SMOTE算法对样本进行扩充，通过多次实验确定最佳k值，不同k值下RF-PSO 模型的精确度及AUC 如图1 所示。可以看到，当k=2 时模型的表现最好，因此，在后文的预测中选择k=2 时的数据样本进行模型训练及预测。

图1 基于RF-PSO 的塔吊事故可能发生阶段预测模型的精确度及AUC 值

2 RF-PSO 预测模型的建立

2.1 随机森林（RF）

随机森林（RF）本质上就是一个包含多个决策树的分类器，构建随机森林，首先从原数据中采取有放回的抽样，构造出一个和原数据集数据量相同的子数据集，它控制决策树各不相同的方法就是控制最优的特征，使其随机选取［6］。图2 描述了RF 算法的原理。

图2 RF 算法原理

相关研究表明，影响RF预测性能的主要参数包括随机森林中决策树的个数（n-estimators）和最大特征数（max-feature），本文将主要针对这2 个参数对RF 模型进行优化改进［5］。

2.2 参数优化

参数优化能提高预测模型的精确度［10］。基于参考文献［5］的研究结果可以看出，对于RF 来说，PSO比常用的参数优化算法模型具有更好的效果。

PSO 是一种基于群智能的算法，与GA 相比，PSO 更关注种群中个体之间的交互。假设粒子的运动速度为V、位置为X，决策变量的维数为d，则第i个粒子的参数为：

式（3）—式（6）中，Pidt、Pgdt为t时刻个体与群体经历过的最佳位置；为惯性权重；r1、r2为［0，1］中的随机数；c1、c2为加速度常数；t为当前的迭代次数。其中，t和t+1 表示算法的连续2 次迭代。

用PSO 算法优化RF 参数的步骤如下：

①初始化粒子的初始速度与位置以及群体规模、最大迭代次数、加速度常数等参数。

②依据分类性能的评价函数，计算各个粒子的适应度值。

③将每个粒子当前位置的适应度值同其历史最佳位置Pidt的适应度值进行对比，如果更优，则用当前位置更新粒子最优位置，否则维持不变。

④将每个粒子当前位置的适应度值同群体最佳位置Pgdt的适应度值进行对比，如果更优，则用当前位置更新群体最优位置，否则维持不变。

⑤按照式（5）—式（6）更新粒子的速度和位置。

⑥判断是否满足寻优中止条件，如果满足则求出最优解，如果不满足则转至步骤②。

RF-PSO 预测模型的构建流程如图3 所示。

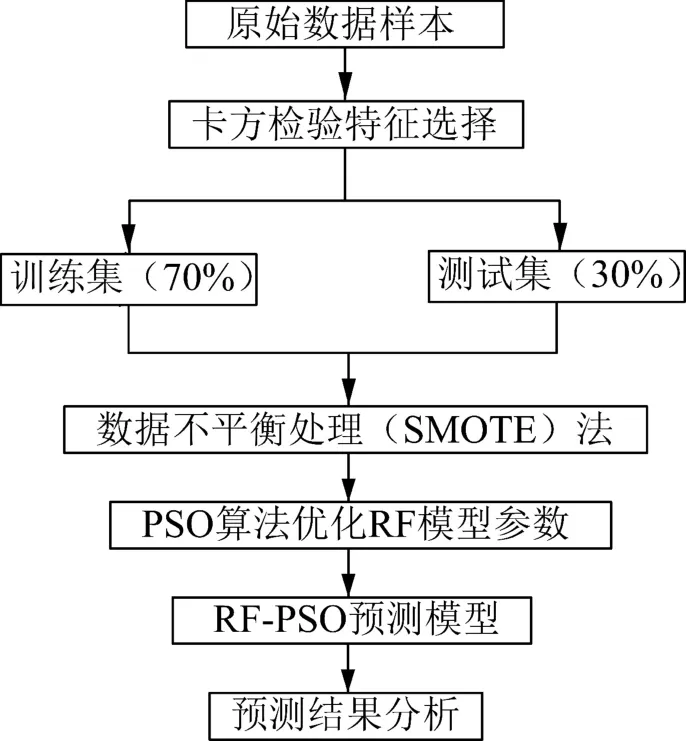
图3 基于RF-PSO 的塔吊事故可能发生阶段预测模型

2.3 模型评价

评价RF 模型效果可利用精确度（Precision）、召回率（Recall）和F1 分数（F-Score）3 个指标对模型预测性能进行评价［6］。其中，测试集中被正确分类的数量记为TP（True positive），被错误分类的数量记为FP（False positive），被正确分类为其他类型的数量记为TN（True negative），被错误分类为其他类型的数量记为FN（False negative）。则精确度、召回率及F1 分数可由式（7）—式（9）计算：

3 结果分析

3.1 模型比较

为了验证RF-PSO 模型在预测塔吊事故可能发生阶段的性能，将其与几种常用的预测模型进行比较，包括SVM、BP、RF 及RF-PSO。比较各预测模型的精确度、召回率、F1 分数及AUC，结果如表4 所示，可以看出RF-PSO 模型效果最好。

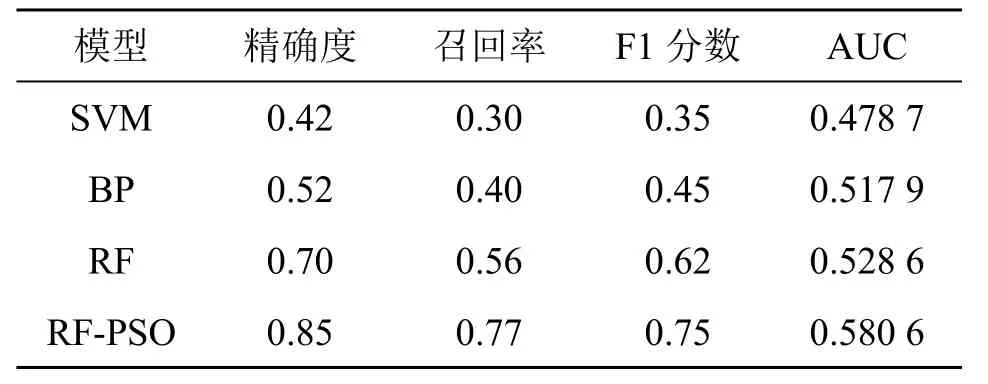
表4 模型比较

几种模型在预测塔吊事故可能发生阶段的预测性能如图4所示，可以看出RF-PSO的分类性能最好。

3.2 模型解释

RF 的一个重要优点是可以得到特征重要性排序，如图5所示。根据图5，安拆人员违规操作（UA03）、个人防护设备缺失（P07）和塔吊司机违规操作（UA01）的重要程度较高。根据分析塔吊事故，当UA03 发生时，即安拆作业人员错误操作，塔吊容易在安拆阶段发生事故。当P07 发生时，即作业人员在攀爬塔吊的过程中缺少防护措施，塔吊容易在攀爬阶段发生事故。当UA01 发生，即塔吊司机存在错误操作，塔吊在吊装阶段容易发生事故。

图5 特征重要性排序

实际上，在塔吊事故可能发生的阶段中，安拆阶段的作业程序十分复杂，需要专业和详细的操作规程来指导作业，这也是安拆阶段发生事故数量较多的原因之一。塔吊在吊装阶段需要塔吊司机、信号司索工等各类作业人员的密切配合。监管人员不仅要对作业人员进行资格审查，更应在日常作业阶段在作业现场进行安全监管。

除此之外，为了更好地解释预测模型，结合图5，根据RF-PSO 模型中的部分依赖图（Partial dependence）来研究输入变量对塔吊事故可能发生阶段的影响，如图6 所示。影响因素O03、US02、UA03 的发生概率越大，塔吊在安拆阶段发生事故的可能性越大。影响因素P11、UA01、UA02 的发生概率越大，塔吊在吊装阶段发生事故的可能性越大。影响因素P01、P03、P07 的发生概率越大，塔吊在攀爬阶段发生事故的可能性越大。

图6 塔吊事故关键影响因素的部分依赖关系

4 结论

（1）利用HFACS模型，从人的不安全行为、人的不安全行为的前提、不安全监管和组织影响4 个层面，着重分析了塔吊不同作业阶段的事故致因，总结得到34 个塔吊事故影响因素，同时利用卡方检验对其进行特征筛选和量化分析，得到19 个影响因素与塔吊不同作业阶段存在显著关联。

（2）提出了一种混合机器学习模型RF-PSO，利用SMOTE进行数据不平衡处理，并将其应用于塔吊事故可能发生阶段的预测分析，模型精确度高达85%。

（3）结果表明，影响因素塔吊安装不符合设计要求（O03）、缺乏沟通（P11）、个人防护设备缺失（P01）发生的概率越大，塔吊事故分别在安拆阶段、吊装阶段、攀爬阶段发生事故的可能性越大，针对不同作业阶段的塔吊需要采取不同的事故预防措施。