基于B型深孔测斜曲线的滑坡滑动面位置确定方法

陈 浩,吴红刚

(1. 兰州理工大学 土木工程学院,甘肃 兰州 730070; 2. 中铁西北科学研究院有限公司,甘肃 兰州 730070)

0 引言

边坡内部位移作为了解滑坡动态的重要数据,在各类滑坡变形研究的过程中一直备受重视[1]。尤其在滑坡变形监测中,位移作为最主要的参数,其变化特征是滑坡变形及运动特征的直观反映[2-4]。而其中,滑坡深部位移监测是滑坡变形监测的重要内容,能够对准确确定滑面位置、研究滑坡目前性状及其发展趋势以及整治工程设计提供重要的信息[5-7]。

围绕滑坡深部位移监测,研究学者从曲线变形特征、坡体受力特点、坡体结构等方面做了深入的研究和分析[8-10]。靳晓光[11]总结归纳了不同类型的滑坡深部位移监测成果,将滑坡深部累积位移曲线分为了“V”型、“B”型、“D”型、“r”型、复合型等几种,不同的曲线类型分别代表不同的坡体运动特征,并被不少研究学者广泛运用于实际滑坡中的滑面位置确定以及坡体稳定性分析上[12-15]。潘慧芳[16]结合变形曲线类型通过FLAC数值模拟的方法,分析了不同结构破坏类型下不同位置处的测点位移曲线特征与滑动面之间的关系。而目前,相关的研究主要集中在理论分析与实际变形曲线的对比分析上,鲜有测斜曲线监测数据与滑面位置辨识相结合的深入研究,通常是将测斜曲线突变点或位移最大点对应的深度作为滑动面的位置,这种滑面辨识方法虽然简单直接,但缺乏科学可靠的数学处理手段和数据挖掘方法,易受测斜仪上测点布置间隔及坐标观测尺度的影响,存在滑面位置定义不清晰、数值不确定的问题[17-20]。

为了能够有效地克服这些缺点,解决“B”型测斜曲线中存在的问题,提升深孔位移监测数据的利用程度。本研究基于“B”型曲线的变形特征,结合其滑动面处上下部土体的运动特点,建立相应的概化模型,考虑不同位置处的土体位移速率和加速度变化规律,进而提取加速度与滑动面位置之间的关系,从而构建一种可行的滑面位置计算方法,使滑动面位置的确定可计算化,为各类深孔测斜曲线的深入挖掘及滑坡防治工程设计提供参考和依据。

1 概化模型分析

1.1 曲线类型分析

根据深孔测斜曲线的形态特征,研究学者[14,21-22]将其分为了“V”型、“B”型、“D”型、“r”型、钟摆型和复合型6种。其中,能够表明滑坡滑动面迹象显著的深孔测斜曲线类型主要为“B”型、“D”型及“r”型3种[23]。

对于“B”型深孔测斜曲线(图1),滑坡“B”型变形特征是指滑坡有2个或2个以上明显的滑动面,但各滑块(体)的运动速率不一致,滑坡以其中一个滑面处的相对运动为主,滑坡整体处于蠕变-滑移阶段[11,24]。

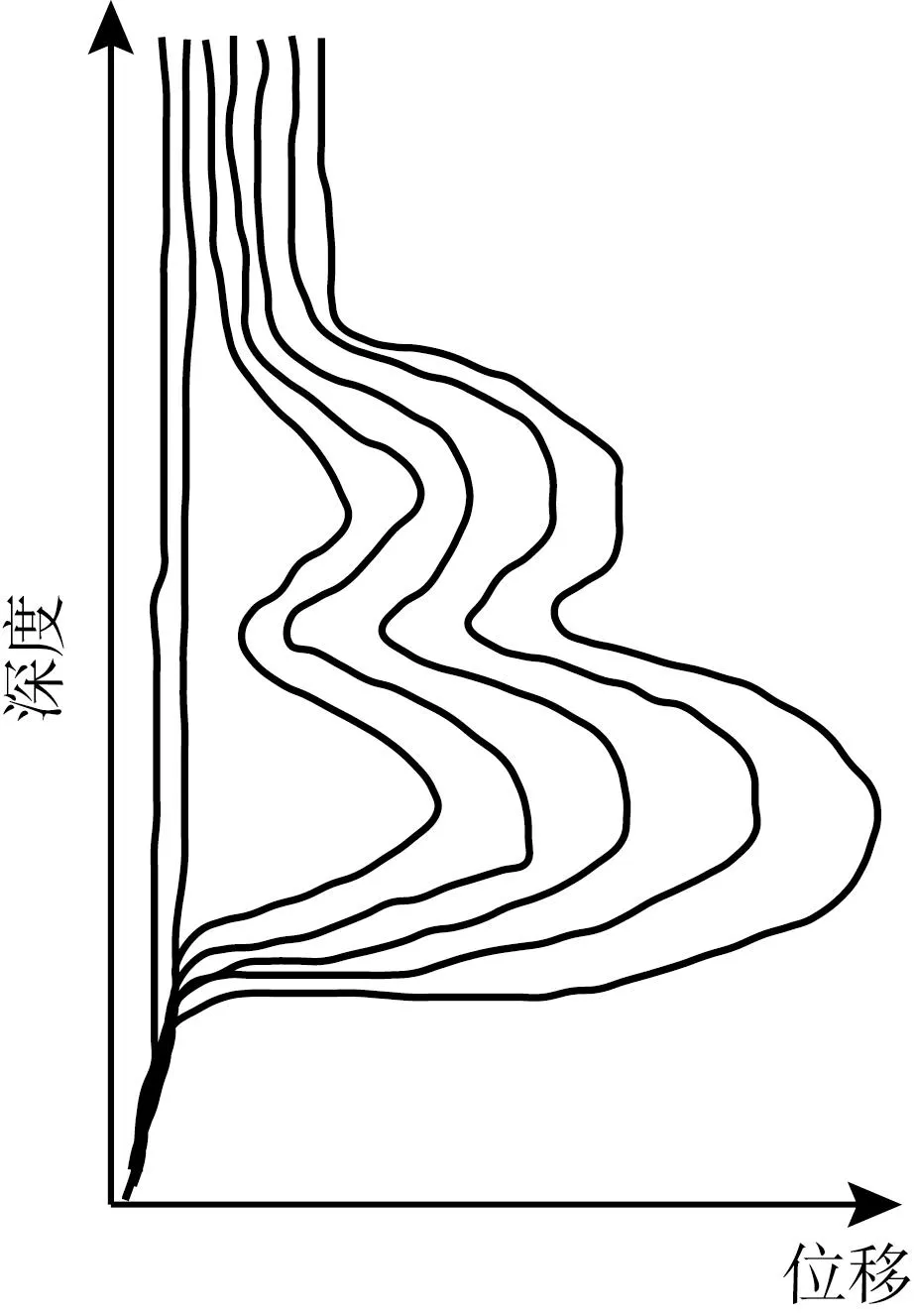
图1 “B”型测斜曲线Fig. 1 B-type inclinometer curves

此外,李迪等[25]根据各类变形曲线的特征、机理和存在的潜在不稳定因素,将深孔测斜曲线分为了四类,分别为稳定型变形曲线、滑动型变形曲线、坍塌型变形曲线和倾覆型变形曲线。依据这一分类方法,则“B”型测斜曲线属于坍塌型变形曲线,常发生在顺层滑坡中,以压剪变形为主,容易出现在松土带、软硬材料相间、断层、裂隙和裂缝处。

1.2 概化模型构建

由上述分析可知,具有“B”型曲线特征的滑坡,存在至少2个及2个以上的滑动面,且滑动面之间以相对运动为主。故在滑坡的运动变形过程中,受压力和剪力的共同作用,坡体沿深度方向产生剪压变形,而由于滑带附近土质软弱,该位置处的土体变形最大,且滑动面的存在使得上下部土体之间产生了明显的位移差。此外,随着时间的推移,滑带的发展变形对其上下部土体产生牵连作用,使得周围土体产生协同变形,而由于该类曲线的滑坡滑动面并未完全贯通仍处在变形滑移的阶段,则土体变形沿深度方向呈现近似鼓包凸起的形状,且凸起点的位置与滑动面的位置相对应。

与此同时,不同滑动面之间存在着相对运动,以滑动面的位移量作为辨识主滑面的关键依据,则主滑面的发展变形会带动与其相连的上下部土体共同运动进而产生挤压变形,且滑面之间的土体迁移运动进一步促进了相邻滑面的发展。因此,在多滑面的共同变形作用下,土体变形沿深度方向会呈现多鼓包凸起且近似“B”型的形状。

为了便于说明并体现滑坡各组成部分的运动特点,本文将滑坡体、滑动带及滑床分别称为滑动体、滑动区间和不动体,其概化模型如图2所示。

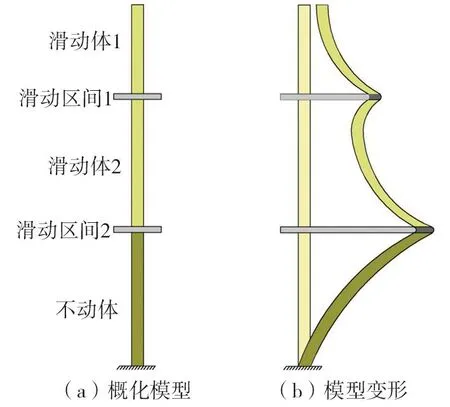
图2 概化模型Fig. 2 Generalized model

1.3 土体位移速率分析

1.3.1 区间位移速率分析

在实际的坡体运动过程中,不同深度处的土体因其所在位置、土体性质、滑动面发展程度等因素的差异而具有不同的位移速率。对于具有“B”型曲线特征的滑坡体而言,滑动区间所在位置是土体变形量最大且变形速率最快的区域,则与滑动区间相邻的一定范围内的土体在滑面变形作用下,相较于远离滑面位置处的土体具有更加显著的位移量和更快的变形速率。因此,以坡体鼓包凸起区间处的土体作为主要分析对象,则有助于提取位移速率沿深度方向的分布规律。

基于概化模型,将水平位移量最大的滑动面称为主滑面,反之,水平位移量较小的滑动面称为次滑面,分别对土体位移速率在不同滑动区间内的变化关系进行研究分析,如图3所示。

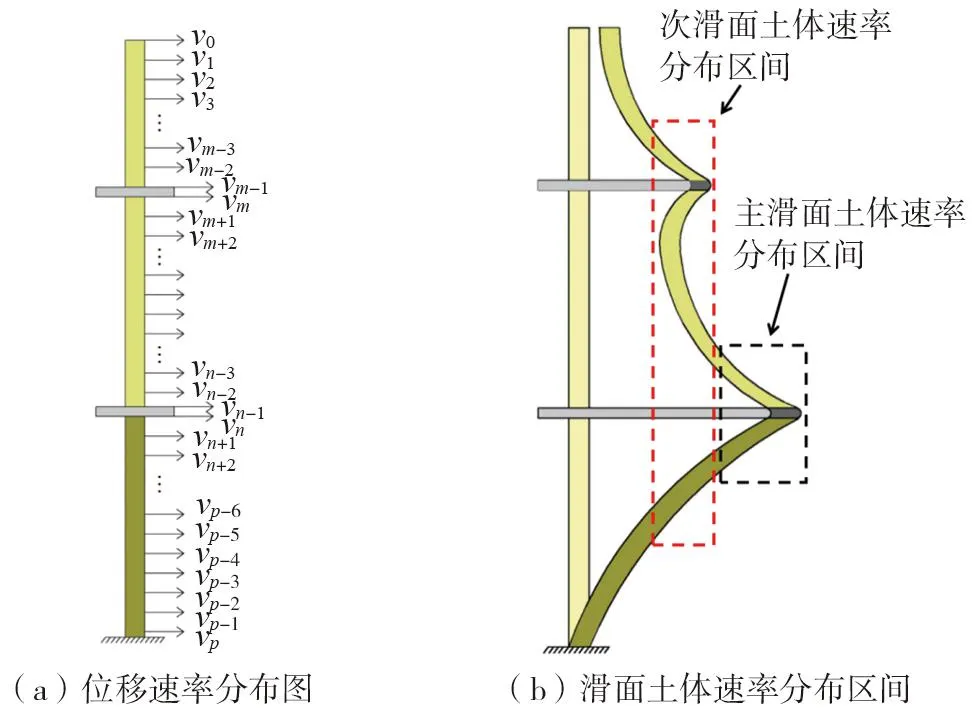
图3 概化模型位移速率Fig. 3 Displacement rate of generalized model

1)由图3(b)可知,主滑面所在的鼓包凸起区间是坡体沿深度方向水平位移最大峰值所在区域,由于主滑面的土体变形量大、发展程度深,则该区间内的土体位移速率会明显大于其余位置处的土体位移速率。其中,土体愈靠近滑动面其位移变形愈显著,使得以滑动面为中心的上下一定区间范围内的土体位移速率密集分布形成速率曲线簇,即图3(b)中主滑面土体速率分布区间对应的土体位移速率vn-3、vn-2、…、vn+2(图3(a))会形成速率值较大的速率曲线簇。

2)若排除主滑面土体速率分区间,则次滑面所在的鼓包凸起区间变成了坡体沿深度方向水平位移量最大的区域。同理,受滑动面运动产生的压剪作用,越靠近滑面位置处的土体变形量越大、变形速率也越大,则图3(b)中次滑面土体速率分布区间对应的土体位移速率vm-3、vm-2、…、vm+2(图3(a))将密集分布形成速率曲线簇。与此同时,概化模型下部不动体的弯曲变形与主滑面的凸起变形相连,则下部不动体部分区间内的土体变形量与次滑面速率分布区间内的土体变形量相等,由于土体变形时间相同且位移量相等,故2个区间内的土体位移速率一致,从而存在速率曲线相互重叠的情况。因此,相较于主滑面土体速率分布区间,次滑面土体速率分布区间更大,且沿深度方向向下延伸至不动体。

3)除去主、次滑面土体速率分布区间,则剩余位置处的土体变形量较小,位移速率趋近相同并明显小于主、次滑面分布区间内的土体速率,从而单独形成新的速率曲线簇。即v0、v1、v2、v3和vp-6、vp-5、...、vp-1、vp(图3(a))共同形成新的位移速率曲线簇。

1.3.2 位移速率曲线簇分析

通过上述分析,假设钻孔内测点的布置间隔一致,且钻孔深度足够大。以时间为横坐标速率值为纵坐标,则理想状态下土体位移速率沿深度方向的速率曲线分布特征如图4所示。

图4 位移速率曲线Fig. 4 Displacement rate curves

由图4可知,速率曲线明显分为3道曲线簇,分别对应主滑面、次滑面和非滑面3个分布区间(即图3(b)主、次滑面土体速率分布区间及剩余分布区间)。此外,曲线簇之间的速率差异使得彼此之间存在着一定的间隔区间,而这个特征能够作为划分土体滑动区间的重要依据。但是,由前面的分析可知,土体位移速率沿深度方向并不是成比例关系的线性变化,即位移速率的大小与土体深度并没有直接的关联,如次滑面速率曲线簇中既有滑动区间1内的土体位移速率曲线,同时也包含下部不动体部分深度范围内的土体位移速率曲线。因此,在土体速率曲线分簇特征的基础之上,如何进一步提取土体深度与位移速率之间的关系,是辨识滑面位置的重要内容。

研究择取曲线分簇特征显著的某一时期下的当日坡体不同深度处的位移速率值,以深度为横坐标、位移速率值为纵坐标绘制散点图,各个散点之间的水平间隔相同,则可以得到理想状态下位移速率-深度散点图,如图5所示。

由图5可知:

图5 土体位移速率散点图Fig. 5 Scatter plots of soil displacement rate

1)各滑面土体速率分布区间与其对应的滑面鼓包凸起深度区间相交的区域,速率散点密集分布形成散点簇,且明显游离于非滑面土体速率分布区间内的速率散点。本研究将这一特征称为滑动区间的速率游离特征。

2)速率散点的游离特征可以更加清晰地确定坡体鼓包凸起区域的深度区间,能够将各滑面鼓包凸起深度区间的分布范围由直观的定性判断变为具体的定量判断,且有利于滑面位置的准确辨识。

具有“B”型曲线特征的滑坡其土体变形具有连续性,当滑动区间处的土体变形量相对较小时,则不同的土体速率分布区间彼此之间的速率散点簇间隔相差较小,使得不同区间内的速率散点游离特征变得并不显著,导致各滑面所在滑动区间的深度范围不易区分。

1.4 土体加速度分析

通过前面的分析可知,位移速率散点能够较好地区分土体的滑动区间,并确定各滑动区间的深度范围。但是,受土体变形量及土体变形连续性的影响,位移速率散点的游离特征不一定显著。

相较于其余位置的土体,滑动区间内的土体具有更大的变形量和位移速率。而加速度作为描述物体速度变化快慢的物理量,将土体加速度作为不同位置处土体运动性能的衡量指标,相比于位移速率更能凸显区间内土体运动性能的差异。

若将图4中的位移速率-时间曲线转变为加速度-时间曲线,则两者的曲线分簇特征相似,且由于不同位置处土体彼此间的位移速率比例明显小于加速度比例,使得曲线簇之间的间隔区间更大。同理,择取曲线分簇特征显著的某一时期下的当日坡体不同深度处加速度值,以深度为横坐标、加速度值为纵坐标绘制散点图,可以得到理想状态下加速度-深度散点图,如图6所示。

由图6可知:

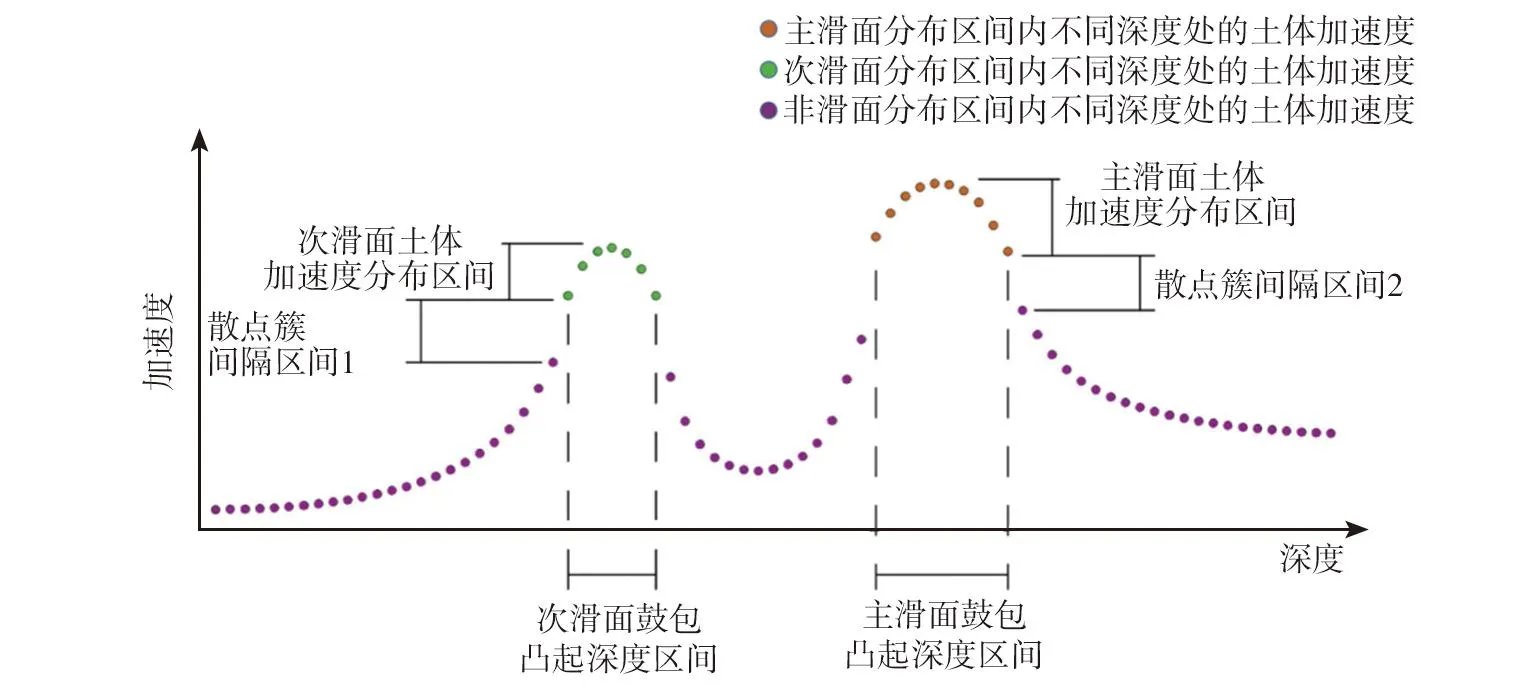
图6 土体位移加速度散点图Fig. 6 Scatter plots of soil displacement acceleration

1)各滑面土体加速度分布区间内的散点分布更加密集,且各区间内的加速度散点簇具有更加显著的游离特征。

2)不同的土体加速度分布区间彼此之间的散点簇间隔更大,即散点簇间隔区间1和区间2明显,相较于速率散点图能够更加直接准确地辨识坡体滑动区间及其对应的深度范围。

3)提取各滑面土体加速度分布区间内的散点数据,可以快速准确地缩小滑动面所在区间的分布范围,极大地降低无关数据对滑面位置辨识的干扰,并为滑面位置的确定提供关键依据。

因此,通过上述理论分析可知,对于具有“B”型曲线特征的滑坡可将土体加速度作为滑面位置辨识的重要指标。

2 实际运用分析

2.1 钻孔概况

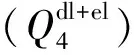
图7 滑坡实景图Fig. 7 Realistic view of landslide

基于上述理论分析,本文选取位于2号滑坡内的ZK2-5钻孔的实际监测数据进行分析验证,如图8所示,孔全深为32.5 m,数据采集深度为0.5～32.5 m,测点布置间隔为0.5 m,数据采集时间为2018年5月16日—2020年4月2日。由于采样时间间隔密集,为了便于展示曲线的变形特征,选取部分日期下的深孔位移绘制测斜曲线,结果如图9所示,可见曲线有典型的“B”型曲线特征。

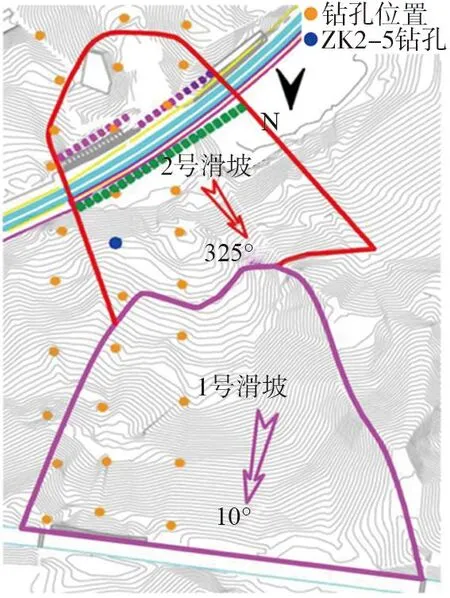
图8 钻孔布设图

图9 深孔测斜曲线

2.2 位移速率曲线分析

分别计算监测期内不同深度处的土体位移速率,并基于深孔测斜曲线特征(图9),分别用不同颜色绘制不同深度区间内的位移速率曲线(黑线:0.5～4.5 m;蓝线:5.0～8.0 m;粉线:8.5～14 m;绿线:14.5～35.5 m),结果如图10所示。由图10(a)可知,速率曲线初期波动起伏很大且曲线分布杂乱无章;后期速率曲线逐渐趋于平缓并有着明显的分簇特征,且不同曲线簇之间近似平行分布。

为了更加清晰地展示不同深度区间处的土体速率特征,分别提取不同区间内的土体速率曲线。由图10(a)～(d)可知:初期滑动面发展变形活跃,外界干扰因素作用显著,不同深度处的土体变形都有着明显的偏移,速率曲线之间相互交错,使得曲线分布整体上显得杂乱无序,而由前面的理论分析可知,滑动面的发展变形会使得不同区间处的土体速率产生显著差异形成曲线簇,且这一特点会贯穿整个滑坡运动过程,故从2018年6月16日—2019年5月15日的速率曲线中亦能隐约分辨曲线分簇特征。

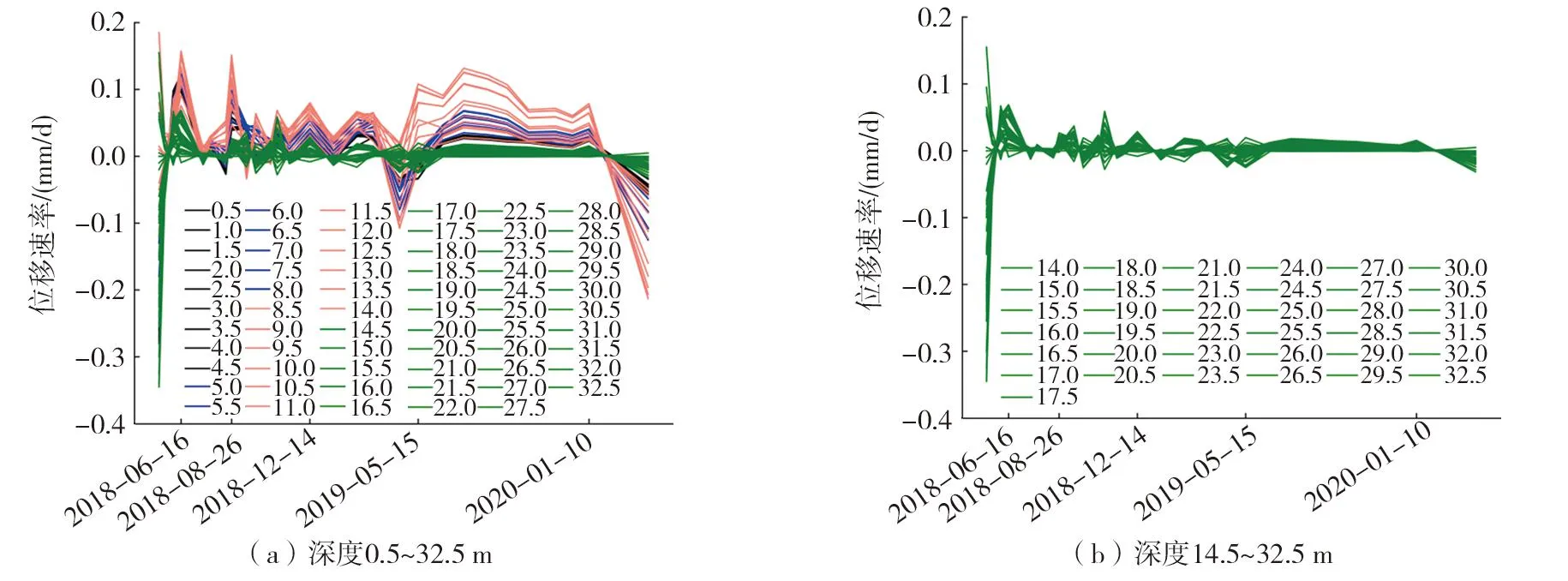
图10 钻孔深部位移速率曲线Fig. 10 Displacement velocity curves of borehole

中后期外界干扰作用减弱,滑动面进一步发展,不同深度处的土体趋向稳定变形,此时坡体变形状态接近概化模型的理想状态,速率曲线之间近似平行分布且具有了明显的分簇特征,且2020年1月10日当日位移速率的曲线分布相对稳定和密集,可明显分为多道曲线簇。

2.3 位移速率散点分析

选取该钻孔监测期内2020年1月10日时坡体不同深度处的位移速率值,以深度为横坐标、位移速率值为纵坐标绘制散点图,如图11所示。

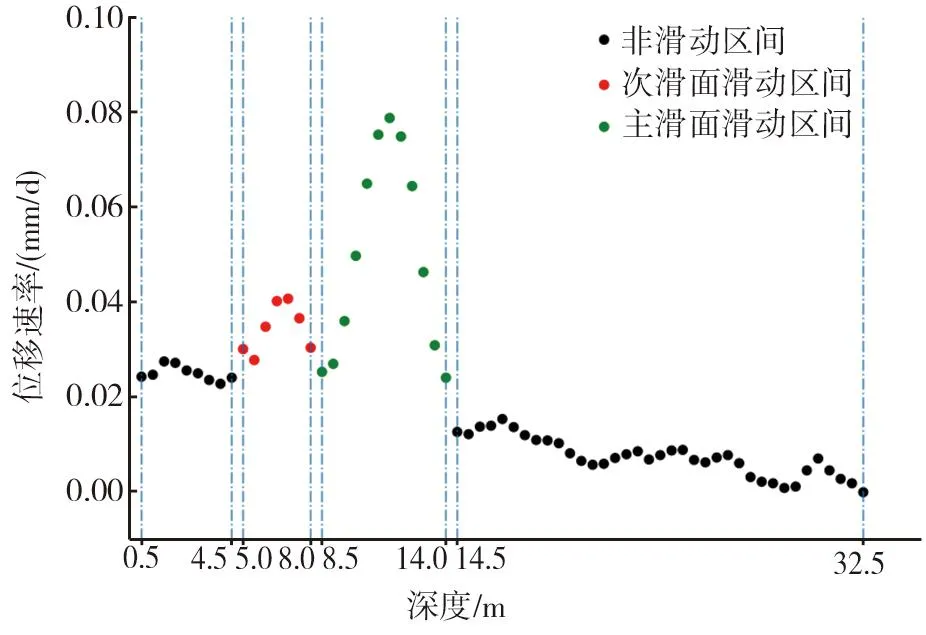
图11 钻孔当日位移速率-深度散点图(2020-01-10)Fig. 11 Scatter plots of displacement velocity-depth on the day of borehole(2020-01-10)

由图11可知:

1)当日位移速率散点具有明显的鼓包凸起特征,形状与概化模型的速率分析结论相对应,且鼓包凸起区间内的速率散点具有明显游离特征,能够有效辨识各滑面所在滑动区间的大致分布范围。其中,次滑面的滑动区间深度大致为5.0～8.0 m,主滑面的滑动区间深度大致为8.5～14.0 m。

2)由于“B”型曲线特征的滑坡体其自身变形具有连续性,各滑动区间的速率散点簇与非滑动区间的速率散点簇彼此之间间隔并不显著,使得滑动区间与非滑动区间两者在交界区域处的速率散点缺乏明显的区分界限,不易辨识该位置处的土体归属区间,影响各滑动区间深度范围确定的准确性。

由上可知,土体位移速率散点分布特征一方面有助于辨识滑动区间大致深度范围,另一方面也存在着区间交界区域处速率散点归属模糊的问题。

2.4 加速度分析

为了能够有效克服散点簇之间间隔不显著、区间交界区域散点归属不清晰的问题,研究结合前面速率曲线的分析结果,基于位移速率进一步提取土体的加速度变化特征。同理,基于深孔测斜曲线特征(图9),分别用不同颜色绘制不同深度区间内的加速度曲线(黑线:0.5～4.5 m;蓝线:5.0～8.0 m;粉线:8.5～14.0 m;绿线:14.5～35.5 m),结果如图12所示。

由图12(a)可知,土体加速度曲线与位移速率曲线相似,初期加速度曲线彼此之间相互交错,加速度曲线整体显得错综复杂。中后期土体加速度趋向稳定,曲线整体贴近于0值,表明监测期内坡体运动并不活跃,土体变形缓慢、运动趋势并不显著。

为了更加清晰地展示不同深度区间处的土体加速度特征,放大中后期的加速度曲线(图12(a)的红色方框区域)变形情况,并分别提取不同区间内的土体加速度曲线。由图12(b)～(e)可知,2019年10月17日的加速度曲线具有比速率曲线更加显著的分簇特征,由上至下存在2个清晰完整的间隔区间将加速度曲线大致划分为三道明显的曲线簇,分别为由绿色和黑色曲线组成的第一道曲线簇(即顶部土体与下部滑床),由蓝色和部分红色曲线组成的第二道曲线簇(即次滑面区间和部分主滑面区间内的土体),以及由剩余红色曲线组成的第三道曲线簇(即主滑面区间内加速度大于次滑面区间的土体)。

图12 钻孔深部位移加速度曲线Fig. 12 Displacement acceleration curves of borehole

选取该钻孔监测期内2019年10月17日时坡体不同深度处的加速度值,由于当日加速度值皆为负值,为了便于分析以深度为横坐标、加速度绝对值为纵坐标绘制散点图,如图13所示。

由图13可知:

图13 钻孔当日加速度-深度散点图(2020-10-17)Fig. 13 Scatter plots of acceleration-depth on the day of borehole(2020-10-17)

1)当日加速度散点具有明显的鼓包凸起特征,且鼓包凸起区间内的加速度散点具有十分明显的游离特征,能够更加准确地辨识各滑面所在滑动区间的深度范围。其中,次滑面的滑动区间深度大致为5.5～8.5 m,主滑面的滑动区间深度大致为9.0～13.5 m。

2)相较于速率散点图,加速度散点图中各滑动区间的散点簇与非滑动区间的散点簇之间存在更大的断层区域,间隔区间更加显著,使得滑动区间与非滑动区间两者在交界区域处的加速度散点具有了清晰明显的区分界限,能够快速准确地辨识该位置处的土体归属区间,解决各滑动区间深度范围模糊的问题,并为滑面位置精准确定提供重要依据。

2.5 滑面位置的精准确定

2.5.1 计算方法选择

提取滑动区间内的加速度散点数据,由于区间内的加速度散点分布特征近似抛物线,且滑面位置处的土体加速度值最大,则基于区间内的散点数据寻找加速度最大值对应的深度是准确辨识滑面位置的关键。而在实际的深孔位移监测中,测斜仪上各测点的间隔距离通常为0.5 m,故此时散点图中滑动区间内最大加速度散点对应的深度并不一定是滑动面的准确位置,仍需基于滑动区间内的加速度散点数据计算加速度最大值及其对应的深度值。

由图13可知,各滑动区间内的数据为离散数据点,故可将“拟合法”和“插值法”作为可行的计算方法,而不同的计算方法有着其各自的适用性。

1)拟合法对于多数据点的计算通常采用高阶多项式拟合,然而这种方法的精度取决于幂次的选择,幂次过低则拟合曲线不能穿越所有数据点且拟合误差大,幂次过高则拟合曲线容易出现龙格现象。由于高阶多项式幂次选择是一个复杂多变的问题,故不适合广泛运用于加速度最大值点的计算。

2)为了能够穿越区间内的所有数据点,并且保持曲线连续光滑的特性,使其符合“B”型曲线的变形特征,可以选择采用三次样条插值法。陈辉[26]基于深孔测斜曲线采用了不同类型的插值法进行计算分析对比,结果表明三次样条插值法的稳定性、贴合度以及精度都是最高的。

该方法的本质是在相邻的数据节点间构成一段三次多项式,再把每一段三次多项式按顺序拼接成光滑的曲线,具有更好的收敛性,能够有效克服牛顿插值法、拉格朗日插值法存在的尖点问题以及多项式阶数过高时存在的龙格现象,且不需要求解过多的导数信息、计算更加简便,适合用于加速度最大值点的计算。

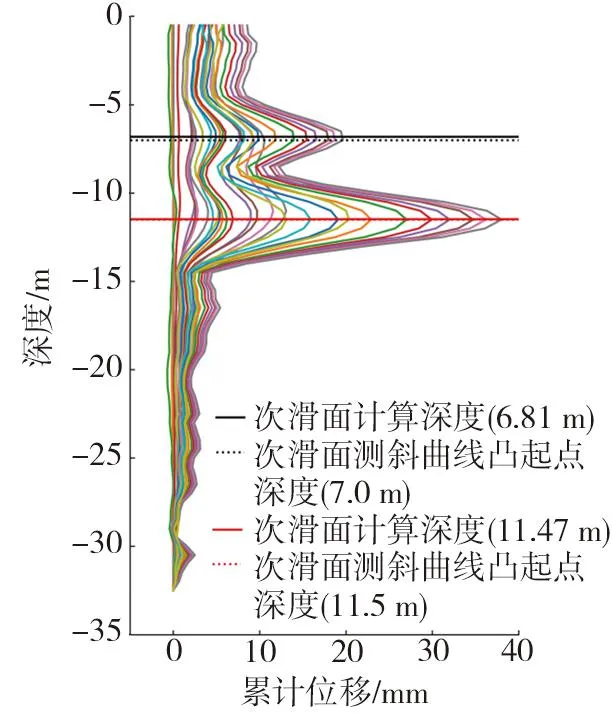
因此,选择三次样条插值法更加符合“B”型曲线滑动区间内离散点的数学运算,其数学计算模型为:假设一系列互不相等的数据节点[xi,yi](i=0,1…n)存在某种关系yi=f(xi),其中a=x0

(1)

式中:j=0,1,…,n-1;hj=xj+1-xj。

2.5.2 滑面位置的计算结果分析

提取次滑面滑动区间内的加速度散点数据,通过Python编程求解该区间内各个区段的三次样条插值函数表达式,结果如式(2)～式(5)所示:

S(5.5-6.5)=-7.58730159×10-5×(x-5.5)3+6.04761905×10-5×(x-5.5)2+ 2.08730159×10-4×(x-5.5)+4.40×10-4

(2)

S(6.5-7.0)=6.03174603×10-6×(x-6.5)3-1.67142857×10-4×(x-6.5)2+ 1.02063492×10-4×(x-6.5)+6.33×10-4

(3)

S(7.0-7.5)=5.17460317×10-5×(x-7.0)3-1.58095238×10-4×(x-7.0)2- 6.05555556×10-5×(x-7.0)+6.43×10-4

(4)

S(7.5-8.5)=8.03174603×10-5×(x-7.5)3-8.04761905×10-5×(x-7.5)2- 1.79841270×10-4×(x-7.5)+5.80×10-4

(5)

由式(2)～式(5)可计算得到次滑面滑动区间内任一深度处的土体加速度,结果如图14(a)所示。同理,可计算得到主滑面滑动区间内任一深度处的土体加速度,如图14(b)所示。

图14 滑面位置计算点Fig. 14 Calculation points of sliding surface position

图15 滑动面位置示意图Fig. 15 Schematic diagram of sliding surface position

由图14可知,次滑面滑动区间处加速度的最大值为0.000649,其对应的深度为6.81m;主滑面滑动区间内的最大加速度为0.001243,对应的深度为11.47m。

将常规的深孔测斜曲线滑面位置辨识方法与本研究提出的计算方法相比较,如图15可知:

1)常规的滑动面位置辨识方法是基于钻孔累积位移-深度曲线(即测斜曲线),通过寻找曲线最大凸起点对应的深度从而确定滑动面的位置,则采用该方法可以得到该钻孔内的主滑面和次滑面分别位于地下11.5、7.0m处。

2)本文提出的计算方法是在累积位移-深度曲线的基础上,通过构建概化模型提取滑动面位置与上下部土体之间的变形关系,建立基于加速度-深度曲线的三次样条插值法,以滑动区间内的加速度最大值作为滑面位置辨识的关键依据,使滑动面的位置可计算化,具有更加科学的数学依据和理论依据。通过计算可以得到主、次滑面的计算深度分别为11.47、6.81m。

此外,由现场钻探报告可知,该钻孔附近的坡体自上至下分别在6.65、11.30m处发现了较为明显的滑动擦痕,则采用常规方法获取的主、次滑面位置误差分别为0.35、0.2m,而本文的滑面位置计算误差约为0.16、0.17m。实际结果表明,研究提出的计算方法能够明显减小常规辨识方法的误差,进一步提升滑面位置辨识的准确度。

3 讨论

3.1 适用性分析

3.1.1 干扰因素及特征搜寻

基于实际案例中土体位移速率和加速度变化规律的分析,可以发现本文提出的概化模型具有一定的代表性和合理性,能够为坡体的运动变化过程提供较为科学的解释。但是,这些规律性的特征显现源于理想状态下的坡体运动,而在实际的深部位移监测过程中,滑坡运动复杂多变,不同深度处的土体位移速率和加速度曲线分簇特征不一定显著,容易受到各种因素的干扰。本研究结合前人的研究成果,将影响滑坡变形主要干扰因素总结归纳为以下几个方面:

1)降雨作用:雨水渗入坡体使得土体重量增加,产生渗透压力弱化了岩体强度,加剧了处于极限平衡状态的坡体向不平衡状态发展,导致坡体稳定性降低。

2)工程扰动:人类工程活动破坏原有的地形地貌,改变了岩体的应力状态,使在自然条件下已经达到平衡状态的岩土体应力进行重新分布,斜坡随之产生新的变形。

3)地质条件:具有松散土层、碎石土、风化壳和半成岩土层的斜坡抗剪强度低,容易随着滑坡的移动产生明显的变形;在各种节理、裂隙、层面和断层发育的斜坡,其滑坡变形也更显著。

因此,在这些干扰因素的影响作用下,土体速率和加速度沿深度方向的分布变得错综复杂,个别位置处的土体甚至会超过滑面位置处的土体速率,使得曲线分簇特征不易辨识。故对于本文提出的方法而言,如何准确寻找曲线分簇特征显著的某日位移速率数据或加速度数据就显得尤为重要。

其中,具有“B”型曲线特征的滑坡其变形是一个缓慢滑移的过程,相较于具有“r”型曲线特征的滑坡其滑面并未完全贯通,而由于其滑面位置处的土体变形大且土体沿深度方向的变形是连续无突变的,使得土体变形近似以滑面位置为凸起点形成多个鼓包。此外,随着时间的推移滑动面不断发展变形,不同位置处的土体位移速率差异愈发显著,而这一特点将会贯穿滑坡的整个运动变形过程。

虽然各种干扰因素的作用容易对土体变形速率产生显著的影响,但是干扰因素的作用往往都是短期间断的,当监测时间足够长时,在监测期内总能找到运动曲线分簇特征明显的时期,受各种因素的影响这个时期往往出现在滑面变形稳定后的中后期。

3.1.2 测点间距及分析指标的影响

在实际的深孔位移监测中,测斜仪上的测点间隔是固定的通常为0.5 m。若在此基础之上进一步缩小测点间隔,对于本方法而言其计算精度虽然能得到进一步提升,但是这种精度的提升并不显著,而且间隔减小对于实际监测而言,就意味着测点数量增多、监测成本上升。

若考虑增大测点间隔,虽然能有效降低监测成本,但也不一定适用于各种类型的滑坡。对于堆填土滑坡和岩石类滑坡而言,其具有滑动面显著、滑带厚度小且滑体以整体运动为主的特点,如果增大测点间隔反而难以确定滑面的准确位置,而且这类滑坡的深孔测斜曲线突变特征十分显著呈明显的“r”型,仅从位移指标就能清晰辨识滑面位置。而对于黏性土滑坡和黄土滑坡而言,这类滑坡的滑带厚度通常较大,在滑面暂未发展贯通时,坡体的移动会带动土体沿深度方向产生连续变形且不易产生突变;另外,本文提出的方法其核心在于计算滑动区间内加速度离散点最大值所对应的深度,若通过物探表明滑带土的分布区间较厚,则离散点的间隔并不会明显阻碍滑动区间内土体变形趋势的体现,即对于最大加速度计算结果的影响相对较小,故可适当放大测点间隔,反之滑带土分布区间较薄,则不宜缩小测点间隔。

3.2 方法优势分析

通过对实际案例的运用分析可以发现,滑动面的实际深度与深孔测斜曲线鼓包凸起点的位置相近,且与加速度最大值处的计算深度基本重合,表明研究提出的方法具有更高的可靠度,可以更加准确地获取滑动面的位置信息。其优势主要体现在以下几个方面:

1)具有更加科学可靠的理论依据。研究基于滑坡体概化模型结合“B”型曲线滑坡体变形特征,考虑不同位置处的土体变形规律,深入分析了模型变形与位移速率及加速度之间的潜在联系,并在实际案例分析中得到验证。

2)充分挖掘“B”型深孔测斜曲线的关键特征,具有广泛的适用性。研究表明不同滑动区间的土体位移速率差异显著,且当滑动面的发展变形达到一定程度时,土体的位移速率沿深度方向会形成明显曲线簇。进一步地,将位移速率转化为加速度,则土体加速度曲线的分簇特征更加显著,能够明显区分土体的滑动区间,可为滑动面位置的准确辨识提供依据。

3)具有合理的数学依据,有着更高的可靠度。研究提出的方法通过提取监测期内曲线分簇特征显著的某日土体加速度数据,运用三次样条插值法计算各滑动面所在滑动区间内的加速度最大值,并以该值对应的土体深度作为滑面的计算深度,从而使滑动面位置的确定可计算化。

基于以上特点,研究提出的计算方法能够有效克服深孔测斜曲线传统辨识方法中存在的滑动面定义不清晰、数值不确定的问题,避免了因观测尺度选取不当导致曲线特征误判以及人为主观判别导致滑面辨识误差较大的情况。

3.3 方法局限性分析

研究提出的方法虽然较好地解决了“B型”曲线在滑动面位置辨识中存在的各种问题,但方法本身也存在着一定的局限性,制约了滑动面计算深度的精度,仍然需要更加深入的研究分析,从而进一步优化计算方法。

1)本文提出的数学计算方法其前提是选择加速度曲线分簇特征显著的某日土体加速度作为分析对象,进而运用三次样条插值法计算当日各滑面所在滑动区间内的加速度最大值,从而确定该值对应的滑动面计算深度。但是监测期内不同深度处的土体速率是动态变化的,不同深度处的土体加速度在不同时期并不相同,使得滑动面的计算深度存在一定的差异。

2)研究提出的计算方法是基于“B”型深孔测斜曲线,不一定适用于其它类型的测斜曲线,但能够为其滑动面位置的确定提供参考。不同滑坡的运动变形过程虽然差异显著,但同样存在一定的共性。对于不同曲线类型的分析,可结合其滑动面的发展程度、不同位置处的土体变形特点,考虑增加约束条件、选取合适的分析指标等建立新的假设条件。

3)由于岩石类滑坡、堆填土滑坡通常具有明显的滑动面、且以整体运动为主,其深孔位移曲线一般不具有“B”型特征;而黄土滑坡和黏性土滑坡在其滑面发展过程中,易随坡体移动产生连续变形呈现“B”型曲线特征。相较而言,本文提出的方法多适用于后者的滑面位置计算分析。

4 结论

基于“B”型测斜曲线变化特征,本文通过构建坡体运动的概化模型,深入分析了土体沿深度方向的变形规律,揭示了不同深度处土体的位移速率和加速度分布特点,为滑动面位置的准确辨识提供了重要依据,提出了一种能够更加准确地辨识“B”型深孔测斜曲线滑动面位置的方法,并在实际的案例中得到了成功运用,主要结论如下:

1)具有“B”型曲线特征的滑坡,土体位移速率曲线沿深度方向的分布具有明显的分簇特征,每簇曲线分别对应各滑面的滑动区间及非滑动区间。将位移速率曲线转化为加速度曲线,则加速度曲线的分簇特征更加显著。

2)基于加速度曲线,提取分簇特征显著的某日土体加速度,加速度-深度散点图具有明显的散点分簇特征,使得各滑面的滑动区间与非滑动区间具有明显的间隔,能够准确划分滑面所在区间的深度范围。

提取滑面所在滑动区间内的加速度散点数据,运用三次样条插值法计算该区间内土体加速度最大值对应的深度,能够更加准确地获取滑动面的具体位置。