基于上限定理确定隧道式锚碇极限抗拔承载力

贺建清,王 津,林孟源,王湘春,范文韬,胡惠华

(1. 湖南科技大学 岩土工程稳定控制与健康监测省重点实验室,湖南 湘潭 411201;2. 湖南省交通规划勘察设计院有限公司,湖南 长沙 410200)

0 引言

锚碇是悬索桥锚固主缆最重要的承载结构,分为重力式锚碇、隧道式锚碇和岩锚锚碇[1],其中岩锚锚碇极为少见。相较于重力式锚碇,隧道式锚碇具有节约材料、经济性好、对地形地貌和周围环境破坏小等优点[2]。隧道式锚碇主体部分主要包括前锚室、锚塞体和散索鞍等。锚塞体嵌固于岩体中,锚固主缆索股,承受主缆拉力,为隧道式锚碇的主要受力构件。实际工程中,最常见、应用最广的锚塞体为沿自身长度方向上小下大、截面呈马蹄形的钢筋混凝土塞形结构[3-6]。锚塞体在悬索桥主缆拉力作用下挤压围岩,周边围岩受挤压作用而处于压剪应力状态,因围岩具有剪胀和应变硬化特性形成夹持效应,使得隧道式锚碇能够承受巨大的主缆拉力[7]。

由于锚塞体与围岩相互作用机理的复杂性,目前对隧道式锚碇的认识尚不够深入,隧道式锚碇的设计理论也不够成熟,对于如何确定隧道式锚碇极限抗拔承载力还缺乏一个统一的共识[8-9]。现行JTG/T D65-05—2015《公路悬索桥设计规范》[1]没有给出明确的隧道锚抗拔承载力计算公式,但在推荐的锚塞体抗拔安全系数计算公式中,将隧道式锚碇视作重力式锚碇,利用自重、锚塞体与围岩接触面的摩擦力、黏聚力来平衡主缆拉力,未考虑因围岩夹持效应形成的巨大抗拔力,导致锚塞体抗拔安全系数偏低[7]。

迄今,确定隧道式锚碇极限抗拔承载力主要有2条途径:一是在隧道式锚碇设计地址附近选择工程地质条件、岩体结构特性相近的场地,按一定相似比例现场制作缩尺模型,通过拉拔试验确定隧道式锚碇的极限抗拔承载力[10-13];二是考虑隧道式锚碇的抗拔作用机理与抗拔桩和锚杆(索)类似,参照已有的抗拔桩或锚杆(索)的相关研究成果,针对隧道式锚碇在极限状态下可能出现的破坏模式,基于极限平衡理论推导出隧道式锚碇极限抗拔承载力的计算公式[14-17]。前者直观可靠,但工程大、耗时长和费用高;后者只是相对满足了其平衡条件,忽视了岩体运动条件。

本文在分析总结隧道式锚碇破坏模式的基础上,针对隧道式锚碇最可能发生的破坏模式,将破坏体视为以锚塞体中心线为轴线的旋转楔形体,假定破坏面为最小旋转曲面,利用变分法经典欧拉方程求解破坏体最小旋转曲面问题,确定旋转曲面母线方程,基于改进的Mohr-Coulomb强度准则,由主缆拉拔荷载和楔形体自重所做的外功率与楔形体沿滑移面所消耗的内功率相等的条件建立虚功方程,推导隧道式锚碇的极限抗拔承载力上限解。并且,开展室内模型试验,研究隧道式锚碇拉拔承载过程中坡面位移的变化规律,确定隧道式锚碇的破坏模式,验证其极限抗拔承载力计算公式的合理性。

1 隧道式锚碇破坏模式

自隧道式锚碇技术在悬索桥工程应用以来,尚未出现失稳破坏的实例。已有的研究认为,当围岩完整性较好、强度高,隧道锚埋深较大,且锚塞体与围岩接触界面的结合程度较低时,在主缆拉力作用下,当锚塞体与周边围岩接触面的剪切力达到极限状态,锚塞体易沿接触面滑移,发生如图1(a)所示锚岩接触面滑移破坏;当围岩完整性较差、强度较低,节理裂隙发育,且隧道锚埋深较小,但锚塞体与围岩接触面结合程度较好时,当围岩体内某一点达到了屈服极限并自该点产生了裂隙,随着荷载逐渐增大,裂隙沿着荷载方向和锚塞体环向逐渐扩散并贯通,最终形成底部小顶部大的楔形破裂体,发生如图1(b)所示围岩倒楔形冲切破坏[8]。

图1 隧道式锚碇破坏模式Fig.1 Failure modes of tunnel anchorage

隧道式锚碇位置一般选择岩体完整稳定的区域。国外多在围岩成洞条件好,适于减小洞身规模,发挥围岩受力的情况下采用。国内隧道式锚碇多集中于西南山区,因受地形地貌条件限制,总体上地质条件、围岩完整性较差,所以国内隧道式锚碇多位于岩溶发育或破碎底端,且尺寸规模较大。因为先进的现代施工技术可以充分保障锚塞体与围岩接触面的施工质量,隧道式锚碇如果发生破坏,很难出现锚岩接触面滑移破坏,更多的是围岩倒楔形冲切破坏[1]。

2 隧道式锚碇极限抗拔承载力上限解

2.1 基本假定

根据隧道式锚碇可能出现的倒楔形冲切破坏模式,建立计算模型如图2所示。

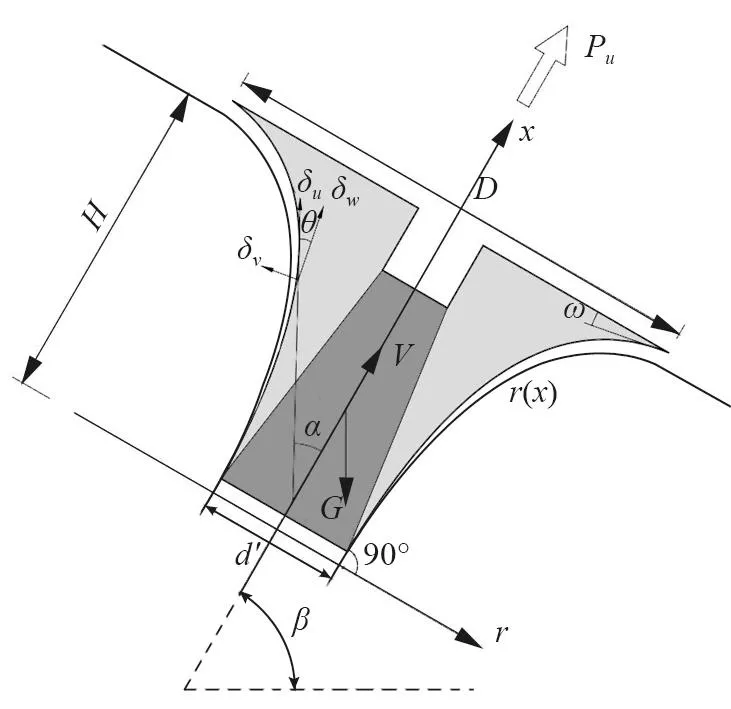
图2 隧道式锚碇计算模型Fig.2 Calculation model of tunnel anchorage

为计算方便,将锚塞体马蹄形截面等效为圆形截面,锚塞体视为上小下大的圆台体,同时作出如下假定:

1)锚塞体及周边围岩皆为均质各向同性材料。

2)将破坏体视为以锚塞体中心线为轴线的旋转楔形体,楔形体母线与坡面、锚塞体底平面夹角分别为ω=45°-φ/2[18]和90°,破坏面为最小旋转曲面。

3)主缆拉拔荷载由锚塞体周边围岩抗剪力提供。

4)假定锚塞体围岩体为理想的刚塑性材料,破坏机制服从改进的Mohr-Coulomb强度准则,楔形冲切破坏体沿破坏界面发生简单平行滑动。

将锚塞体马蹄形截面面等效为圆形时,可按式(1)进行转换:

(1)

式中:A′为锚塞体马蹄形截面面积;d′为等效换算后所得圆形截面直径。

2.2 用变分法经典欧拉方程求解最小旋转曲面问题

设楔形破坏体截面半径r为x的函数,由图2几何关系,可得

(2)

(3)

(4)

楔形体绕x轴旋转面积函数S为

(5)

设

(6)

则欧拉方程为[19]

(7)

对式(6)求偏导得

(8)

将式(8)代入式(7)可得

(9)

由式(9)两边求平方、整理得

(10)

对式(10)两边求导得

(11)

若r′=0,则r(x)=C。C为常数,不符合该假定的破坏模型,故舍去。

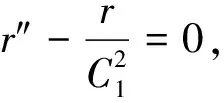
r(x)=a·ex/C1+b·e-x/C1

(12)

由假定条件2)可知:

(13)

(14)

(15)

借助Matlab编程,将公式代入程序,利用计算机程序逐一搜索问题域的解空间内所有的解,并根据给定条件选择符合要求的解,得C1值,得已知参数,设该参数为B,得楔形旋转体母线方程为

(16)

2.3 楔体破坏面能量耗散率

通过围岩和混凝土的试验研究发现,Mohr-Coulomb强度准则可在破坏情况下得到合理应用。但按此强度准则,岩石破坏时的最大主拉应力会随平均应力的增加而增加。这个结果与试验得出的结果相矛盾,因为实际经验中,拉伸方向垂直的正应力分量并不会影响拉伸强度。因此选择改进库仑准则,从而使围岩承载力计算中考虑到拉伸强度和局部可变性的影响[20]。图3所示为一个带有圆端头、拉应力小但非零的拉伸截断Mohr-Coulomb强度准则,同时给出了无围压和单向拉伸的莫尔应力圆。应力圆与横轴的交点到坐标原点的距离分别为σc和σt。

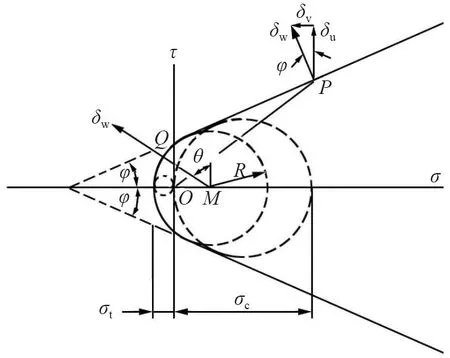
图3 改进的Mohr-Coulomb强度准则Fig.3 Modified Mohr-Coulomb strength criterion

(17)

(18)

(19)

σ=R-σt-Rsinθ

(20)

(21)

则联立式(17)～式(21)可得

(22)

对于采用改进的Mohr-Coulomb强度准则的岩石材料,它的破坏面相对速度夹角θ不仅与其自身有关,而且与滑动破坏面的法向应力有关,随着主应力的增加,夹角也趋近于φ。这样,对于简单滑动的特殊情况,夹角θ的值可与φ取相同值。

根据假设4)即楔形体沿破坏面仅发生简单平行滑动,可令θ=φ,则式(22)可简化为

(23)

根据岩体极限平衡条件可知

(24)

根据图2所示计算模型的几何关系及假设4)可得

(25)

将式(24)、式(25)代入式(23)得

(26)

沿整个楔体破坏面的能量耗损率为

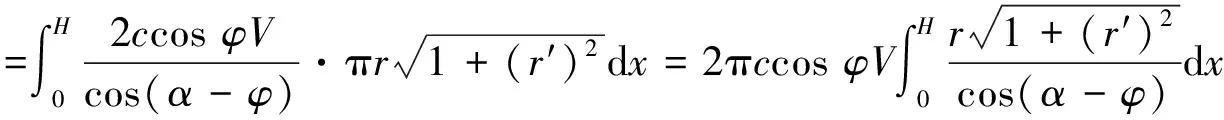
(27)

2.4 抗拔承载力上限解

当楔形体因冲切破坏发生微小移动时,假设楔形体沿外力方向的速度为V,则外力所作功率W外为

W外=(Pu-Gsinβ)·V

(28)

式中:G为楔形破坏体重量;β为锚塞体轴线与水平面的夹角;α为锚塞体轴线与破坏面切线的夹角。

当外力所作功率W外与沿破坏面的能量耗损率W内相等时,结构可视为达到了极限条件。由内外功率互等可得方程为

W外=W内

(29)

即

(30)

联立式(16)和式(30)求解得隧道式锚碇极限抗拔承载力Pu表达式为

(31)

其中

α=arctan(r′)

(32)

3 隧道式锚碇拉拔承载试验研究

为了研究隧道式锚碇可能的破坏模式,验证其极限抗拔承载力计算方法的合理性,开展了隧道式锚碇室内模型试验。

3.1 锚塞体及其围岩制备

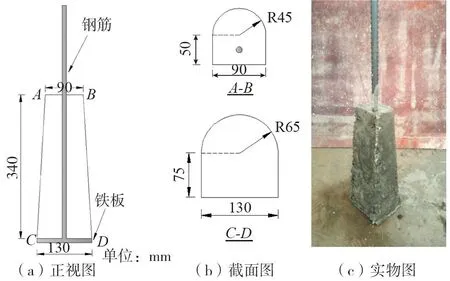
图4 脱模锚塞体Fig.4 Demoulding anchor body

选用水泥、砂、红黏土、石膏和水5种常见的材料按照4∶45∶1∶1∶9的配合比拌合、浇筑模拟锚塞体围岩,养护2周后经试验测得其力学参数如表1所示。

表1 模拟围岩力学参数Table 1 Mechanical parameters of simulated surrounding rock

3.2 模型箱制作

采用胶合板与钢架制作四周封闭的可拆卸模型箱,模型箱尺寸为1 m×1 m×0.8 m,两侧钢架上放置工字钢作为反力架。在工字钢上焊接中部开圆孔的铁板以便放置锚杆拉拔仪,施加拉拔力。模型箱如图5所示。

图5 模型箱Fig.5 Model box

3.3 试验加载及变形量测

在隧道式锚碇模型试验中后推法和前拉法是较为常见的 2种加载方式。后推法是将锚塞体放置于千斤顶的前端,千斤顶借助后方反力支架来实现对锚塞体底部施加荷载,使锚塞体向外侧移动直至破坏。该方法虽然设计操作简单且锚塞体受力均匀,但因为需要在锚塞体后方设置千斤顶等装置,需要在锚塞体底部预留较大范围空间,与实际工程存在一定偏差。

前拉法有通过钢线一头连接锚塞体,利用反力架上的滑轮控制加载方向,另一头放置不同重量的砝码来达到分级加载效果。此外还有借助反力梁用锚杆拉拔仪张拉施加荷载的方法,其作用方式与锚杆拉拔相似。该方法施加荷载时可模拟实际工程中主缆拉力作用,相比后推法可保留锚塞体底部附近围岩以观测其破坏。

模型试验中不考虑锚塞体自身应变破坏,未对其进行变形监测。坡面位移通过布置百分表读取加载全程位移变化,以钢筋为中心周边一定范围内,取100 mm间距横纵双向布置百分表,利用磁性表座将百分表固定在钢支架上,每级加载稳定后记录各监测点位移量,百分表布置如图7所示。其中监测点1至监测点5布置在1-1′方向,亦即水平方向;监测点6至监测点10布置在与1-1′方向正交的2-2′方向。

图6 模型试验加载示意图

图7 百分表布置示意图

3.4 试验步骤

将锚塞体钢筋穿过工字钢与铁板,固定锚塞体至预定位置。将配合比符合要求的填料,逐层浇筑于模型箱中,每一层填料浇筑完毕并用振捣棒振捣密实后,方能浇筑上一层。填料全部浇筑完成后,静置2周,开始试验。用室内起重机吊起模型箱一侧使模型箱整体倾斜至底面与水平面夹角呈30°,固定模型箱。安装百分表,测读初始读数。将已标定锚杆拉拔仪穿过伸出反力架及铁板的锚塞体钢筋并套上锚具张拉锁定,按照JGJ/T 401—2017《锚杆检测与监测技术规程》[22]进行拉拔试验。每级荷载加载完成且读数稳定后记录各监测点的数据,直至锚碇破坏后停止加载。正在进行隧道式锚碇拉拔试验如图8所示。

图8 隧道式锚碇拉拔试验Fig.8 Pull-out test of tunnel anchorage

3.5 试验结果分析

坡面不同测点在各级荷载下的位移量因位置不同而不同。根据监测点3即拉拔作用点的位移量绘制的荷载-位移曲线如图9所示。

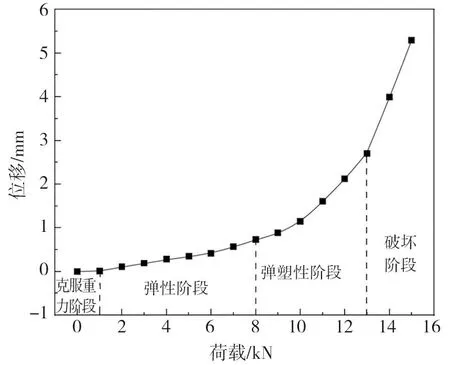
图9 荷载-位移曲线Fig.9 Load-displacement curve

根据荷载—位移曲线,拉拔作用点在试验加载过程中各阶段的位移变化特征可分为如下4个阶段:

1)由初始状态加载至1 kN,坡面仅产生微小位移,该阶段可视为锚塞体在拉拔荷载下克服自身重力的过程,为室内模型试验的初始阶段,锚塞体通常不受外力荷载影响,开始加载后需要首先平衡自身重力,该阶段持续时间较短。

2)荷载由1 kN加载至8 kN,曲线斜率较小且平缓,呈线性变化。该过程的荷载属于隧道式锚碇正常工作的容许荷载,位移变形量在安全范围内,该阶段可视为隧道式锚碇的弹性阶段。

3)荷载由8 kN加载至13 kN,坡面位移量明显增大,其斜率随荷载的增加而增大,可由此判断在荷载作用下隧道式锚碇产生了破坏趋势,该阶段可视为隧道式锚碇的弹塑性阶段。

4)荷载加载超过13 kN后,坡面位移增量发生突变,位移曲线陡升。表明隧道式锚碇已发生破坏,失去承担拉拔荷载的能力,隧道式锚碇模型极限抗拔承载力约为13 kN。

因加载至8 kN前坡面位移变化量较小,若将曲线全部绘出不便于观察其位移变化,为此,只绘出部分荷载下的位移变化曲线,坡面位移变化曲线图如图10所示。

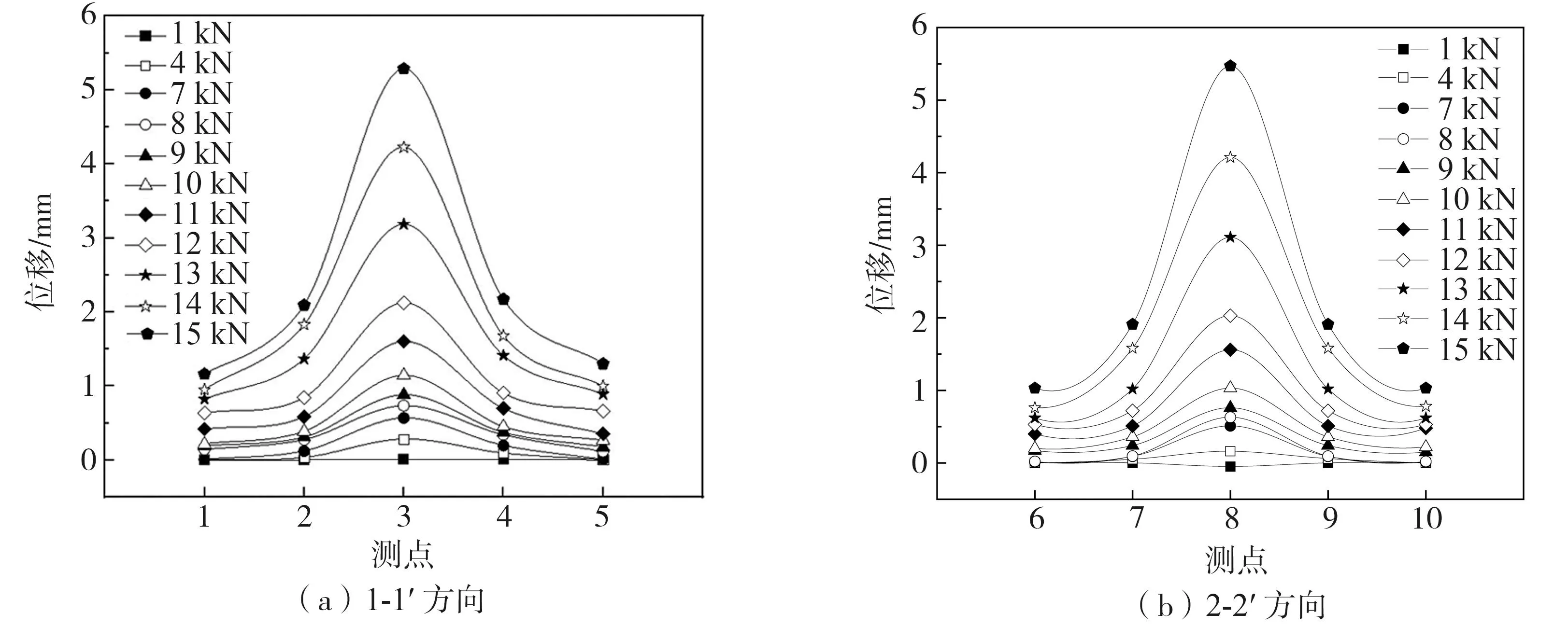
图10 坡面位移变化曲线图Fig.10 Slope displacement variation curves

由坡面位移变化曲线可知,坡面位移在1-1′方向大致呈对称分布,随着离中心点距离的增加急剧衰减,最大值位于拉拔作用点。荷载加载至8 kN前,仅中心点能看出较明显的位移,中心点周边100 mm范围内的位移较小,在100～200 mm范围内位移极小可忽略不计,在200 mm范围外的坡面并未受到荷载影响。荷载加载至8 kN后,中心点位移变化较大,在曲线中表现为明显的向上凸起,整体曲线呈中间突出的坡状。距离中心100 mm范围内的坡面位移皆超过0.1 mm,距离中心200 mm的位置也出现了较为明显的位移变化。荷载加载至13 kN后,中心点位移的增长速度发生突变。此时坡面的位移曲线呈现“倒V形”分布,该形状与锚塞体被拔出时将其顶部范围内的围岩向周边顶开时的现象类似。

坡面位移在竖直方向的变化规律与水平方向略有不同,受重力影响,坡底一侧位移略大于坡顶一侧。

3.6 破坏模式分析

当加载至极限荷载之后,坡面位移量发生突变,围岩表面出现以钢筋为中心向四周扩散的微小裂痕,最终模型破坏时表面的微小裂痕扩大变为数条明显的大裂缝并向外延伸,表面整体破坏范围呈圆形,锚塞体被向外拉出。将锚塞体与破碎岩土体取出后,其孔洞如图11所示。

图11 锚塞体围岩破坏Fig.11 Destruction of surrounding rock of anchor plug body

锚塞体取出后,观察其自身并未发生结构破坏,围岩破坏区域主要集中于锚塞体上部一定范围内,锚塞体底部围岩以及锚岩接触面有小范围破坏,但整体破坏面与锚塞体形状接近。至于围岩周围出现大裂缝是因为在拉拔力作用下,锚塞体挤压围岩,沿径向产生拉应力,当拉应力超过围岩抗拉强度,围岩拉裂进而产生放射状裂缝,此现象在今后的研究中有待进一步考虑。

为进一步观测整个楔形体的形状,以破裂后的围岩模型作为模具,将孔洞内破碎围岩清理干净,用透明薄膜紧贴孔壁覆盖,拌合一定量的混凝土,将其浇入围岩孔洞,待混凝土达到定强度后将成型混凝土楔体取出,如图12所示。

由图12(b)中可知,楔形体底部有向下的轻微凸起部分,可判断在施加荷载过程中锚塞体底部附近围岩产生了破坏。中下部破裂形状大小与锚塞体接近,两侧曲线向外略微倾斜。楔形体上部在接近锚塞体顶部附近的深度位置,曲线斜率发生突变并向两端延伸直至到达破裂体上表面,整体呈喇叭状。

图12 破裂楔形体制作流程图Fig.12 Manufacturing flow chart of broken wedge

3.7 抗拔承载力分析

由试验结果得知该隧道式锚碇模型极限抗拔承载力约为13 kN,为验证本文推导所得计算式的合理性与可行性,以模型试验为算例,采用本文方法计算极限抗拔承载力,并与文献[8]的传统极限平衡方法、文献[23]的考虑夹持效应改进的极限平衡方法以及将文献[24]的破裂体转化为圆台的极限分析方法得到的计算结果进行对比。计算结果如表2所示。

由表2可知,文献[8]方法计算值明显低于其他结果,本文方法、文献[23]方法以及文献[24]方法的结果较为相近且本文方法拥有较高的上限值。一方面是因为文献[8]方法仅相对满足了平衡条件,忽视了岩体运动条件,另一方面未考虑因围岩夹持效应形成的巨大抗拔力,导致锚塞体抗拔承载力计算结果偏低。根据现有诸多加载至破坏的室内模型试验可知,隧道式锚碇发生围岩倒楔形破坏时曲面破坏更为常见。在实际工程应用中虽可将曲面破坏的喇叭状简化为圆台状,但对比本文方法和文献[24]方法可看出在将破裂体转化为圆台状后,破裂体的面积以及体积相比实际会偏小,导致计算值与实际存在偏差。因此,按重量进行等效转换虽有利于工程应用计算,但在对倒楔形破坏模式进行研究时将破坏面视为旋转曲面的方法更为严谨。

表2 计算结果对比Table 2 Comparison of calculation results

此外,不论是本文方法还是考虑夹持效应改进后的极限平衡方法同传统极限平衡方法相比,计算所得的计算结果都相差较大。可见,传统极限平衡方法虽然在相对简单的锚岩接触面破坏模式中适用性较好,但是在破坏模式复杂、不确定因素较多的围岩倒楔形破坏模式中难以适用。

4 结论

本文在分析隧道式锚碇破坏模式基础上,改进极限抗拔承载力确定方法,并开展隧道式锚碇室内模型试验,得出以下结论:

1)将破坏体视为以锚塞体中心线为轴线的旋转楔形体,假定破坏面为最小旋转曲面,利用变分法经典欧拉方程求解最小旋转曲面问题,确定旋转曲面母线方程。基于改进的Mohr-Coulomb强度准则,采用极限分析方法推导出隧道式锚碇极限抗拔承载力的上限解,因为这种方法假定破坏面更接近于破坏实际情况,其计算所得结果更为精确。

2)开展隧道式锚碇室内模型试验,得到了坡面不同测点在拉拔承载过程中的位移变化曲线,拉拔作用点的荷载-位移曲线可分为4个阶段:克服重力阶段、弹性阶段、弹塑性阶段以及破坏阶段。以拉拔作用点为中心,坡面位移在水平方向大致呈对称分布,随着离中心点距离的增加急剧衰减,最大值位于拉拔作用点;坡面位移在竖直方向的变化规律与水平方向略有不同,受重力影响,坡底一侧位移略大于坡顶一侧。隧道式锚碇破坏模式为围岩倒楔形冲切破坏,破坏体可近似视为以锚塞体中心线为轴线的旋转楔形体。

3)将本文所得隧道式锚碇极限抗拔承载力计算公式计算值、已有类似公式计算值与模型试验实测值进行对比,发现极限平衡法因其相对满足平衡条件,在破坏形式与结构复杂的倒楔形破坏模式下存在一定不足,选用具有严格塑性理论依据的极限分析方法或考虑围岩夹持效应的极限平衡方法求得的极限抗拔承载力理论值与实测值一致性较好。受时间和经费限制,只开展了1组模型试验,实际破坏数据太少,虽然破坏面形状的假定与本文试验以及承载机理相似的桩锚拉拔试验结果一致,但仍有待今后的研究中进一步完善。