基于三角模糊数序贯博弈的电网安全研究
洪 超,施宇锋,匡晓云,许爱东,张宇南
(1.南方电网科学研究院有限责任公司,广东 广州 510663;2.浙江腾珑网安科技有限公司,浙江 杭州 311225)
0 引言
智能电网是关键信息基础设施。因此,智能电网监控系统攻防研究具有十分重要的战略意义和现实意义。
近年来,智能电网网络安全事件频发,黑客或敌对势力利用智能电网中工艺、参数以及操作等漏洞,攻击电网物理生产装置并导致电网瘫痪[1]。2015年,乌克兰电力系统遭受BlackEnergy攻击,导致大面积停电、约140万人受到影响[2]。2016年,Industroyer病毒利用电力协议实现对断路器的控制,使得电网级联故障,甚至造成设备损坏[3]。文献[4]提出通过挖掘IEC 61850协议脆弱性,可以实现电网攻击。虽然针对智能电网攻击事件的研究已经有很多,但是使用博弈理论和策略方法对智能电网的攻防研究很少。
博弈论是研究多个个体或团队之间在特定条件制约下寻求最优策略的理论,广泛应用于网络安全攻防行为策略研究。文献[5]构建基于Q学习算法的网络状态转移与演化博弈方法,以有效识别电网调度网络安全态势感知。文献[6]针对智能电网信息和物理博弈,提出了一种贝叶斯序贯博弈模型,根据序贯博弈树得到博弈双方攻击者的最优攻击策略和防护者的最优防护策略。文献[7]提出三角模糊数的博弈算法,以提高网络攻防评估结果的准确性和有效性。
本文研究智能电网工控网络安全博弈时,针对博弈双方网络安全属性难以用精确数值表示的问题,提出了一种将三角模糊数应用到序贯博弈的算法,得到智能电网网络安全攻防双方最优攻防策略,从而保障智能电网网络安全运行和防护。首先,本文结合智能电网网络攻防双方特点,构建网络攻防轮流策略的序贯博弈模型。接着,本文采用三角模糊数攻防效用权益方法对网络安全属性进行模糊化处理,从而得到序贯博弈最优攻防策略。最后,本文对智能电网网络安全博弈进行仿真试验,验证了模型和算法的准确性及有效性。
1 智能电网序贯博弈模型
智能电网由数据采集和监控、远程终端、继电保护装置、故障录波以及一次设备等组成,实现对电网遥测、遥信、遥控、遥调等调度和电力输送。当前,由电网工控网络脆弱性引起的恶意事件越来越多,但对智能电网攻击和对应的防护策略研究较少。因此,使用博弈理论分析智能电网安全以及电网攻防策略的研究具有创新意义。智能电网博弈由攻击者、防御者、安全防御机制等组成。攻击者和防御者根据电网变化调整自身的策略,选择对自身收益最大的策略进行博弈。智能电网安全博弈如图1所示。
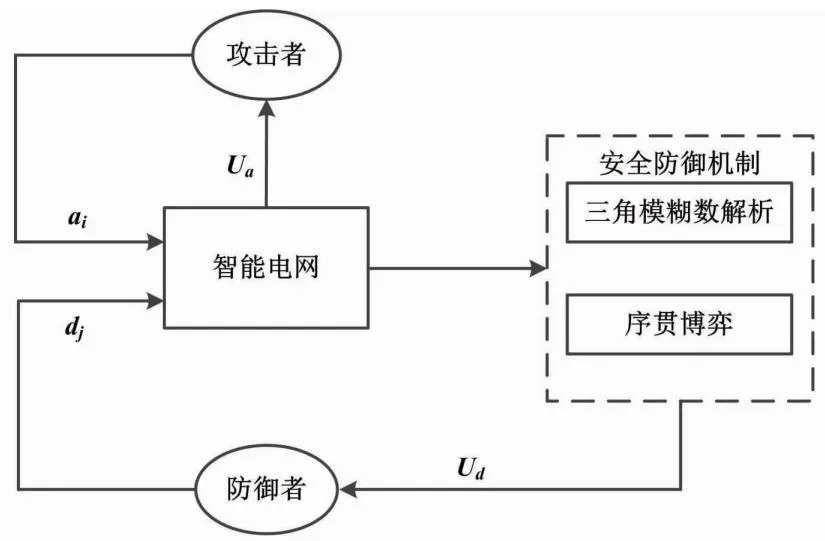
图1 智能电网安全博弈图
智能电网通过序贯博弈进行攻击和防御博弈。其中:Ua、Ud分别为攻击者和防御者功效收益集;ai、dj分别为攻击者、防御者策略。
1.1 智能电网博弈模型
博弈模型是一个四元组G=
①系统损失(system damage,SD)指博弈双方攻防对目标系统资源造成的损害程度,通常由可用性A′a、完整性Ia、机密性Ca组成。
(1)
式中:ρe为被攻击者利用概率的属性;ωa、ωi、ωc分别为可用性、完整性、机密性属性的代价权重系数,ωa+ωi+ωc=1;m为攻击数量;Sd为SD;d为博弈树深度。
②攻击成本(attack cost,AC)指攻击者为发现和利用攻击需要消耗的成本。不同水平的攻击者使用同一资源消耗的成本不同。攻击成本Ac主要是攻击操作成本Ao。
Ac(a)=Ao(a)
(2)
③防护成本(defence cost,DC)指目标系统受到攻击采取的防护策略需要消耗的成本。防护成本Dc主要是防护操作成本Do。
Dc(d)=Do(d)
(3)
④攻击效用(attack effect,AE)指攻击者对目标系统造成的损害程度。攻击效用Ua(a)为:
Ua(a)=Sd(a)+Ac(a)
(4)
⑤防护效用(defence reward,DR)指目标系统遇到攻击时采取的防护策略获得的收益。防护效用Ud(d)为:
Ud(d)=Sd(a)+Dc(d)
(5)
1.2 智能电网序贯博弈模型
智能电网安全博弈是攻击者和防御者之间的双人博弈。博弈参与者决策有先有后。后决策的参与者知道先决策的参与者做出的决策。这种决策称为序贯博弈。攻击者和防御者之间轮流选择策略,可以用博弈树表示。
序贯博弈攻击效用Ua(a)和防护效用Ud(d)是系统损失Sd加上攻击者或防御者收益。
(6)
序贯博弈双方攻击者和防御者策略集合为S′=(A′a,A′d)。
由于序贯博弈攻击者和防御者轮流采取策略,当攻击者策略为A′a且博弈方为攻击者时,博弈行为收益是博弈树深度d乘以攻击者成本;当博弈方为防御者时,博弈行为收益为负的博弈树深度d乘以防御者成本;当防御者策略为A′d且博弈方为攻击者时,博弈行为收益是0;当博弈方为防御者时,博弈行为收益为博弈树深度d乘以防御者成本。
纳什均衡存在性为:博弈四元组G=
因此,智能电网博弈可以用攻击者和防御者的概率来确定纳什均衡解,并确定攻击者和防御者的类型。
1.3 三角模糊数算法
攻击者和防御者的攻防双方SD很难用确定的计算式计算,因此,本文引入三角模糊数的方法。本文通过攻防双方的网络安全属性值来获得三角模糊数,进而非模糊化确定SD。
三角模糊数为M(l,m′,u)(0 (7) 式中:m′为三角模糊数M的主值;l为三角模糊数M的下界;u为三角模糊数M的上界。 三角模糊数M的下限为(m′-l)、上限为(m′-u)。(u-l)的值越大,则表示三角模糊数M的模糊程度越大。在网络攻防环境下,三角模糊数上界u和下界l分别表示攻防参与者对收益的最大可能值和最小可能值,则m′为最可能值。 p=(pl,pm′,pu)用于表示三角模糊数M的概率。本文根据l、u与m′的偏离程度,确定m′的可能性,即m′的可能性为l的倍数N。同时,m′的可能性为u的倍数。三角模糊数概率为pl、pm′、pu。 (8) 式中:pl+pm′+pu=1,pl>0,pm′>0,pu>0。 序贯博弈攻防SD使用三角模糊数转化为非模糊化的三角模糊数M的均值来表示。由M的概率可得均值E(M)。 E(M)=pl×l+pm′×m′+pu×u (9) 序贯博弈各方的决策不是同时进行,而是按一定顺序选择战略,并实施最优策略。因此,本文序贯博弈基于博弈树由攻防双方依次轮流采取策略。攻防双方先后采取一次行动后,用所构成的一组新的子博弈来计算。计算方法采用博弈树逆向归纳法。序贯博弈数值可以用攻防效用(即系统损失Sd加上攻击者或防御者收益)求得。 三角模糊数序贯博弈算法步骤如下。 ①初始化。 本文初始化可用性、完整性、机密性的权值ωa、ωi、ωc。同时,博弈树攻击者和防御者效用初始化为(0,0)。 ②建立序贯博弈树。 根据序贯博弈四元组G= ③建立三角模糊数和非模糊均值。 根据式(7)~式(9),计算三角模糊数、模糊概率分布和非模糊数均值,确定系统损失Sd值。 ④建立序贯博弈攻击者或防御者效用。 以清晰化的均值作为SD,加上攻击者或防御者行为收益,求得博弈树的每个节点的效用。前者为攻击者的效用。后者为防御者的效用。 ⑤迭代。 代码如下。 fori=0;i≤d;i++;do if决策节点为攻击者轮次then比较后续分支的攻击者的效用,保留攻击者效用较大的行为为策略; end if if决策节点为防御者轮次then比较后续分支的防御者的效用,保留防御者效用较大的行为为策略; end if end for。 随着电网工控系统网络安全威胁日益突出,电网数据采集与监视控制(supervisory control and data acquisition,SCADA)、远程终端、继电保护装置等控制器的公用/私用协议和漏洞机理都有可能诱发攻击行为。若同时结合工艺业务场景脆弱性以及工艺互锁等,可能使得电网负荷切投潮流、电压/电流数据值变化、断路器/刀闸合闸/跳闸动作以及状态变位等,从而造成电网临界状态转变、电网设备瘫痪、设备损毁[9-10]。为了验证本文提出的三角模糊数序贯博弈模型和算法的有效性,本文以智能电网网络安全模型进行验证。 通过三角模糊数序贯博弈对智能电网进行攻击者和防御者策略分析,建立攻防双方行动空间。其中,电网网络攻击者使用遥信欺骗(ars)、控制接管(arc)、工艺互锁(ate)等策略,不攻击策略为ano;电网网络防御者采取工控威胁感知策略(dtp),不防御者策略为dno。本文设智能电网网络攻击者AC为ars=3、arc=5、ate=60、ano=0;防御者行动的DC为dtp=4、dno=0。 三角模糊数序贯博弈双方首先采取攻击者策略,然后使用防御者策略依次轮流行动,最后采用数值算法进行攻防双方效用分析。其中:三角模糊数序贯博弈树攻击者为实心圆;防御者为空心圆;博弈树根节点攻防效用初始化为(0,0)。博弈树高度0层为攻击者,左侧为ars,右侧为ano;高度1层为防御者,即dtp和dno;高度2层为攻击者,即ate和arc。本文根据智能电网序贯博弈树,通过三角模糊数式(7)~式(9)和表1进行攻防效用计算。 表1 攻防损失效用 本文智能电网的Sd用安全属性表示,包括可用性、保密性和完整性。其安全属性权重为ωa=0.3、ωi=0.4、ωc=0.3。由于智能电网的Sd很难用精确数值表示,因此用三角模糊数来表示智能电网SD,以求得攻防效用。每个安全属性都规定了影响级,分别为严重(30~20)、中等(19~10)、轻微(9~0)。不攻击或不防御时攻防效用为零。计算得到的攻击模糊化攻防效用值,可使用严重、中等、轻微表示。智能电网的攻防损失效用如表1所示。 表2 攻击者去模糊化的攻防效用 依据去模糊化均值得到Sd,由式(6)可得攻防序贯博弈中的攻击者效用Ua(a)和防御者效用Ud(d),即(Ua,Ud)。攻防效用如表3所示。 表3 攻防效用 智能电网三角模糊数序贯博弈和贝叶斯序贯博弈,即用逆向归纳法从最后一个决策点开始,找到第一个决策点的最优行动选择和路径,并依次找到攻防双方最优决策。智能电网攻防序贯博弈树如图2所示。 图2 智能电网攻防序贯博弈树 图2中,序贯博弈树有三层:第一层由攻击者ars和ano进行博弈;第二层由防御者dtp和dno进行博弈;第三层由攻击者ate和arc进行博弈。 首先,最后决策是攻击者轮次:左侧攻击者效用为ate和45.83、arc和35、ate和39.83、arc和30.17,则左侧攻击者最优策略和效用是ate和45.83;右侧攻击者最优策略和效用是ate和43.17。 其次,博弈树深度1是防御者轮次:左侧防御者最优策略和效用是dtp和9.83;右侧防御者最优策略和效用是dtp和7.17。 最后,博弈树深度0是攻击者轮次:左侧攻击者最优策略和效用是ars和45.83;右侧攻击者最优策略和效用是ano和43.17。因此,攻击者最优效用为45.83。 本文基于贝叶斯序贯博弈模型对智能电网网络安全进行博弈和均衡策略分析[6]。智能电网攻防贝叶斯序贯博弈树如图3所示。 图3 智能电网攻防贝叶斯序贯博弈树 通过序贯博弈算法得到攻击者博弈树深度为2时:左侧攻击者效用为ate和21、arc和18,则左侧攻击者最优策略和效用是ate和21;右侧攻击者最优策略和效用为ate和18。防御者博弈树深度为1时:左侧防御者最优策略和效用是dtp和-211;右侧防御者最优策略和效用是dtp和-208。攻击者博弈树高度为0时:左侧攻击者最优策略和效用是ars和21;右侧攻击者最优策略和效用是ate和18。 综上所述,智能电网安全三角模糊序贯博弈均衡路径攻击者的最优策略是ars和ate,防御者的最优策略是dtp;基于贝叶斯序贯博弈最优策略攻击者是ars和ate,防御者是dtp。引入三角模糊序贯博弈对智能电网进行攻防判定和攻防效用,使得均衡路径和最优策略优于贝叶斯序贯博弈。 本文针对智能电网中的工艺流程、工艺参数等脆弱性引起的物理生产装置、对象损毁等现象,将三角模糊数理论引入序贯博弈分析模型,解决了难以用精确数值表示攻防双方损益值的问题,为智能电网攻防策略提供了决策分析方法。首先,本文通过序贯博弈模型研究了SD、攻击者成本、防御者成本以及攻防效用。其次,本文通过三角模糊数形式和概率分布为网络攻防博弈SD的判定奠定了基础。试验结果表明,智能电网序贯博弈和均衡路径获得了攻防双方最优攻击策略和最优防御策略,对实际电网安全防护具有一定的指导意义。2 三角模糊数序贯博弈算法
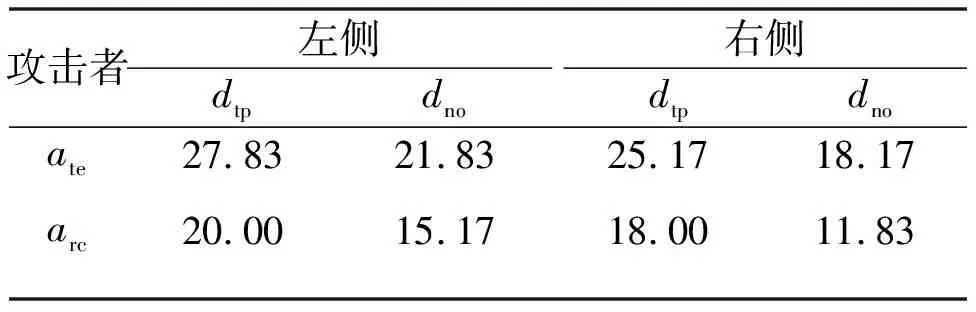
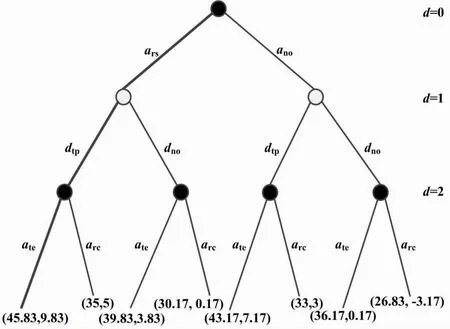
3 工控安全三角模糊数序贯博弈仿真




4 结论

