混合策略改进鲸鱼优化算法在圆柱度误差评定中的应用

吕星辰，郑鹏，程亚红，郑嘉琦

(1.郑州大学机械与动力工程学院，河南郑州 450000；2.郑州大学国际学院，河南郑州 450000)

0 前言

随着现代制造业的高速发展，精密轴类零件成为机械产品的重要组成部分。因为它往往需要配合起来使用，因此不仅要满足尺寸精度要求，同时还要满足形位精度要求。其中圆柱度误差是衡量这类零件形状误差大小的主要指标，它也直接影响到零件的工作精度和系统的寿命。因此如何能够快速、准确、高效地实现圆柱度测量和评定就显得尤为重要。

在新一代产品几何技术规范(GPS)中，根据理想要素拟合方法的不同，圆柱度误差评定方法主要分为最小二乘法(Least Square Cylinder，LSC)、最大内接柱法(Maximum Inscribed Cylinder，MIC)、最大外接柱法(Minimum Circumscribed Cylinder，MCC)和最小区域法(Minimum Zone Cylinder，MZC)。在众多评定方法中[1]，最小二乘法较为简单快捷，但只是近似评定，在生产活动中容易造成误判；而最小区域法是研究热点，因其符合最小条件准则，所以通常在误差评定发生争议时起到仲裁作用[1]。

对于圆柱度误差及其优化算法，国内外众多学者已经进行了深入的研究。王瑞[2]建立了圆柱度误差评定的线性规划模型，该模型将非线性模型线性化，方便求解，但因略去高阶项而存在模型误差。温文炯、温英明[3]采用Newton法及Gauss消去法求解非线性方程组来评定圆柱度误差，并通过实验对比最小二乘法，证明该算法过程简便实用，结果具有唯一性。郭慧等人[4]将改进的遗传算法应用于圆柱度误差的评定中，引入多种群的迁移策略有效提高全局搜索能力，通过实验对比了各个模型的精度，验证了其可行性。史栩屹等[5]设计了一种二次插值鲸鱼优化算法，通过与其他优化算法对比，验证了其具有较快的收敛速度和较好的精度。综上，这些先进的优化算法均可以对圆柱体进行全局尺寸评定，但其收敛速度及稳定性依然有待提高。

根据座头鲸围捕猎物的行为，MIRJALILI、LEWIS[6]提出了鲸鱼优化算法，其原理通俗易懂，参数设置较少，但算法容易陷入局部最优，收敛速度较慢。本文作者提出一种混合策略改进的鲸鱼优化算法，进一步提高算法的收敛速度和精度。

1 圆柱度误差评定模型

对于圆柱度误差的评定，通常采用截面法，即确定提取窗口在圆柱轴向的起止范围后，对窗口内多个平行横截面上沿周向进行采样[7]，然后通过求解不同截面上各测点的径向偏差值来反映圆柱零件在该截面处相对于理想要素的变动量，进而得到圆柱度误差。

1.1 数学模型的建立

如图1所示，首先，建立Oxyz空间坐标系，设圆柱零件的回转轴为z轴，评定基准轴线为理想圆柱轴线L。然后，沿z轴方向等距截取若干个平面，各个截面沿周向等距采样，其坐标表示为Pij(Rij，θij，zi)，理想轴线L与xOy平面交点为O1(x，y，0)，它相对于z轴的倾斜角为γ，分别用γx和γy来表示倾斜角在xOz、yOz平面上的投影分量。

图1 圆柱度几何模型

则各测点相对于理想轴线的坐标可以表示为

(1)

那么各测点到轴线L的距离可以表示为

(2)

将上式进行泰勒展开，略去高阶项，可简化为

rij=Rij+(x+αzi)cosθij+(y+βzi)sinθij

(3)

其中：α=tanγx，β=tanγy。

1.2 圆柱度误差的包容评定

包容评定分为双包容和单包容(包括外包容和内包容)。以双包容为例，即被测实际要素被两同轴的理想圆柱面包容，当两理想圆柱面径向偏差达到最小时，差值f就是圆柱度误差。因此通过前述公式可知，不断寻找最优理想轴线L的位置，使各测点均落在由max(rij)和min(rij)构成的理想圆柱曲面内，且要保证其差值最小化，便可得到圆柱度误差值[8]。

双包容评定模型为

Fmin(x，y，α，β)=min(max(rij)-min(rij))

(4)

外包容评定模型为

Fmin(x，y，α，β)=min(max(rij))

(5)

内包容评定模型为

Fmin(x，y，α，β)=min(-min(rij))

(6)

2 混合策略改进鲸鱼优化算法

在自然界中，座头鲸通常以群居为主。在捕食过程中，首先鲸群会将猎物团团包围，然后通过螺旋上升并吐出气泡的方式来收缩包围圈，直到捕食成功。根据这种行为，鲸鱼优化算法将捕食过程分为包围收缩、螺旋上升和随机游动3个搜索机制。

对于传统的鲸鱼优化算法，为了解决其容易陷入局部最优解和收敛速度相对较慢的问题，以及增强其全局搜索能力，将算法在种群初始化阶段引入Tent混沌映射来优化初始种群质量；在包围收缩阶段引入非线性参数来加速收敛；在螺旋上升阶段引入自适应权重系数提高算法局部搜索能力；在随机游动阶段引入莱维飞行提高算法全局搜索能力。其详细介绍在以下小节中进行展示[9-11]。

2.1 种群初始化

设算法的搜索空间为d维，种群中有n只鲸鱼个体，最大迭代次数为T，变量的上下限分别为ub和lb，则第t次迭代中第i只个体表示为Xi(t)=(xi，1，xi，2，…，xi，d)，则鲸鱼优化算法通过随机数来生成初始种群，如下式：

X=(ub-lb)·rand(0，1)+lb

(7)

(8)

其中：ε=0.7。且要避免初值xn与参数ε相等，否则就不再是混沌系统，将会演化为周期系统。那么式(7)将改进为

X=(ub-lb)·f(xn)+lb

(9)

2.2 包围收缩

包围收缩搜索机制是鲸鱼种群向着最优个体Xbest(t)游动来更新位置。公式如下：

(10)

其中：a为线性因子，随着迭代次数从2线性减小到0，且系数向量A在该阶段的模小于1。但为了加快收敛速度，避免陷入局部最优，在此将上述线性因子改为非线性的，使其前期变化迅速，而后期变化缓慢，从而达到目的。公式如下：

(11)

2.3 螺旋上升

螺旋上升搜索机制是鲸鱼种群通过螺旋游动来更新其位置并通过吐出气泡的方式来收紧猎物的移动空间。该阶段位置更新方式如下：

(12)

其中：b为决定螺旋形状的参数，通常取1；l为[-1，1]间的随机数。

随着迭代次数的增加，气泡网会逐渐缩小，容易使算法陷入局部最优解中。为了使全部猎物均被收缩在包围圈内，加入一个权重w，自适应地去更改鲸鱼收紧猎物的移动范围，达到当w较小时缩小包围范围、w较大时扩大包围范围的效果。

w=rand(0.5，1)+ft/fg

(13)

其中：fg为当前全局最优适应度；ft为第t次迭代中的局部最优适应度。因为w取值在[1，2]的范围内概率更大，所以大概率会选择扩大收缩包围圈，从而较好地解决了陷入局部最优的问题。其位置更新公式由式(12)变化为

X(t+1)=Xbest(t)+D2·ebl·cos(2πl)·w

(14)

2.4 随机游动

随机游动搜索机制是当前鲸鱼个体Xi向着当前鲸鱼种群中一个随机个体Xrand(t)靠近来更新位置。虽然可能会偏离目标猎物，但是能够增强全局搜索能力。该阶段，系数向量|A|>1，位置更新模型如下：

一到冬天，要检查几次。不是怕别的，怕老鼠打了洞。葡萄窖里很暖和，老鼠爱往这里面钻。它倒是暖和了，咱们的葡萄可就受了冷啦！

(15)

为了进一步增强算法的全局优化能力，引入了莱维飞行，其搜索步长的概率分布是有重尾分布的随机行走，即具有大概率出现较大跨步的情况。其飞行步长s为

(16)

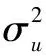
(17)

其中：Γ(x)为Gamma函数。因此改进后的位置更新公式为

(18)

其中：sign函数能取-1、0、1这3个值，代表着方向；常数ζ=0.01。

3 实验与分析

3.1 实验准备

此次实验主要运用MATLAB强大的运算功能对采集的数据进行数据分析，并将结果可视化。数据的采集仪器为三坐标测量仪，如图2所示。

图2 运用三坐标测量仪对零件进行数据采集

实验前对圆柱零件轴向等距采集10个截面，每个截面周向等距采集1 164个数据点。通过编程实现圆柱度的最小二乘评定(LSC)和双包容评定(MZC)。为了测试混合策略改进的鲸鱼优化算法(HWOA)在圆柱度误差评定上的性能，设置对照组，除了鲸鱼优化算法以外，再加入遗传算法(GA)进行对比。

3.2 实验步骤

以双包容评定为例，给出改进鲸鱼优化算法圆柱度误差评定的步骤，其简化流程如图3所示。

图3 算法流程

步骤1，给定算法的相关参数，设置算法的搜索空间为d=8，种群数量为n=100，最大迭代次数为T=500，变量的上下限ub、lb区间为[-30，30]。

步骤 2，利用式(9)生成初始种群，其中xn=rand(n，d)，再用式(4)计算初始种群中每个鲸鱼个体的适应度值，并进行比较，得到初始最优个体Xbest(0)和初始最优适应度值。

步骤 3，开始迭代并更新鲸鱼位置。在每一次迭代前首先更新参数p、a、A、C、l、w的值。判断概率p和参数|A|的值，若p<0.5且|A|<1，则采用包围收缩的方式更新种群位置，否则采用随机游动的方式更新位置；若p≥0.5，则采用螺旋上升的方式更新位置。

步骤 4，再由式(4)计算更新位置后的鲸鱼个体的适应度，并保存最优个体Xbest(t)和局部最优适应度。并判断是否达到最大迭代次数，否则继续迭代。

3.3 函数测试实验

如表1所示，为了评估改进后算法相对于原始算法的性能，选择2个可变维的基准函数来进行测试，包括一个单峰基准函数评估算法收敛速度和一个多峰基准函数评估算法全局搜索能力，且所有基准函数均有理论最优值(全局最小值)。

表1 基准测试函数

设定两算法的种群规模和迭代次数保持一致，分别为100和500，算法维度设置3个档次来进行对比，分别为50、100、200。对于每个基准函数，两优化算法均独立运行10次，计算结果的平均值和标准差，如表2所示，算法收敛曲线对比如图4所示。

表2 不同维度下HWOA与WOA算法性能对比

图4 不同维度下HWOA与WOA算法收敛曲线对比

在单峰函数中，由图4(a)可以看出改进的算法具有较快的收敛速度，并且在求解Sphere函数时精度能比原始算法高出10个数量级。在多峰函数中，由图4(b)可以看出，两种算法精度相对变化不大，但改进的鲸鱼优化相对于原始算法的收敛速度提升更加明显，展现出其具有更强的跳出局部最优的能力。综合来看，基于混合策略改进的鲸鱼优化算法(HWOA)具有更快的收敛速度和全局搜索能力。综合对比图4中所有收敛曲线，可以看出在对基准函数不同维度的求解过程中，其收敛曲线波动范围不大，展现出算法的稳定性。

3.4 实验结果对比分析

基于双包容评定，各优化算法对圆柱度误差f的评定结果对比如表3所示。

表3 各算法双包容评定结果对比

混合策略改进鲸鱼优化算法评估结果及两算法收敛速度对比如图5—6所示。其中图6为了使变化趋势更加明显，对y轴坐标进行取对数运算。

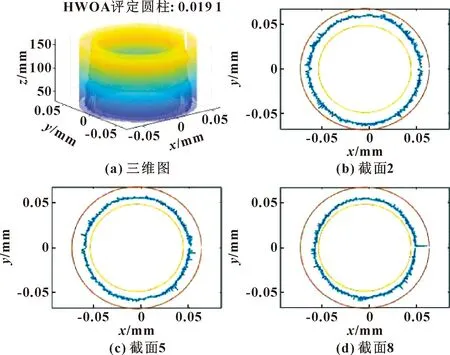
图5 改进鲸鱼优化算法评定结果

图6 算法收敛速度曲线对比

分析表3可知：基于混合策略改进的鲸鱼优化算法相对于传统鲸鱼算法在评定精度上有了进一步提升。由图6可以看出：改进的鲸鱼优化算法在第36次迭代时收敛，遗传算法在第89次迭代时收敛，而鲸鱼优化算法在第124次迭代时收敛，收敛速度提升较大；改进的鲸鱼优化算法在算法迭代初期变化速度较快，后期变化速度较慢，说明非线性因子有效改善了算法的收敛效果。

为了对比算法的效率，在固定截面数的前提下，对不同算法引入时间函数，计算其运行时间，每个算法单独运行5次取平均值，对比结果如表4所示。

表4 不同算法运行时间对比

分析表4可知：WOA算法改进前后运算时间基本无差别，因此改进算法引入的各个参数并不会增加算法的复杂度而影响运算时间；但改进后的算法相对于遗传算法在运行效率上具有较大的优势；最小二乘法运算效率最高，但该方法只是近似评定，不满足最小条件准则，因此仅供参考。

表3中误差数据为指定高度等间距采集10个截面所测得的结果。为了测试截面数量对误差值的影响(以双包容为例)，设定采样高度在30～165 mm之间，同样为等间距取样，分别间隔60、45、30 mm，得到3、4、5个截面数下的误差值如表5所示。

对比表3和表5数据可以发现：HWOA、WOA、GA、LSC运算出来的结果伴随着截面的变化具有略微的波动，但影响不是特别大，且具有略微上升的现象。这是因为随着采样截面不断增加，其采样结果越来越逼近真实圆柱零件，使得圆柱度误差越来越接近真实值。由各算法间对比可以看出：改进后的鲸鱼优化算法，在精度上具有一定的优势，不同截面数下的误差值均相对较小。

为验证在单包容评定中是否也会出现这种趋势(以MCC为例)，同样设定采样高度在30～165 mm之间，采样间隔为60、45、30、15 mm，得到3、4、5、10个截面数下的误差值如表6所示。

表6中各算法评定结果随着截面数的变化曲线与最小二乘(LSC)算法的变化曲线如图7所示。

从图7可以看出：在单包容评定下也同样具有略微上升的趋势，且各自的变化波动也较小。

4 结论

在鲸鱼优化算法的基础上引入Tent混沌映射、非线性参数、自适应权重系数和莱维飞行，来改进鲸鱼优化算法的不足。通过基准函数测试，证明基于混合策略改进的鲸鱼优化算法具有更快的收敛速度，算法的搜索能力也有了提高。经过实验对比，相比基于GA、WOA算法的圆柱度误差评定方法，改进后的鲸鱼优化算法在精度上优于其他3种对比方法，评定效率也具有显著优势。

基于混合策略改进的鲸鱼优化算法，原理简单明了，算法编程也不复杂，局部以及全局搜索能力有了进一步提升，应用场景也比较广泛，可以推广至多种问题的求解中。