考虑混凝土强度随机不均匀分布的重力坝动力损伤研究
马天骁,张燎军,沈德建,王伟强
(1. 沈阳农业大学 水利学院,辽宁 沈阳 110866; 2. 河海大学 水利水电学院,江苏 南京 210098;3. 河海大学 土木与交通学院,江苏 南京 210098)
0 引言
在我国西南高地震烈度区建有大量的高坝,其中混凝土坝占有相当大的比例。在地震过程中,大坝抗震薄弱部位的混凝土很容易发生局部损伤、开裂,甚至产生贯穿性裂缝;基岩中存在的微裂隙也可能进一步地扩大、张开,严重影响大坝的抗震安全。为了真实地模拟地震过程中大坝和基岩的破坏过程,必须考虑坝体和基岩材料的非线性力学行为。经过长期研究,基于混凝土塑性损伤理论来计算分析混凝土坝在地震过程中的损伤开裂已经成为研究大坝抗震安全非常重要的手段之一。如LEE等[1]基于LUBLINER提出的塑性损伤模型,建立了能够考虑混凝土拉压损伤及拉压相互转化的损伤模型,并被大型有限元分析软件ABAQUS采用。很多学者采用塑性-损伤耦合模型,分析了重力坝、拱坝在超强地震荷载作用下的损伤开裂[2-7]。此外,张我华等[8]提出了能够考虑岩石类脆性材料的损伤破坏模型。李静等[9]、陈健云等[10]采用混凝土塑性损伤模型研究了强震下高拱坝的承载能力。这些研究表明,混凝土塑性损伤模型可以很好地模拟地震过程中大坝的损伤破坏。
值得注意的是,混凝土是一种由骨料和砂浆等组成的复合材料,在微观层面上分布有很多毛细孔隙和结晶等。混凝土并不是一种均质材料,这是它的固有特性。对于大坝混凝土而言,在实际的施工过程中,受施工周期和季节气温的影响,同一强度等级的混凝土由于天气因素的不同,导致混凝土的凝结速度和水化过程存在一定的差异性。所以在分仓浇筑时,各仓混凝土浇筑质量很难达到绝对的相同[11]。因此,对于重力坝、拱坝所采用的大体积混凝土来说,它的固有特性、浇筑时的施工质量以及在大坝运行过程中出现的老化劣化等原因共同导致了大坝混凝土强度的不均匀性。然而,在目前的混凝土坝抗震分析中,一般将混凝土看成是一种强度均匀分布的材料。即便在计算中考虑了坝体的材料分区,在同一强度等级的分区内仍然认为它的强度是均匀分布的,关于混凝土强度随机不均匀分布对大坝和基岩整体动力损伤影响研究还比较少。
鉴于此,本文以Koyna重力坝为例,基于Weibull概率分布模型和混凝土塑性损伤模型,采用Python语言对ABAQUS进行二次开发,在考虑混凝土塑性损伤的前提下,进一步研究其强度的随机不均匀分布对大坝动力损伤的影响规律,建立了坝体混凝土的强度随机不均匀分布模型。采用有限元非线性动力分析,从震后坝体—基岩整体损伤区域分布、坝体损伤面积比和损伤耗能等角度进行对比分析,得到坝体混凝土强度随机不均匀分布对重力坝动力损伤的影响规律。
1 混凝土强度参数随机分布理论
1.1 混凝土塑性损伤参数
本文采用的混凝土损伤参数是基于ABAQUS中的混凝土塑性损伤模型(CDP模型),采用能量等效原理计算得到的。基于能量损失方法的混凝土损伤变量定义为[12]
(1)
(2)
(3)
式中:Wε为材料损伤时的应变能密度;W0为材料未损伤时的应变能密度。当混凝土未损伤时,Wε=W0,此时损伤因子D=0;在混凝土损伤的极限状态时Wε远小于W0,此时损伤因子D→1。
在混凝土本构方程σ=f(ε)上划分n个相等的小区间,对于每一小区间分别以一条抛物线代替原来的f(ε),表达式为[12]
(4)
1.2 基于Weibull概率模型的混凝土损伤参数
在采用有限元法对结构进行离散时,一般认为单个单元内部的材料特性是均匀连续的,但不同单元的力学性质是可以存在差异的,即可以表现出离散性和不均匀性。对于混凝土坝来说,当坝体划分的单元足够多时,可将每一个单元作为一个样本点,样本单元的材料特性可以认为服从某个概率分布模型,坝体所有单元构成一个总体。用这种方法虽然不能反映每个单元内部材料的细观差异,但当样本点足够多时,也可以在一定程度上体现大坝混凝土的细观不均匀性。根据相关学者的研究,如钟红[11]建议采用Weibull分布对岩石、混凝土材料非均匀性进行模拟。鉴于此,本文采用Weibull概率分布模型来考虑混凝土力学性能的不均匀性。Weibull概率密度函数定义为[13]
(5)
式中:u为混凝土的力学特性,如弹性模量或抗拉、抗压强度等;u0为相应的平均值;m为定义概率密度函数的形状,是反映材料均匀程度的指数,m值越大表示材质越均匀。
基于式(4)、式(5)可计算混凝土参数,由于坝体混凝土单元通常数目较多,靠人工将每一个单元都按照Weibull概率分布模型随机赋予混凝土损伤参数工作量过于庞大。为此,本文采用Python语言对非线性有限元程序ABAQUS进行二次开发,将生成的混凝土力学参数随机分配到每个坝体单元中,完成混凝土不均匀分布模型的建立。
2 计算模型及参数
2.1 有限元计算模型
印度Koyna重力坝坝高103 m,库水位91.75 m。该坝在1967年经受了6.3级地震,震后大坝下游面的折坡处出现了不同程度的裂缝,这是目前为数不多的遭受过强震破坏并且有完整地震记录的实例,很多学者都采用该坝作为研究对象。本小节建立的坝体和基岩的有限元分析模型如图1所示,坝体和基岩采用平面四节点单元,共划分单元数17390个,其中坝体单元4218个。
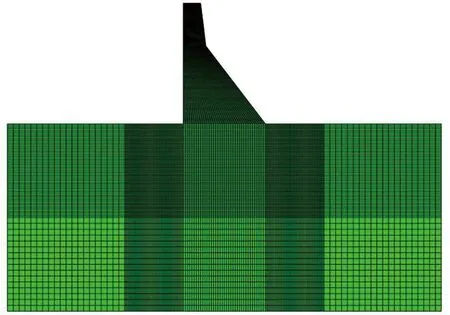
图1 Koyna重力坝坝体和基岩有限元分析模型Fig.1 Finite element analysis model of dam body and bedrock of Koyna gravity dam
坝体混凝土材料参数为:弹性模量E0=30 GPa ,泊松比μ=0.2,密度ρ=2630 kg/m3,抗拉强度ft0=2.9 MPa,抗压强度fc=24.1 MPa。在进行高坝抗震分析时,地基岩体的损伤破坏是坝体、地基和库水体系的损伤破坏分析中不可忽视的重要因素。基岩作为多裂隙随机分布的非均匀介质,其损伤应与混凝土类似。但由于无法对岩体进行力学试验,目前只能借鉴混凝土的损伤演化规律[14]。为了体现基岩在地震过程中的损伤、开裂行为,考虑到基岩和混凝土都是准脆性材料,具有相似的力学性质,本文根据文献[14-16]的建议,将基岩的材料参数按照式(6)折算为混凝土的强度参数,其表达式为
(6)
经过折算后,基岩的抗拉强度为1.2 MPa,弹性模量E0=20 GPa,泊松比μ=0.2,密度ρ=2700 kg/m3。
计算荷载包括坝体自重、静水压力、动水压力和地震荷载。动水压力采用Westergarrd附加质量方法进行模拟,采用Rayleigh阻尼,阻尼比为5%。分别输入实测的顺河向和竖向地震波,时程曲线如图2所示。采用黏弹性边界[17-19]来模拟基岩的辐射阻尼效应,通过波动输入法以等效节点力[20]的形式实现地震动输入。
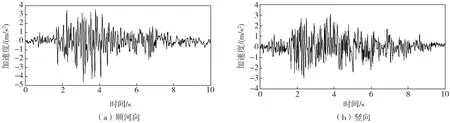
图2 Koyna地震波Fig.2 Koyna seismic waves
2.2 基于Weibull概率分布的坝体损伤参数
为了研究混凝土强度不均匀分布对重力坝动力损伤的影响,本小节采用Weibull概率分布函数来反映材料的非均匀性。分别考虑当不均匀指数m为3、5、10、15时重力坝的动力损伤情况,m值越大混凝土越均匀。将采用Weibull概率分布模型计算的混凝土参数随机分配到坝体各个单元中,使每个单元的材料参数都各不相同,但总体上满足Weibull概率分布模型。具体操作细节是:如当给定的m为3时,因本模型坝体单元数目为4218个,按照Weibull分布模型生成4218个样本的混凝土材料参数,这4218个样本整体上服从m为3的Weibull分布,然后将这4218个样本随机分配到坝体各个单元中。重复上述过程,即得到m为5、10、15时的不均匀模型。
对于特定的m值,在生成了相应的4218个样本混凝土参数后,要把这些参数分配到坝体各个单元中,但这种分配具有随机性,为了排除偶然因素,全面反映各个不均匀指数下坝体的动力损伤情况,本文对每个不均匀指数都采用5个样本进行计算。即对于每一个m值,都进行了5次随机分配,尽可能避免随机偶然因素的影响。
受篇幅限制,本文只列出各个不均匀指数下的一组样本的参数统计结果,其他样本统计结果与此类似。由于混凝土抗压强度较高,在重力坝动力分析中常常只考虑受拉损伤,因此本文仅列出抗拉强度的统计图,如图3所示。图中ft0为混凝土设计强度下抗拉强度的标准值,ft为各个单元实际的抗拉强度值。采用比值的形式来统计坝体混凝土强度参数的离散情况,由图3可知,m值越小,离散程度越大,随着m值的增大,统计数据越来越向标准值集中,离散性逐渐降低。
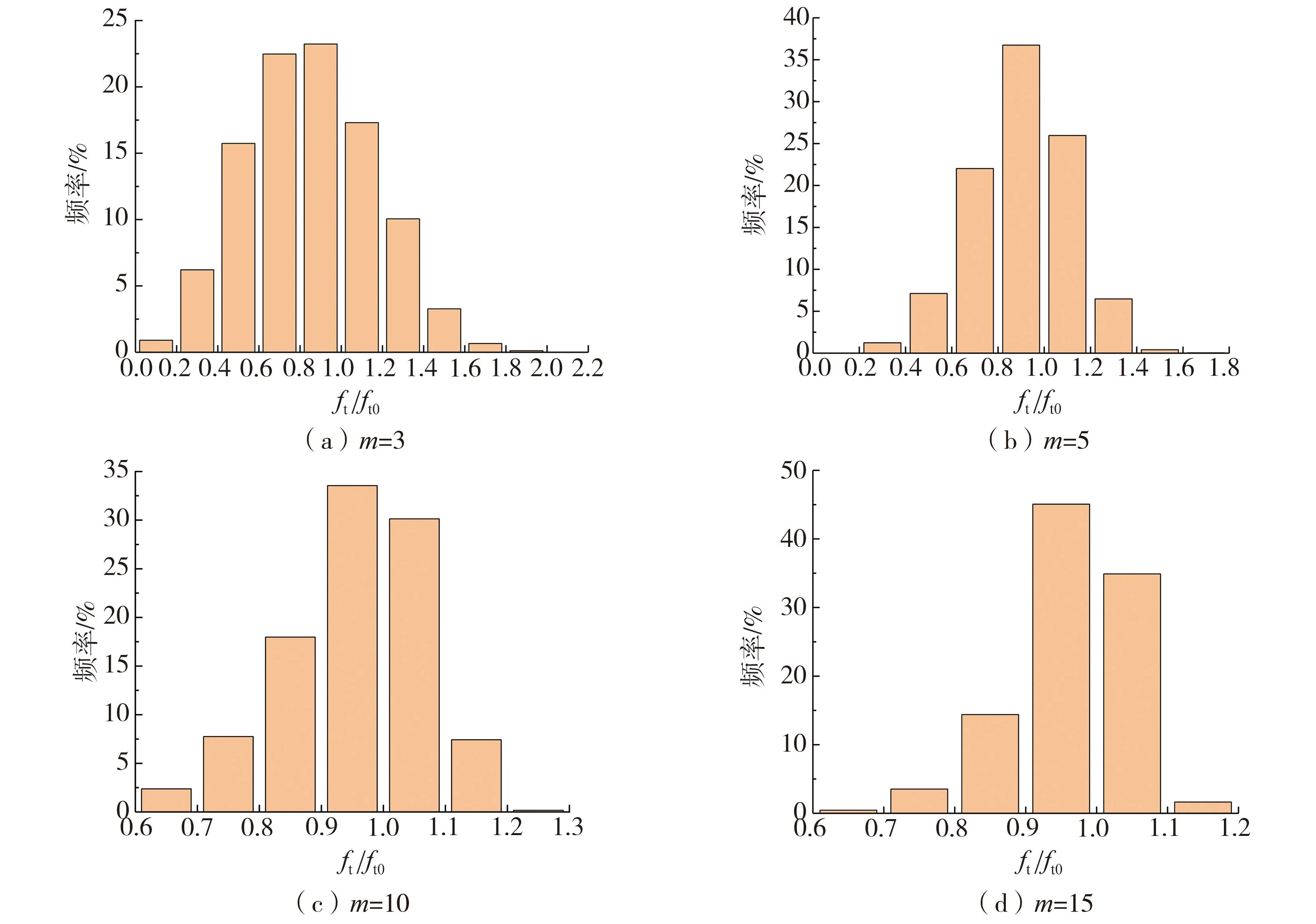
图3 各个不均匀指数下抗拉强度分布Fig.3 Distribution of tensile strength under each heterogeneity index
3 震后坝体和基岩损伤分析
3.1 坝体和基岩损伤区域分析
首先计算当坝体混凝土均匀分布时坝体和基岩的损伤情况。震后大坝下游折坡处出现了一条向上游面扩展的损伤区域,上游坝面也出现了轻微的损伤区,这与Koyna重力坝实际震害的坝体损伤开裂模式相同,如图4所示。由于基岩的抗拉强度远比混凝土小,所以地震时往往基岩首先沿着坝踵向下开裂,这使得坝踵附近的拉应力得到释放,故坝踵在地震中没有损伤,这也与实际震害情况一致。该算例与实际震害结果的对比表明:本文所采用的材料模型、地震动输入方法、远域地基辐射阻尼的模拟、坝体与库水的动力相互作用等非线性动力分析方法是合理的。
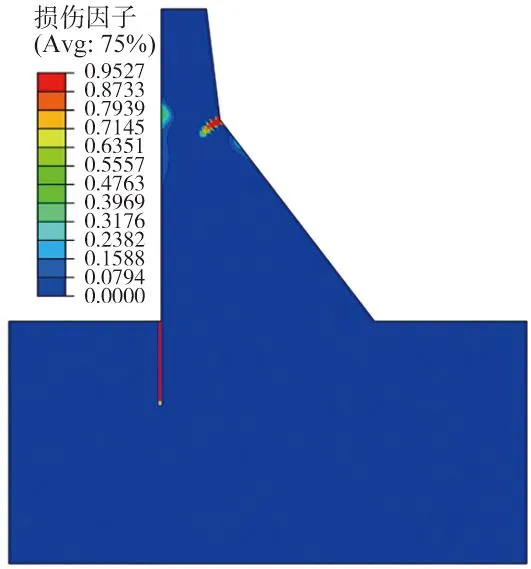
图4 混凝土均匀分布时坝体和基岩损伤分布Fig.4 Dam and bedrock damage distribution when concrete is uniformly distributed
当材料的不均匀指数m为3时,坝体混凝土的材料参数离散性较大,为了全面地反映该不均匀指数下坝体和基岩的损伤情况,采用5个样本进行计算。这5个样本中,坝体每个单元的材料参数都是随机分布、各不相同的,但总体上都服从m为3时的Weibull分布模型。由图5可知,当m为3时,坝体折坡处附近的上下游面均出现大量的损伤单元,处于红色的严重损伤单元从上下游面向坝体内扩展、交汇,损伤区域和严重程度明显比图4中均匀分布时更大。对于坝体中下部,尽管材料也不均匀分布,但并未有大面积的损伤。这说明重力坝的抗震薄弱部位在坝体上部的折坡处附近,该处混凝土的施工质量对大坝的抗震性能尤为重要,且浇筑质量不均匀时会比均匀浇筑的损伤程度更大、危害更为严重。从图中还可以发现,5个样本的损伤分布情况非常相近,破坏模式相同,这说明服从同一Weibull分布的模型,计算结果离散性较小。此外,从基岩损伤的角度分析,5个样本的基岩损伤区域和坝体均匀分布相比,均未发现明显的区别,这表明坝体混凝土强度的不均匀分布对于基岩的损伤影响不大。
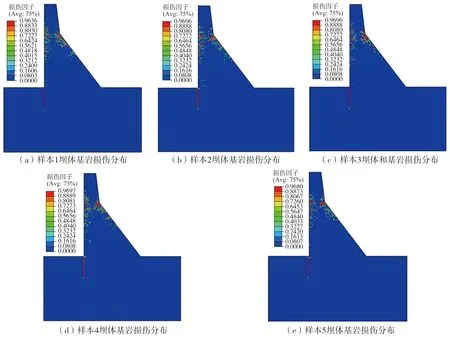
图5 当m=3时各样本坝体和基岩损伤分布Fig.5 Damage distribution of dam and bedrock of each sample when m=3
当材料的不均匀指数m为5时,坝体单元总体上都服从m为5时的Weibull概率分布模型。坝体的损伤程度比m为3时稍有减轻,损伤单元的数目和范围都有所减少,但仍可以看到处于红色的严重损伤单元从上下游面向坝体内扩展、交汇,损伤区域和严重程度还是明显比图4均匀分布时更大。基岩损伤区域和坝体均匀分布相比,均未发现明显的区别,如图6(a)所示。当材料的不均匀指数m为10时,坝体的损伤程度比m为5时更为减轻,损伤单元的数目和范围都有所减少,如图6(b)所示。当材料的不均匀指数m为15时,坝体的损伤程度和均匀分布时较为接近,但上下游面仍有小部分单元处于损伤状态,如图6(c)所示。
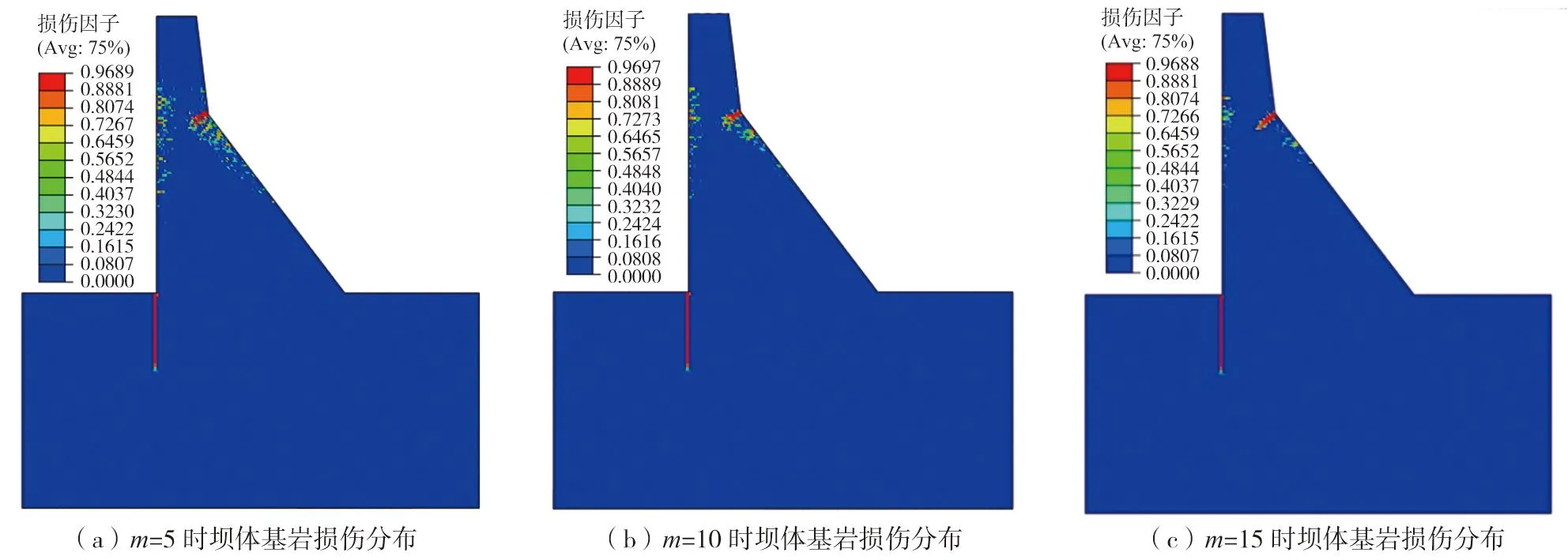
图6 各个m值下坝体和基岩损伤分布Fig.6 Damage distribution of dam body and bedrock under each m values
3.2 坝体损伤定量分析
为了更为准确客观地反映坝体和基岩的损伤情况,本节通过采用损伤耗散能和损伤面积比2个指标来定量的研究不同均匀程度的坝体的损伤规律。
由于在大坝地震损伤的过程中常常伴随着损伤耗能的增加,因此损伤耗能指标可以在一定程度上反映坝体裂缝发展情况[21],损伤耗能采用式(7)计算,得
(7)
式中:MD为坝体损伤耗能;σ为坝体单元应力;εck为开裂应变;V为单元体积,对于二维模型指单元面积。
采用式(7)分别计算均匀分布及m为3、5、10、15时,5组样本的坝体震后损伤耗能,并绘制出损伤耗能随地震时间的变化曲线,如图7所示。从5组样本的损伤耗能曲线可以看出,随着地震动的持续,坝体损伤耗散能逐渐增大。一般来说,坝体进入损伤状态的单元数目越多,损伤程度越严重,坝体的损伤耗散能越大。由于地震动峰值加速度出现在第三秒附近,坝体的主要损伤破坏区域在此阶段已经形成,故损伤耗散能会发生明显增加。随后的时间虽然地震动在持续,但强度逐渐衰减,坝体损伤范围仅在原有的基础上小范围的增加,未出现新的大面积的损伤区域,故整体耗散能也有增量,但不会如第三秒附近的耗散能一样,发生明显的增量。坝体混凝土分布越均匀(m值越大),震后坝体损伤耗散能越小,混凝土分布离散性越大(m值越小),震后坝体损伤耗散能越大。从定量的角度进一步表明坝体混凝土强度的不均匀分布对大坝抗震能力影响较大,不均匀性越大,对大坝的抗震安全越不利。
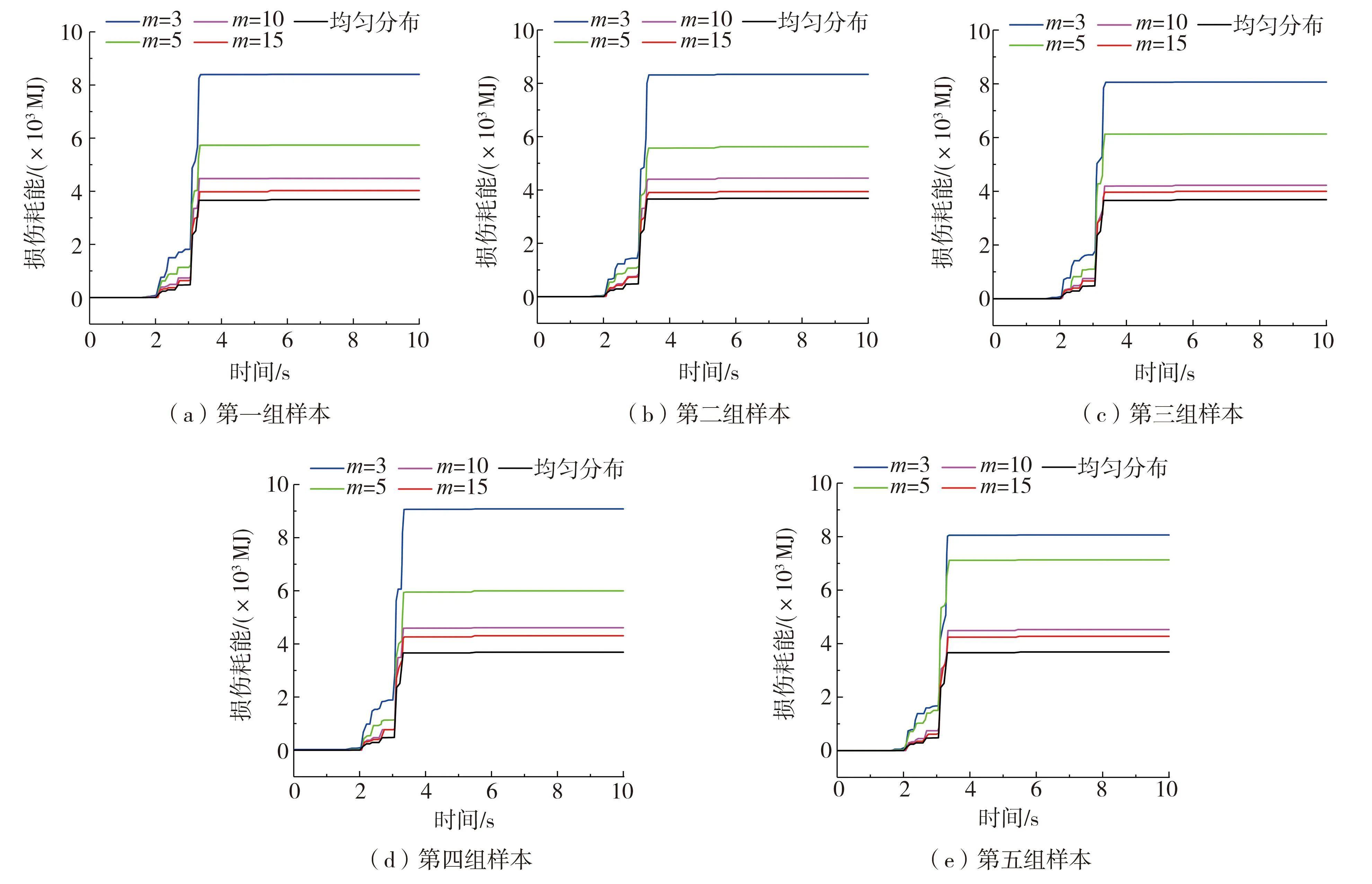
图7 各组样本坝体损伤耗散能曲线Fig.7 Dam damage dissipation energy curves of samples in each group
除了坝体损伤耗能指标外,坝体损伤面积比(damage area ration, DAR)也是反映大坝在地震过程中损伤状况的重要定量指标,损伤面积比定义为
(8)
式中:n为坝体单元数目;i为坝体单元编号;di(t)为i号单元在t时刻对应的损伤因子;Ai为i号单元的面积。损伤面积比的范围为0~1,损伤面积比越大,表示坝体损伤情况越严重。当损伤面积比为0时,表示坝体无损伤,当损伤面积比为1时,表示坝体所有单元已完全损伤。
采用式(8)分别计算在各个不均匀指数下各样本坝体震后损伤面积比并进行汇总,如图8所示。由图可知,坝体损伤面积比随着m值的增加而减小,m值越大即材料分布越均匀,损伤面积比数值越接近完全均匀工况下的计算结果。同时也可以看出,相同m值下的5个样本得到的损伤面积比数值非常接近,分布在平均值附近,离散性很小。这从定量的角度说明了在样本总体服从同一Weibull概率分布模型的情况下,计算结果差异较小。
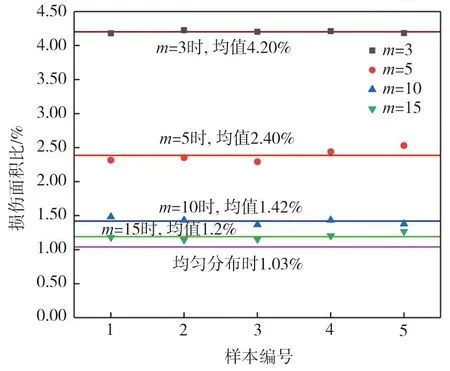
图8 各组样本坝体损伤面积比Fig.8 Dam damage area ratio of samples in each group
需要说明的是:本文将m值分别选为3、5、10、15来进行分析,主要是为了更好地对比研究混凝土坝在各个不均匀度下坝体的震后损伤破坏规律,进而得到一般规律。选择m为3和5是为了分析混凝土不均匀度对坝体损伤影响规律的一种“假设”。在实际工程中,不太可能发生m为3和5这种如此程度不均匀分布的情况,实际Koyna坝的震损也未发生如m为3和5的严重程度。
4 结论
本文主要研究了坝体混凝土强度随机不均匀分布对重力坝动力损伤的影响,分别从损伤区域分布和损伤面积比和损伤耗能等角度分析了坝体不同程度的不均匀性对大坝损伤的影响规律,得到以下结论:
1)坝体混凝土强度随机不均匀分布对大坝抗震薄弱部位的抗震安全影响较大。对于重力坝而言,尽管在计算时整个坝体单元都考虑了强度不均匀分布,但坝体的不同区域对于混凝土不均匀程度的“敏感程度”不同。震后损伤区域仍然集中在坝体抗震薄弱部位,即上下游面折坡处附近,该区域内进入损伤状态的单元数目及损伤程度较均匀分布时明显增大。强度不均匀分布对于大坝内部的损伤则影响不大。这表明混凝土强度不均匀分布对于大坝薄弱部位的抗震性能有重要影响,在重力坝地震安全评价时,应该考虑混凝土强度分布不均匀所造成的影响,尤其要注意提高抗震薄弱部位混凝土强度的均匀性。
2)在各个不均匀指数m下,基岩的损伤情况与坝体均匀分布相比未见有明显变化,这表明坝体混凝土材料的不均匀分布对基岩的损伤区域分布影响较小。

