程潮铁矿崩落法开采对上覆岩体变形的影响研究

李吉民 吴文博 张聪瑞 陈诚 韩亚民

（1.武汉理工大学资源与环境工程学院，湖北武汉 430070；2.武钢资源集团程潮矿业有限公司，湖北鄂州 436051；3.关键非金属矿产资源绿色利用教育部重点实验室，湖北武汉 430074）

0 引言

程潮铁矿采用无底柱分段崩落法开采已深至地下-500 m 以下分段，长期的崩落法开采至今已造成了约41.7 万m2的地表塌陷，同时大范围的地表塌陷也为地表向井下汇水提供了天然通道，导致采场雨季突水、突泥的事故时有发生。对于地表塌陷而言，塌陷坑的形成与许多因素密切相关，由崩落法开采引起上覆围岩中裂隙的产生及岩体变形是直接原因，岩体中原生节理裂隙发育情况、岩体本身物理力学性质、地应力、开采深度、地下水渗流等其他因素是间接原因。探究无底柱分段崩落法开采对空区上覆围岩受力变化特征与变形破坏机制对有效控制地表塌陷、预防采场涌水具有重要意义［1-2］。

关于采矿引起的岩体稳定性分析及变形破坏机制方面，已有许多前人研究成果。张波等［3］运用3DEC数值模拟软件，结合工程实际情况针对高瓦斯煤层开采过程中的岩体裂隙带移动变形与裂隙带动态演化规律进行了模拟研究，探讨了煤层开采过程中采动覆岩裂隙与渗透演化规律的特征。夏开宗等［4］通过对矿区的地表变形监测资料及宏观破坏特征分析，对金属矿山崩落法开采引起的岩层移动规律进行了研究，并将矿区岩层随开采发生移动变化分为顶板破坏扩展、周边围岩倾倒破坏的两阶段，其研究结果从宏观上解释了金属矿山无底柱分段崩落法开采造成的上覆岩体移动及失稳过程，但仍缺乏具体单一或多矿房开采对周边围岩的应力及应变变化分析。孟庆彬等［5］应用地质雷达技术，对和睦山铁矿开挖采矿进路阶段进行了围岩松动圈探测，确定了其松动圈具体范围，并结合数值模拟分析了无底柱分段崩落法采场进路围岩变形破坏特征与失稳机理，对采场进路支护技术提供了一定的参考，但矿房开采后的围岩松动情况则由于其安全性原因导致难以使用雷达设备进行探测。刘志高等［6］采用UDEC 数值模拟和综放开采条件下覆岩移动计算的“上三带”理论相结合，对腾达煤矿覆岩运移规律开展了研究，确定了其“上三带”高度，并通过现场钻孔监测数据进行了验证，对于煤矿综放开采所造成的覆岩移动范围进行了较好的阐释。程健维等［7］以预测地表沉陷的影响函数法为基础，通过改进相关参数和理论推导，将其用于对开采导致岩层移动及变形的计算与预测，建立分段煤层工作面开采沉陷预计模型，实践表明该模型具有良好的实用性。

以上文献虽然对矿山开采地表及深部岩体的变形规律取得了诸多有益的成果，但在目前深部开采背景下，对不同分段矿房开采的上覆岩体变形规律仍不清晰，且由于金属矿山具有矿体形态多变、开采参数多变以及结构效应明显等特点，造成了由地下采矿引起的地表变形和岩体破坏形式与煤矿等沉积类地层矿山不同，针对金属矿山地下开采引起的采空区上覆岩体应力演化机制目前尚未形成系统的、全面的、可供参考的理论。因此，对采用无底柱分段崩落法深部开采的矿山，其崩落法开采对上覆岩体应力扰动与变形机制亟待于更深入的研究。

1 工程背景

程潮铁矿矿区地形为低山丘陵地貌，东西长约2 300 m，南北宽约800 m。其地下分为东、西区，采用无底柱分段崩落法进行开采，西区目前正在进行-463.0 m 分段的开采，东区主要正在进行-480 m和-500.0 m 分段的开采。同时矿山正在进行-560 m分段的提前开拓工程，-500 m 至-560 m 间矿体未开采，目前日产矿石量共计约为1×104t。

1.1 地应力场

矿区在成矿前后经历多次强烈的构造运动，形成了较为复杂的构造应力场。图1 为程潮铁矿矿区最大主应力1、最小主应力3和垂直应力2的分布规律，其中，最大主压应力1方向为N85°～75°W，与矿体走向基本一致，其大小与深度相关，在不同深度时取不同倍数的h；中间主应力2的函数关系为2=·h，与深度线性相关；最小主应力3的方向基本垂直矿体走向。

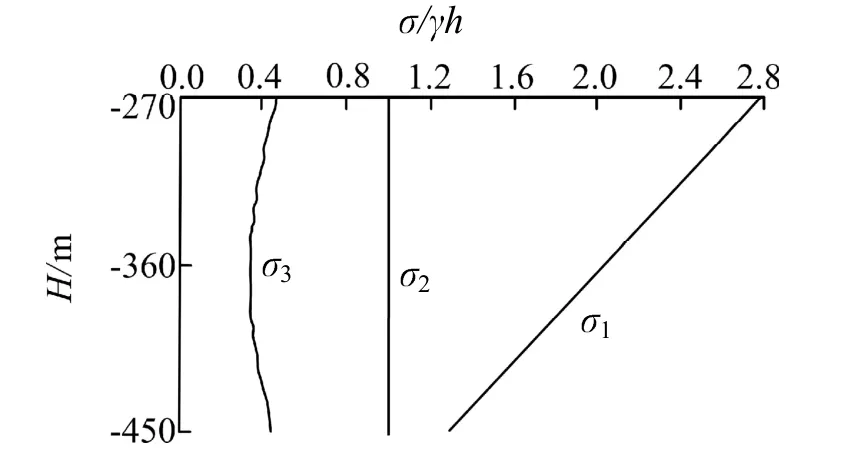
图1 程潮铁矿主应力分布示意

程潮铁矿矿区最大主应力1在-450 m 深度为1.33h，具体测量值为15.33 MPa，由此可得=0.025 7，后续将依据此对-480 m、-500 m 分段各方向应力进行计算。

程潮铁矿井下开采以70 m 划分1 个中段，中段间又划分数个分段，分段高度为17.5 m，进路间距为15 m。

1.2 模型岩石力学参数确定

矿区岩石大体可分为角岩、闪长岩、大理岩以及磁铁矿这几类。为取得UDEC 数值模拟所需的所有力学参数，包括质量密度，kg/m3；体积模量K和剪切模量G；粘聚力C、内摩擦角、抗拉强度b等。整理目前可查的地质资料，得出程潮矿区岩石物理力学性质如表1 示。

表1 矿区岩体力学参数表

2 UDEC 无底柱分段崩落法开采模拟

通用离散元程序（UDEC，Universal Distinct Element Code）是一个处理不连续介质的二维离散元程序，尤其适用于模拟非连续介质（如岩体中的节理裂隙等）承受静载或动载作用下的力学响应过程。选用UDEC 模拟程潮铁矿无底柱分段崩落法采矿过程，基于离散元理论分析各开采步骤下的围岩应力及位移分布状态，探究采矿对采空区上覆岩体稳定性的影响，为后续矿山支护及防水方案设计提供参考。

2.1 模拟方案确定

程潮铁矿自-290 m 水平到- 460 m 水平的矿体均进行了开采，但由于矿体一方面呈倾斜产状分布，因此在不同的二维剖面空区上覆围岩完整性会存在较大差异；另一方面，崩落法采矿形成的崩落空区围岩体物理力学性质难监测、难获取。因此结合研究目的，本次模拟方案设计简化为截取程潮铁矿井下的-480 m 分段、-500 m 分段与-517.5 m 分段的部分矿房，以其目前正在开挖的-480 m 分段、-500 m 分段为具体研究对象，分段上覆围岩视为未开采的完整岩体，并施加一个上边界荷载以等效上覆岩体自重应力，此种模拟工况亦与目前正在进行开拓工程的-560 m 分段情况相似。

模型大小长度取240 m（仅代表横向的尺度标记线长度），高度取200 m（两中段间距为70 m，两分段间距为17.5 m），这样的二维模型可以保证模型边界离开挖边界的距离为开挖跨度的5 倍左右，以消除模型对边界可能产生的影响。同时为方便建模和计算，模型材质仅选取角岩和铁矿石的物理力学参数，矿体部分使用铁矿石的岩石力学参数，矿体外围的部分则采用角岩的岩体力学参数，模拟开采方案为中深孔瞬时同步爆破开挖。

2.2 开挖模拟过程

2.2.1 平面模型构建

模型允许最小转角半径设置为0.3 m，最小块体边长为0.6 m，生成模型面。由于UDEC 中删除块体必须给定块体范围，且块体范围需要在预设的节理范围内，因此通过block cut crack 命令依照程潮铁矿无底柱分段崩落法开采矿房的参数布置好进路及矿房的范围节理，模型的y轴零点分段线处模拟的标高为-470 m，设计-480 m 分段开采5 个矿房，-500 m分段开采4 个矿房，进路尺寸为3 m×3 m，进路间距为15 m，矿房高度取18 m。使用UDEC 7.0 自动网格划分，为提高计算精度，将开采矩形区域的网格生成边长设置为2.0m，外部矩形的网格生成边长为5.0 m，网格划分完成后的模型图如图2 所示。

图2 模型块体与分区

2.2.2 模型岩石力学参数及边界条件

模拟中岩石本构模型设置为摩尔-库伦模型，在岩石物理力学参数设定上，开采区矿体参照表1 中磁铁矿性质，密度值取2.68×103kg/m3，体积模量取16.46×109Pa，剪切模量取6.1×109Pa，内摩擦角为30.1°，岩体内聚力6.7×105Pa，抗拉强度为4.2×105Pa；外围区岩体参照表1 中角岩性质，密度值取2.72×103kg/m3，体积模量取33.3×109Pa，剪切模量取9.4×109Pa，内摩擦角为26.8°，岩体内聚力5.3×105Pa，抗拉强度为5.6×105Pa。

岩体中节理的本构模型设置为库伦-滑移模型，节理切向刚度取值为1.0×109Pa，节理法向刚度取值为16.0×109Pa，内摩擦角为43°，粘聚力为1.0×104Pa［8］。

应力边界条件参照图1 可知，y轴零点分段线处即井下-470 m分段处，其分段方向最大分段主应力 1为1.23h，代入，h值可算出1为14.86 MPa，垂直方向第二主应力2为h，其值为12.08 MPa，最小主应力3约为0.42h，其值为5.1 MPa。因此对模型左右边界的设定约束为xx=-14.86 MPa，yy=-12.08 MPa，且均在y方向上以0.03 MPa/m 的梯度下降。

模型上边界的模拟标高为-370 m，参照前文中的地应力测量结果，-370m处的垂直地应力h=9.5 MPa，故对模型上边界整体施加随深度方向以30 kPa/m的梯度增加的9.5 MPa 的垂直地应力荷载。

最后固定模型左右及下边界的速度边界，设置引力值-9.81 N/kg，模型解算精度为1.0 E-5，开始平衡计算。计算结果的应力、位移云图如图3、图4所示。

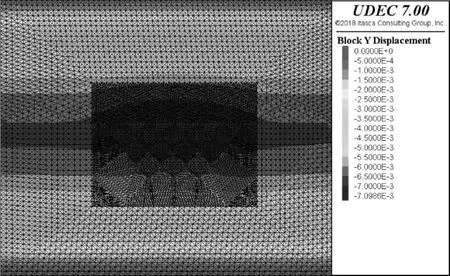
图3 块体位移

图4 块体应力

当模型进行平衡演化后，模型在y方向上应力为对称均匀分布，且呈梯度增强的受压状态，模型中轴线上的压应力自上往下由9.45 MPa 逐渐增大到14.85 MPa。模型在y方向上的位移虽然都表现为向下略微沉降，但这种沉降并不均匀，且以开挖区为核心，沉降的深度最深，达到了0.7 cm，远离核心的地方则沉降的稍少一点，初步判断可能是由于提前布置的开挖区节理力学性质弱于围岩体力学性质，由此造成沉降略微增加。

2.2.3 -480 m 分段矿房开采过程分析

模拟-480 m 分段的5 个矿房开采过程，研究周边岩体损伤及裂隙生成-扩展情况。首先开挖-480 m分段的进路，得到y方向上的位移、应力云图如图5所示。

图5 -480 m 进路开挖y 方向上的位移及应力

图中可以看出，开挖-480 m分段的进路并未对整体的位移和应力分布造成明显影响，开挖进路上方岩体y方向上的位移沉降值自0.7 cm 增至0.98 cm，即开挖5 条进路（3×3 m）对上方的矿岩造成了0.22 cm的沉降，开挖进路下方的岩体y方向上的位移自0.69 cm 变化至0.78 cm。而在应力方面，各进路在分段和竖直方向上均受压应力，但分段方向上的压应力相较于未开挖前的12～13 MPa增大至14～15 MPa，而竖直方向上的压应力表现规律为离进路顶板越远而越大，直接顶板处的压应力最小，仅为1.4 MPa；底板的受力状况与顶板近似。可以说明，进路的开挖引起了两帮围岩的应力增大，顶底板处的应力减小，位移变化上呈现出顶底板与边帮都有向里收缩的趋势，但现阶段这样的应力集中并不足以对巷道变形产生明显影响。

接下来开挖矿房，开采顺序为从左到右开采，并对每步骤开采平衡后的最大主应力云图、总计应变增量云图进行展示（见图6），其中，增量应变是指递进变形过程中各个小阶段在已发生的有限应变基础上新增的应变。需要特别说明的是，UDEC 中无法展示未提前预设节理岩体的破碎，也就是说，如果未预先在岩体中设置节理，那么这块岩体在模拟结果图中是不会发生破碎、垮落等现象的，即便其内部显示的沉降位移值等其他参数已能清楚证明该岩体内部必然发生了破碎与崩落。

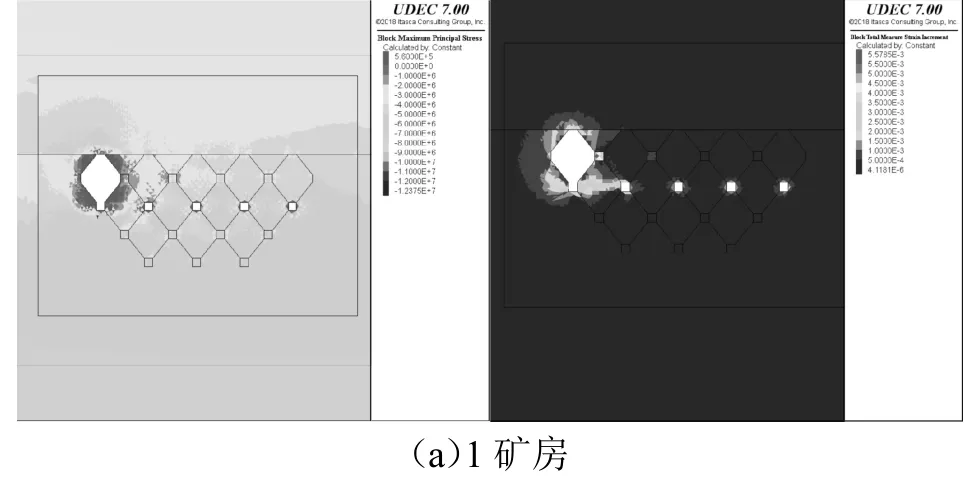
图6 -480 m分段矿房顺序回采各步骤最大主应力、总计应变增量

最大主应力云图中将图例的拉应力最大值取为定值0.56 MPa，总计应变增量云图的图例显示最大值设为0.01，在不影响应力及应变的情况下优化云图显示效果，消除计算结果中少数极值带来的影响。由图7 变化过程可有：①自左向右开采矿房过程中，围岩中逐步形成应力拱和应变拱，它们的范围均随着开采逐渐扩大，且这两者在形态以及发展趋势上都高度对应；②应力拱在不同拱高内的最大主应力值存在明显的区间性，越往外越接近原始地层的最大主应力；③结合应变云图应变拱的变化情况，每开挖一个矿房所形成的分区矿柱，其承载的载荷是上一个矿柱所承载上部拱形围岩的扇形外扩围岩体，这也与岩体开挖的“自然平衡拱”［9］理论互相映证。

图7 -500 m分段矿房顺序回采各步骤最大主应力、总计应变增量

此外，每步骤矿房开采后形成的最大主应力拱相比原应力拱，其范围大小并非均匀扩张，其内部最大主应力呈现既有压应力部分，也存在拉应力部分，拉应力集中分布在应力拱下方，压应力则集中分布在上部，应力分布情况较为复杂。为更清晰地分析矿房每步骤开采对上覆岩体应力、应变变化的影响规律，并尝试性的量化这个过程，将云图中每步骤开采后上覆围岩的最大主应力拱、应变增量拱内部具体数值变化情况统计总结如表2、表3。

表2 各步骤开采围岩最大主应力情况

表3 各步骤开采围岩应变增量拱情况

结合表2 分析最大主应力的应力拱，除1 矿房开采外，其余步骤的应力拱，内部均存在拉应力和压应力占主导的两个部分，拱内拉应力和压应力的分布虽然互有交叉，但仍表现为拉应力集中分布在下部，压应力集中分布在上。而同时出现拉、压应力的原因则可以根据“三带”理论进行解释，拉应力基本也呈拱状分布于距空区最近的顶板围岩内，数值较小，拱内围岩即为开采矿房形成的冒落带，此处的顶板围岩并非不受压应力作用，只是其最大主应力已经以拉应力为主导，呈现出向下冒落的趋势，因此判断其为冒落带范围；压应力则是呈拱状向外扩散递增分布，数值越来越大，且随着范围的扩增，其数值从和原始地层应力相差较大到慢慢贴近原始地层应力值，这表明此拱内部围岩的应力状态已和外部相对脱离，由岩体内部生成大量裂隙导致应力无法有效传递，因此判断其为导水裂隙带范围。

拉应力在1步骤矿房开采后，拉应力拱尚未产生，说明此时顶板无冒落范围，后续矿房开采所致的冒落带范围高度依次为0.52、2.77、3.00、6.25 m，这些数值的变化趋势虽为不断增大，但并未见明显的数学规律。另外，除1 步骤矿房开采外，其余压应力拱的区间最大值基本保持一致，该平衡值近似为2.92 MPa。这表明，在同一分段矿房的开采过程中，每次矿房开采后，新形成的压应力拱与之前相比，除了拱径扩大外，其应力平衡状态并未发生改变。

每步骤矿房开采后应变拱拱高和表2 中的压应力分布区间的最大值在数值上都较为接近，进一步验证了前文导水裂隙带的推论。这里取表3 中的对应高度值（3.9、12.8、21.1、31.4、42.3 m）作为矿房每步骤开采后的导水裂隙带高度。由UDEC 模拟结果可知，沉降拱的高度和范围是随采长的不断增加而增大的，每增加1 个矿房（15 m）的采长，其冒落带和导水裂隙带范围均显著增加，且导水裂隙带高度范围随采长的演变趋势具有明显线性关系。

最终得到导水裂隙带高度函数可取y=0.636x-6.32，此时R2为0.995 7。此即为程潮铁矿采用无底柱分段崩落法开采，当进行单分段矿房开挖且该矿房上覆围岩未经开采时，其上覆岩体形成的导水裂隙带高度范围y随采长x的变化函数。

2.2.4 -500 m 分段矿房开采过程分析

实际崩落法采矿过程中的开采顺序为自上而下，层层崩落采矿，因此探究上下相邻分段间矿房回采对围岩产生的重复扰动影响具有重要意义。接下来对-500 m 水平矿房进行顺序回采模拟，并将其最大主应力云图和总计应变增量云图展示如图7 所示。

由于篇幅所限及-500 m分段2、3 矿房开采对应力及应变的扰动程度不明显的原因，这里只展示开采1 矿房和开采4 矿房结束后的应力及应变云图情况。图7 中可观察得出，在开采-500 m 分段矿房后，-480 m中段的矿体向下垮落，矿体下方围岩的应力及应变拱开始显现，且变化趋势与上覆围岩近似对称发展，同时，在-500 m 分段矿房的开采过程中，上覆岩体的应力拱和沉降拱的大小范围及平衡状态没有再发生明显变化，4 矿房开采结束后，测得空区上覆围岩体的最大应变拱高为42.6 m，外圈的应力拱平衡值为2.99 MPa，均与-480 m 矿房开采结束时的状态相差无几。另外，矿房边帮围岩的应力和应变范围进一步增大，往内收缩变形的趋势也更明显。

分析-500 m 分段的模拟结果，由矿房开采所形成的围岩松动圈和应力应变拱范围显著受采长这一因素变化的影响，而几乎不受采高的影响。同时推断-500m分段矿房开采未对整体围岩产生明显扰动的原因是模拟中-500 m 分段开挖的矿房均已在- 480 m分段矿房开采形成的岩体松动圈内，在松动圈内的岩体，其所受压应力大幅低于松动圈外部平衡地应力，并与圈外岩体相对独立，只要后续矿房开采形成的新应力应变拱仍未超出先前的应力应变拱范围，就基本不会对外部围岩造成损伤影响。且松动圈岩体以外的围岩承受的压应力值较高，尤以左右两边帮为甚，因此采用无底柱分段崩落法开采的矿山应当特别注意最大应力应变拱的平衡状态及范围大小，并在应力应变拱形成的圈外围岩和左右边帮围岩加强支护。

3 结论

（1）在无底柱分段崩落法开采矿体过程中，空区上覆岩体会逐步形成应力拱和应变拱，且其范围均随开采逐渐扩大，同时在形态以及发展趋势上都高度对应；应力拱在不同拱高内的最大主应力值存在明显的区间性，越往外越接近原始地层的最大主应力；在同一分段矿房的开采过程中，每次矿房开采后，新形成的压应力拱与之前相比，除了拱径扩大外，其应力平衡状态并未发生改变。

（2）利用-480 m分段中5 个矿房开采形成的导水裂隙带高度模拟结果（3.9、12.8、21.1、31.4、42.3 m）进行了线性函数拟合。得出程潮铁矿采用无底柱分段崩落法开采，当进行单分段矿房开挖且该矿房上覆围岩未经开采时，其上覆岩体形成的导水裂隙带高度范围y随采长x的变化函数，此函数有助于矿山后续生产时确定空区上覆围岩移动及损伤范围。

（3）松动圈内的岩体与圈外岩体相对独立，其所受压应力是大幅低于松动圈外部平衡地应力的，只要其开采形成的应力应变拱仍未超出原先的应力应变拱范围，就基本不会对外部围岩造成损伤影响。因此采用无底柱分段崩落法开采的矿山应当特别注意最大应力应变拱的平衡状态及范围大小，并在应力应变拱形成的圈外围岩和左右边帮围岩加强支护。