新型电力系统场景下网侧规模化储能二次调频控制策略

孙娜，董海鹰*，陈薇，马虎林

（1.兰州交通大学 新能源与动力工程学院，兰州 730070； 2.中广核太阳能嘉峪关有限公司，兰州 735100）

0 引言

随着可再生能源在电力系统中的占比不断提高，尤其是风电、光伏等具有间歇性、波动性和随机性等发电特性的新能源，其高渗透率给电网的安全稳定运行与控制带来了巨大挑战［1-3］，不仅如此，随着特高压交直流电网不断并网造成的区域电网频率异常波动，同样亟须电网具备紧急频率调节控制能力。储能系统具有灵活的双向互动性能，在电网紧急控制与频率快速响应方面具有重要的应用价值［4-6］，特别是电化学储能系统因其具有响应速度快、调节精度高等显著优点［7-8］，相比于其他类型的储能系统，具有更优良的功率调节性能和频率控制能力［9-10］。

目前，储能电站主要受调度中心实现整体的运行控制，储能电站接收由调度中心下发的自动发电控制（Automatic Generation Control，AGC）指令来实现全站功率调节的分配，机组响应AGC 指令时对区域控制需求（Area Regulation Requirement，ARR）信号控制和区域控制偏差（Area Control Error，ACE）信号控制的切换策略一直是储能参与电网二次调频的研究重点。

文献［11］基于储能电池的动态调频容量（Dynamic Available AGC，DAA）对ACE 和ARR 信号分配模式全期调频效果进行分析。文献［12］中将AGC 信号划分为三类优先级不同的调节区域，并依据不同优先级对调频电源进行合理分配。文献［13］发现ACE 信号有利于快速调频前期恢复暂态频率偏差，ARR 信号则有利于恢复调频中后期的稳态频率偏差。

进一步，文献［14］在复频域提出以灵敏度过零点作为2 种信号模式切换的判据，从理论层面分析了ACE 信号分配有利于暂态偏差而ARR 信号分配有利于稳态偏差。文献［15］利用经验模态分解将AGC 信号分解成高频和低频部分，让电池储能系统（Battery Energy Storage System，BESS）承担高频分量，帮助快速恢复暂态频差，让传统机组承担低频分量，帮助恢复稳态频差，但该策略没有考虑电池荷电状态（State of Charge，SOC）的影响，容易对电池储能长期参与调频造成不可逆的损害。文献［16］考虑不同调频电源的技术特征，在多约束条件以下调频成本最小为目标进行调频责任的分配，但由于传统机组的爬坡率限制或者BESS 的SOC 限制，在后续调频的成本模型中可能会降低约束函数的求解精度进而对机组的责任分配结果产生影响。

在目前的研究中仍存在一些问题：绝大多数储能电站仅仅实现了储能电站级AGC 控制，缺乏对各独立储能单元之间协调控制的考虑，不利于储能长期投入运行；响应AGC 指令时，对ACE 和ARR 信号的分配方法也未能基于信号的调频优势进行自适应切换。

基于以上所述，本文在新型电力系统场景下提出一种考虑荷电状态的网侧规模化储能二次调频控制策略。首先，基于区域电网响应AGC 指令的动态调频模型，设计兼顾ARR信号和ACE信号特点的模糊控制器，在实现2 种信号自适应切换的同时满足电网调频需求；其次，基于2种信号的自适应切换模式，在考虑各储能单元的调频能力的同时维持SOC 水平在合理范围内，并通过模糊控制实现各储能单元的出力功率指令跟踪。最后仿真验证所提策略的有效性。

1 网侧独立储能系统调频模型

基于区域等效的方法，在网侧建立规模化储能参与二次调频的区域电网频率响应模型。其中，新型电力系统场景下的规模化储能系统并网结构图如图1 所示，区域电网频率响应模型如图2 所示［17-18］，模型中的参数定义见表1。

表1 参数定义列表Table 1 Parameters and their definitions

图1 规模化储能系统并网结构Fig.1 Structure of the large-scale grid-connected energy storage system

图2 区域电网频率响应模型Fig.2 Regional grid frequency response model

在新型电力系统场景下，新能源参与电网调频有2种方式：（1）新能源作为调频机组；（2）新能源作为负荷扰动。本文所建模型中，新能源作为负荷扰动参与调频过程，模型由调度中心和储能系统的控制单元组成，可实现一次调频和二次调频，储能电站区域内配置J个储能单元进行调频。

2 规模化储能响应AGC指令的信号分配控制

2.1 信号的分配模式管理

BESS 参与电网调频时的调频信号分配模式分为基于ARR 信号分配和基于ACE 信号分配，基于ACE 信号分配能够改善系统的暂态频率偏差，基于ARR 信号分配能够改善系统的稳态频率偏差［17］。本文通过综合考虑2 种信号进行频率调节的特点，通过设计二阶模糊控制器实现2种信号控制的自适应切换。基于ACE 分配和基于ARR 分配的大规模储能参与电网调频的频率响应模型如图3、图4 所示。AGC（s）为AGC 指令的信号输入，贡献因子α可以确定2 种信号控制在响应AGC 指令时的贡献程度。

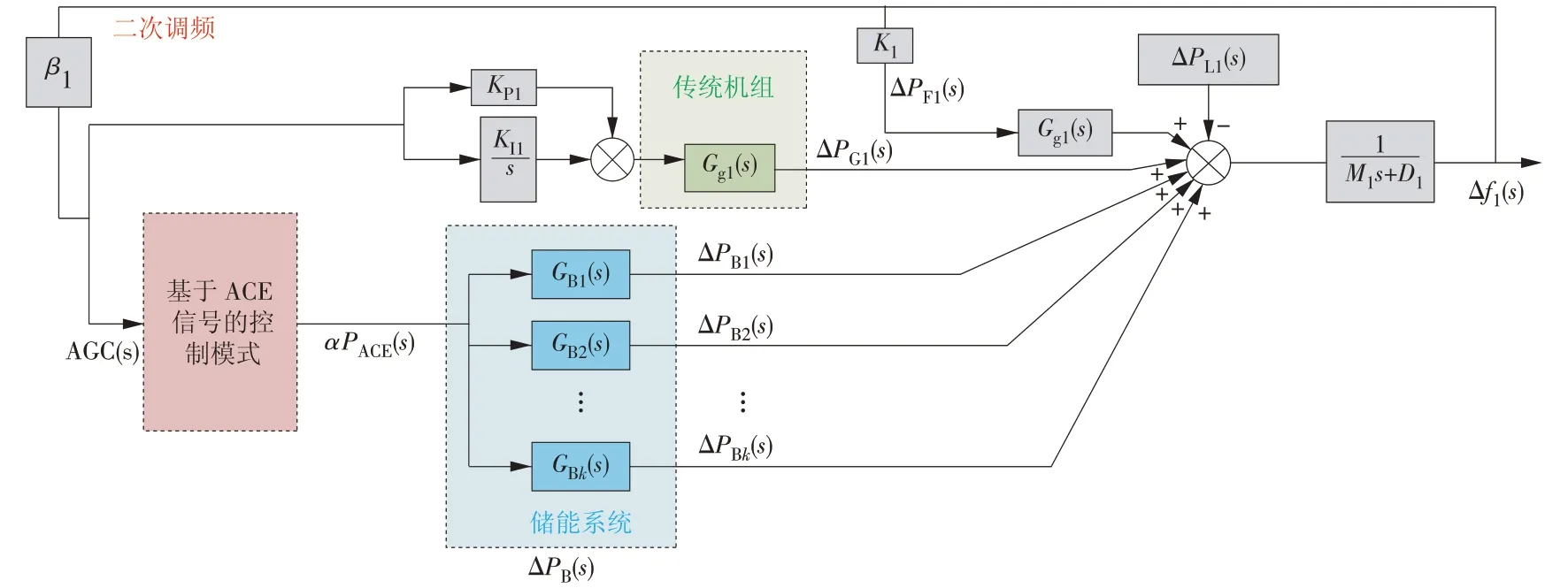
图3 基于ACE信号的频率响应模型Fig.3 Frequency response model based on ACE signal

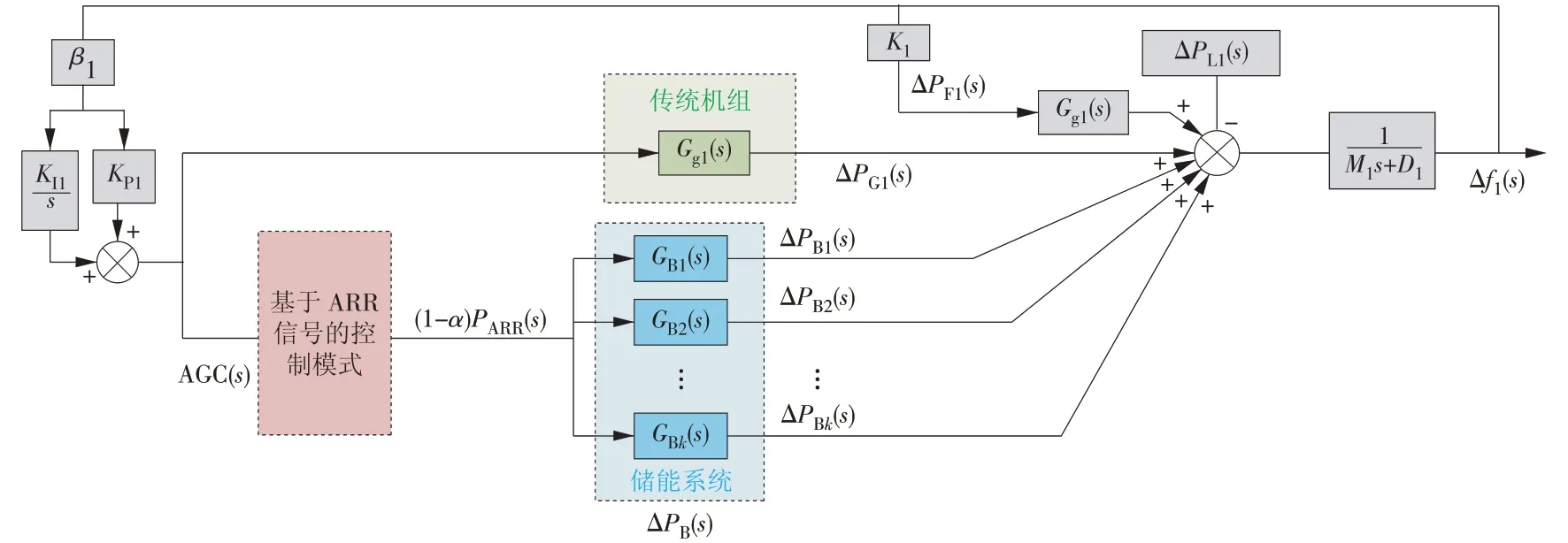
图4 基于ARR信号的频率响应模型Fig.4 Frequency response model based on ARR signal

不计调频死区和限幅约束，由图3、图4可得

式中：PACE（s）和PARR（s）为基于ACE信号和ARR 信号2 种控制方式下的功率输入。频率偏差Δf1（s）具体为

储能系统的模型为

综上所述，将式（1）—（3）代入后可得储能系统的总出力ΔPB（s）为

式中：KACE和KARR为储能响应AGC指令的控制系数。

2.2 实现双信号自适应切换的模糊控制

ACE 信号控制适合对系统暂态频率偏差进行调节，ARR 信号控制适合对系统稳态频率偏差进行调节，结合2种信号频率调节的特点，设计二阶模糊控制器实现2种信号控制的自适应切换。

模糊控制器基于电网的调频需求，设计新型电力系统场景下的频率偏差Δf1（t）和频率偏差变化率dΔf1（t）/dt作为输入量，推导2 种模式下的储能总功率响应和电网频差需求的联系，确定2 种信号控制的贡献因子α（t），从而得到储能实际出力深度。

模糊控制器为二维控制，输入量Δf1（t），dΔf1（t）/dt的比例因子和输出量α（t）的比例因子k11，k12和k13如式（5）所示

式中：Δfmax（t）为储能二次调频的最大允许区间。

隶属度函数选用Mamdani型隶属度函数。Δf1（t）和dΔf1（t）/dt为模糊控制器的两个输入，其论域范围均为［-1，1］；α（t）为模糊控制器的输出，其论域范围为［0，1］。模糊集为｛NB（负大），NO（负中），NS（负小），ZO（零），PS（正小），PO（正中），PB（正大）｝。

模糊控制器的控制规则为：当系统频率偏差频率偏差Δf1（t）和频率偏差变化率dΔf1（t）/dt较大时，储能设备应充分结合ACE 和ARR 信号控制的优势来快速调节较大偏差，储能系统响应AGC 信号的贡献因子α应该接近0.5；当系统频率偏差频率偏差Δf1（t）和频率偏差变化率dΔf1（t）/dt较小时，储能设备应减少大幅度调频动作，故应增加ACE 信号控制的贡献占比α；当系统频率偏差Δf1（t）较大且频率偏差变化率dΔf1（t）/dt较小时，应充分发挥ARR 信号控制的优势，储能系统响应AGC 指令的贡献因子α也应该随之减小；当系统频率偏差Δf1（t）较小且频率偏差变化率dΔf1（t）/dt较大时，应充分发挥ACE信号控制的优势，储能系统响应AGC 指令的贡献因子α也应该随之增大。

其次，定义Δf1（t），dΔf1（t）/dt和α（t）的隶属度函数值分别为Au1(t)，Au2(t)和Au3(t)。最终可以得到输入Au1(t)，Au2(t)和输出Au3(t)的三维关系如图5所示，模糊控制规则见表2。

表2 模糊控制规则Table 2 Fuzzy control rules

图5 输入输出三维关系1Fig.5 3D relationship between inputs and outputs 1

对Δf（1t）的输出模糊量Au3(t)使用面积重心法进行反模糊化，最终得到参与因子

式中：Au1(t)，Au2(t)分别为dΔf（1t）/dt和α（t）的输入模糊量；u1，u2分别为输入模糊量Au1(t)，Au2(t)的自变量。

3 各储能单元的均衡分配控制

均衡控制对参与调频的多组储能单元所承担的调频出力进行二次有效分配，实现了各组储能单元的协调配合，可以有效抑制个别储能单元的过充过放现象以及提前退出调频行为，对储能的SOC 水平起良好的维持作用。模糊控制器基于储能的调频能力，设计各组储能单元的初始出力和各组储能单元的SOC 水平QSOC（t）作为输入量，推导各组储能单元SOC 和出力深度的联系，确定各组储能单元在SOC 均衡控制后的的实际出力深度ΔPBj（t）。其中，各组储能单元的初始出力深度为

式中：ΔPBjmax(t)为各组储能单元二次调频最大允许出力。

模糊控制器的控制规则为：当各组储能单元的SOC 水平QSOC（t）过大或过小时，为防止储能因过充过放而受到损坏，储能单元的实际出力深度ΔPBj（t）应该适当减少；反之，储能单元的实际出力深度ΔPBj（t）应该适当增加。其次，定义，QSOC（t）和ΔPB（jt）的隶属度函数值分别为Bu1(t)，Bu2(t)和Bu3(t)。最终可以得到输入Bu1(t)，Bu2(t)和输出Bu3(t)的三维关系如图6所示，模糊控制规则见表3。

表3 模糊控制规则Table 3 Fuzzy control rules

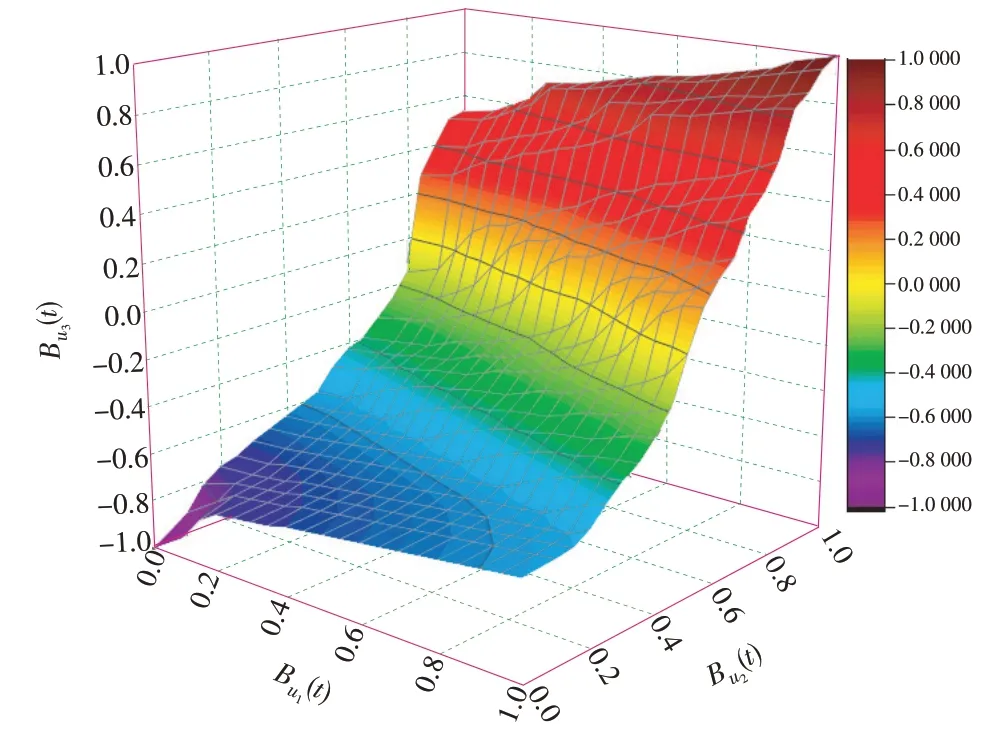
图6 输入输出三维关系2Fig.6 3D relationship between inputs and outputs 2

式中：Bu1(t)，Bu2(t)分别为QSO（Ct）和ΔPB（jt）的输入模糊量；u1和u2分别为输入模糊量Bu1(t)，Bu2(t)的自变量。

4 仿真及结果分析

4.1 仿真参数

采用图1所示的储能参与二次调频的等效模型在Matlab/Simulink 平台中搭建仿真，传统机组采用额定功率为750 MW 的再热火电机组，各储能单元的额定功率和容量见表4［18］。

表4 储能系统参数Table 4 Energy storage system parametersMW

以额定频率50 Hz 和机组最大额定容量为基准值进行标幺化。设计阶跃扰动和连续扰动2种典型工况，就本文所提出的控制策略（方案3）和传统动态调频容量控制策略（方案2）以及无储能参与（方案1）进行对比仿真，对比分析以检验所提控制策略的有效性。系统仿真参数见表5［19］。

表5 系统仿真参数Table 5 System simulation parameters

4.2 阶跃扰动

分别在第2，22 s 加入负荷扰动Pload（标幺值）为0.005 和0.010 的阶跃扰动。为了更好地根据评价体系来验证本文方法的有效性，利用3 种方案在阶跃扰动下的频率偏差、各机组出力以及各储能单元荷电状态的变化曲线来进行比较［20］。负荷扰动如图7所示。

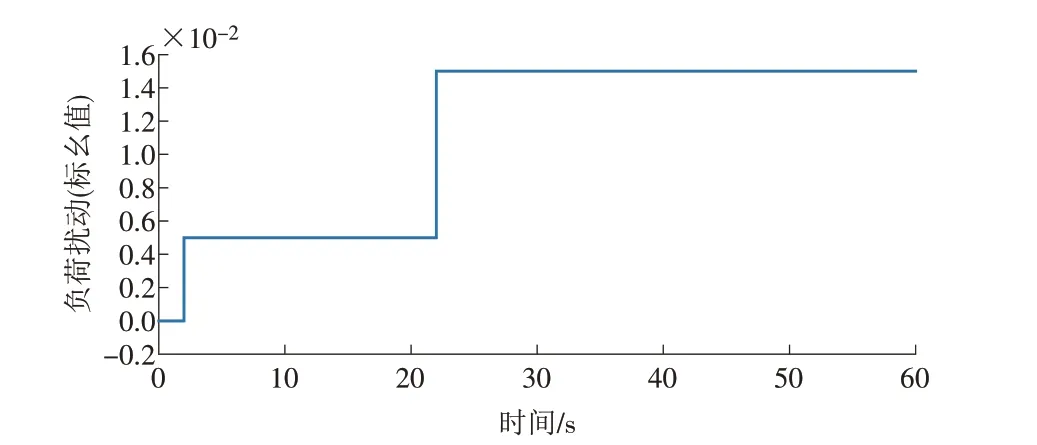
图7 负荷扰动Fig.7 Load disturbances

加入负荷扰动后系统的频率偏差变化曲线如图8所示。

图8 频率偏差Fig.8 Frequency deviations

由图8可以看出，3种方案均能够对频率偏差进行无差调节。相比较于方案1 和方案2，方案3 的频率下降速度比方案1 和方案2降低了11.49%和1.79%，且频率恢复速度比方案1 和方案2提高了19.16%和1.51%，同时在恢复的过程中能够将频率偏差的波动控制在更小的范围内。

加入负荷扰动后各调频机组的出力变化曲线如图9 所示。储能单元1 的容量大且出力多，储能单元4 的容量小且出力少，方案2 缺乏对各储能单元的出力进行均衡控制，储能单元1 由于承担过多出力受到损害，方案3 在加入均衡控制后使各储能单元的出力均衡，从而延长储能的使用寿命。

图9 各机组出力Fig.9 Output of each unit

加入负荷扰动后储能的荷电状态变化曲线如图10所示。

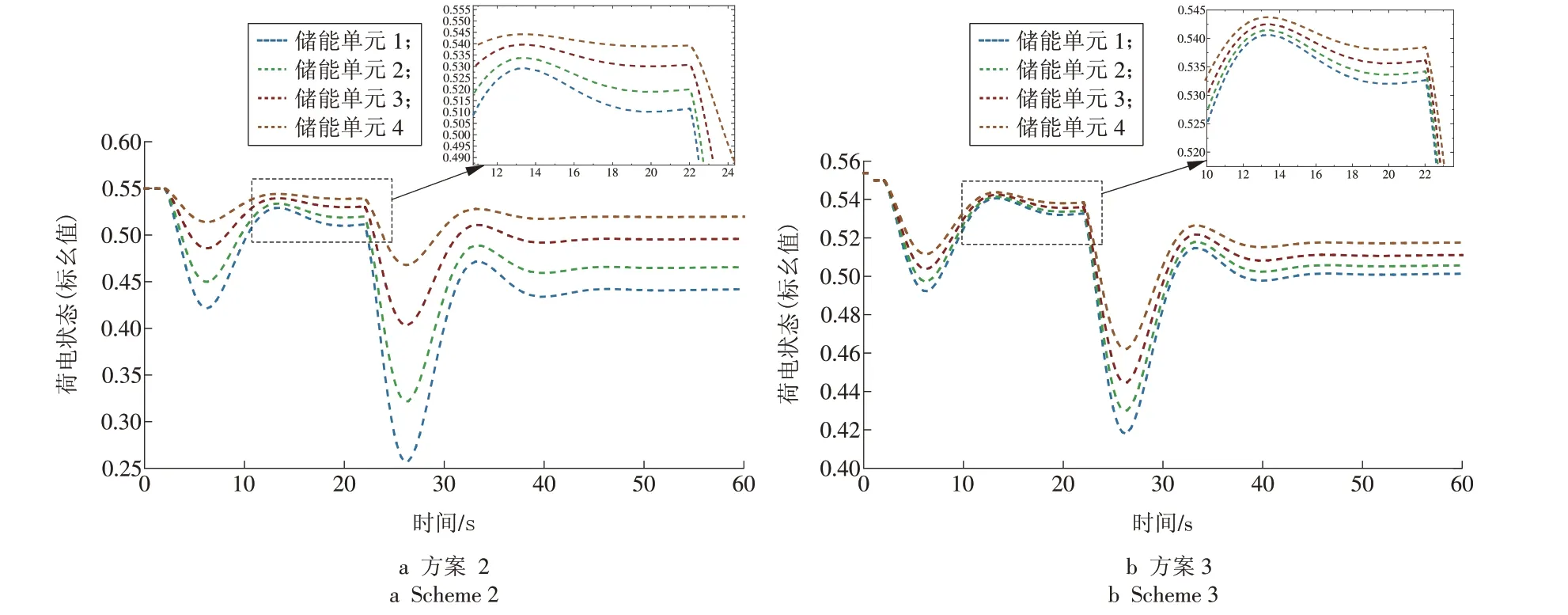
图10 各储能单元SOCFig.10 SOC of each energy storage unit

储能的初始荷电状态为0.55，调频结束后的荷电状态会逐渐恢复到初始值，相比较于方案2，方案3 中各储能单元的SOC 变化均衡且波动较小，能够将各储能单元的SOC 变化稳定在0.40～0.55，且方案3荷电状态的维持水平比方案2提高了64.7%。

4.3 连续扰动

在区域内加入如图11所示的负荷扰动Pload。为了更好地根据评价体系来验证本文方法的有效性，利用3 种方案在连续扰动下的频率偏差、各机组出力以及各储能单元荷电状态的变化曲线来进行比较。

图11 负荷扰动Fig.11 Load disturbances

加入负荷扰动后系统的频率偏差变化曲线如图12所示。

图12 频率偏差Fig.12 Frequency deviations

3 种方案均能够对频率偏差进行无差调节。相比较于方案1 和方案2，方案3 的频率下降速度比方案1 和方案2降低了7.49%和1.25%，且频率恢复速度比方案1 和方案2提高了9.16%和2.11%，在恢复的过程中也能够将频率偏差的波动控制在更小的范围内。

加入负荷扰动后各调频机组的出力变化曲线如图13所示。

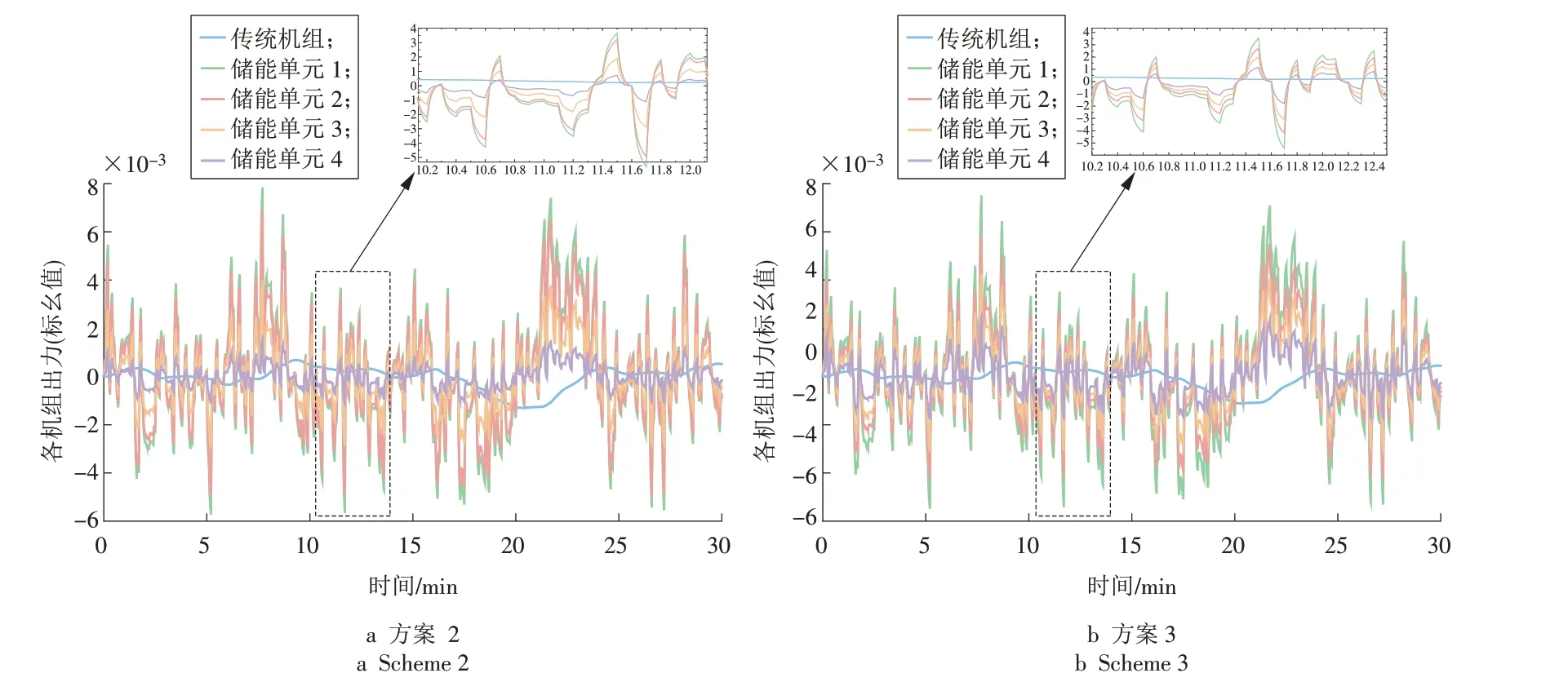
图13 各机组出力Fig.13 Output of each unit

各储能单元的容量不同造成出力严重失衡，方案2 缺乏对各储能单元的出力进行均衡控制，个别储能单元由于出力过多而长期处于过充过放状态，方案3 在加入均衡控制后使各储能单元的出力均衡，从而延长储能的使用寿命。

加入负荷扰动后储能的荷电状态变化曲线如图14所示。

图14 各储能单元SOCFig.14 SOC of each energy storage

储能的初始荷电状态为0.55，相比较于方案2，方案3 中各储能单元的SOC 变化均衡且波动较小，能够将各储能单元的SOC 变化稳定在0.40～0.55，且方案3 荷电状态的维持水平比方案2 提高了64.7%。

5 结论

本文综合考虑电网调频需求和机组调频能力，提出一种考虑荷电状态的网侧规模化储能二次调频控制策略。其优点如下：基于电网调频需求，储能在响应AGC 指令时通过模糊控制对双信号控制模式进行自适应切换，充分发挥2 种信号控制优势的同时提高储能对调频需求的匹配度；基于储能系统的调频能力，本文控制策略能够对具有不同技术特性的储能单元调频出力深度进行均衡控制，在维持各储能单元SOC 的同时避免个别储能过充过放，有效延长了储能系统的使用寿命。