考虑构网型和跟网型变流器的孤岛微电网小信号稳定性分析

张心怡，杨波

（1.德国柏林工业大学 电气工程与计算机科学学院，柏林 10587； 2.东北大学 信息科学与工程学院，沈阳 110167）

0 引言

随着可再生能源渗透率的提高以及电力电子设备的不断迭代，传统大规模、集中式的电力系统正逐步向分布式、智能化、可持续方向发展［1］。微电网作为一种高效整合分布式能源的新型电力系统，得到了广泛关注。微电网需要在并网模式和孤岛模式下稳定运行，由于孤岛微电网面临系统惯量小、无电网频率支持的问题，因此保障孤岛微电网的稳定十分有挑战性［2-4］。

分布式能源由变流器接入微电网。变流器按照工作模式一般可分为构网型变流器和跟网型变流器［5-7］。跟网型变流器是基于电压定向的电流源，依赖锁相环与电网同步，可通过直接电流控制或级联电压电流环控制实现分布式能源功率输出，但无法给系统提供电压和频率支持；构网型变流器具有电压源特性，可通过下垂控制等方法给系统提供电压和频率支持［8-11］。因此，在孤岛微电网中，至少需要一个变流器工作于构网模式［12］。在具有感性线路的网络中，变流器的输出有功功率和输出频率耦合，无功功率和输出电压耦合，因此，变流器的输出频率可通过控制输出有功功率来调节，而输出电压可通过调整无功功率得到［13］。

小信号稳定性是指系统在小干扰后保持稳定的能力，是保障孤岛微电网可靠运行的关键［14-15］。通过对工作点附近的非线性系统线性化，可得到工作点附近的小信号模型。通过特征值分析及参与因子分析等方法可对小信号模型进行稳定性分析。多数关于孤岛微电网稳定性的研究基于仅含构网型变流器的微电网，没有考虑跟网型变流器［16-18］；此外，恒功率负载（CPL）由于其负阻抗特性，对微电网的稳定性造成了挑战［19］。

本文针对含有构网型、跟网型变流器及CPL 的孤岛微电网稳定性问题，首先构建系统的小信号模型，在该模型的基础上利用特征值分析法得到能够保障系统稳定运行的下垂系数的上界；其次，通过参与因子揭示系统参数和控制参数对小信号稳定性的影响；最后，通过仿真验证小信号分析的结果以及下垂系数取值的有效性。

1 孤岛微电网结构及模型建立

1.1 孤岛微电网电路结构

该微电网由2个相同的基于构网型变流器的电池储能系统（BESS）、1 个由跟网型变流器连接的CPL及线路网络构成，如图1所示（图中：Rlinei，Llinei分别为线路i的电阻和电感）。变流器均经过LCL 滤波器在公共连接点（PCC）处并联。构网型变流器通过下垂控制策略得到其输出电压频率和幅值的参考值，并通过级联电压电流控制器得到变流器的控制信号；跟网型变流器采用电流前馈解耦控制策略，通过锁相环实现与系统频率同步，并通过级联电压电流环控制功率输入及CPL 直流母线的电压稳定；此外，系统的建模和控制均在dq轴中实施。

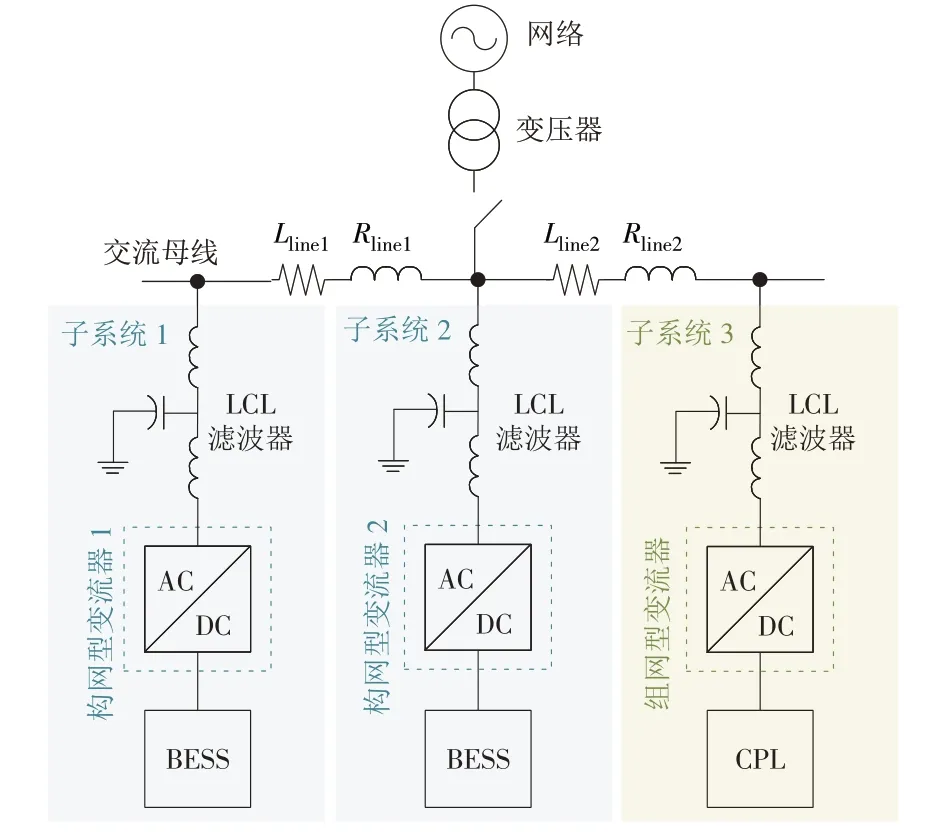
图1 孤岛微电网电路结构Fig.1 Architecture of the islanded microgrid

1.2 基于构网型变流器的子系统小信号模型

构网型变流器的控制系统由功率控制器、电压控制器、电流控制器、abc与dq轴的相互转换模块以及脉冲宽度调制（PWM）信号发生器构成，如图2 所示。由于PWM 信号发生器的高频特性，系统建模时可忽略其动态模型（图中：Lft，Cf和Lfg共同构成了LCL 滤波器分别为abc，dq轴的输出电压参考值为输出电流参考值；itabc，itdq分别为变流器在abc，dq轴中的电流；为输入电流控制器的电压在d轴的参考值；ioabc，iodq分别为变流器在abc，dq轴的输出电流；voabc，vodq分别为LCL 滤波器中滤波电容在abc，dq轴的输出电压；ω为旋转角频率）。

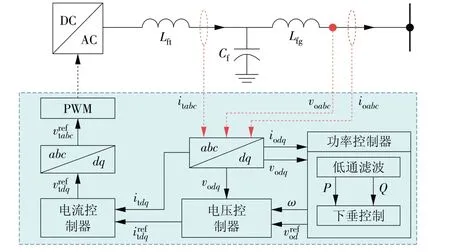
图2 构网型变流器及控制系统Fig.2 Grid-forming converter and its control system

功率控制器采用下垂控制策略得到其输出电压的参考值，其数学模型为

式中：P，Q分别为变换器的输出有功、无功功率；ωc为低通滤波器的截止角频率；θ为构网型变流器的旋转角度；ωn，Vn分别为额定旋转角频率和额定输出电压；Pn，Qn分别为额定有功、无功功率；mp，nq分别为功率控制器的有功、无功下垂系数。

将由功率控制器得到的电压参考值信号输入级联电压电流环中，该控制环的数学模型为

式中：αdq，γdq分别为电压控制器和电流控制器中PI补偿器的积分部分；为变流器在q轴的输出电压参考值，设为0；kpv，kiv分别为电压PI 控制器的比例参数和积分参数；kpc，kic分别为电流PI 控制器的比例参数和积分参数；Fi，Fv分别为电流和电压反馈系数。

该变换器交流侧在dq轴上的动态模型为

式中：vtd，vtq分别为该变流器在dq轴的输出电压；vbd，vbq分别为PCC处电压在dq轴中的值。

此外，构网型变流器的建模是在其各自生成的dq轴中进行的，在整个系统的模型中，需要将各个独立dq轴中建立的模型通过转换矩阵转换到同步参考系DQ轴中。该转换矩阵的表达式为

式中：δi为第i个变换器的dq坐标系与同步参考系的角度差。

在DQ轴中得到的某些变换器的控制量也需通过如下逆变换矩阵转换到各自dq轴中

在本文中，同步参考系设定为由构网变流器1生成的旋转dq轴。进行构网变流器2 的建模时，需将式（1）中最后一个子式替换为式（6），其余保持不变。

式中：ω2为构网变流器2的旋转角频率。

式（1）—（6）建立了该微电网中构网型变流器的状态空间模型。通过在系统工作点附近对状态模型线性化，可以得到构网型变流器的小信号模型为

其中

式中：AI，BI，CI分别为该模型的状态矩阵、输入矩阵和输出矩阵；vbDQ为DQ轴中各节点电压所构成的向量；ΔioDQ为DQ轴中各构网型变流器输出电流值构成的向量。

1.3 基于跟网型变流器的子系统小信号模型

基于跟网型变流器的子系统包含1 个CPL、1 个跟网型变流器和1 个LCL 滤波器。CPL 可由DC/DC变流器接入直流母线并由DC/DC 变流器控制其功率的输入、输出。CPL具有负阻抗特性，当功率较大或在负荷中占比中较大时会对系统稳定性造成影响，其输出电流可由一个可控电流源表示，表达式为

式中：Pcpl为CPL的功率；vdc为直流母线电压。

如图3 所示，跟网型变流器的控制系统包括锁相环、abc三项坐标系与dq轴的转换模块、级联的电压电流环以及PWM信号发生器。

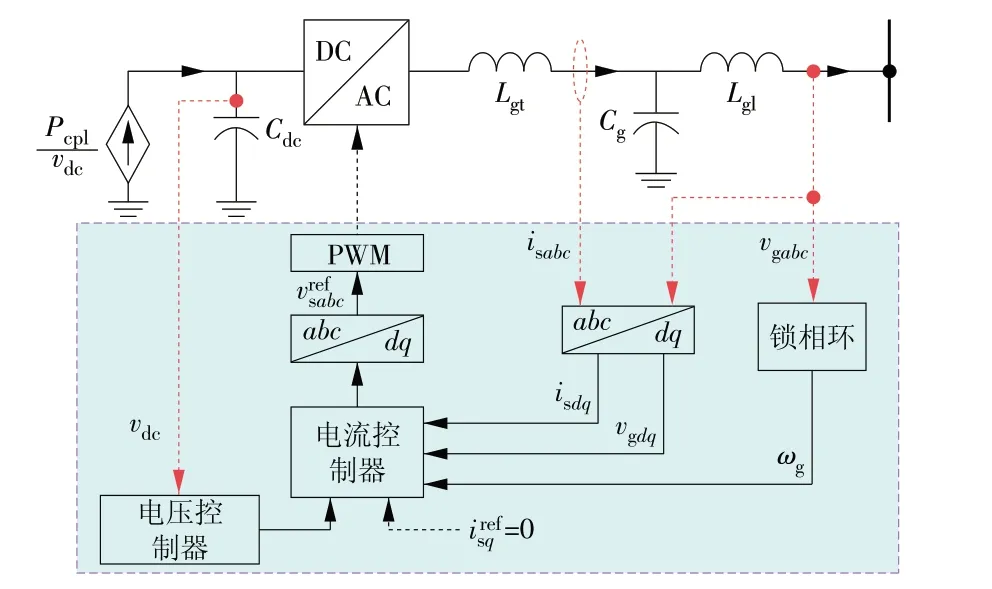
图3 跟网型变流器及控制系统Fig.3 Grid-following converter and its control system

通过锁相环可以跟踪节点电压频率，实现abc三项坐标系到dq坐标系的转换。锁相环的数学表达式为

式中：ρ为连接点的实际相角；ρ͂为锁相环估计的相角；xρ为锁相环PI 控制器积分环节的输出；ωg为锁相环跟踪得到的PCC处电压角频率；klp，kli分别为控制器的比例和积分参数。

控制系统中的外环电压控制器控制直流侧的电压并产生d轴的电流参考值，而q轴电流参考值一般情况下可设为0。将dq轴的电流参考值输入内环电流控制器，并产生变流器的控制信号。该控制系统的数学表达式为

式中：ξ1，ξ2，ξ3分别为外环电压控制器和内环电流控制器中PI 补偿器在dq轴中的积分；vsd，vsq分别为跟网变流器侧在dq轴的输出电压；isd，isq分别为跟网变流器侧在dq轴的电流；vcd，vcq分别为滤波器电容电压在dq轴中的值；vrefdc为DC 侧电压参考值；vdc为DC侧电压；irefsq为q轴电流参考值，一般可设为0。

跟网型变流器交流和直流侧的动态模型为

式中：igd，igq分别为电网侧在dq轴中的电流；Pcpl为CPL的功率；Cdc为直流侧电容。

基于跟网型变流器的子系统在dq轴的输出也需要通过式（4）转换到同步DQ轴中，并且式（4）中的δi需替换为ρ͂-θ。此外，式（15）中的vgd，vgq是DQ轴中得到的PCC 电压通过式（6）转换到dq轴得到的。根据式（12）—（15），在平衡点附近对该状态空间模型线性化后，可得到基于跟网型变流器子系统的小信号模型为

式中：AF，BF，CF分别为该模型的状态矩阵、输入矩阵和输出矩阵；ΔigDQ为电网侧电流在DQ轴中的值。

1.4 系统线路小信号模型

图1中线路i（i=1，2）的状态空间模型可表示为

可得到线路i的小信号模型为

其中

式中：ΔilineDi，ΔilineQi分别为线路i的电流在DQ轴中的值；vbDl，vbQl，vbDr，vbQr分别为线路i左节点和右节点的电压在DQ轴中的值。

1.5 孤岛微电网完整小信号模型

通过假设对地虚拟电阻［20］，节点j（j=1，2，3）的电压可定义为

式中：RN为假设的对地虚拟电阻值。

综合前文推导得到的基于构网型变流器和基于跟网型的子系统模型以及系统网络模型、节点电压定义，可以得到整个孤岛微电网的小信号模型为

式中：AW为该孤岛微电网模型的状态矩阵。

2 孤岛微电网小信号稳定性分析

2.1 全阶小信号模型分析

通过判断小信号模型特征值的符号可以直观得到系统的小信号稳定性。若小信号模型的特征值实数符号均为负，则系统为小信号稳定；否则，系统为小信号不稳定。系统参数见表1，参数的计算和取值可参考文献［21］。根据式（24）的小信号模型及系统参数可以得到特征值分布，如图4 所示。由图4 可以看出，系统的特征值均位于复平面左半平面。因此，在给出的参数及工作点下，该孤岛微电网为小信号稳定。

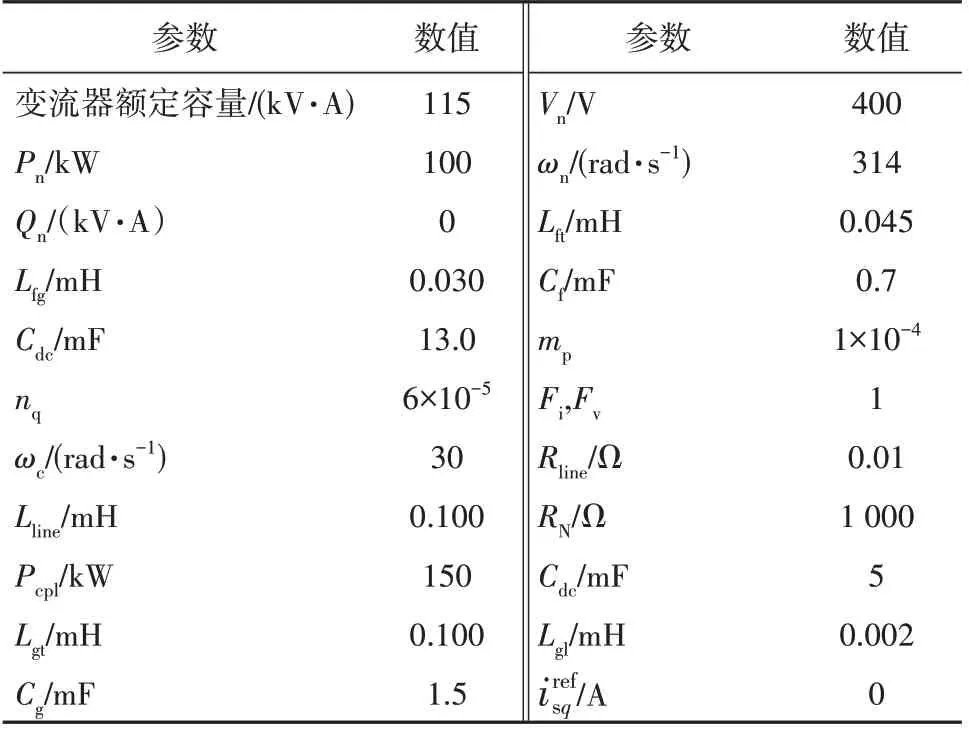
表1 系统参数Table 1 System parameters

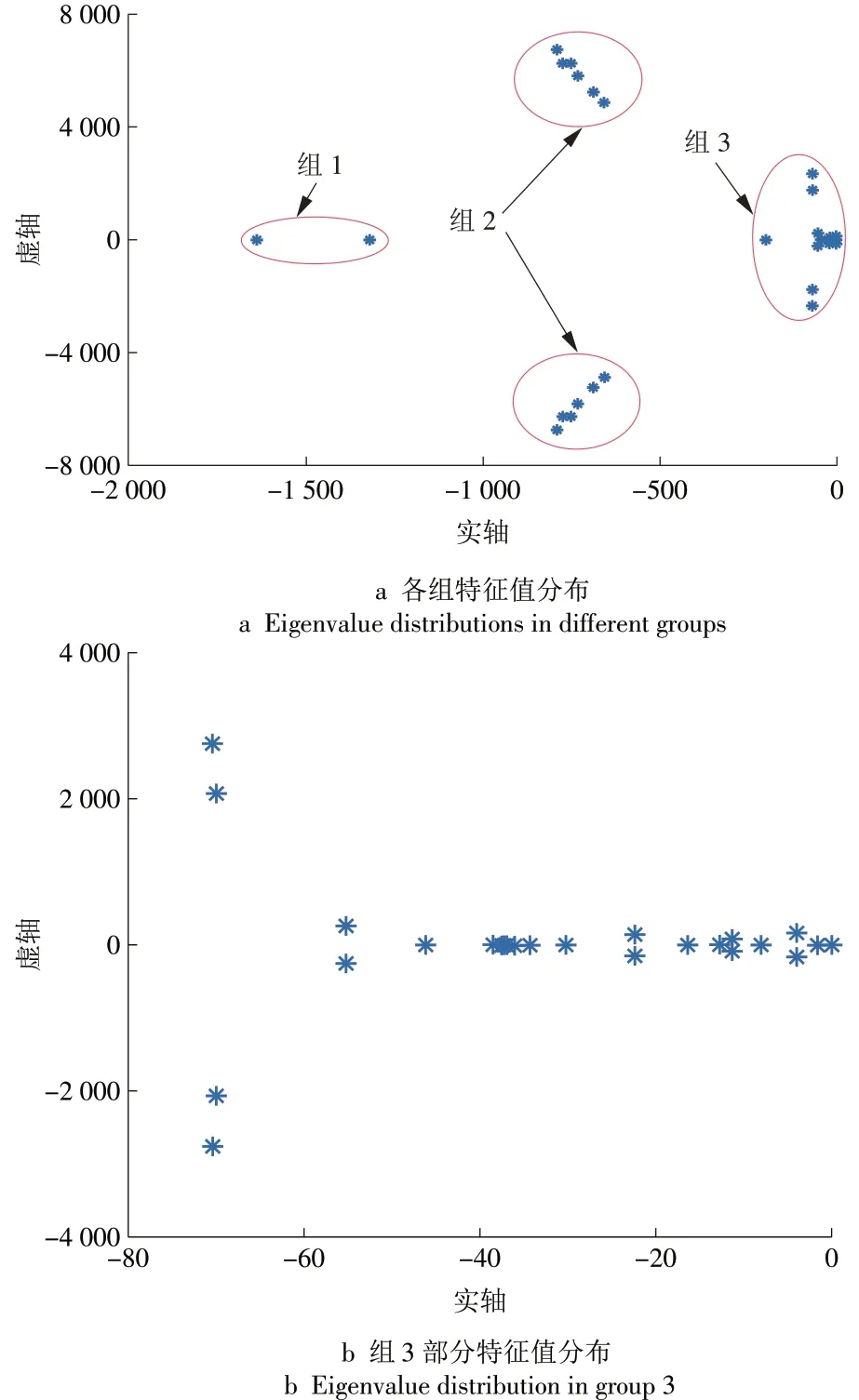
图4 系统特征值分布Fig.4 Eigenvalue distributions of the system

此外，本文引入了参与因子法分析系统状态变量与特征值之间的关系。参与因子的定义为

式中：λi为模型第i个特征值；akk为AW矩阵的对角元素；pki为第k个状态变量对第i个特征值的参与因子。

根据式（25）计算可知，图4 中组1 的特征值与构网型和跟网型变流器的内环电流控制器有关，组2 的特征值与各变流器外环电压控制器以及LCL 滤波器有关，而组3的特征值与CPL 的功率、构网型变流器中下垂控制系数以及线路阻抗有关。由于组1和组2 的特征值距离复平面中虚轴较远，其动态过程衰减较快，因此对系统的稳定性影响较小。而组3 的特征值距虚轴较近，说明恒下垂系数、线路阻抗及负荷功率对系统稳定性影响较大，在其设计不合理的情况下，组3特征值可能到达复平面右半平面，系统会出现小信号不稳定的情况。

由于下垂系数的绝对数值较小，对系统稳定性影响较大且调值裕度小，因此，本文将着重分析下垂系数的选取对系统小信号稳定性的影响。其余状态变量或参数对系统稳定性的影响可利用相同的方法进行分析。

2.2 下垂系数的影响分析

图5 显示了组3 中一对共轭复数特征值λ1，λ2在mp变化下的变化轨迹。可以看出，在mp从1.0 ×10-4变化到5.0 × 10-4的过程中，λ1，λ2逐渐向虚轴靠近，并在mp= 4.6 × 10-4时，系统处于稳定边界。mp＞4.6 × 10-4时，将大概率使λ1，λ2越过虚轴到达右半平面，造成系统的小信号不稳定。

图6 显示了nq逐渐从6.0 × 10-5变化到2.0 ×10-4的过程中，组3 中一对共轭复数特征值λ3，λ4的变化轨迹。从图6 可以看出，nq＞1.5 × 10-4时，λ3，λ4将到达复平面右半平面，导致系统失稳。

图6 nq变化对特征值的影响Fig.6 Impact of nq on the eigenvalue

通过以上分析可知，构网型变流器中较大的mp和nq可能导致系统小信号不稳定。为保障该孤岛微电网小信号稳定，mp的上界取值为4.6 × 10-4，nq的上界取值为1.5 × 10-4。值得注意的是，本文通过递增下垂系数的方法得到的数值上界非解析值，可通过调整递增精度得到更精准的上界值，但本文得到的结果已满足实际应用需求。

3 仿真验证

在Matlab/Simulink 中搭建该孤岛微电网的开关模型，并通过时域仿真结果验证分析的准确性。

本文设计了2个操作情景来分别验证上节中得到的mp和nq取值上界。情景1 中，mp在0 — 0.1 s的值为4.4 × 10-4，0.1 s 后增加到4.7 × 10-4。从图7 的仿真结果可以看出：0 —0.1 s 系统处于稳态，0.1 s后，基于跟网型系统直流母线的电压和系统频率均振荡增大，说明系统失稳；0.1 s 时系统频率出现阶跃变化，这是由于mp的改变同时改变了构网型变流器的输出频率。该仿真结果证明了上节分析得到的mp上界值的准确性。

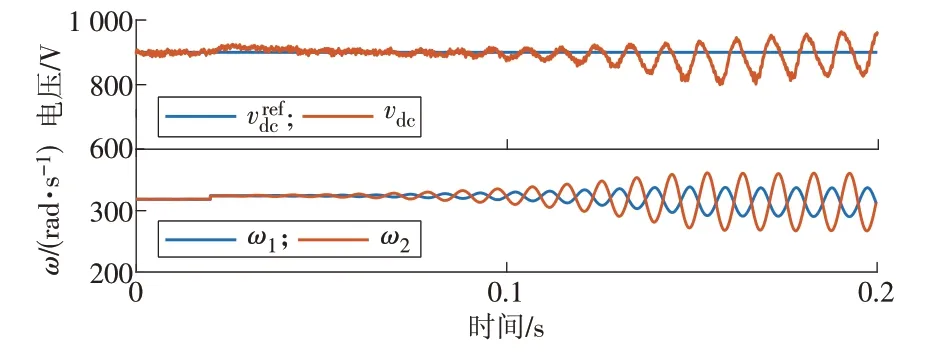
图7 情景1仿真结果Fig.7 Simulation results of scenario 1

情景2 的仿真目的是验证nq取值上界的准确性。0— 0.1 s，nq为1.3 × 10-4，0.1 s 后变为1.7 ×10-4。从图8 可以看出，系统在nq= 1.7 × 10-4时失稳，验证了上文分析得到的nq取值上界的有效性。

图8 情景2仿真结果Fig.8 Simulation results of scenario 2

4 结论

本文研究了基于构网型变流器和跟网型变流器并考虑CPL 的孤岛微电网小信号稳定性。通过特征值分析法和参与因子法，研究了构网型变流器中下垂系数对系统稳定性的影响，并得到其取值上界。本文主要结论如下。

（1）建立了包括构网型和跟网型变流器及CPL的孤岛微电网全阶小信号模型，该模型充分考虑了变流器与系统网络及负荷间的交互；本文建模基于一个特定的微电网，但建模方法适用于其他包含构网型和跟网型变流器的微电网。

（2）通过特征值分析法和参与因子法揭示了系统的稳定性以及主要的状态变量对稳定性的影响，可为调节其他系统参数或控制参数提供参考。

（3）本文以下垂系数的设计为例，通过特征值轨迹分析，得出较大的下垂系数会导致系统小信号不稳定的结论，并得到了下垂系数的数值上界。

限于篇幅，本文仅分析了下垂系数对系统稳定性的影响。根据小信号分析的结果，CPL 及线路阻抗也对系统的稳定性有较大影响，需要通过小信号分析给出合理取值范围。此外，当系统受到大扰动时，小信号分析不能预测系统稳定性，在这种情况下，应该采用大信号稳定性分析系统的稳定性。