考虑长期负荷概率预测的储能多阶段优化配置

李益民，董海鹰*，丁坤，王金岩

（1.兰州交通大学 新能源与动力工程学院，兰州 730070； 2.国网甘肃省电力公司电力科学研究院，兰州 730070）

0 引言

随着大规模高占比的新能源建成并网，对电力系统的安全稳定运行提出严峻挑战。风电、光伏的间歇性和波动性给电力系统带来巨大的不稳定因素，大规模储能系统对于风光的波动平抑，电力系统的削峰填谷起着重要作用［1］。其中，在电网侧的储能系统往往功率和容量较大，其初始配置的投资成本和后期运行的收益决定着储能投资运营商的意愿［2］。

针对储能的容量配置，国内外已有相关研究且方法多样。文献［3］以储能经济性为目标，建立了混合储能系统模型，通过与单一储能对比证实了混合储能系统在稳定性和经济性方面具有明显优势。文献［4］以总净现值成本最小为前提，对能源利用率和负荷损失率进行评价，建立含氢储能和蓄电池的混合储能模型，以降低微电网的运行成本。文献［5］以混合储能系统电能交互成本和储能投资运行成本最低为目标，应用离散傅里叶变换将原功率分解，对储能系统的充放电功率进行优化。文献［6］通过最小化储能初始投资和联络线波动，建立了储能容量配置模型。文献［7］提出了基于多代理系统的微电网竞价优化策略，从微电网的系统层次对发电成本进行讨论。文献［8］设计了一种储能电池参与一次调频的充放电策略，从电网频率信号波动特性出发，在确定的电网调频及储能电池运行要求约束下，得出调频效果最优、经济性最优目标下的储能电池容量配置方案。文献［9］从电力市场化的角度出发，提出了一种具有协调规划和运行的电网侧电池储能系统的双层优化选址和规模模型。文献［10-11］提出了一种考虑一次调频速率特性的电池储能系统容量优化配置方法，以提高电力系统的调频能力和性能。文献［12-13］分别对电网侧和微电网进行电价相关的储能优化配置。文献［14］分析了独立储能现货套利和辅助调频的市场机制。文献［15-16］从微电网变流器的结构和控制入手进行储能优化配置。

以上方法大多从改进混合储能和调度策略着手，均在稳定性和经济性的优化上取得了良好的效果。但是对于电网侧的储能配置，忽略了负荷增长带来的影响。在上述研究的基础上，本文提出了一种考虑长期负荷概率预测的储能多阶段优化配置方法，用于电网侧独立储能系统的容量配置。以独立大规模储能的成本和效益之和最低为目标，采用非参数组合回归的长期负荷概率预测模型，将“十四五”期间分为3个阶段，在此基础上对甘肃省酒泉地区进行多阶段储能优化配置，用改进的粒子群算法（PSO）求解，最后用酒泉地区的电力节点系统进行算例分析，验证方法和模型的可行性和优越性，并分别从峰谷电价差和新能源利用率两个方面对储能投资回本周期进行了灵敏度分析，为酒泉地区的储能规划提供一定的参考。

1 独立大规模储能成本效益分析

电网侧独立储能功率和容量一般较大，其初始配置成本和运行收益大［17-18］，本文从独立储能电站的视角出发，将规划周期T分为n个阶段对其进行多阶段成本效益分析。

1.1 储能全寿命周期成本

储能的成本模型主要由储能的能量成本和功率成本两部分组成［19-20］，当计及储能折旧后的剩余价值时，在第i阶段的投资成本可用式（1）表示。式（3）对式（2）中的成本部分进行了说明：

（1）容量成本仅与一次性投资成本相关；

（2）功率成本由建设成本和运行维护成本两部分组成。当采用多阶段规划，部分设备在规划周期外依然具有使用价值，因此计及设备的使用情况。

式中：，ψ为设备的折旧系数，1-ψ为未利用价值系数［21-22］；分别为储能的功率成本与容量成本；分别为在i阶段储能装置的功率与容量；cP，cS分别为初期储能的单位功率成本和单位容量成本；βj为第j年运行维护费用相对于初期功率成本的折算系数；k为通货膨胀率；d为贴现率；ti为规划期内设备的使用时间；τbat为说明书上的使用年限。

1.2 储能运行经济效益

独立储能在电网侧的收益主要有3 个方面：现货市场峰谷电价套利收益、调频辅助服务收益和延缓电网投资建设收益［23-24］。

1.2.1 电力市场峰谷电价套利

在峰谷电价下，储能系统的“填谷”和“削峰”获得的套利收益为

式中：Bdis，i为第i阶段放电的售电收益；Ccha，i为第i阶段充电时的购电成本。

在负荷峰值期间，通过释放储能中电能缓解电网压力，在电力市场环境下，售电收益为

式中：Pdis(t)为时刻t储能装置提供给电网的功率；Cpeak，t为峰值时t储能装置的售电电价；ηdis为储能装置的放电效率；Ti为第i阶段的总小时数。

利用储能装置的负荷特性，提高在电源出力高峰时期的电网消纳能力，在负荷非高峰时，储能系统吸纳上级电网的电量，在电力市场环境下的购电成本为

式中：Pcha(t)为t时刻储能装置吸纳的功率；Coff，t为低谷t时刻的电价；ηcha为储能充电效率。

1.2.2 调频辅助服务收益

电池储能比传统火电机组和水电机组具有更快的响应和爬坡能力，可以辅助电力系统进行调频。目前中国的电池储能调频以一次调频为主，各省份政策对储能参与一次调频的主体地位尚未明晰，全国统一电力大市场尚在完善，大多省份要求在一天内储能只能参与现货电能市场或者调频辅助市场，二者不可同时参与，且日前的调频能量投标涉及调度，本文在此不予考虑。

1.2.3 延缓电网投资建设收益

电力系统升级是为了满足不断增长的负荷需求［14］，但利用储能装置在提高风光渗透率的同时实现了削峰填谷，从而延缓了电网建设。虽然各个阶段均由延缓电网升级的作用，但随着时间的推移，多阶段的累加，将导致该收益的重复计算，因此仅在最后阶段进行计算。因此，延缓电网建设的收益模型可写为

2 长期负荷概率预测模型

本文基于多维变量筛选-非参数组合回归组合的长期负荷概率预测模型，结合多阶段规划方法，对甘肃酒泉地区的长期负荷进行概率预测，得到不同分位点值的负荷。

2.1 非参数组合回归模型

长期负荷发展受多个因素共同影响，若采用单个因素映射得到的一维非参数回归模型对长期负荷进行预测，其精度不能满足要求。文献［23］对经济因素、人口因素、技术因素、市场因素和气候因素中包括的14 个具体因素进行Granger 因果分析，发现国内生产总值（GDP）、三产占比、人均消费支出、常住人口、城镇化率和消费者价格指数（CPI）这6个变量与电量序列同阶平稳，再初步增大滞后期，发现这6个变量对电量具有拉动关系或者电量对其有拉动关系，认为这6 个变量为电量的Granger 因，表明其对长期负荷具有显著驱动作用。然后对这6个一维非参数模型根据预测精度进行优先级排序。在此基础上，采用逐步平均组合法对这些一维非参数回归模型进行不同的组合，得到的非参数组合回归模型为

式中：mj(·)为第j个影响变量映射下的一维非参数回归函数；J为影响变量总数；k为进行平均组合的模型数目，取1，2，…，J；其中第k个非参数组合回归模型中的k个进行组合的一维非参数回归模型，对组合后的J个非参数组合回归模型的预测精度进行评价，选择其中精度最高的组合模型作为最优非参数组合回归模型。在6个影响因素中选取最优组合回归模型的变量为GDP、人均消费支出、CPI 和城镇化率［23］。

2.2 基于随机变化率的不确定性建模

影响因素的不确定性等价于其变化率的不确定性，本文基于随机变化率对影响因素进行不确定性建模［20］。

考虑到影响变量的随机变化率受多个独立的且不能产生支配性的因素共同作用，因此可认为随机变化率近似服从正态分布。文献［23］用历史变化率的标准差代替未来变化率的波动，未来变化率的均值则按照影响变量是否有规划值来确定。

（1）若有未来规划值，结合当前年的时值，求算未来年平均增长率，以此作为未来随机变化率的均值。

（2）若没有未来规划值，按历史变化率的均值作为未来变化率均值。此外，为了模拟未来影响因素的不确定性，对影响因素的随机变化率进行不确定性建模，将等概率抽样得到随机变化率还原为影响变量逐年的等概率值。还原过程如下。

假设对未来T年进行N次模拟，得到随机变化率模拟矩阵R，再通过式（10）逐年累乘方法得到随机变化率的乘子矩阵

式中：E为元素全为1 的矩阵；prod为对前t行（1≤t≤T）逐列进行累乘。将当前年影响变量的时值乘上乘子矩阵M，则可得到影响变量逐年的等概率值。

2.3 长期负荷概率预测综合实现流程

本文采用的长期负荷概率预测实现流程如下。

（1）利用Granger因果分析进行影响因素的多维变量初步筛选，确定变量维数J。

（2）对J个变量组成的一维非参数模型根据预测精度进行优先级排序，然后采用逐步平均组合法对不同的非参数模型进行精度校验，确定最优的非参数组合回归模型和对应的影响变量。

（3）利用图1的不确定建模流程，对影响变量进行N次等概率模拟，获取未来影响因素等概率序列，将其代入非参数组合回归模型实现长期负荷不同分位点值的概率预测。

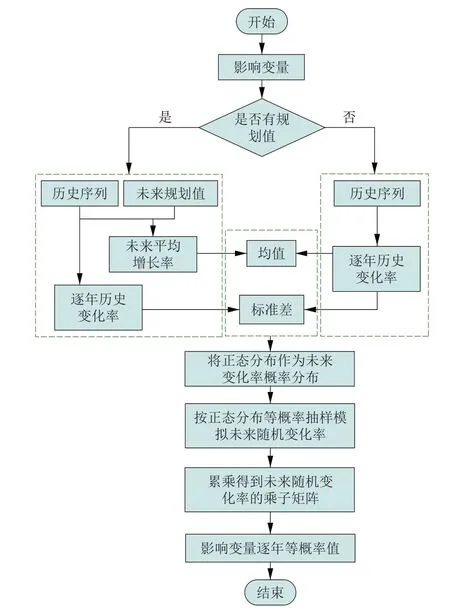
图1 基于随机变化率的不确定建模流程Fig.1 Uncertain modeling based on random change rate

3 考虑长期负荷概率预测的储能多阶段模型

3.1 多阶段规划目标函数

本文提出的计及负荷预测的储能容量配置流程如图2 所示，Count为设置的迭代次数，此处Count=100。在模型的初期，需要对多阶段进行划分，以“十四五”为规划周期，分成3个阶段。

图2 多阶段储能优化配置流程Fig.2 Multi-stage energy storage optimal configuration

各阶段包括规划层和运行层，用运行指导规划。阶段内，以成本效益函数最低为目标，以系统电力电量平衡，风光火储的运行等条件为约束，优化求解总规划周期内的储能容量配置。下一阶段的预测负荷更新上一阶段的负荷，对储能的规划和运行产生影响。在多阶段规划的目标函数中，各阶段的规划层成本减去运行层收益的数值再求和最小，表明在规划周期内储能配置经济性最佳。以储能经济性最优为目标函数

3.2 约束条件

3.2.1 系统功率平衡约束

3.2.2 储能运行约束

式（14）和（15）约束了储能荷电状态的上下限，对储能的功率进行约束，式（16）表明储能在1 d 的开始时段和结束时段的荷电状态保持相同。

3.2.3 系统电压约束

式中：Ui(t)为系统各节点电压；Uimin(t)和Uimax(t)为节点电压的最小值和最大值。

3.3 求解算法

本文采用改进的PSO算法求解。采用PSO求解不同的问题时，对局部最优能力和全局最优能力的权衡也不一样，针对这个问题，在速度更新公式中添加了一个惯性权重

式中：x，v分别为位置和速度，均为向量；w为惯性权重；L1，L2为学习因子；r1，r2为［0，1］区间均匀分布的随机数；vi，t为上一轮迭代结束时的速度；()为社会学习向量；()为自我学习向量。

4 算例分析

为了验证长期负荷概率预测模型和储能的多阶段优化配置，本文搭建了甘肃省酒泉地区的电力节点系统进行仿真验证。具体的电力拓扑如图3所示，包括15 个火电厂、8 个风力发电厂和10 个光伏发电厂。

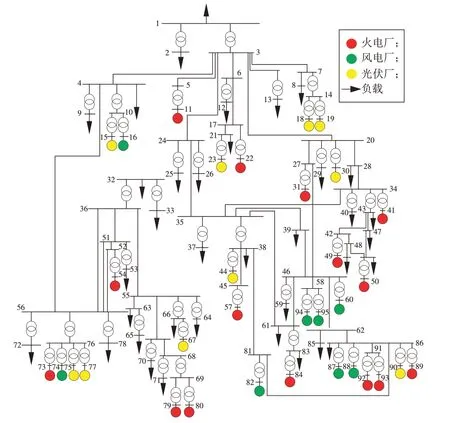
图3 电力系统拓扑Fig.3 Power system topology

本文的参数设置见表1，选取的2022 年甘肃省酒泉地区冬季某典型日的负荷和机组出力如图4所示，外送电量和净负荷如图5所示。

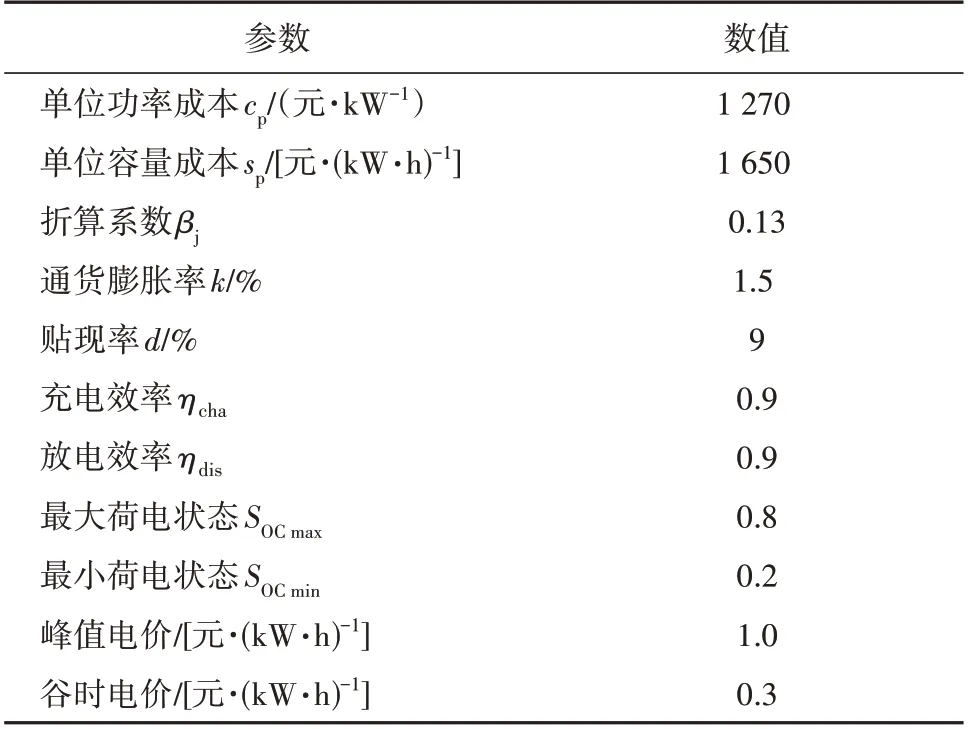
表1 参数设置Table 1 Parameter settings

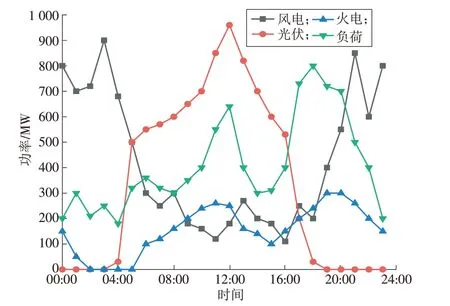
图4 冬季典型日的机组和负荷功率Fig.4 Typical daily load variation in winter

图5 冬季典型日的外送功率和净负荷Fig.5 Typical daily transmission power and net load in winter

图5 中，净负荷表示负荷和外送功率的和减去所有出力机组的差值，负数代表电源的出力大于负荷和外送功率的总需求。

4.1 长期电量概率预测分析

将本文的非参数组合回归模型与文献［24］的BP神经网络模型进行对比。2种模型对甘肃酒泉地区测试集的预测结果如图6所示。

图6 2种模型预测结果对比Fig.6 Model prediction results of two models

由图6 可知，对于酒泉地区2019—2022 年的实际用电量，非参数组合回归模型的预测精度为1.52%，小于BP 神经网络模型的，表明本文模型的预测精度较高。

通过随机变化率的不确定性建模，对酒泉地区2023—2025 年电量进行概率预测。根据本文提出的基于随机变化率的不确定建模方法，对上述4 个变量：GDP、人均消费支出、CPI 及城镇化率进行不确定性建模。结合酒泉地区统计年鉴及“十四五”规划报告，可得到“十四五”期间当地GDP、人均消费支出、CPI 及城镇化率。通过对各变量的变化率按正态分布进行200 次等概率抽样模拟，得到2023—2025 年共3 年的不同分位点值的预测电量，见表2。由表2 可知，50%分位点值与规划值最接近，代表平稳发展水平下的电量预测水平。

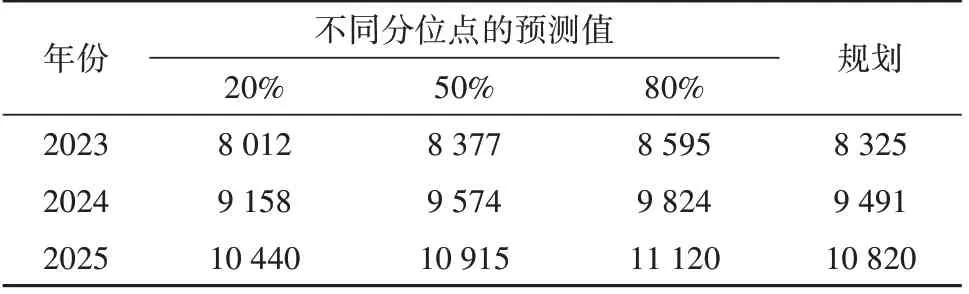
表2 不同分位点的预测电量Table 2 Power prediction results at different quantile levels GW·h

4.2 储能多阶段优化配置分析

本文设置粒子群算法总的迭代次数设为100，为了使得粒子群算法在初期具有较强的全局收敛能力，在后期具有较强的局部收敛能力，本文采用自适应调整惯性权重的策略，随着迭代次数增加，惯性权重线性减小，其最大、最小惯性系数分别为1.0，0.6，学习因子L1=L2=2，在配置的3 个阶段中每个阶段含有功率与容量变量，所以粒子的维度为6。以50%为负荷预测分位点值代入多阶段优化模型，各阶段的储能功率和容量见表3。

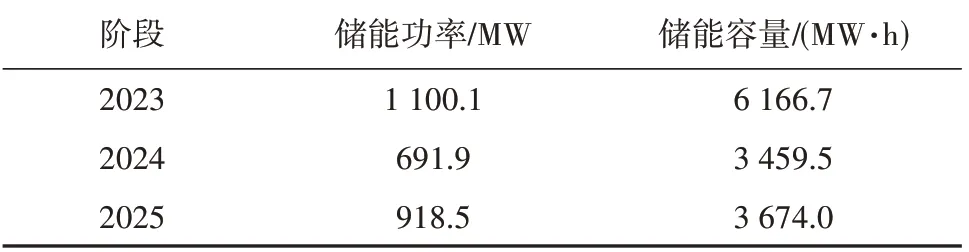
表3 各阶段储能配置功率和容量Table 3 Power and capacity configurations of energy storage at different stages

随着“十四五”期间的负荷增长，每年需要增加储能的配置以满足电力系统的供需平衡。根据表3，截至2025 年，甘肃省酒泉地区需要配置271.05 MW，13 300.2 MW·h 的储能。各阶段的典型日的储能荷电状态变化如图7所示。多阶段规划使得在各个阶段设备的利用率提高，可以通过调度过程中的SOC的变化来体现设备利用率。图7选取了3个阶段的冬季典型日的SOC变化情况来体现储能的利用情况。3 个阶段的最大SOC分别为0.749，0.782，0.800，与安全运行下的SOCmax=0.8差值逐渐缩小；相应的最小SOC为0.241，0.220，0.201，与安全运行下的SOCmax=0.2相差逐渐减小，说明考虑预测负荷的储能多阶段容量配置方法使得储能设备的利用率提高。多阶段容量配置在保证风电和光伏峰值时期的出力被充分利用的同时，实现了配套储能装置的充分利用，通过提高设备的利用率，实现了经济利益的优化。

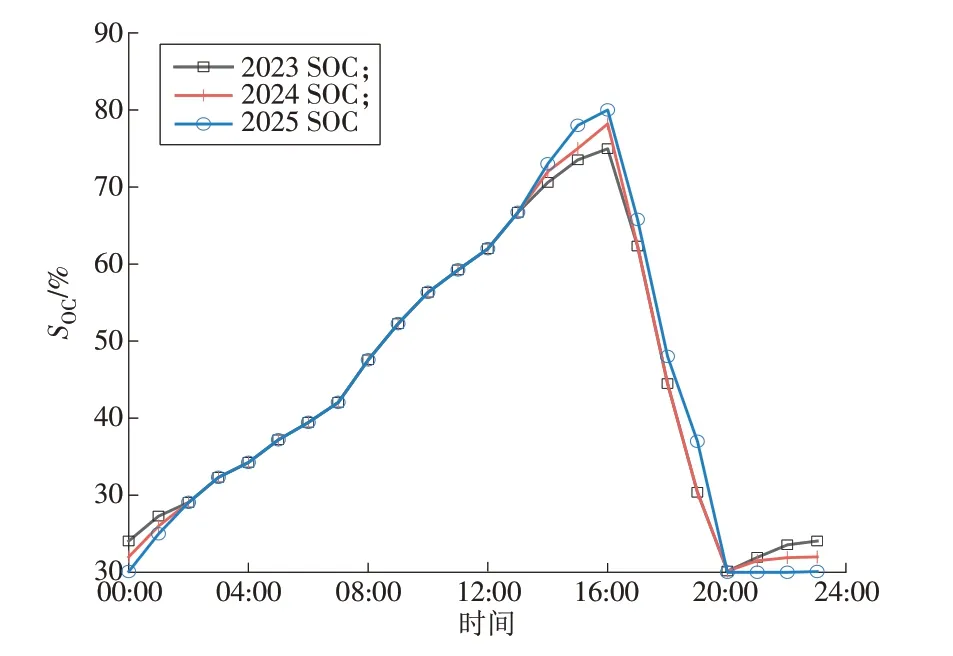
图7 各阶段储能SOC状态Fig.7 Multi-stage SOC

4.3 灵敏度分析

在储能的功率和容量优化配置中，不同的峰谷电价差会影响储能电站的盈利水平和回本周期，不同的新能源利用率也会对储能电站的初始投资规模和盈利水平产生较大影响。甘肃电网新能源的尖峰出力很大，但持续时间较短，如果追求过高的新能源利用率，会极大提高系统的备用率，带来过高的边际消纳成本，影响整个系统的经济性。下面从峰谷电价差和新能源利用率2个方面对储能规划的经济性进行灵敏度分析。

4.3.1 峰谷电价差

不同的峰谷电价差对储能电站的峰谷套利和回本周期影响较大，下面设置电价差从0.7 元/（kW·h）起始，以0.1 元/（kW·h）为步长，分析到1.5元/（kW·h）为止的储能电站回本周期，考虑建设成本和运维成本，以储能电站平均寿命20 年，年运行平均300 d为基准，结果如图8所示。

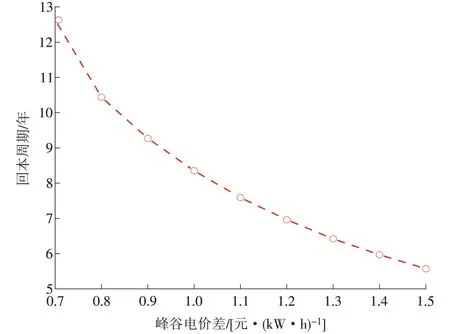
图8 峰谷电价差与储能回本周期的关系Fig.8 Sensitivity analysis on peak-valley electricity price difference

由图8 可以看出，参与现货电力市场的独立储能运营商，在峰谷电价差逐渐提高的过程中，其回本周期也大幅缩短。从0.7 元/（kW·h）逐步增大至1.5 元/（kW·h），可以发现储能的回本周期由接近12.63 年降低至5.57 年，这大幅缩短了投资商资金回流时间，提高了配置储能的经济效益。2023 年以来，山东省出现的负电价现象就是峰谷电价差提高的具体体现。在全国统一电力大市场机制逐步完善过程中，不同省份的现货电力市场政策差别较大，为了提升储能投资商的投资意愿，可以适当提高峰谷电价差。此外，在建设全国统一电力大市场的过程中，现货电力市场和辅助服务市场的联合出清优化体系也在逐步形成，可以更进一步地为储能投资商带来更好的市场环境。

4.3.2 新能源利用率

甘肃酒泉地区新能源渗透率高，本地负荷体量低，新能源小发期间电力供应不足和大发期间消纳困难的问题频繁出现，制定合理的新能源利用率，既可以提高系统经济性，也可以促进新能源的规模发展。下面从储能投资运营商角度考虑，以峰谷电价差为0.7元/（kW·h），分析新能源利用率与回本周期的关系，如图9所示。

图9 新能源利用率与储能回本周期的关系Fig.9 Sensitivity analysis on new energy utilization rate

由图9可以看出，适当降低新能源利用率，可以大幅减少储能的回本周期，在新能源利用率降低至98%时，由初始储能规模减小带来的投资降低与储能运行的收益降低达到平衡，回本周期开始上升［25-27］。

5 结论

本文针对甘肃省酒泉地区电网侧的储能配置提出了考虑长期负荷概率预测的多阶段规划方法，采用非参数组合回归的长期负荷概率预测模型，以“十四五”期间独立储能的经济性最优为目标函数，改进粒子群算法进行求解，分析了多阶段储能配置结果和峰谷电价差以及新能源利用率对储能经济性的灵敏度。得出以下结论。

（1）考虑负荷概率预测的储能多阶段优化配置方法可以更加真实地反映由电力电量平衡和调峰平衡带来的储能需求，对于储能的荷电状态利用更加充分。

（2）峰谷电价差和新能源利用率对于储能投资运营商的回本周期影响较大，适当合理地降低新能源利用率可以大幅提高储能优化配置的经济性。

（3）随着全国统一电力市场的完善健全，储能参与现货市场和辅助服务联合优化出清势必会进一步降低储能的回本周期，下一步将以此为突破点进行研究分析。