船舱隔壁螺旋槽旋转密封装置密封性能优化

曲佳辉，武兴伟，高珍，侯天柱，陈武超，李松山

(1.中国船舶集团有限公司第七一一研究所，上海 201108；2.中国船舶及海洋工程设计研究院，上海 200010)

船舱隔壁密封装置一般用于阻止海水进入隔壁舱室，旋转密封环作为隔壁舱室轴密封装置的关键部件，起着防止流体介质泄漏和降低能耗的关键作用。机械密封具有泄漏量少、可靠性高、寿命长等优点，其作为最主要的轴密封方式之一，被广泛应用于船舶、汽车、石油化工、航空航天等领域[1-5]。

螺旋槽密封作为一种常见的机械密封型式，具有优良的流体动压效应和液体泄漏控制效能[6-9]。WANG等[10]通过采用一种针对冲突目标的多目标优化方法来优化特定样本的螺旋槽，解决了因提高气膜升程或膜刚度引起泄漏增加的问题。赵一民等[11]基于Elrod空化算法研究了螺旋槽结构参数对旋转密封性能的影响规律，获得了旋转密封螺旋槽的结构优化取值范围。李振涛等[12]基于质量守恒的JFO边界条件建立考虑表面粗糙度的螺旋槽液膜密封物理模型，分析了螺旋槽开槽位置及空化压力对液膜中空化发生的影响，结果表明，螺旋槽位置对空化的影响与螺旋槽功用密切相关。陈源等人[13]通过小扰动法建立螺旋槽干气密封微扰膜压控制方程，在高速高压条件下，分析了螺旋槽结构参数对气膜动态特性系数的影响规律，并以端面膜厚最大扰动量峰值和扰动稳定时间作为目标函数对螺旋槽结构参数进行了优化。孟祥铠等[14]研究了螺旋槽机械密封液膜动力学特性，建立了考虑液膜空化的密封微扰膜压控制方程，采用有限单元法对端面液膜三自由度微扰下的液膜刚度和阻尼系数进行了数值求解，分析了不同参数对液膜密封动力系数的影响。徐奇超等[15]基于遗传算法建立了双向旋转槽干气密封的几何模型和数学模型，采用有限差分法求解端面膜压控制方程，获得了开启力和气膜刚度等稳态性能参数。许晓东等[16]研究了螺旋槽旋转密封装置槽型结构参数对液膜机械密封汽化特性的影响规律，基于均匀试验设计方法和响应面法探究了槽型结构参数之间交互作用，并以平均汽相体积分数为优化目标，采用遗传算法获得了结构参数最优解范围。

Box-Behnken设计作为一种实验寻优方法，根据一定的试验数据通过多元二次回归方程拟合因素与响应值间函数关系，在因素和响应值之间存在多元非线性关系时可快速准确寻找最佳试验条件，预测多变量下最优响应值。Box-Behnken响应面优化方法[17-19]通过合理的试验安排大幅提高试验效率和产品性能，在生物、化学和能源等行业以及新产品、新工艺、新材料等专业领域的研究中得到了广泛应用。但目前鲜有将该方法用于机械密封装置密封性能试验设计研究，也未见到将该方法用于旋转槽密封装置密封性能试验研究。

鉴于目前尚未见到螺旋槽密封装置应用于船舱隔壁密封的研究，为探究适用于船舱隔壁密封安装型式和旋转轴大直径特点的实际密封性能，本文作者设计了一种螺旋槽式旋转隔壁密封装置，通过对螺旋槽旋转密封性能理论模型的数值求解，初步分析了旋转槽单一结构参数对样机泄漏量、液膜承载力和液膜摩擦转矩的影响规律；采用Box-Behnken响应面优化方法对其密封性能进行试验设计，通过试验数据统计分析，建立螺旋槽式旋转隔壁密封装置密封性能数学模型，深入分析了槽数、槽台比、槽坝比、槽深比和螺旋角及其交互作用对装置密封性能的影响程度大小和影响规律，获得旋转槽结构参数最优组合方案和密封装置最低泄漏量；考虑工程实际中允许在最低泄漏量基础上增加一定幅度，将其作为优化限制条件，采用遗传算法获得了螺旋槽最优取值范围，以期为该类密封装置在船舶领域的设计和工程使用提供参考。

1 螺旋槽密封装置设计及理论分析

图1所示为旋转机械密封原理，图2所示为设计的螺旋槽旋转密封结构。旋转密封环安装于进油衬套与旋转轴间的凹槽中，通过润滑油挤压推动，凹槽内壁与密封环端面相互贴合形成密封面，阻碍流体泄漏，起到密封旋转轴与固定件的作用。图中，rg、ri和ro分别为螺旋槽顶圆半径、密封环内径和密封环外径；h0和hg分别为最小液膜厚度和槽深；h为液膜厚度，槽区h=h0+hg，非槽区h=h0；θ1和θg分别为台区和槽区对应的旋转角度；β为螺旋角；Ng为槽数；ω为密封副角速度。定义，槽台比为δθ=θg/(θg+θ1)、 槽坝比为δr=(rg-ri)/(ro-ri)、 槽深比为槽深和最小液膜厚度之比，即Δ=hg/h0。

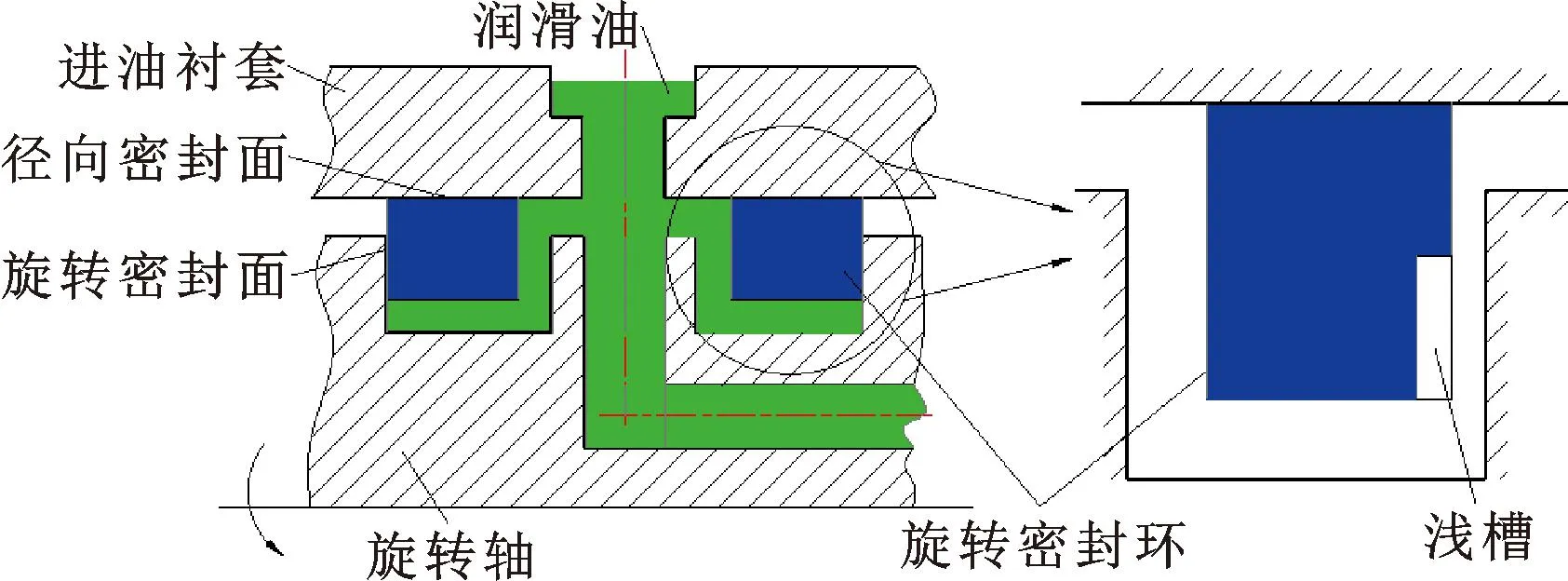
图1 旋转机械密封原理Fig.1 Principle of rotating mechanical seal

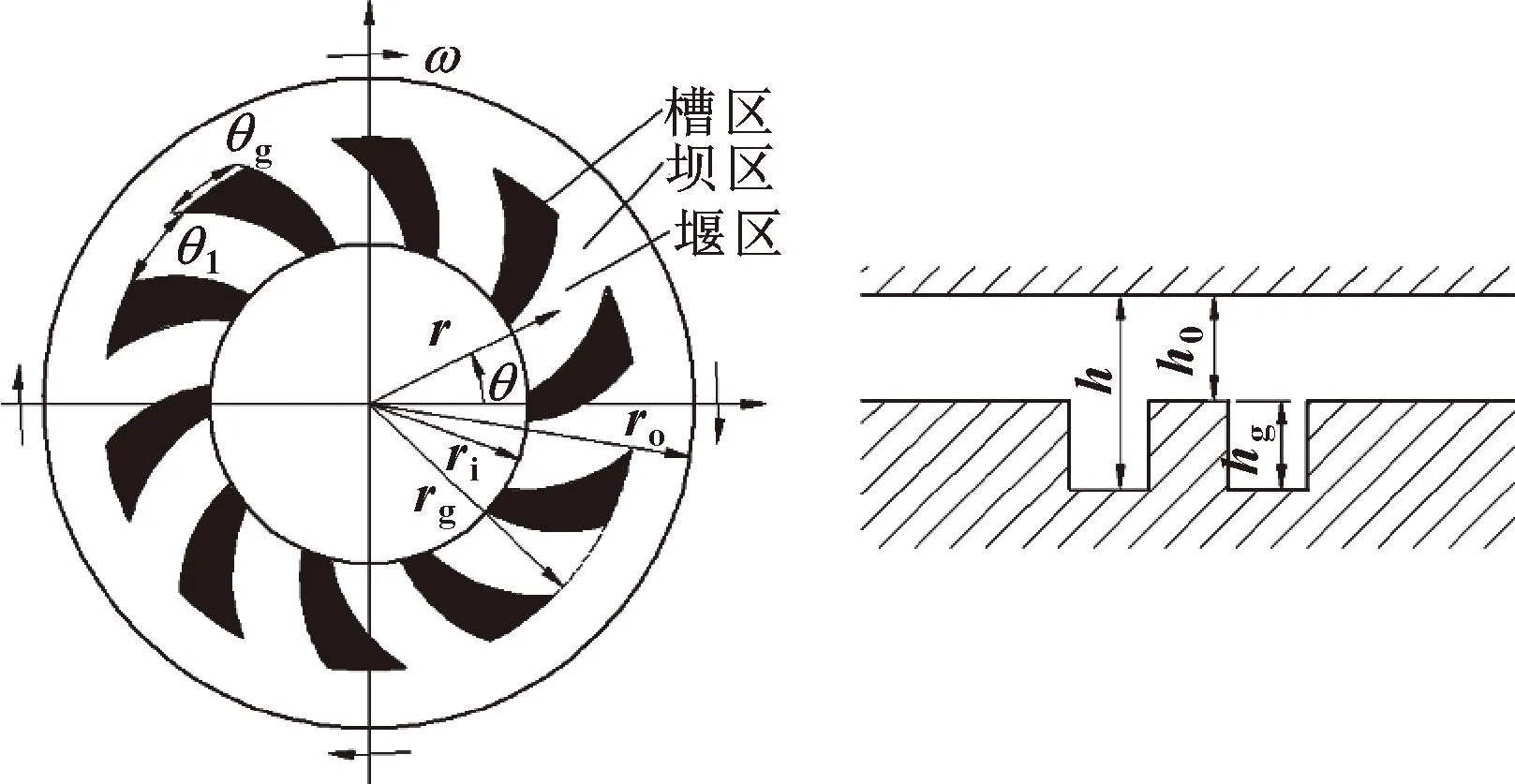
图2 螺旋槽旋转密封结构示意Fig.2 Schematic of spiral groove rotary sealing structure

常规使用情况下舱内无水，当旋转轴工作时，由空气和润滑油建立润滑密封面，当一侧舱室漏水时，已经建立的密封面起到密封作用，防止海水进入隔壁舱室。由于密封环槽台边界存在密封间隙的突变，发散间隙将导致液膜压力低于空化压力，此时将会出现空化区。实际空化区的存在一定程度上有利于降低泄漏量，整个流场则被分为完整液膜区和空化区，并通过引入通用变量φ和开关函数F来区分定义完整液膜区和空化区。

完整液膜区

(1)

空化区

(2)

式中：p′为液膜压力；p0为密封环外径压力；pc为空化压力；ρ为油液密度；ρc为润滑介质密度。

根据公式(1)(2)，当φ≥0⟹F=1，φ<0⟹F=0，在完整液膜区，F=1，φ为液膜压力分布；在空化区，F=0，1+φ表征了液气两相的混合比例。

由于螺旋槽的存在，物理计算区域是复杂的多边曲边梯形，需要通过贴体坐标变换方法，将其转化为规则区域，解决数值离散和迭代求解的困难。根据数值离散迭代方程可求出通用变量φ和开关函数F在计算域内的结果[11]。由此可以代入公式(3)—(7)求出船用螺旋槽式旋转隔壁密封装置密封性能参数，这些参数共同决定了该装置的密封、开启、稳定和经济等多种性能。

液膜承载力

(3)

液膜刚度

(4)

泄漏量

(5)

液膜摩擦转矩

(6)

公式(3)—(6)中量纲一化参数为

(7)

2 试验验证

2.1 样机试验系统和方法

设计的螺旋槽密封装置制作样机后在如图3所示的试验台架上进行试验。试验台架主要由驱动电机、齿轮箱、刚性安装支座、过渡法兰、转动轴、位移调整环、试验端盖、压力表、压力传感器、流量计、进水装置和密封工装等组成。齿轮箱用于控制旋转轴转速，流量计用于测量水的泄漏量，密封工装用于营造模拟舱内密封压力环境，压力表用于测试密封工装内的压力。

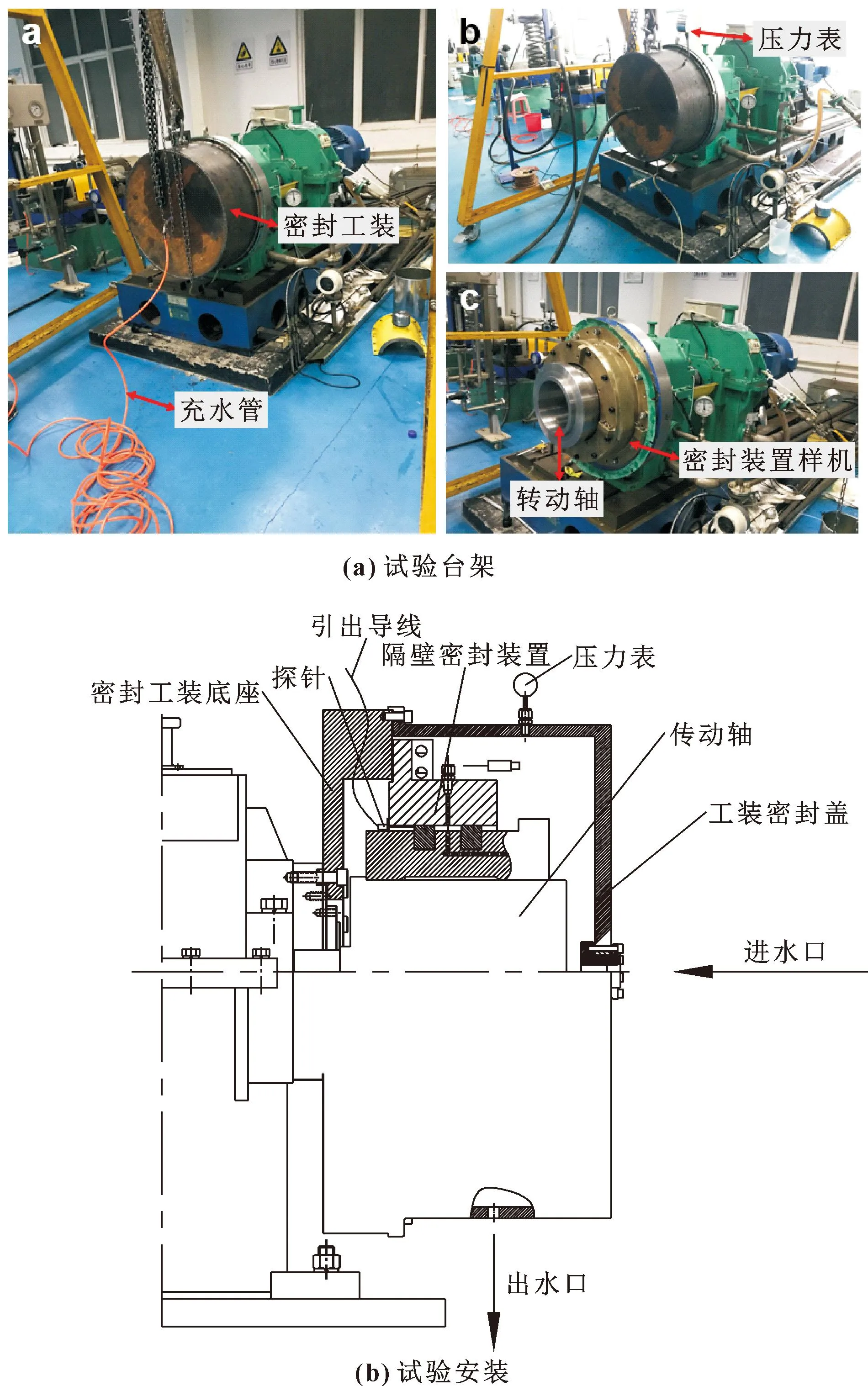
图3 密封性能试验布置示意Fig.3 Sealing performance test layout：(a)test bench； (b)test layout

将隔壁密封装置样机安装在试验台架上，一侧通入压力水，并设置收集通道用于收集经密封装置泄漏的水，测定水流量即为泄漏量。启动压力水泵，调节水压，使隔壁密封装置处水压为0.2 MPa；调节隔壁密封装置主轴转速为500 r/min；试验台保持连续运转，待工况稳定后，每2 min记录1次压力、泄漏量、环境温度、密封装置温度、水温及水泄漏量等。通过安装不同样机改变槽台比等试验因素；通过纳米位移传感器检测反馈改变油压逐步调整闭合力从而调节槽深比。不同工况下重复以上试验，获得试验样本数据。

2.2 泄漏量理论分析结果及验证

初始设计的螺旋槽式旋转隔壁密封装置结构参数为：槽数Ng=25，螺旋角β=35°，槽深比Δ=2，密封环内径ri=450 mm，密封环外径ro=485 mm，槽深hg=12 μm，槽台比δθ=0.35，槽坝比δr=0.45；物性参数和边界压力：润滑油黏度μ=0.02 Pa·s，润滑油密度ρ=884 kg/m3，密封环外径压力p0=0.1 MPa。以初步设计参数为基础数据，分别改变槽数、螺旋角、槽深比、槽台比和槽坝比，根据公式(3)—(7)可获得密封装置样机泄漏量、液膜承载力和液膜摩擦转矩随各参数变化的曲线，如图4—6所示。

从图4中可以看出，样机泄漏量随槽数、螺旋角和槽深比的增大均呈现出先增大后减小的规律，在极大值点两侧，泄漏量随各参数变化的快慢不同；泄漏量随槽台比和槽坝比的增大均呈现出增大的规律。样机泄漏量计算值与试验值基本一致，误差在5%以内，验证了理论分析的正确性。

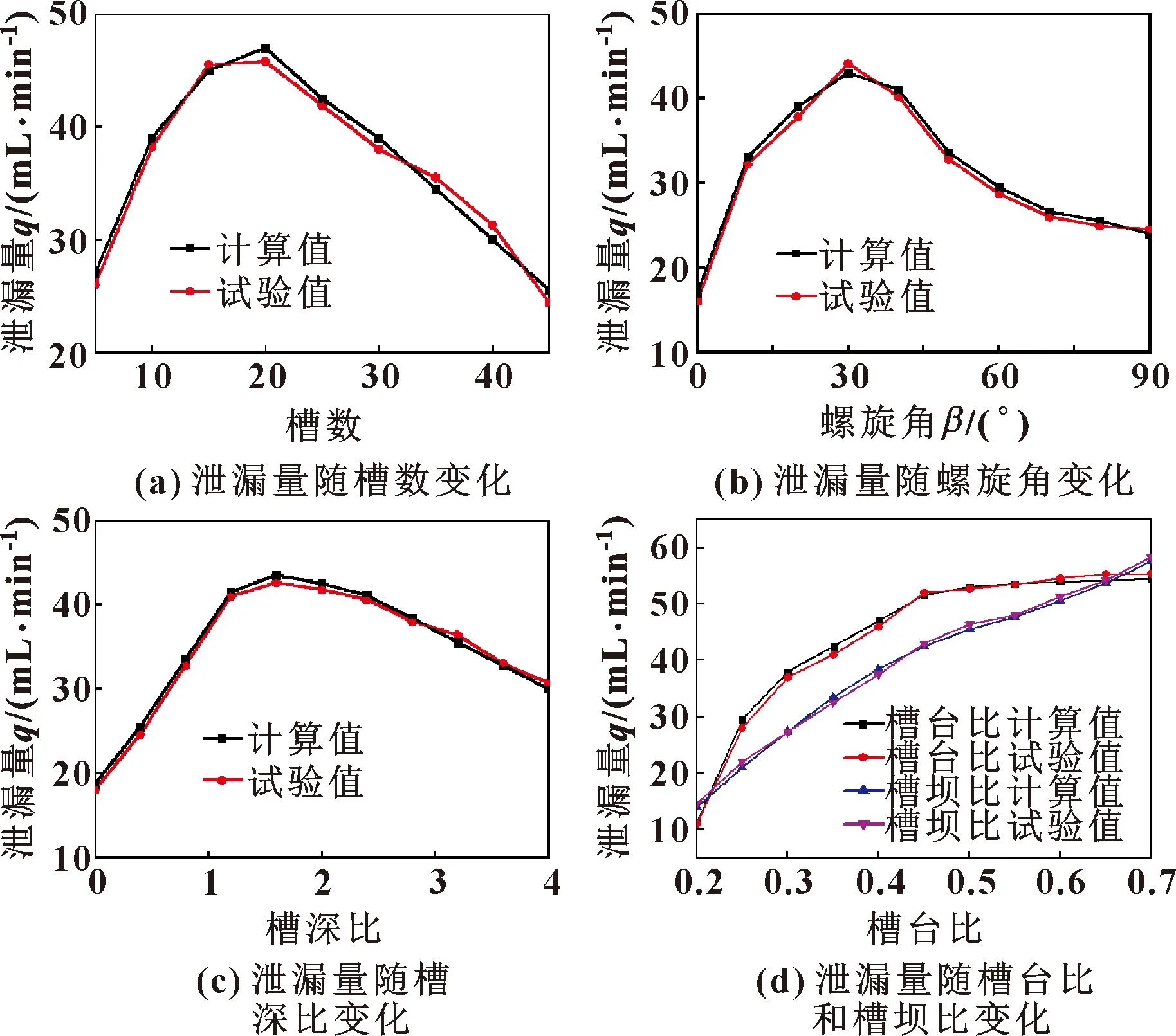
图4 泄漏量随槽数、螺旋角、槽深比、槽台比和槽坝比变化Fig.4 Variation of leakage with the number of grooves(a)，spiral angle (b)，the groove depth ratio(c)，the circumferential groove platform ratio and the radial groove platform ratio(d)

从图5中可以看出，样机液膜承载力随槽数、螺旋角和槽深比的增大均呈现出先增大后减小的规律，在极大值点两侧，液膜承载力同样随各参数变化的快慢不一；液膜承载力随周向槽台比的增大呈现出增大的规律，随槽坝比的增大呈现出先增大后减小的规律。

图5 液膜承载力随槽数、螺旋角、槽深比、槽台比 和槽坝比变化Fig.5 Variation of liquid film bearing capacity with the number of grooves(a)，spiral angle (b)，the groove depth ratio (c)，the circumferential groove platform ratio and the radial groove platform ratio(d)

从图6中可以看出，样机液膜摩擦转矩随槽数和螺旋角的增大均呈现出先增大后减小的规律，随槽深比的增大呈现出逐渐减小的规律，随槽台比和槽坝比的增大均呈现出逐渐减小的规律。

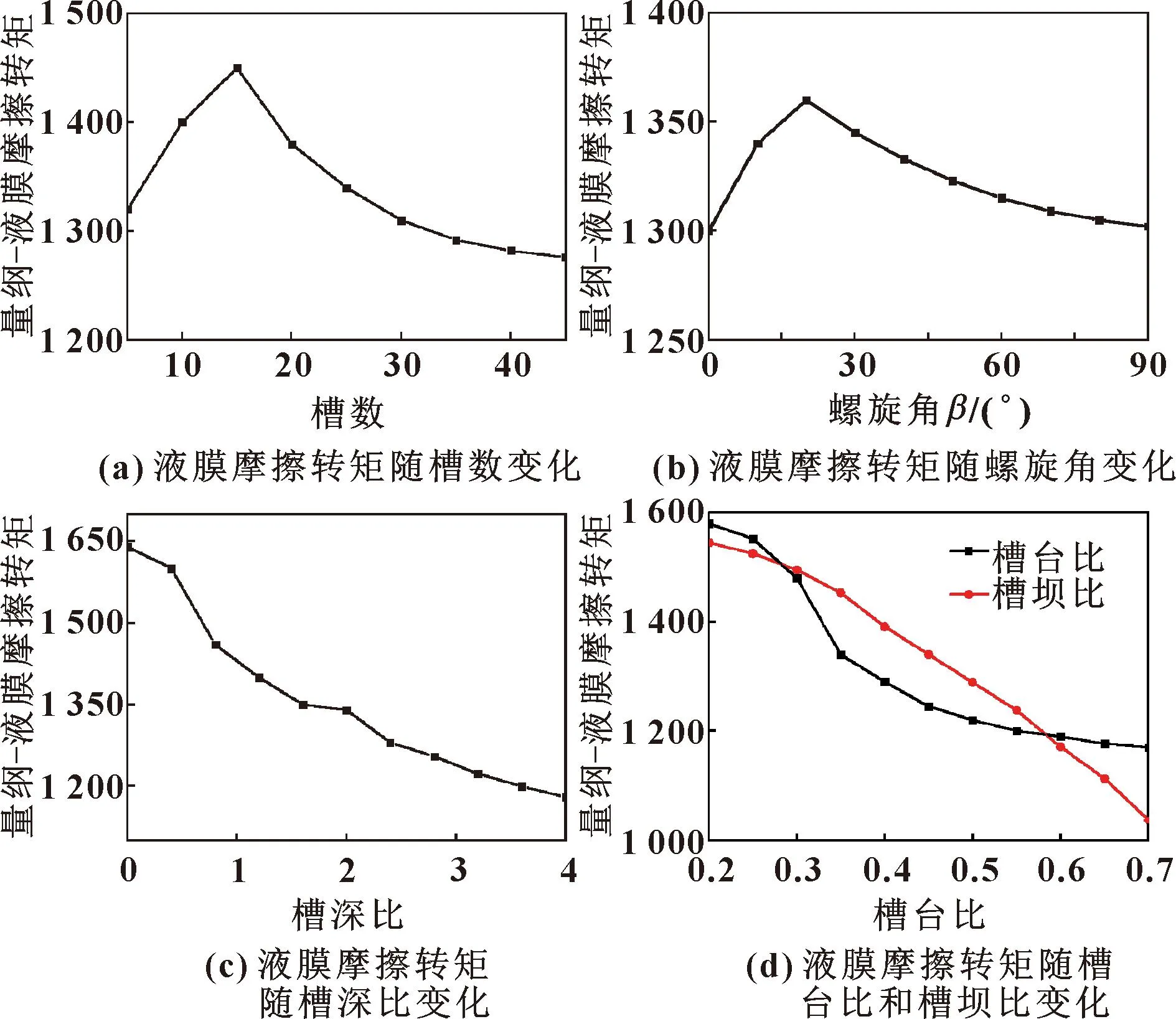
图6 液膜摩擦转矩随槽数、螺旋角、槽深比、槽台比 和槽坝比变化Fig.6 Variation of liquid film friction torque with the number of grooves(a)，spiral angle (b)，the groove depth ratio (c)，the circumferential groove platform ratio and the radial groove platform ratio(d)

综合来看，槽数、螺旋角、槽深比、槽台比和径向槽台比通过合理组合，才能使得液膜承载力较大、泄漏量适中、摩擦转矩较小，兼顾密封装置的稳定性、密封性和开启性能。为实现上述目标，各参数优选范围为：螺旋角β=10°～45°，槽数Ng=10～45，槽深比Δ=0.8～3，槽台比δθ=0.2～0.6，径向槽台比δr=0.2～0.6。为叙述方便，下文均称螺旋槽式旋转隔壁密封装置为螺旋槽密封装置。

3 螺旋槽密封参数优化设计

3.1 优化方案设计

以螺旋槽密封装置泄漏量为响应值，根据图4—6分析结果，选取对响应值影响效果显著的5个因素分别为：螺旋角A、槽数B、槽深比C、槽台比D和槽坝比E，试验设计了5因素及3水平如表1所示。为兼顾密封装置稳定性、开启性能和密封性能等，这5个因素取值范围根据理论分析的优选范围，其他试验样机参数取值和计算模型一致，试验中，槽深比根据调整密封结构闭合力逐步调整到位。采用Box-Behnken响应面设计法对螺旋槽密封装置密封性能进行试验设计，根据试验获得的样本数据通过多元二次回归方程拟合各因素与响应值间的函数关系，以此预测多变量下的最优响应值及寻找最佳试验条件。

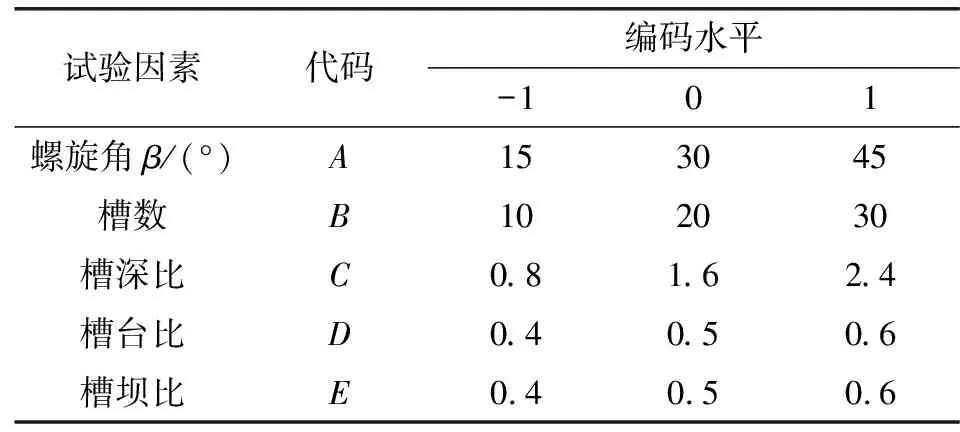
表1 Box-Behnken试验因素范围和水平

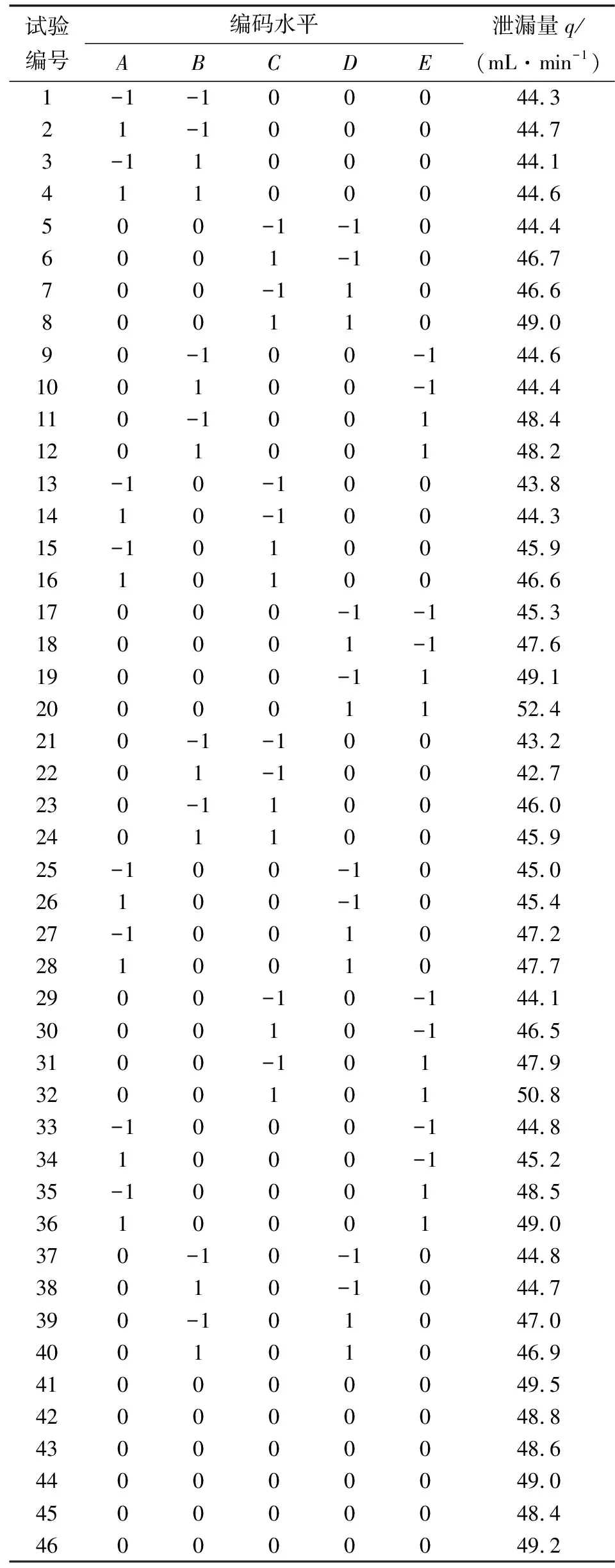
表2 试验方案及结果

3.2 试验结果及分析

3.2.1 回归分析与模型建立

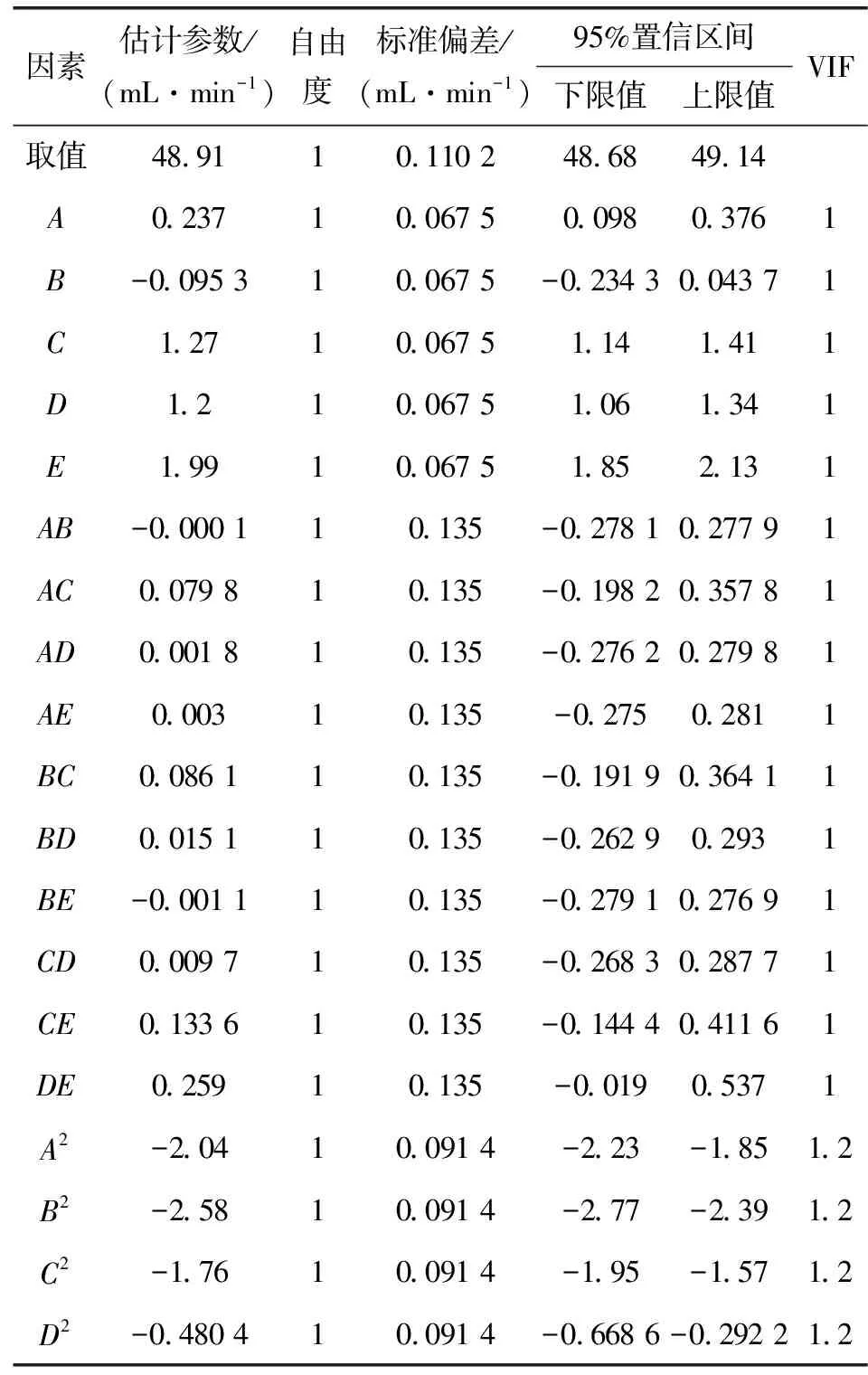
表3给出了多种模型方差分析的结果，其中F值是用于对模型显著性的检验，p代表了显著性水平，p>0.05则表示模型不显著。表4给出了多种模型R2值综合分析结果，R2表征了数学模型对试验数据的拟合程度，其值越接近于1说明模型拟合越好。表5给出了二次方数学模型方程参数估计和置信度分析结果，VIF是变量膨胀因子用于表征多重共线性，其值在0～10之间表示可接受。结合表3—5多种模型参数对比结果，只有二次方程数学模型满足p<0.05，且R2为0.991 5远大于0.95；此外R2校正值为0.984 7和预测值0.975 1接近，说明预测结果和试验结果相关性较强、拟合度较高，二次方程数学模型可用于分析和预测螺旋槽密封装置泄漏量的试验结果；另外方程中A、B、C、D和E5个因素的一次项和二次项对响应值影响显著，二次交互项对响应值也有一定的影响，说明各因素与螺旋槽密封装置泄漏量之间不是简单的线性关系；从影响显著程度来看，一次项E>C>D>A>B，二次交互项DE>CE>BC>AC>BD>CD>AE>AD>BE>AB，二次项B2>A2>C2>D2，且二次项的影响强于一次项，一次项的影响普遍强于二次交互项，二次交互项中DE和CE对响应值的影响较大，AE、AD、BE和AB对响应值的影响较小。

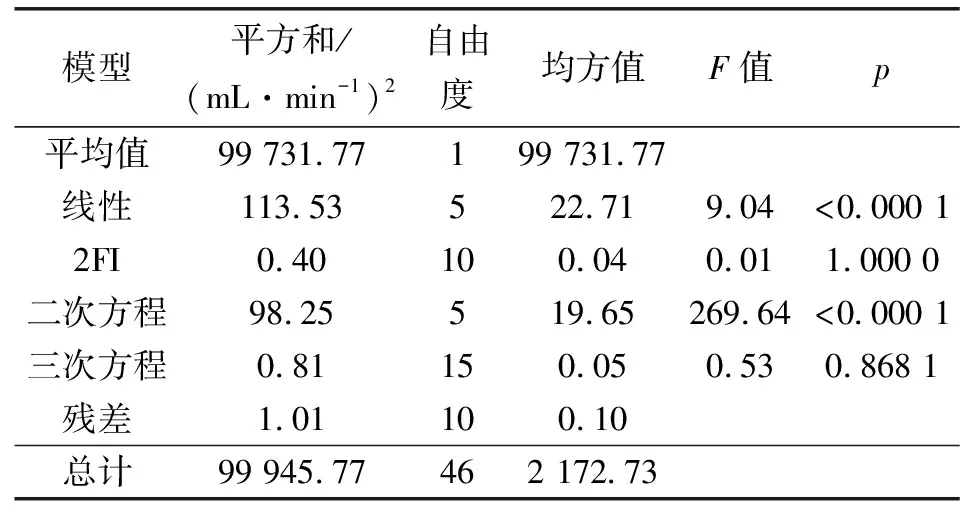
表3 多模型方差分析对比

表4 R2综合分析对比

以编码水平作为因素取值范围，泄漏量作为响应值进行响应面分析，泄漏量回归方程为

Y=48.91+0.237A-0.095 3B+1.27C+1.2D+

1.99E-0.000 1AB+0.079 8AC+0.001 8AD+

0.003AE+0.086 1BC+0.015 1BD-0.001 1BE+

0.009 7CD+0.133 6CE+0.259DE-2.04A2-

2.58B2-1.76C2-0.480 4D2

3.2.2 泄漏量影响因素分析

图7所示为泄漏量回归方程(8)对应的二阶交互项三维响应曲面图和等高线图，反映了10个二阶交互项对螺旋槽密封装置泄漏量影响情况。响应面曲面倾斜度越大，因素对响应值的影响越显著；等高线图则反映了2个因素交互作用显著程度，响应面曲面倾斜度越大，等高线图颜色的变化越快，沿变量方向高度差越大，该变量对响应值的影响越显著。

(8)

图7(a)所示是螺旋角A和槽数B交互作用下三维响应曲面图和等高线图。可以看出，随着螺旋角和槽数增大，泄漏量均呈现出先增大后减小的趋势，且沿2个变量方向变化趋势均较为明显；螺旋角在15°～45°范围内变化、槽数在10～30范围内变化时，泄漏量在44.1～49.5 mL/min范围内变化；当螺旋角和槽数处于核心区域的椭圆约束范围内时，泄漏量大于48 mL/min；当螺旋角取值15°、槽数为30时，泄漏量取值较小为44.1 mL/min。当螺旋角小于10°或大于45°时，泄漏量继续减小，假设螺旋角为0°，即无螺旋时，泄漏量较低，但结合图5、6，此时将导致螺旋槽密封装置的液膜摩擦转矩和液膜承载力大幅降低。

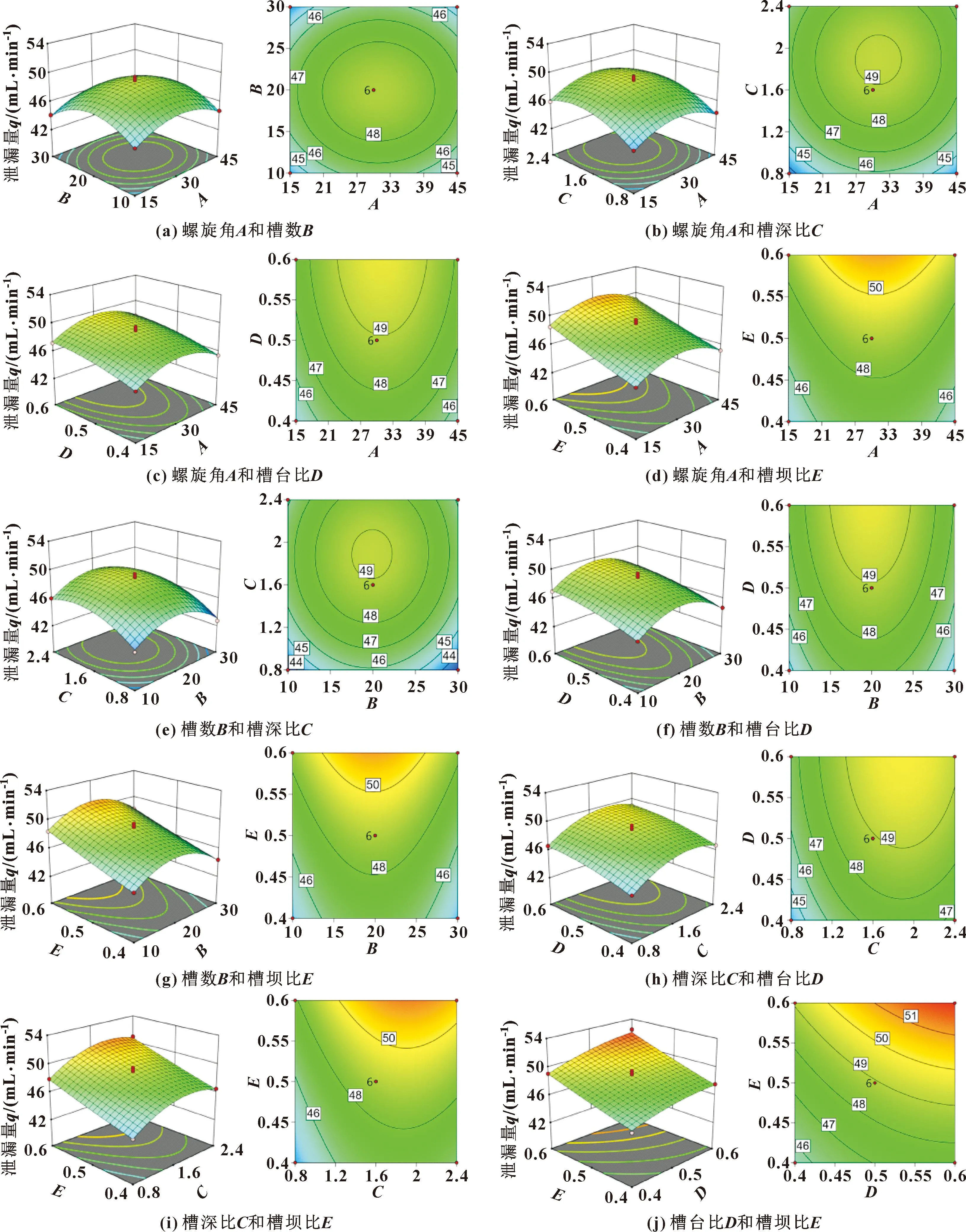
图7 二阶交互项响应曲面图和等高线图Fig.7 Response surface and contour map of second-order interaction term：(a)helix angle A and groove number B；(b)helix angle Aand groove depth ratio C；(c)helix angle A and circumferential groove platform ratio D；(d)helix angle A and radial groove platform ratio E；(e)groove number B and groove depth ratio C；(f)groove number B and circumferential groove platform ratio D； (g)groove number B and radial groove platform ratio E； (h)groove depth ratio C and circumferential groove platform ratio D；(i) groove depth ratio C and radial groove platform ratio E；(j)circumferential groove platform ratio D and radial groove platform ratio E

图7(b)所示是螺旋角A和槽深比C交互作用下三维响应曲面图和等高线图。随着螺旋角和槽深比的增加，泄漏量同样呈现出先增大后减小的趋势；螺旋角在15°～45°范围内变化、槽深比在0.8～2.4范围内变化时，泄漏量在43.8～49.2 mL/min范围内变化；当螺旋角和槽深比处于核心区域的椭圆约束范围内时，泄漏量大于49 mL/min；当螺旋角和槽深比分别取值15°和0.8时，泄漏量为43.8 mL/min。当槽深比小于0.8时，泄漏量继续降低，假设槽深比为0，即无凹槽，泄漏量较低，但结合图5、6，此时将导致螺旋槽密封装置液膜承载力大幅降低，液膜摩擦转矩大幅增加。

图7(c)所示是螺旋角A和槽台比D交互作用下三维响应曲面图和等高线图。可以看出，随着螺旋角和槽台比的增大，泄漏量均呈现出先增大后减小的趋势，且沿2个变量方向变化趋势差别较大；螺旋角在15°～45°范围内变化、槽台比在0.4～0.6范围内变化时，泄漏量在45.0～49.6 mL/min范围内变化；核心区域即椭圆中心只有在槽台比大于0.6时才会出现，当螺旋角和槽台比分别取值15°和0.4时，泄漏量较小为45.0 mL/min。假设槽台比接近0，即槽台极窄，结合图5、6可知，此时泄漏量较低，但将导致螺旋槽密封装置液膜承载力大幅降低、液膜摩擦转矩大幅增加。

图7(d)所示是螺旋角A和槽坝比E交互作用三维响应曲面图和等高线图。可以看出，随着螺旋角和的槽台比增大，泄漏量均呈现出先增大后减小的趋势，这是由于沿2个变量方向变化趋势快慢差别较大导致；螺旋角在15°～45°范围内变化、槽坝比在0.4～0.6范围内变化时，泄漏量在44.8～51.0 mL/min范围内变化。当周向槽台比取较小值时，有利于降低泄漏量。假设槽坝比接近于0，即槽台极矮，结合图5、6可知，此时泄漏量较低，但同样将导致螺旋槽密封装置液膜承载力大幅降低、液膜摩擦转矩大幅增加。

同样地，其他二次交互项泄漏量变化趋势均有以上类似的规律。综合来看，二次交互项中主要是DE和CE对响应值的影响较大。其中DE的等高线图核心区域的椭圆形状呈现旋转的特点，结合泄漏量回归方程(8)可以给出解释：当方程只有2项因素为变量其他项取定值时，回归方程可简化为椭圆函数，由于函数方程中同时存在交互项和一次项，而交互项和一次项的常系数又较大，这导致椭圆函数的长轴和短轴不再沿着横轴和纵轴，而是产生了较大的旋转，且旋转的角度也可根据方程求出。结合图4—6分析结果，说明螺旋角、槽数、槽深比、槽台比和径向槽台比通过合理组合，有利于密封液膜的有效建立，使得螺旋槽旋转密封装置具有优良的密封性能。

通过内学生化残差绘制螺旋槽密封装置泄漏量预测值与实际值对比如图8所示，用以进一步验证选取数学模型的准确度。可见，数据点分布在一条直线附近，说明预测模型可靠。

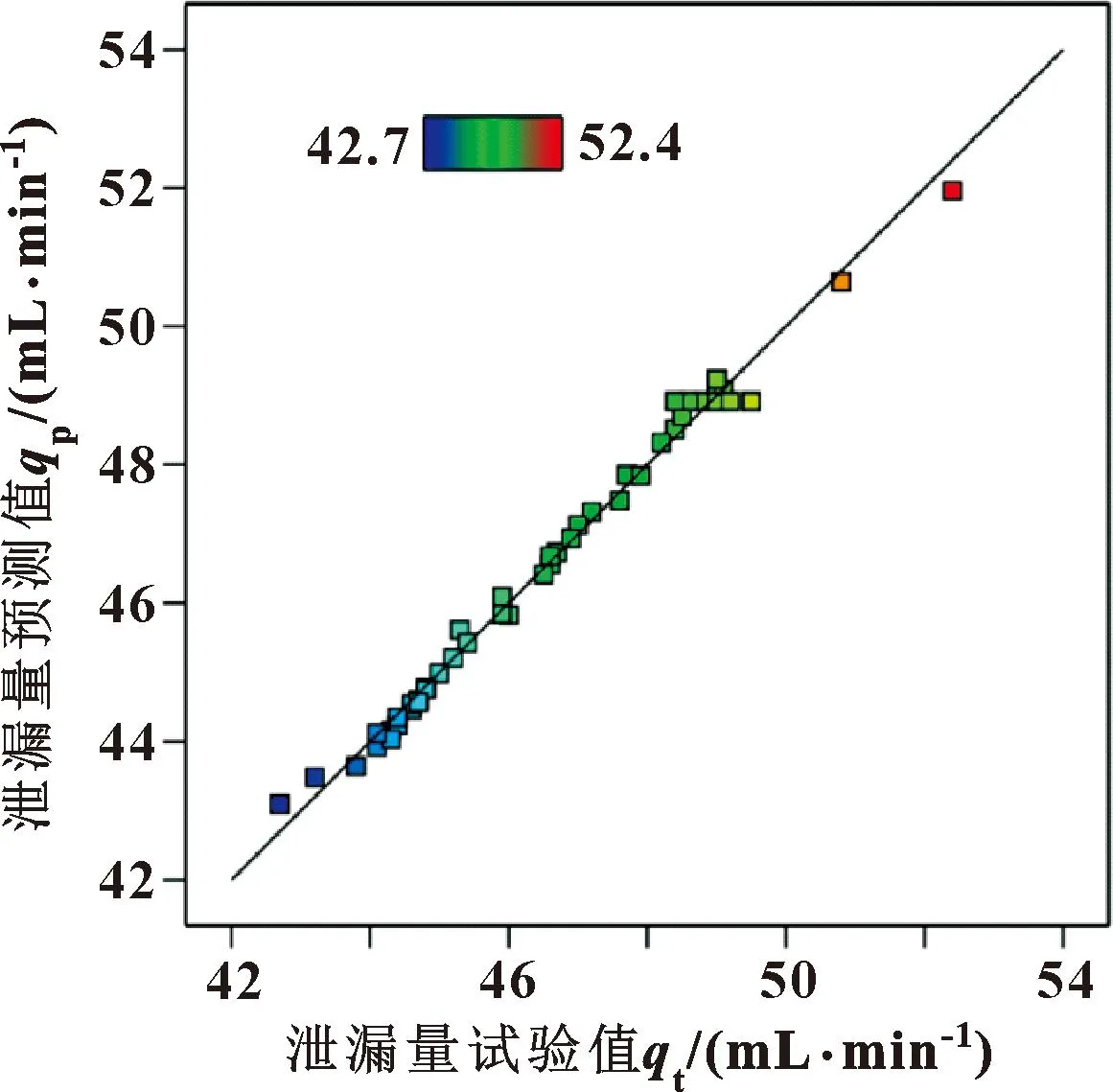
图8 泄漏量预测值与实际值对比Fig.8 Comparison between predicted values and actual values of leakage

3.2.3 最优化试验条件及试验验证

每个因素根据实际取值范围取值，将螺旋槽密封装置泄漏量最小值作为优化指标，选用numerical(愿望函数)数字化方法进行优化，由愿望函数优化出的最佳取值为：螺旋角A=17°，槽数B=26，槽深比C=0.84，槽台比D=0.32，槽坝比E=0.38，螺旋槽密封装置泄漏量为37.8 mL/min。此时最优方案在参数的优选范围内，说明最优方案的液膜承载力较大、摩擦转矩较小，在兼顾螺旋槽密封装置密封性能时，密封环开启性与稳定性也得到了较好的保障。表2中46组试验未包含numerical优化方法给出的最佳试验方案，为进一步验证预测模型的准确性，根据最优方案制造的试验样机进行了泄漏量测试，泄漏量试验值为38.4 mL/min，与最优化设计的预测值37.8 mL/min相差1.6%，这表明试验结果和预测结果一致，说明建立的螺旋槽密封装置泄漏量数学模型准确可靠，该模型可用于准确预测该类船用螺旋槽密封装置泄漏量。

3.2.4 最优范围遗传算法优化

在实际工程中，密封装置泄漏量在取最小值的基础上小幅度增大同样能满足使用要求。针对numerical(愿望函数)优化得到的螺旋槽参数最优解，文中利用Matlab工具箱中的遗传算法进行优化求解，遗传算法选取公式(8)作为个体的适应度函数，求取螺旋槽参数优化范围。遗传算法优化计算流程见图9。

图9 遗传算法优化流程Fig.9 Genetic algorithm optimization flow

具体计算步骤：

(1)初始化设置：设置进化迭代数计数器初始值为t=0，最大迭代数为G，随机生成N个个体作为初始值P(0)。

(2)个体评价：计算群体P(t)中各个体的适应度，文中选取式(8)作为个体适应度函数。

(3)选择运算：将选择算子作用于群体，根据个体适应度，选择一些优良个体遗传到下一代群体。

(4)交叉运算：将交叉算子作用于群体，对选中的成对个体，以某一概率交换它们之间的部分染色体，产生新的个体。

(5)变异运算：将变异算子作用于群体，通过带有猜测性质的3种运算将群体P(t)推进到下一代群体P(t+1)。

(6)终止条件判断：若t≤G，则t=t+1，并计算群体P(t+1)中各个体的适应度，若t>G，则终止计算，选取上述计算过程中最大适应度的个体作为最优解。

若以不超出numerical方法得到的泄漏量最优值15%作为密封装置可接受的泄漏量范围，以泄漏量回归方程(8)作为优化约束条件，最终终止判断条件变为，群体P(t)中个体的适应度满足约束条件，并记录其中具有最大适应度的个体，优化约束不等式方程为

Y=48.91+0.237A-0.095 3B+1.27C+1.2D+

1.99E-0.000 1AB+0.079 8AC+0.001 8AD+

0.003AE+0.086 1BC+0.015 1BD-0.001 1BE+

0.009 7CD+0.133 6CE+0.259DE-2.04A2-2.58B2-

1.76C2-0.480 4D2-37.8≤ 37.8×15%

(9)

通过遗传算法迭代计算，得到螺旋槽参数优化范围为：螺旋角β=15°～25°，槽数Ng=23～29，槽深比Δ=0.63～1.4，槽台比δθ=0.22～0.38，径向槽台比δr=0.27～0.44。虽然遗传算法个体的适应度函数只有泄漏量，但理论优选的范围则兼顾了密封装置的其他密封性能，将遗传算法优化范围和理论方法的优选范围求交集，即通过响应面试验、遗传算法和理论方法相结合的方法获取的密封装置螺旋槽参数最优范围应为：螺旋角β=15°～25°，槽数Ng=23～29，槽深比Δ=0.8～1.4，槽台比δθ=0.22～0.38，径向槽台比δr=0.27～0.44。

4 结论

(1)螺旋槽密封装置泄漏量随槽数、螺旋角和槽深比的增大均呈现出先增大后减小的规律，随槽台比和槽坝比的增大则呈现出逐渐增大的规律。泄漏量降低的同时，往往也导致液膜承载力降低，液膜摩擦转矩增加，参数选取合适范围时，螺旋槽密封装置可兼顾密封性、开启性和稳定性等。

(2)通过回归方程分析，得到了各因素对泄漏量响应值显著性程度结果。其中，二次项的影响强于一次项，一次项的影响普遍强于二次交互项，二次交互项中槽台比和槽坝比、槽深比和槽坝比对响应值的影响较大，螺旋角和槽坝比、螺旋角和槽台比、槽数和槽坝比、螺旋角和槽数对响应值的影响较小。

(3)将响应面试验设计法、遗传算法和理论方法3种方法相结合研究螺旋槽密封性能，可快速准确地获得螺旋槽参数最优取值范围。