燕尾静压导轨初始油膜厚度对静动态性能的影响

韩彦伟，李辉，赵玉博

(中国航空制造技术研究院，北京 100024)

闭式静压导轨具有阻力小、运动精度高、抗振动能力好等显著优点，目前已广泛应用于精密、重载的加工机床[1-5]。对于闭式静压导轨的研究，目前国内外主要集中于导轨配置的节流器参数、导轨工作时的受力变形等因素对导轨产生的影响[6]。施晨淳等[7]通过对四油垫闭式液体建立准静态理论模型，分析了PM流量控制器的参数变动对其运动精度的影响，为相应类型导轨的PM流量控制器参数选型提供了参考；王炯琨等[3]通过ANSYS/Fluent软件，分析了基于小孔节流器的闭式液体静压导轨的流场分布规律和承载特性，获得了流场分布规律的关键物理参数，为优化导轨结构提供了参考。赵建华和高殿荣[8]研究了传统闭式液体静压导轨在不同油膜厚度的工作性能，得出了其在较低油膜厚度时有着更好工作效率的结论。

然而以上对闭式静压导轨的研究都做了一定简化处理，将所研究对象的初始条件都设为默认值，且忽略了闭式静压导轨初始参数对其工作性能的影响，以及静压导轨未加负载时达到自我平衡的过程；另外，研究范畴都局限于传统闭式静压导轨，未将研究对象扩展到闭式静压导轨的衍生类型，例如燕尾静压导轨等。本文作者惟燕尾静压导轨为例，分析了静压导轨设计参数之一的初始油膜厚度取值对导轨工作性能的影响。

1 燕尾静压导轨

1.1 燕尾静压导轨工作原理

燕尾静压导轨是一种新型的闭式静压导轨，导轨整体呈燕尾形，用于提供静压力的油垫分别布置于导轨的燕尾面与底层大面(后文简称为大面)，其简易模型及工作原理示意图如图1所示。

图1 燕尾静压导轨模型及工作原理Fig.1 Dovetail hydrostatic guide model and working principle： (a)simple model；(b)schematic of the working principle

在燕尾静压导轨的设计中，可以根据不同的工作要求，将大面与燕尾面之间设计成不同的角度，文中模型将其设置为60°。

燕尾静压导轨工作时，油垫与导轨之间存在一层液压油膜。当导轨承受负载发生变化时，油膜厚度会相应变化，改变油垫通过油膜向导轨提供的静压力，直到与外载荷相平衡。其流量-压力公式[9]如式(1)所示。根据式(1)可知油垫通过油膜向导轨提供的静压力pr大小与液阻及流过油垫的液压油流量直接相关。

pr=qR

(1)

式中：q为流过油垫的流量，与导轨所匹配的流量控制器相关；R为液阻，受油垫的尺寸、液压油的种类以及油膜厚度等因素影响，具体计算公式如公式(2)所示[10]。

(2)

式中：μ是液压油在工况下的动力黏度，受液压油的种类及工作温度影响；δ是油垫某个时刻的油膜厚度；B、L、b1、l1则是油垫的结构设计参数。

导轨受到的外载荷增大时，大面油垫油膜会逐渐被压缩，而燕尾面油垫油膜厚度则会逐渐增加，改变油垫向外提供的静压力，直到与外载荷相平衡，如图2所示。

图2 加载前后油膜厚度变化示意Fig.2 Schematic of changes in oil film thickness before and after loading：(a) before loading；(b)after loading

图中h1、h2分别为大面油垫与导轨、燕尾面油垫与导轨之间的油膜厚度。燕尾面与大面夹角为60°，通过对运动进行分解，导轨向下位移量为h时，大面油膜厚度压缩量Δh1、燕尾面油膜厚度增大量Δh2具有以下关系：

2Δh2=Δh1=h

(3)

1.2 油垫及流量控制器

油垫是导轨用来提供静压力的元器件，由油腔、进油孔与封油边等部分组成[11]，如图3所示，文中采用的油垫参数见表1。

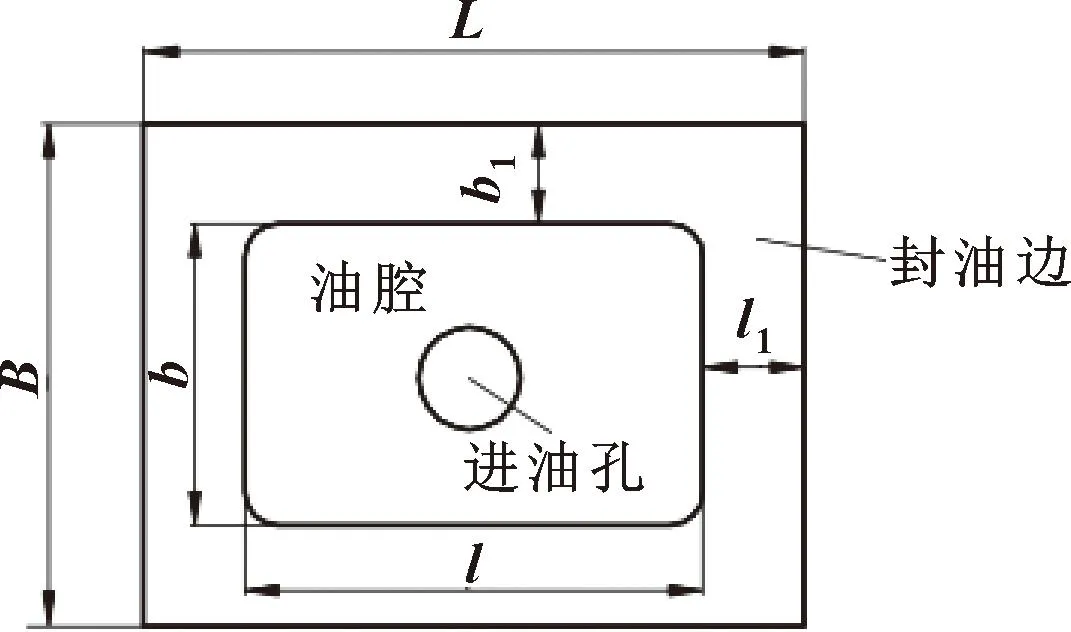
图3 油垫结构示意Fig.3 Schematic of oil pad structure

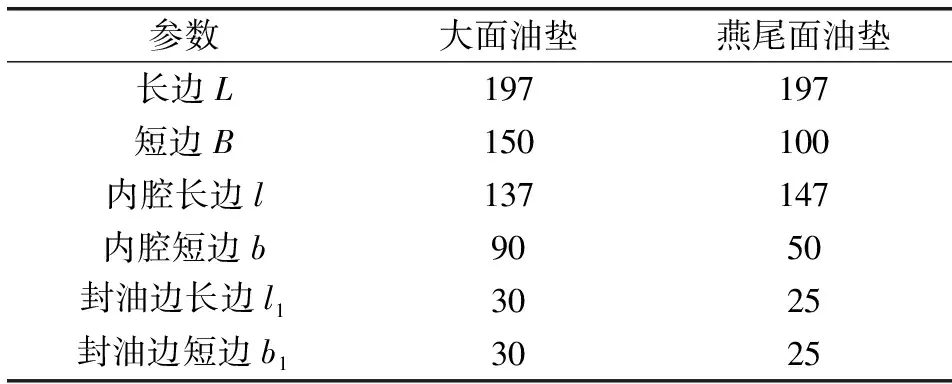
表1 油垫尺寸单位：mm

流量控制器是静压导轨用于调节输出压力的元器件，文中选用PM流量控制器——一种可变式的单面薄膜反馈流量控制器，其压力-流量特性方程[12]如公式(4)所示。

qr(pr)=q0[1+(Kr-1)pr/ps]

(4)

式中：pr为油腔压力值；q0为PM流量控制器的初始流量值；ps为供油压力；Kr为比流量，以上参数皆为PM流量控制器设计参数，选型之后皆为定值；qr为油腔压力输出流量。

选取的PM流量控制器主要参数为：初始流量q0=75 mL/min(对应于油液动力黏度μ=10 mPa·s)，供油压力ps=16 MPa，比流量Kr=2.8。

公式(4)中流量是以选取液压油动力黏度为10 mPa·s时进行计算的，当实际工况下液压油的动力黏度不为10 mPa·s时，可以按照公式(2)进行换算。

qn=(10q10)/μn

(5)

文中所选取工作温度为25 ℃，在该温度下液压油动力黏度为173 mPa·s。

根据公式(1)、(2)、(4)可以得出基于PM流量控制器的燕尾静压导轨，大面与燕尾面的油腔压力为

(6)

其中Cr计算如公式(7)所示，该参数只与油垫自身的设计尺寸及静压导轨所使用液压油黏度相关，在恒温工况下为定值，不受载荷及油膜厚度变动影响。

(7)

2 油膜初始厚度对导轨性能的影响

燕尾导轨的工作性能分类为静态性能和动态性能。静态性能是指导轨在外负载不再变化时，导轨表现出的性能，主要是指导轨的承载力和刚度；而动态性能是指导轨在承受负载开始振动，到系统达到稳定这一过程中表现出的性能[13]。

2.1 静态性能

如图4所示，当导轨承受负载时，由大面与燕尾面油垫提供的静压力共同平衡施加在导轨上的负载。

图4 静压导轨受力示意Fig.4 Schematic of the force of the static pressure guide rail

将燕尾面油垫提供的静压力分解为与大面静压力同向的分力和垂直于大面受力方向的分力，如图5所示。F1、F2分别为大面与燕尾面油腔提供的静压力，F2x、F2y则是燕尾面油腔提供静压力的分力，大小为

(8)

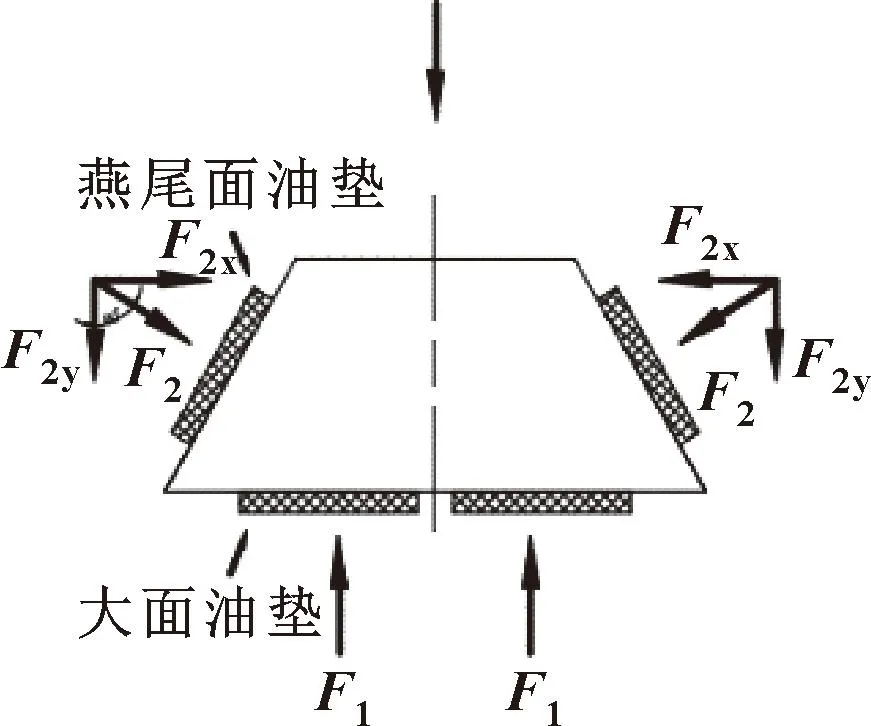
图5 受力分解示意Fig.5 Schematic of force decomposition

由于油垫是对称布置，假设加载时不会发生偏载，则近似认为燕尾面布置的任一静压油腔的静压力分力F2y都会与对称燕尾面油腔的静压力分力F2y相互抵消。将相邻位置的燕尾面油垫与大面油垫分为一组，每组油垫承载的负载为

F=F1-F2x=pr1Ae1-0.5pr2Ae2=

(9)

其中Ae为油垫的有效承载面积，只受油垫自身的设计尺寸限制，具体计算公式如公式(10)所示[14]。

Ae=1/4(L+l)(B+b)

(10)

初始状态下，导轨未承受外载荷，此时大面与燕尾面油垫会根据所设置的初始油膜厚度h01、h02提供一定的静压力，但这些静压力未必会使导轨正好受力平衡。在系统的调节下，导轨会发生一定位移x改变油垫的油膜厚度，使导轨达到受力平衡(x可以通过公式(11)求得，且为唯一解)。令此时的油膜厚度为h10、h20，建立力学平衡方程如公式(12)所示。

h10=h01-x，h20=h02+0.5x

(11)

0=pr1，0Ae1-0.5pr2，0Ae2

(12)

其中：pr1，0与pr2，0分别为导轨在初始状态下调节至平衡时大面与燕尾面油垫油腔的压力值。

2.1.1 最大承载能力

随着负载的不断增大，大面油垫油膜会不断压缩，燕尾面油垫油膜厚度则会不断增大，当大面的油膜厚度被压缩到最小值时，燕尾面油膜厚度会达到最大值，此时燕尾导轨达到理论最大承载能力。根据公式(9)可以得出，当油垫尺寸、PM流量控制器参数、工况温度为确定值时，每组油垫的最大承载能力只与燕尾导轨初始油膜厚度相关。考虑到PM流量控制器可提供的最大工作压力为供油压力的0.9倍[15]，即为0.9ps，则可推导出静压导轨每组油垫最大承载能力为

(13)

根据公式(13)绘制出最大承载力与燕尾导轨不同初始油膜厚度之间关系曲线图，如图6所示。

图6 最大承载力随初始油膜厚度的变化Fig.6 Variation of maximum bearing capacity with initial oil film thickness

大面与燕尾面油膜初始厚度取值皆为0.05 mm时，单对油垫最大承载力为280.6 kN；大面初始油膜厚度取值0.05 mm，燕尾面初始油膜厚度取值0.06 mm时，单对油垫最大承载力可以达到283.4 kN；大面初始油膜厚度取值0.06 mm，燕尾面初始油膜厚度取值0.05 mm时，单对油垫最大承载力可以达到282.2 kN。可知，随着燕尾导轨初始油膜厚度的增大，导轨的最大承载能力逐渐增大，相较于大面油垫，燕尾面油垫油膜初始厚度的变动对导轨最大承载能力有着更大的影响。但从数值变化范围来看，初始油膜厚度的变化并不会引起导轨承载能力较大的波动。

2.1.2 静刚度

静刚度是描述导轨抵抗负载变动的能力，是静压导轨的一项重要性能指标，静刚度越大，导轨的稳定性越好，工作精度越高。燕尾导轨的静刚度可以定义为：在单位负载的变动下，导轨位移的变动量。单位载荷变动下导轨位移量越大，则静刚度越低；或者在导轨位移数值一定时，需要的载荷增大量越大，燕尾导轨刚度越高。

根据公式(3)与公式(9)可以得出单对油垫承担载荷为F时，与导轨位移量h之间具有以下关系：

(14)

通过计算，大面油膜初始厚度为0.06 mm，燕尾面初始油膜厚度为0.06 mm时，从燕尾导轨初始位置到向下平移10 μm时，每对油垫负载变化范围为40.3～118.5 kN，变化量为78.2 kN；大面油膜初始厚度为0.055 mm，从燕尾导轨初始位置向下平移10 μm时，每对油垫负载变化范围为60.8～235.5 kN，变化量为174.7 kN；大面油膜初始厚度为0.06 mm，燕尾面初始油膜厚度为0.055 mm时，从燕尾导轨初始位置向下平移10 μm时，每对油垫负载变化范围为32.7～113.8 kN，变化量为81.1 kN。

可知降低燕尾面初始油膜的厚度，可以有效提高导轨的静刚度。但从数值的变化范围看，相较于燕尾面油膜，大面油膜初始厚度的减小对静刚度的提升幅度会有更大。

2.2 动态性能

考虑燕尾导轨的惯性力，对导轨进行受力分析，建立力学平衡方程：

(15)

式中：m为燕尾导轨质量。

当导轨处于动载荷作用下时，静压油膜存在油膜挤压效应[11]，通过油腔的液压油流量应为油腔压力作用下排出的流量与导轨移动而挤压出的流量之和/差：

(16)

其中导轨移动而挤压油液的挤压面积Ab=lb。

根据公式(1)—(3)，公式(16)可以改写为

(17)

对公式(17)通过泰勒级数展开进行线性化处理，并省略去高阶项，可以将其化简为

(18)

其中pr1=pr1，0+Δpr1，pr2=pr2，0+Δpr2。

将公式(18)代入公式(17)得到：

(19)

用公式(15)减去公式(12)可以得到：

(20)

将公式(19)代入公式(18)可以得到：

(21)

将公式(21)整理合并为公式(22)。

(22)

其中c、k分别为

(23)

式(23)中变量有h10、h20、pr1，0、pr2，0，而这些变量在初始油膜厚度确定时，都不会再发生变化，即c、k将为定值。

在MATLAB的simulink 工具中，对燕尾导轨进行仿真，分析不同类型工况下导轨的动态性能。

对公式(22)进行改写：

(24)

根据公式(24)搭建相应的模型，如图7所示。

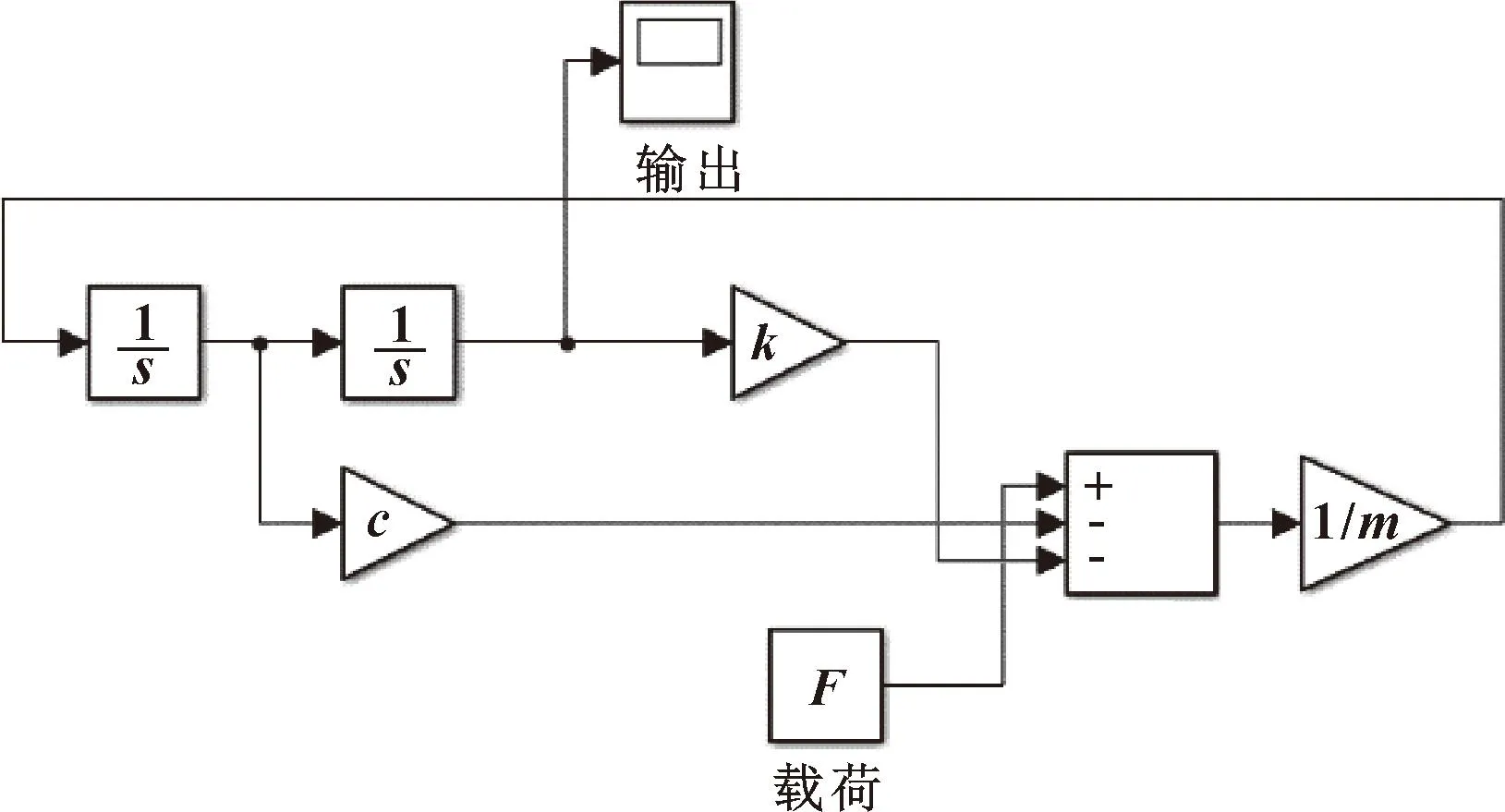
图7 Simulink仿真Fig.7 Simulink simulation

以某一燕尾的导轨工况参数为参考，模拟并比较该导轨在不同初始油膜厚度下的工作性能。

2.2.1 阶跃载荷下导轨动态性能

将未承担外载荷状态下的导轨短时间内施加压力至最大负载75 kN，近似看待为系统输入一个75 kN的阶跃载荷。

不同初始油膜厚度下燕尾导轨的振动曲线如图8所示。

从图8可以看出，在系统达到稳定前，曲线1与3的振动幅值皆大于曲线2，而曲线3幅值要大于曲线1。可以得出在阶跃载荷下曲线2代表的燕尾静压导轨的动刚度要大于其他两条曲线，即不论是燕尾静压导轨的大面还是燕尾面，增大初始油膜厚度均减小了导轨的动刚度，但燕尾面初始油膜厚度的变化对动刚度的影响更大。

图8 阶跃载荷下导轨动态性能Fig.8 Dynamic performance of guide under step load

2.2.2 周期性变动载荷下导轨动态性能

选取导轨的某一工况下需要承担50～70 kN的交变载荷。给予系统一个50～70 kN的周期性载荷，不同初始油膜厚度下燕尾导轨的振动曲线如图9所示。

从图9可以得出，处于交变载荷下燕尾静压导轨的性能与处于阶跃载荷下动态性能一致，不论是增大燕尾静压导轨大面还是燕尾面初始油膜厚度均减小了导轨的动刚度，但燕尾面初始油膜的变动对动刚度影响更大。

图9 交变载荷下导轨动态性能Fig.8 Dynamic performance of guide under alternating load

3 结论

(1)燕尾静压导轨油垫初始油膜厚度的选取与静压导轨最大承载能力相关，增大燕尾导轨初始油膜厚度，可以提高最大承载能力，但提升幅度不大。

(2)降低燕尾导轨初始油膜厚度，可以有效提高导轨系统的静、动态刚度。其中减小导轨底层大面油膜厚度对导轨静刚度的提升更大，而减小燕尾面初始油膜厚度则对导轨动刚度的提升更大。因此，导轨初始油膜厚度应根据实际工况选取，如果导轨在工况下大部分时间只需要承担固定载荷，应优先保证导轨底层大面选取较小的初始油膜厚度；如果导轨在工况下大部分时间需要承担的载荷处于变化状态，应优先保证燕尾面面选取较小的初始油膜厚度。