仿壁虎微黏附阵列负压流场数值模拟及试验研究

邱海飞，张嘉友，李成创，武振阳，王超辉，许昊

(西京学院机械工程学院，陕西西安 710123)

壁虎是一种体型微小、反应机敏的爬行纲动物。在长期的进化和演变过程中，壁虎形成了自身所独有的生物学特征和环境适应能力。相对于其他爬行纲动物，壁虎在三维空间具有十分突出的机动攀爬能力，可轻松活动于陡壁、悬崖、天花板及屋檐缝隙等险峻环境[1]。因此，以壁虎为原型的仿生研究一直备受关注，尤其是在民用、军事及航天等领域，类壁虎仿生机器人的探索及新型材料开发，无疑具有非常可期的发展和应用前景。

目前，围绕爬壁虎的仿生研究主要分为黏附技术和移动方式2个方向，其中，移动方式基本都以传动机械或机构为主，如车轮式、导轨式、履带式、腿足式及混合式等。黏附技术在很大程度上决定了仿生机体的攀爬性能，常见的黏附技术有磁吸附、静电吸附、负压吸附及化学黏附等[2]。由于微观机制的复杂性和仿生学层面的实现难度，长期以来，针对壁虎黏附阵列的科学探究，一直是爬壁仿生机器人发展的重中之重。

国外在壁虎黏附阵列仿生研究方面起步较早，迄今已取得多项实用性成果[3]，例如：美国斯坦福大学的研究人员研发了一种具有脚掌刚毛特征的黏附阵列，并在仿壁虎爬壁机器人上取得了良好应用效果；卡内基梅隆大学的研究人员通过注塑模加工和光刻工艺，制备获得了长径比为2.4～4的微米级黏附阵列，并在玻璃球面上对其进行了黏附性能测试；德国马普金属研究所的研究人员以硅橡胶为浇注材料，利用模具注塑法成功制备了长度为100 μm、直径为40 μm的微黏附阵列，并通过玻璃平面接触黏附测试得出其阵列的黏附强度超过光滑表面一倍；韩国的研究人员提出了一种具有多级分支结构和大长径比的微杆阵列制造方法，并通过模塑法获得了微米级聚合物阵列。

在国内，中科院合肥智能机械研究所以硅橡胶和聚酰亚胺为浇注材料，通过ICP 深刻蚀方法制备获得了具有多种长径比的微黏附阵列，并对其黏附性能进行了试验测试。此外，北京航空航天大学、哈尔滨工业大学、上海大学及中科院沈阳自动化所等，在爬壁仿生机器人和吸附技术探索方面也取得了一定进展，但总体上还与国外先进水平存在一定差距。

研究表明，不同黏附方式对于基底材料和所处环境都有相应要求，如磁吸附和静电吸附，要求接触壁面必须具有导磁性与导电性；化学黏附会因黏胶剂的挥发、固化而使黏附效果大受影响。相比之下，负压吸附不受壁面材质限制，而且可根据承载环境和基底特征调节吸力大小，具有相对较强的吸附稳定性和壁面适应性[4]，故而成为传统爬壁机器人常用的一种吸附方式。本文作者以爬壁虎为仿生原型，在结构分析、理论计算、CAD建模、有限元分析、CFD仿真及试验测试基础上，将一种基于负压控制的吸附方式应用于壁虎黏附阵列仿生研究，获得了可供实践参考的模拟和试验结果。

1 微黏阵列

壁虎之所以能够“飞檐走壁”，主要是因为其脚掌微观结构极为精细，如图1所示[5]，壁虎脚掌底部生长有数百万根极细刚毛，且每根刚毛末端又附着有400～1 000根长度约0.5 μm的绒毛分支(即微观黏附阵列)[6]。在这种特殊的脚掌绒毛阵列作用下，壁虎可与各种接触表面产生较大黏着力，即所谓的“范德华力”，是一种具有干性吸附特性的微弱电磁引力[7]。

图1 壁虎趾掌微观阵列[5]Fig.1 Micro array of gecko sole[5]

由于壁虎脚掌微观阵列具有黏附力强、脱附可控及环境适应性强等特点，所以其阵列结构和吸附机制一直是现代仿生技术关注的重点，特别是对于爬壁仿生机器人的发展及实践应用，具有重要的启发作用和现实研究意义。

2 负压的形成

为实现仿生壁虎的吸附与脱附动作，以真空吸盘替代壁虎脚掌，利用负压吸附方式模拟壁虎与壁面之间的接触黏着。根据负压物理特性及其形成机制，构建如图2所示气动控制回路，主要由真空发生器、软管、电磁阀、三通及吸盘等构成。

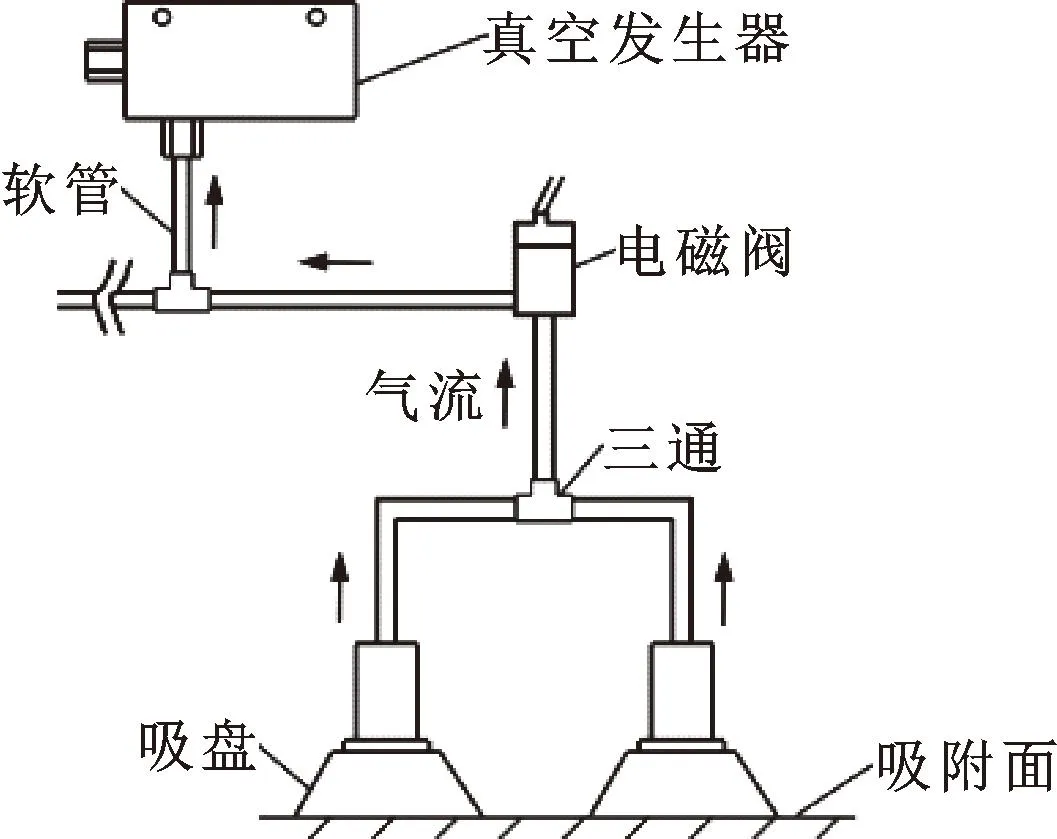
图2 负压气控回路Fig.2 Pneumatic control circuit of negative pressure

当仿生机体停留于垂直壁面时，电磁阀处于开启状态，此时真空发生器通过软管将吸盘内部空气抽走形成真空负压，而吸盘则在外部大气压力作用下被挤压吸附于壁面之上，此即负压吸附。而当需要使吸盘脱离壁面时，电磁阀在控制程序作用下关闭，真空发生器停止产生负压吸力，此时气动回路将与外部大气环境接通，使得吸盘内外压力大小相等，使得吸盘恢复原形而失去黏附能力。

3 壁面吸附力

3.1 吸盘结构

真空吸盘种类较多，常见的有扁平吸盘、波纹吸盘、椭圆吸盘及方形吸盘等[8]。考虑到壁面适应性和吸附负载等因素，仿生机体选用由硅胶材质制成的双层圆形波纹吸盘，如图3所示，该型吸盘高度H=26 mm，底部有效吸附直径d=33 mm，可通过上部连接管与气动回路装配相连。与普通吸盘相比，波纹吸盘具有较大的垂直变形压缩量，而且具备一定的摆动角度，可吸附于轻微斜面和较大弧度曲面。

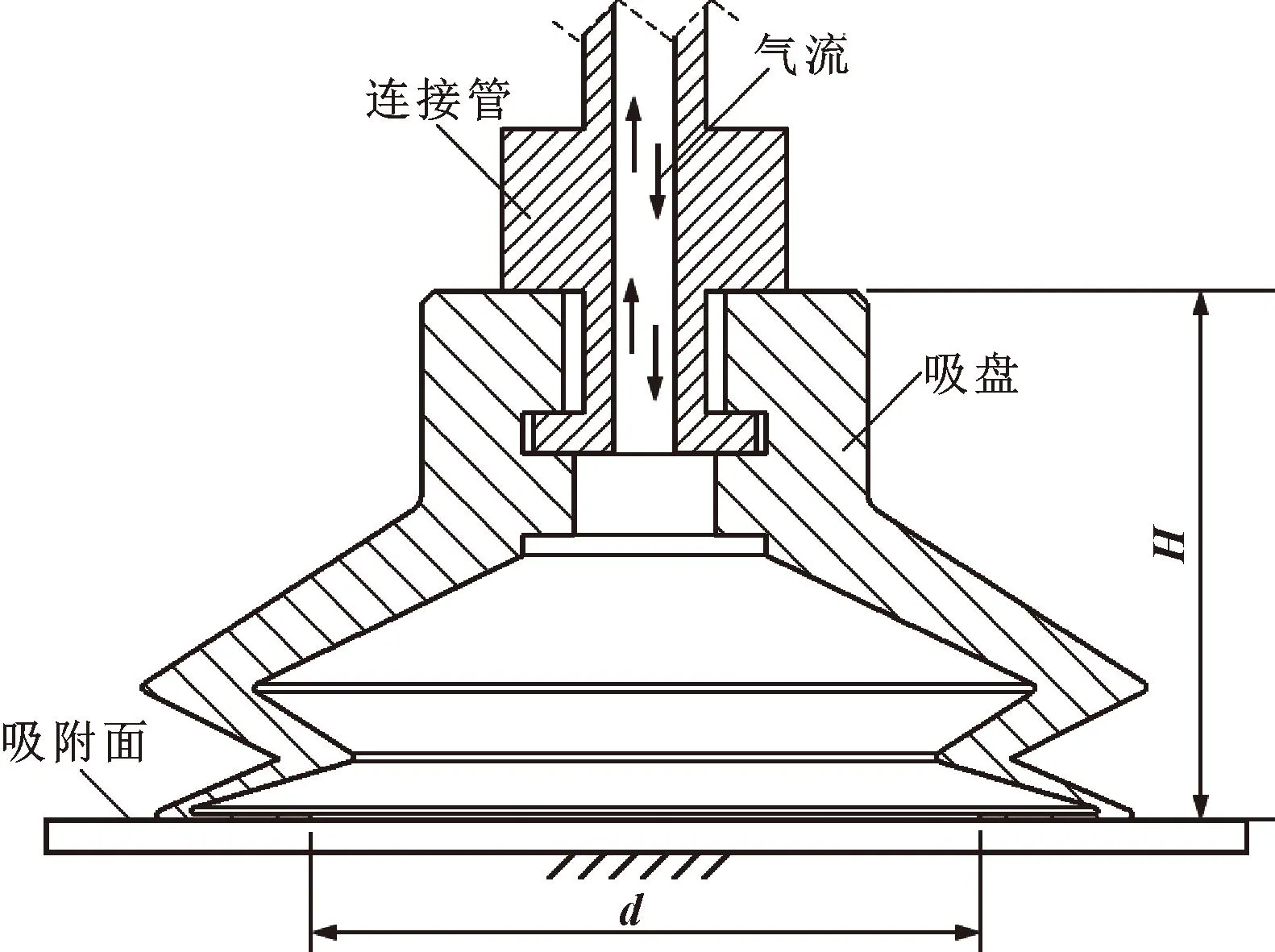
图3 吸盘剖面结构Fig.3 Section structure of suction cup

吸盘吸附效果与壁面形貌质量关系密切，在理想状态下，即当吸盘底部与光滑壁面接触时，会在壁面与盘体内部之间形成一个封闭腔体，此时吸附黏着力最强。若接触壁面较为粗糙，则会因为外部空气泄漏进入腔体而使内部压力降低，影响到吸附稳定性。

3.2 真空度分析

根据真空吸附相关理论，吸盘腔体内部真空度与抽气时间存在如下关系：

p=K1e-K2t+K3

(1)

式中：p为真空度；t为时间变量；K1、K2为真空发生器、容器体积、环境压力等相关常数；K3为极限真空度[9]。

显然，吸盘真空度p与抽气时间t成指数函数关系，说明抽气响应时间是决定吸盘能否迅速达到稳定吸附状态的重要因素。

当真空泵抽气开始后，随着时间推移，吸盘内部压力将按式(1)所示指数关系逐渐衰减。与此同时，吸盘内部真空度会随内压减小而增大，并将无限逼近真空发生器的最大真空度，直至腔体内真空度趋于稳定[10]，此时可按式(2)所示经验公式对真空度进行估算。

(2)

已知机体总质量m≈1.35 kg，重力加速度g=9.8 m/s2，则吸附载重Gm=13.23 N；吸盘有效吸附直径d=33 mm，吸盘数量n=4。考虑到吸附强度及稳定性，取安全系数f=10(水平吸附时f>4；垂直吸附时f>8)，将各参数值代入式(2)，计算得到吸盘所需理论真空度p≈38.69 kPa。为充分保证吸附安全性，实际搭建气动回路时选用负压p1=-55 kPa的真空发生器。

3.3 吸附力计算

当壁虎在垂直壁面吸附或攀爬时，为尽可能保持躯体平衡，至少应有两只脚掌同时与壁面接触[11]。由此可知，在垂直吸附承载状态下，如图4所示，要使仿生机体能够安全吸附于垂直壁面，就必须保证两只脚掌产生的黏附力大于等于机体自重Gm，即单个吸盘与壁面之间的最大静摩擦力Fmax应大于等于Gm/2(约6.62 N)，如式(3)所示。

(3)

图4 垂直吸附力学模型Fig.4 Mechanical model of vertical adsorption

在光滑垂直壁面上，吸盘吸附力W强弱主要取决于腔体实际真空度p1的大小[12]，两者之间的关系可用式(4)表示。

(4)

式中：S为有效吸附面积(πd2/4)；λ为安全系数(≥2.5)。

为增强安全设计裕度，令λ=3，并将其与p1和S的参数值一同代入式(4)，计算得到吸盘吸附力W=15.67 N。

吸附力W即为壁面受到的正压力，已知吸盘与壁面之间的最大静摩擦因数μ=0.55，则单个吸盘与壁面之间的最大静摩擦力Fmax≈8.62 N。

显然，Fmax>Gm/2，说明选用负压为-55 kPa的真空发生器，能够满足机体载重对于吸盘吸附力的要求。

4 流域建模与仿真

4.1 物理模型

根据真空吸盘工作环境和吸附特性，采用标准k-ε两方程模式构建其CFD流场物理模型。k-ε模式是工程流体计算中常用的标准湍流模型，由雷诺应力黏性模式可知，流场湍流涡黏度为湍动能与湍流耗散率的函数，如式(5)所示。

μt=Cμfμρk2/ε

(5)

式中：μt为湍流涡黏度；Cμ为经验常数；fμ为近壁衰减函数；ρ为流体密度；k为湍动能；ε为湍流耗散率。

标准k-ε模型假设流场状态为完全湍流，而且忽略分子黏性影响，其理论模型是一个半经验公式，主要求解湍动能输送方程和能量耗散方程，如式(6)和式(7)所示[13]。

(6)

(7)

式中：Gk为由层流速度梯度产生的湍动能；Gb为由浮力产生的湍动能；YM为可压缩流动中脉动扩张的贡献；C1ε、C2ε、C3ε为经验常数；σk、σε为k方程和ε方程的湍流Prandtl数；Sk、Sε为用户自定义源项。

当流场为不可压缩流动，且不考虑自定义源项时，可将方程模式中的常数项取值定义为：Gb=0；YM=0；Sk=0；Sε=0；C1ε=1.44；C2ε=1.92；C3ε=0.09；Cμ=1；σk=1；σε=1.3；σT=1；Pr=0.85。

4.2 流场网格离散

利用SolidWorks设计吸盘三维CAD实体模型，通过数据转换将其导入ICEM CFD中进行特征编辑和拓扑重构。采用非结构网格对流体计算域进行离散，如图5(a)、(b)所示，流场网格划分共产生1 738 083个单元和311 113个节点，主要以三角形单元和四面体单元为主。其中，网格大小介于0.22～1 mm之间，如图5(c)所示。可见流场中没有小于0.1 mm的网格，说明不存在负体积单元，网格扭曲度符合流场计算精度要求。

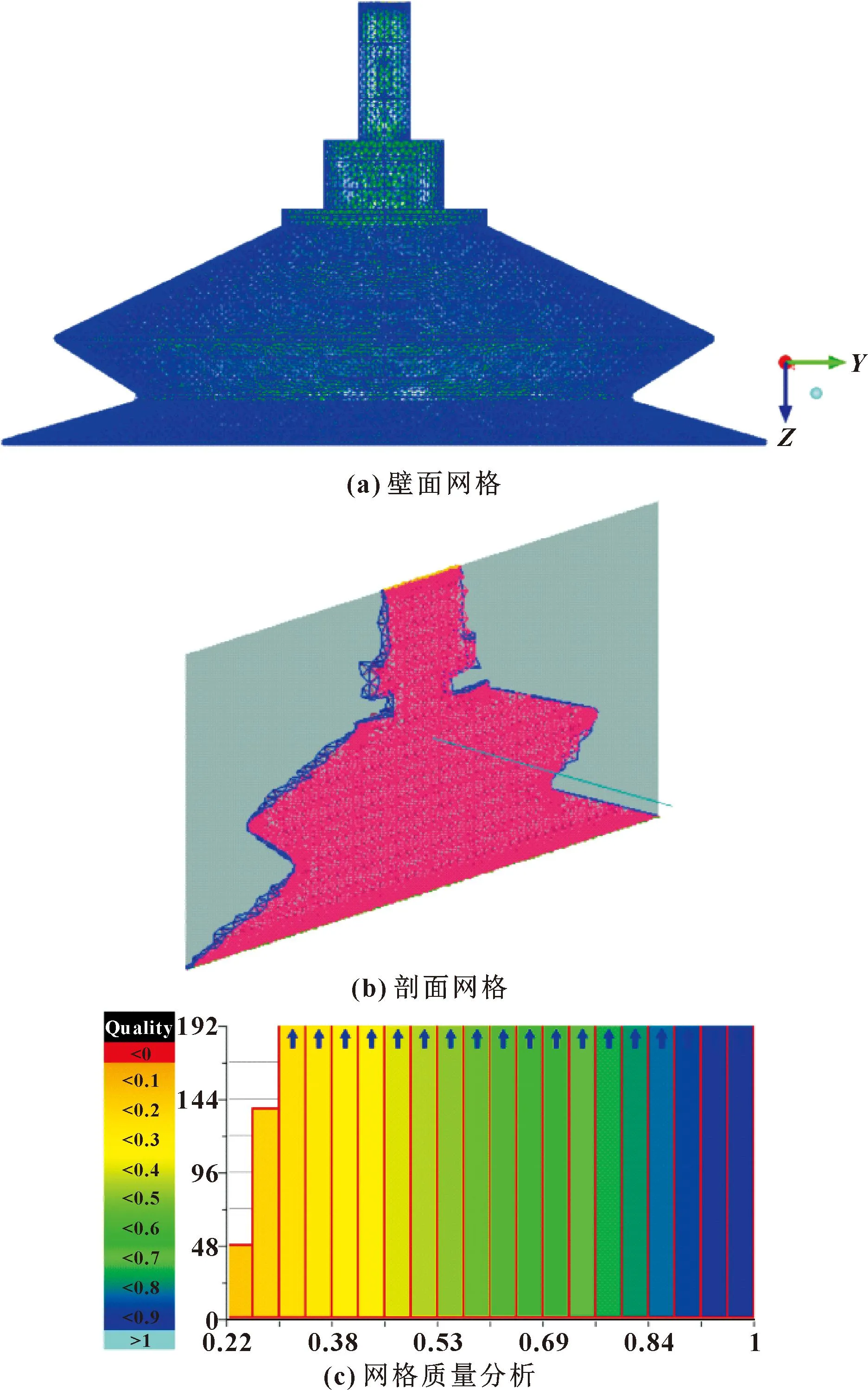
图5 流体计算域网格模型Fig.5 Mesh model of fluid computing domain：(a)wall mesh；(b)section mesh；(c)mesh quality analysis

为提高吸盘流场建模和数值模拟精度，对流场入口区、出口区及局部微小结构进行网格加密处理，同时通过网格质量分析和光顺处理，消除负体积单元和冗余节点，直至网格数量和质量达到精度要求。划分网格过程中，为更好地适应流场边界条件及其运算，在壁面附近设定边界层[14]，其中，第一层网格高度为0.05 mm，增进比为1.3，划分层数为22。

4.3 迭代残差

利用FLUENT对吸盘内腔流域进行数值模拟，构建基于标准k-ε两方程模式的单相稳态湍流模型，假设流场状态为完全湍流，则其雷诺数Re>10 000。由于进出吸盘的流体介质为空气，所以定义外部操作环境和入口区大气压力为1个标准大气压(101 325 Pa)[15]，同时参考实际真空度计算结果，将出口区压力设定为-55 kPa。

根据图4所示力学模型设定流场边界条件，沿Y轴正向定义重力加速度。对吸盘流体计算域进行初始化处理，采用Simple算法、标准壁面函数和二阶迎风格式对流场进行压力-速度耦合求解，并对连续性残差(c)、湍动能(k)及湍流耗散率(ε)迭代计算过程进行实时监测，如图6所示。可以看到，经过235步迭代计算后，3条残差曲线均趋于平稳，说明数值模拟结果满足收敛性要求。

图6 残差变量曲线Fig.6 Residual variable curve

5 流场分析与讨论

5.1 压力分布

5.1.1 纵截面压力场

在真空负压形成过程中，吸盘内腔将会受到静压和动压变化的综合影响[16]。由于吸盘为360°轴对称结构，故提取其纵截面流域进行压力场分析。

由图7(a)所示静压云图可知，出口管道流域存在较大负压分布，尤其是在管道底部过渡流域，局部负压明显偏高，最大压力高达约-106 100 Pa；相比之下，吸盘内腔其他流域静压场均为正压，最大静压约102 616 Pa，主要分布于吸盘底面与出口管道下部之间，且静压力分布相对均匀，说明在气流静止或流动稳定状态下，该流域承受的静压大小基本一致。

从图7(b)所示动压分布来看，出口管道以下内腔流域的动压状态十分稳定，且基本都接近于0，表明在流场动压作用下，使这一流域形成了较大真空区；与之形成鲜明对比的是，出口管道中线区域附近的动压高达154 017 Pa，压力值远远大于内腔真空流域，由此产生的压力差有助于气流流动和负压形成，对于缩短抽气响应时间和快速达到稳定吸附具有积极作用。

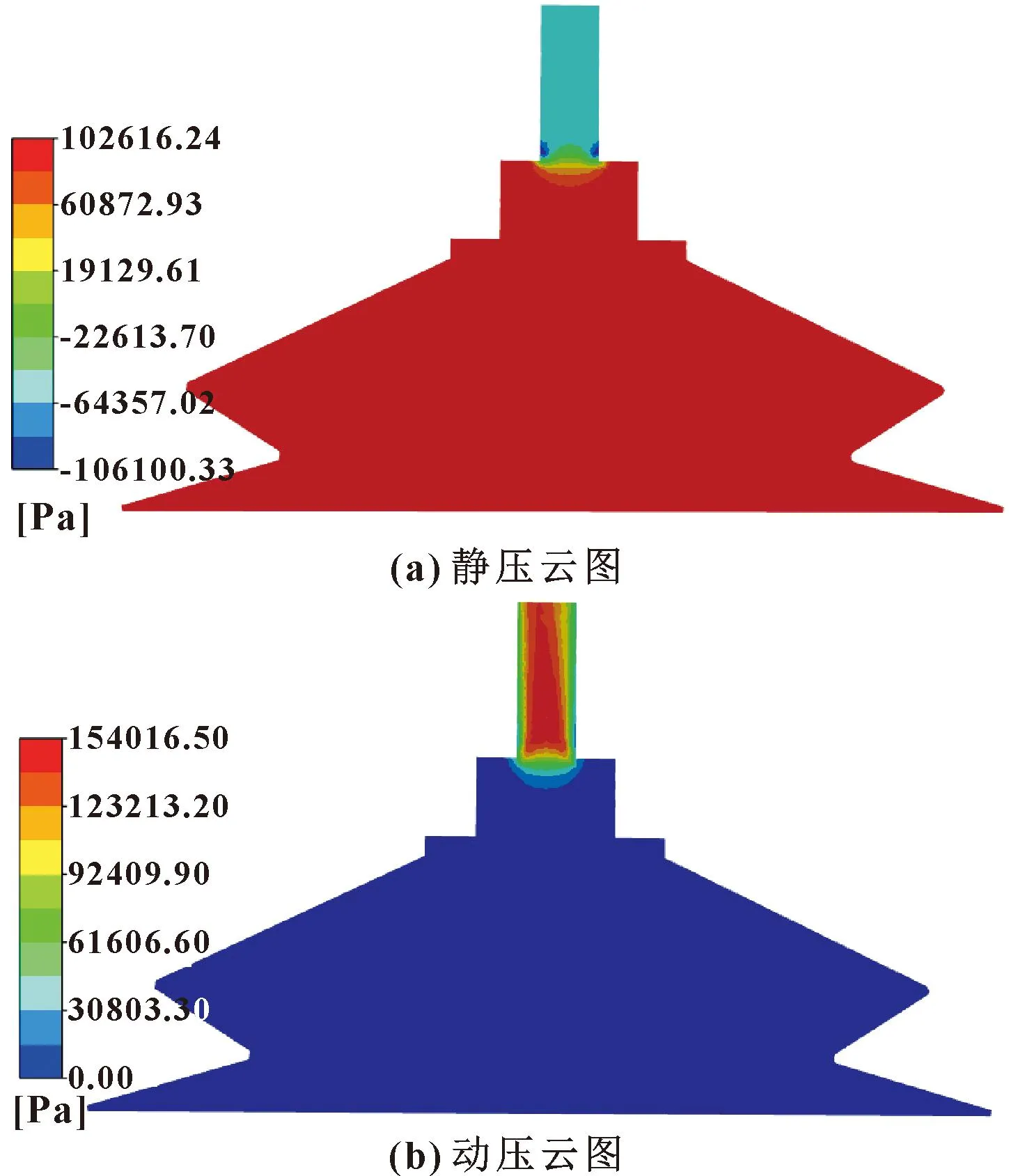
图7 纵截面压力场Fig.7 Pressure field of vertical section：(a)static pressure nephogram；(b)dynamic pressure nephogram

5.1.2 进、出口压力场

图8示出了进、出口区压力云图。对比进、出口区静压云图发现，进口区的边缘区域和中心区域压力分布较为均匀，且压力值明显较大(约101 328 Pa)，如图8(a)所示；而两者之间所夹环形区域高低压变化十分突出，说明这一流域静压稳定性较差。相比之下，出口区静压只在外环边缘存在微小的局部高压区，最大压力约-54 106 Pa，如图8(b)所示；而其他流域动压场分布则相对平稳，压力区间为-55 087～54 760 Pa，这与真空发生器真空度十分接近(-55 000 Pa)。由此可知，吸盘流体计算域具有良好的边界条件和模拟精度，符合真空发生器工作预期。

动压在进口中心区域存在一定压力波动，最大压力约6 163 Pa，如图8(c)所示；其他流域的动压变化没有明显起伏，且压力相对较小，最小压力约0.05 Pa。出口区的动压云图呈明显梯度分布，压力值从出口中心附近由内向外逐层减小，如图8(d)所示，最大动压区位于出口中心附近区域，此处压力值约140 736 Pa，远大于进口区动压。由此可知，在抽真空吸附过程中，动压分布会使气流不断从低压入口区流向高压出口区，直至吸盘内腔形成饱和负压并产生稳定吸附力。

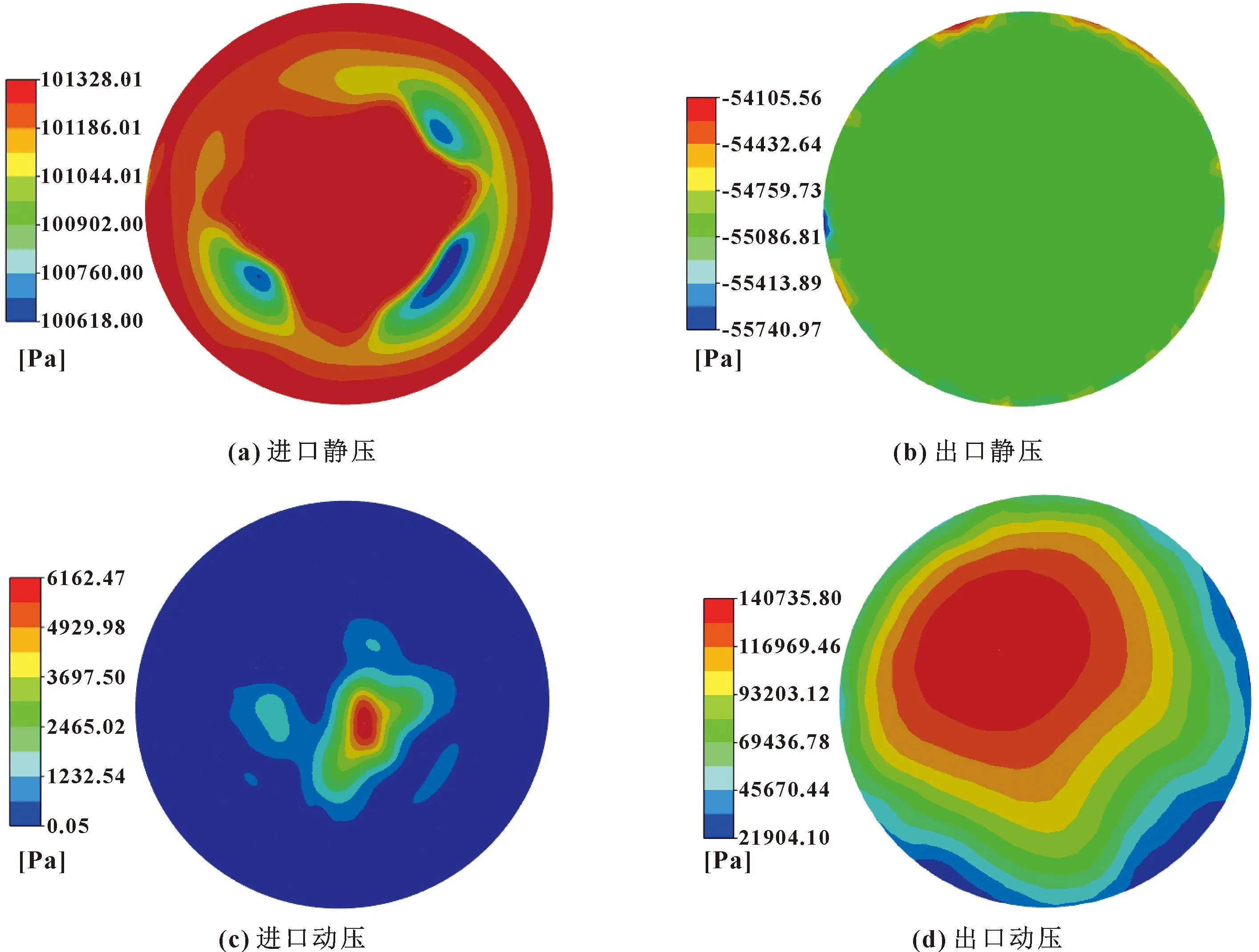
图8 进、出口区压力云图Fig.8 Pressure nephogram of inlet and outlet：(a)inlet static pressure；(b)outlet static pressure； (c)inlet dynamic pressure；(d)outlet dynamic pressure

5.2 流速状态

5.2.1 速度矢量场

在流场负压形成过程中，由于壁面边界层影响，使其附近流域黏度明显增大，所以分布于壁面之上的气流速度很小。图9所示为壁面三维速度矢量场，可知出口管道壁面大部分气流流速在190～286 m/s之间，而其以下壁面流速基本都接近于0。据此可知，吸盘流场边界层上的气流活跃区主要位于出口管道壁面。

图9 壁面三维速度矢量场Fig.9 Three dimensional velocity vector field on the wall

图10所示为二维速度矢量场。当真空发生器启动工作后，吸盘内腔平衡态瞬间被扰动，如图10(a)所示，由于抽真空作用，吸盘纵截面流域产生了多处旋涡型湍流速度，在此状态下，气流会按照矢量箭头方向从底部汇聚流向出口区，且气流流速从下至上在逐渐增大，尤其是在出口管道流域，气流速度高达近503 m/s，远远大于腔内其他流域气流速度。可见，吸盘内腔中心区域气流首先会被吸出，而壁面和其他流域气流则会被随后吸出，直至形成稳定的流场负压。

对比图10(b)、(c)所示进、出口面的气流速度矢量场，发现2个圆形区域的气流流速都是从中心区域向外围逐渐减小，且气流流速差值十分明显。其中，出口面中心区域气流流速高达480 m/s左右，约为入口面中心区域流速(约100 m/s)的4.8倍，说明负压流场具有较高的抽气响应速度，有利于吸盘快速达到稳定吸附状态。

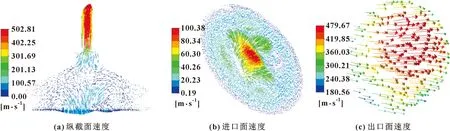
图10 二维速度矢量场Fig.10 Velocity vector field on the plane：(a)longitudinal section velocity；(b)inlet surface velocity；(c)outlet surface velocity

5.2.2 流速曲线

为进一步明确流场速度分布状态，在吸盘内腔关键流域定义3条几何截线，如图11所示，分别为截线A-B、截线C-D及截线E-F，用以表征吸盘中轴线区域、出口区域及入口区域的流速分布状态。

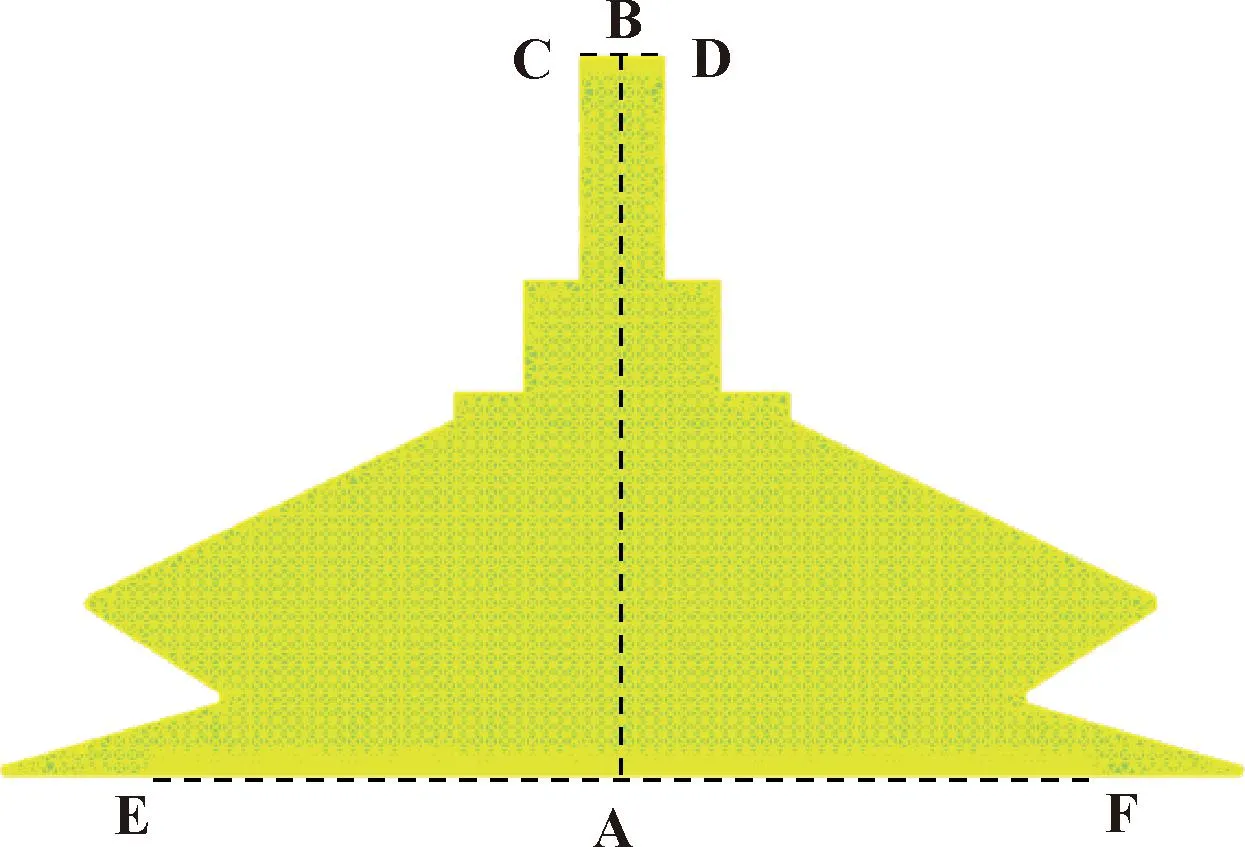
图11 几何截线定义Fig.11 Definition of geometric line

沿各条截线长度方向提取速度分布曲线，如图12所示。分析A-B段速度曲线可知，从点A至点B，气流速度分布呈总体爬升状态，如图12(a)所示，符合纵截面速度矢量场分析预期。

入口区中心截线E-F速度曲线类似状态分布，即截线中心区域气流速度大，而两端点区域附近气流速度明显偏小，如图12(b)所示；与之相比，出口区中心截线C-D速度曲线变化则较为平缓，如图12(c)所示，从曲线变化趋势可知，气流速度从出口区中心沿径向逐渐向两侧边缘区域减小。

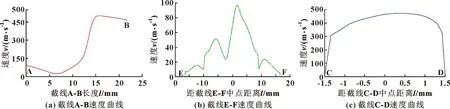
图12 关键流域速度曲线

显然，对比图10(b)、(c)所示进、出口面的速度矢量场可知，沿截线E-F和截线C-D的速度曲线与其矢量场分布特征完全匹配，通过提取速度曲线上各点的横、纵坐标，即可获得相应流场位置的流速状态，进而为负压流场速度变化规律分析提供有力依据。

5.3 流线轨迹

通过流线轨迹能够准确表征吸盘内腔气流流动方向及路线。图13示出了气流流线轨迹。在负压形成过程中，吸盘底部气流沿着弯曲轨迹逐渐流向上部管道出口，如图13(a)所示，大部分气流轨迹和流向较为规律。然而，在流场底部左右区域各存在两处形态相似的涡旋气流，而且涡旋分布位置基本对称。由此可见，吸盘负压流场存在典型的湍流特征，这一现象在壁面流线轨迹分布上体现得更为突出，如图13(b)所示，壁面流域的流线方向和轨迹分布十分杂乱，整体流线分布状态呈现出明显湍流特征，符合标准k-ε两方程物理模型对于流场模拟的理论预期。

图13 气流流线轨迹Fig.13 Airflow trajectory：(a)longitudinal streamline； (b)wall streamline

6 吸盘静力学分析

6.1 有限元模型

吸盘在负压作用下会产生应力和变形，其结构力学性能对于稳定吸附具有重要影响[17]。在WorkBench环境下构建吸盘有限元模型，由于吸盘具有典型轴对称特征，因此只取其1/4结构进行有限元分析，如图14所示。

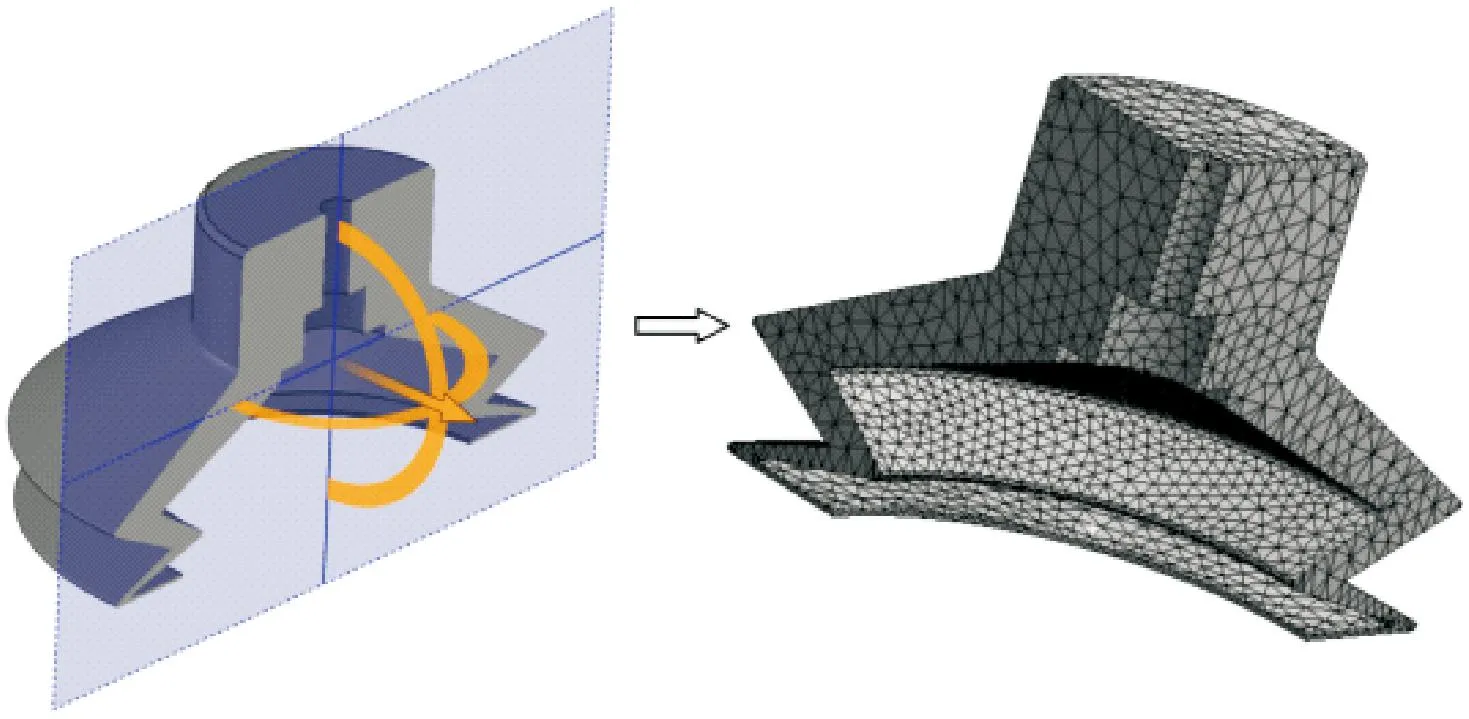
图14 吸盘有限元建模Fig.14 Finite element modeling of suction cup

采用四面体单元对盘体结构进行网格划分，离散结果共产生21 675个单元和38 713个节点。吸盘由硅胶材质制成，其质量密度为1 120 kg/m3，弹性模量为1.2 GPa，泊松比为0.48。

6.2 壁面总压

仿生壁虎在吸附机动过程中，吸盘在真空负压作用下产生吸附力，此时，吸盘内壁主要承受腔内负压作用[18]，所以有必要通过内壁总压对盘体进行有限元静力学分析。根据流体动力学理论，流场静压与动压之和称之为总压，如式(8)所示。

(8)

式中：pt为总压；pj为静压；ρ为流体密度；v为流体速度。

在CFD-POST模块中读入FLUENT流场分析结果，并通过探测操作获取吸盘内壁承受的总压力。考虑到吸盘结构对称性，可认为流场壁面总压为均匀分布[19]，因此，只需获取某一探点压力值即可近似表征该区域壁面压力，如图15所示，在真空度达到最大时，可将流场壁面划分为2个主要压力区，分别为盘体主壁面和出口管道壁面，即探测点1(101 397 Pa)和探测点2(-55 473.9 Pa)。

图15 壁面总压探测Fig.15 Probe of total pressure on the wall

6.3 应力与变形

根据吸盘垂直吸附状态设定约束边界条件，并将探测点1和探测点2的总压施加于壁面之上，在此基础上进行有限元静力学分析，提取壁面应力和变形结果。结果如图16所示。

从图16(a)可知，出口管道壁面和上盘壁面的应力分布十分均匀，且压力值明显较小(约547 Pa)。与之相比，下盘面底部区域应力变化较为突出，尤其是在内壁边缘局部区域(A区)，存在明显的应力集中，最大应力达到181.3 MPa，如图16(b)所示，可见该处为吸盘薄弱区域，应适当加厚该区域壁厚设计，以提高吸盘静力强度和工作寿命。

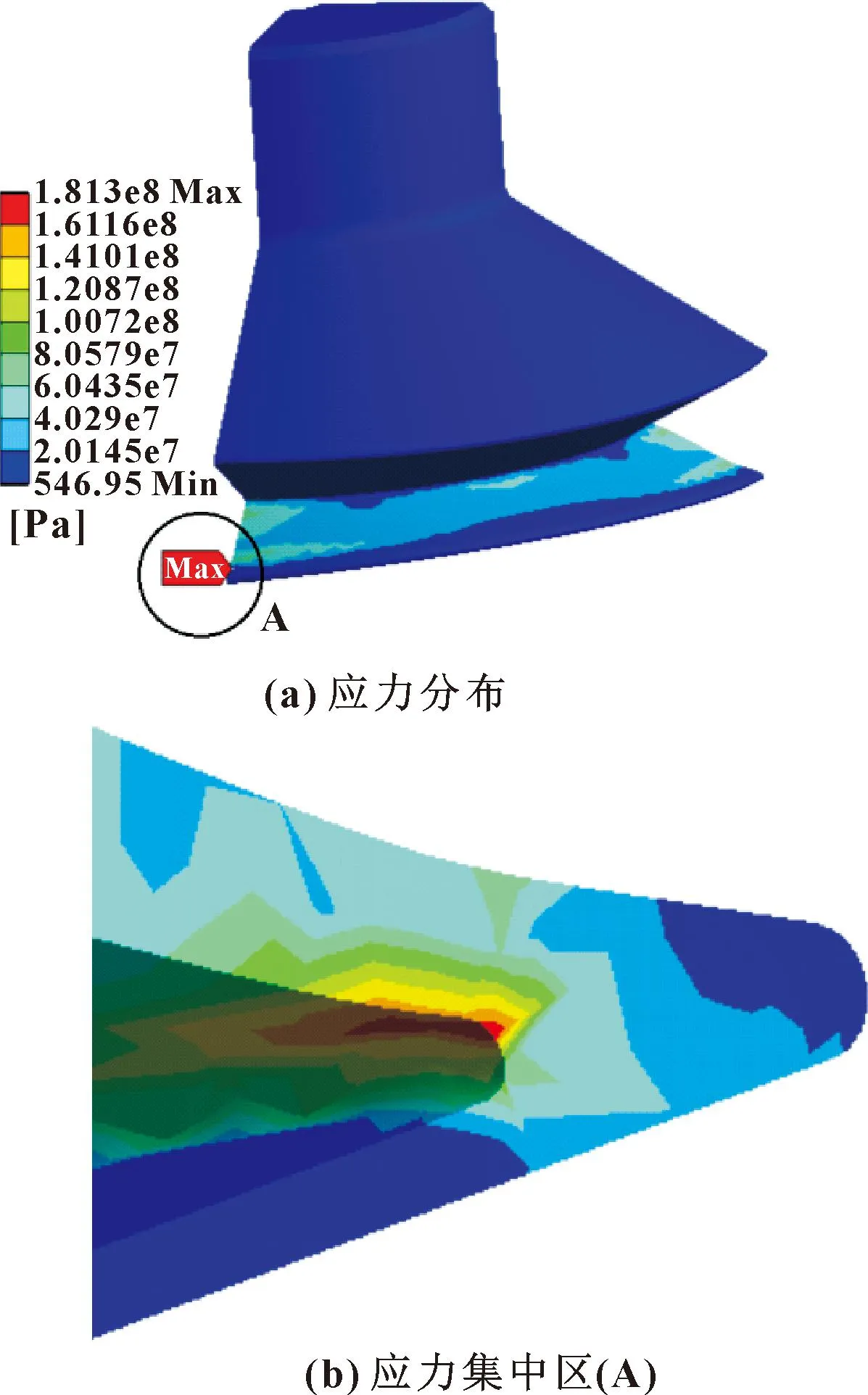
图16 应力分析结果Fig.16 Stress analysis results：(a)stress distribution； (b)stress concentration zone (A)

由于腔内真空负压作用，吸盘在吸附时会因发生变形而被紧压于壁面之上。图17所示为静力变形分析结果。可知，相对于原始未变形状态(图中线框)，吸盘在壁面总压影响下沿轴向和径向发生了不同程度的位移，且变形幅度从上而下逐渐减小，其中，最大形变区域发生于出气管道上部区域，最大变形量约0.07 mm。可见，变形量十分微小，加之硅胶吸盘具有较强弹性，所以静力变形不会对吸盘结构产生不利影响。

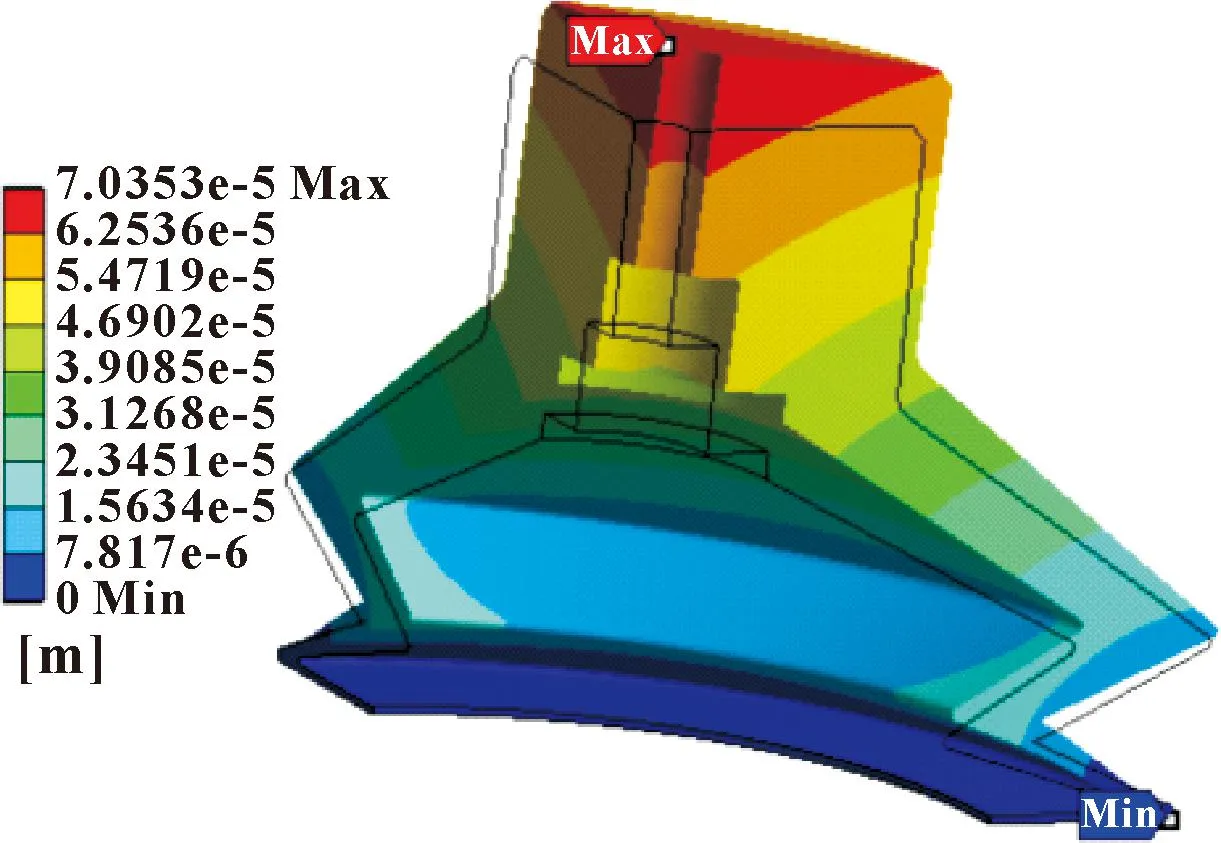
图17 静力变形分析结果Fig.17 Static deformation analysis results

7 样机与试验

7.1 数字化仿生造型

以壁虎原型为参考，通过体态特征分析和功能模块划分，在SolidWorks中对其仿生结构进行数字化设计与开发，如图18所示，利用特征建模方法设计各仿生关节三维实体造型，主要涉及头部、大腿关节、小腿关节、吸盘、躯干及尾巴等，仿生造型在满足功能要求条件下应尽量轻巧和美观。为提高仿生数字模型精度，装配设计过程需严格控制各构件之间的约束关系，避免出现干涉、碰撞或过定义等不利因素。

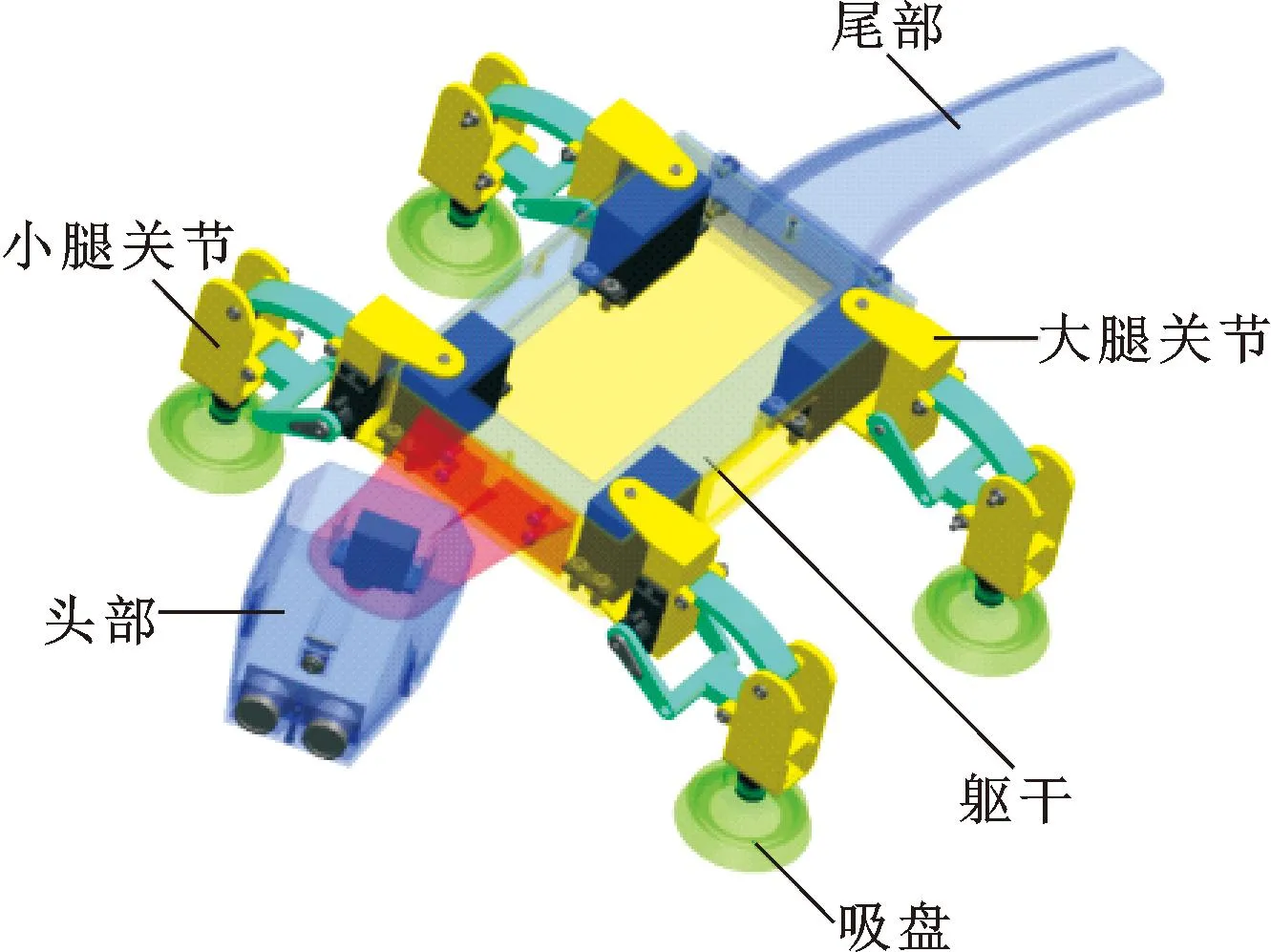
图18 数字化仿生造型Fig.18 Bionic modeling of digital gecko

7.2 吸附试验

通过数据处理对各构件实体造型进行格式转换，利用3D打印工艺制作其三维实体样件。针对仿生壁虎运动步态和电磁阀开关时序，开发基于Arduino的软硬件系统及控制程序，对此不予赘述。按照仿生机体方位布局将吸附气路分为左前、右前、左后及右后，如图19所示，在开展吸附试验时，先让左前、右前、左后及右后处的4个吸盘与垂直壁面接触，然后在电磁阀1和电磁阀2控制下开启真空泵，并通过三通、软管等将吸盘内部空气抽走形成真空负压，此时，4个吸盘在外部大气压力作用下被挤压吸附于壁面之上。

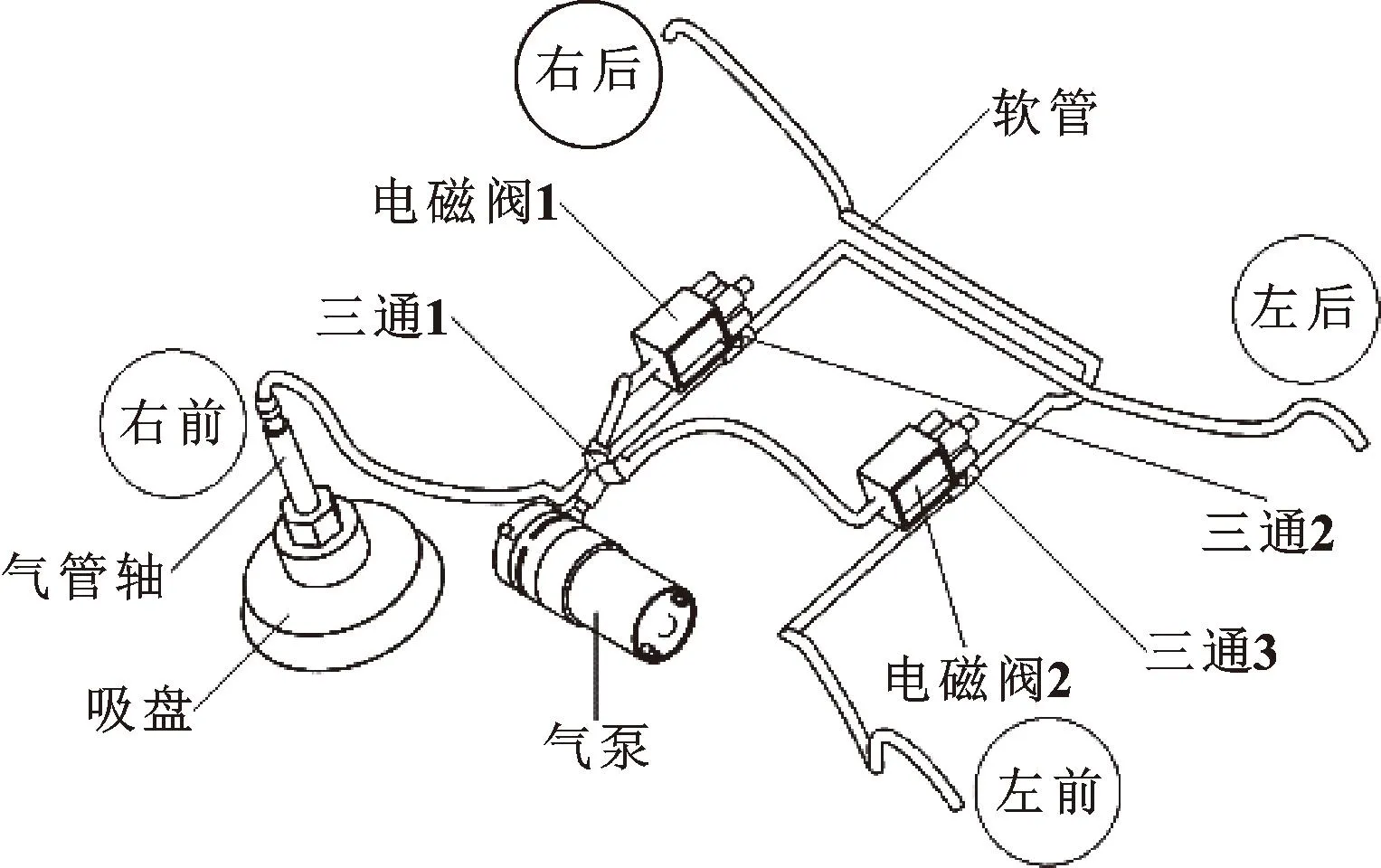
图19 吸附试验气路简Fig.19 Schematic of adsorption test

换步运动时，通过电磁阀关闭一处对角线位置的气动回路(如左前与右后，或右前与左后)，此时，由于关闭的对角线气动回路接通大气压力，所以吸盘因内外压力大小相等而恢复原形，并在驱动程序作用下完成吸附脱离与换步移动。需要注意的是，在吸附和移步试验过程中，应始终保持一处对角线吸盘处于吸附状态。

根据数字化仿生造型及其结构组成，装配和调试仿生机械壁虎试验样机，如图20所示，仿生机体由可充电锂电池供应电力，气动系统选用负压为-55 kPa的真空泵，腿关节通过舵机驱动来实现移步换位。

图20 吸附性能测试Fig.20 Adsorption performance test：(a)sucker action test；(b)adsorption climbing scenario 1；(c)adsorption climbing scenario 2

吸附测试结果表明，仿生机体可稳定吸附于垂直墙壁之上，在爬墙运动过程中，吸盘气动控制时序准确，且吸附与脱附动作切换灵敏、负压响应快，能够平稳实现仿生关节的移步换位与攀爬，具有良好的机动性与可靠性。

7.3 展望

由于负压吸附方式对于基底表面质量有着特殊要求，目前该仿生机体的吸附攀爬只适用于光滑壁面或微粗糙壁面，而对于粗糙度较大或环境更为恶劣的基底，则会产生不同的吸附效果，这也是吸附试验误差的主要来源。对此，还需在后续研究中不断进行探索与尝试，以期通过改进吸附方式或微观黏附阵列结构等来提升仿生壁虎的吸附可靠性。

8 结论

(1)通过标准k-ε两方程湍流模型构建单相稳态流体计算域，能够较为准确地表征和描述真空吸盘的负压吸附机制及其流场状态，为仿生机械壁虎的吸附模拟与技术研究提供了重要借鉴。

(2)在负压吸附过程中，吸盘出口管道区的动压和气流流速远大于内腔流域，尤其是出口面中心区域气流流速(约480 m/s)，约为入口面中心区域流速(约100 m/s)的4.8倍，对于快速响应抽真空和形成稳定负压具有积极作用。

(3)在壁面总压作用下，吸盘静力变形自上而下逐渐减小，且在盘体底面边缘区域存在明显的应力集中(约181.3 MPa)，应尽量增大该薄弱区域的壁厚设计，以提高吸盘的强度储备和使用寿命。

(4)通过仿生样机研制和吸附试验测试，验证了负压吸附思路及其实现方法的可行性。试验结果表明：该仿生机体具有良好的仿生动力学性能和负压吸附特性。研究结果为壁虎黏附阵列的仿生设计提供了借鉴，具有可期的技术发掘潜力和实践应用价值。