基于流体域仿真的高速风机气浮箔片轴承动静特性研究

张晨，许亮，孙丹，李雨薇，高飞，荆建平

(1.上海交通大学机械系统与振动国家重点实验室，上海 200240；2.中国船舶集团有限公司第七〇三研究所， 黑龙江哈尔滨 150078；3.新乡航空工业(集团)有限公司，河南新乡 453000)

高速风机作为航空、舰船、化工等工业领域常见的流体机械，其制造产业的提升对工业流体机械的发展尤为重要。对于风机而言，随着工作时间的增加，其动平衡会被逐渐破坏，轴承部位的振动会不断加大。一旦轴承的振动大于某一限值，就会对风机造成巨大的影响，必须停机修理[1]。随着科学技术水平的不断提升，风机应用的环境多变复杂，风机向着体积小、质量轻的方向不断发展，这对风机转子系统所使用的轴承的精度提出了更高的要求。气浮轴承凭借着精度高、发热小、噪声低等各项优点，正在逐步替代传统的机械轴承，成为风机等高精度设备中的关键部件[2]。如今，气浮轴承应用于风机的转子系统中，针对风机类产品转子系统特性的分析、临界转速的预测等研究便是所需要解决的问题。目前市面上常见的商业计算软件均缺失较为系统的气浮轴承特性计算方法，气浮轴承的研究也在不断地发展与完善。

工业中的高速风机多数选择使用高速气浮轴承，结构如图1所示，该类轴承的特性计算难度更大[3]。并且，为了提高气浮轴承的抗冲击能力与自适应能力，在轴与轴承之间加入了具有柔性的金属箔片(见图2)，其能够根据转速与载荷的变化建立起合适的工作气膜厚度，同时箔片轴承的结构阻尼效应能够更好地抑制转子的振动，从而有更好的稳定性。因此对多叶箔片轴承的特性进行理论分析有更加重要的现实意义[4]。

图2 气浮轴承箔片Fig.2 Foil for air bearing

WALOWIT等[5-6]是较早研究波箔型箔片轴承的学者，他们将起支撑作用的箔片从轴承中分离，分析单个箔片的受力情况，建立对应的轴承模型，求解得到箔片轴承的静态特性。以HESHMAT为代表的一批学者对波箔型箔片轴承进行了比较深入的理论和实验研究，采用有限差分法来计算弹性流体动力润滑(EHD)问题，形成研究波箔型箔片轴承刚度和阻尼特性的经典理论方法[7-9]。

在国内，龚焕孙[10]最早开展波箔型箔片轴承刚度和阻尼特性的研究，他基于Krichhoff假设，施加载荷与边界条件进行计算，得到轴承静态特性，同时搭建实验台，对其静态特性进行试验研究，与理论分析的结果相符。宋来运[11]从理论和实验验证2个层面对动静压气浮轴承转子系统的静态性能、动态性能和动态稳定性等综合性能进行了系统性的研究，为设计研发高速高精度动静压气浮主轴系统提供理论基础和技术支持。刘佳琦等[12]从弹性箔片轴承的结构特性、涂层特性和建模方法3个方面对气体弹性箔片轴承的研究进展进行综述，展望弹性箔片轴承在高精尖等领域的前景，并对弹性箔片轴承的研究方向提出了建议。刘恒等人[13]对箔片含有预变形的多叶箔片气体动压轴承进行研究，将箔片简化为弯曲梁，推导出多叶箔片的变形方程和考虑预变形后的气膜厚度方程，计算研究转速等参数对轴承承载力的影响。

然而，当前的气浮轴承的特性计算多是基于一定的假设条件，通过简化轴承特性方程来得到轴承特性。郭军刚等[14]建立多叶油润滑箔片轴承Reynolds方程、对应的边界条件以及收敛条件，通过传递矩阵计算箔片轴承轴系临界转速，同时，建立对应的试验系统进行评估与验证。

由于众多假设条件的存在，计算结果往往与实际结果存在偏差。因此，为了提高高速风机转子动力学分析精度，减少理论计算与实际情况之间的偏差，本文作者针对现有的一类多箔片气浮轴承，建立流体域模型，通过使用商业仿真软件分析风机产品内高速气浮箔片轴承的静态特性与动态特性随着转速提升的变化规律，从而更加精准地预估风机模态、临界转速以及失稳转速。在设计使用气浮轴承的转子系统时，依据气浮轴承自身的动态特性变化趋势来设计对应的转子系统结构，从而能够更大程度地提高转子系统的稳定性与安全性，这是开展轴承作为支承部件的转子系统动力学特性研究的基础。

1 计算方法与流体域模型

针对使用气浮轴承的风机转子系统，气浮轴承中的多叶箔片在转子系统启动时，起到支撑作用；随着轴颈转速的不断提升，带动气浮轴承的流体域内的流体高速流动，由收敛楔进入发散楔，产生气膜；气膜可视作具有较大刚度的支撑体，具有足够的承载能力，随着气膜的动压力不断提升，将轴颈慢慢托起，与箔片中间形成空隙，不产生接触。当轴颈的载荷与气膜所能够提供的承载能力实现相互平衡时，即为气浮轴承的工作状态。

文中提出的轴承特性求解的方法原理如图3所示，主要过程为：首先建立气浮轴承的流体域模型，针对流体域模型进行网格划分，通过商用仿真软件模拟一定转速下气浮轴承流体域的分布情况；移动轴颈使得轴颈受到流体域的作用力与所受到的载荷相互平衡，从而得到气浮轴承在一定载荷下的轴心轨迹图，即为气浮轴承的静特性计算；在静特性的计算结果的基础上，赋予轴颈与气浮轴承转速相同的同频扰动，读取在扰动的作用下流体域对轴颈的作用力，并沿轴颈表面进行积分，得到轴颈沿X、Y轴方向的受力变化，从而计算气浮轴承的刚度与阻尼系数，即为气浮轴承的动特性计算。

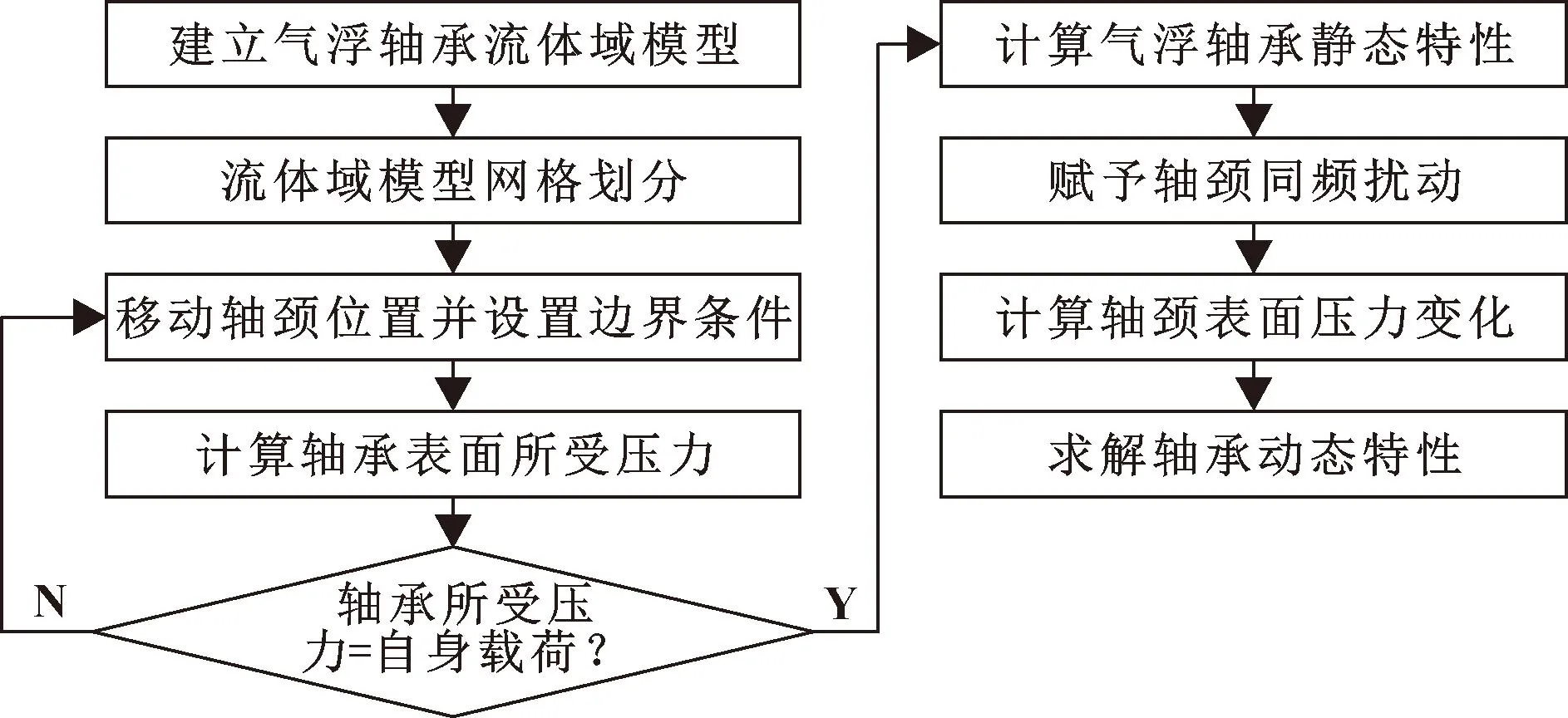
图3 轴承特性求解流程Fig.3 Flow for solving bearing characteristics

建立气浮轴承的流体域模型时，为了更加便于仿真计算与后续的模型修正，基于流体域沿轴向分布变化较小的情况，建立流体域二维平面模型。使用该模型进行模拟仿真，得到流体域结果后，通过使用修正系数，将二维模型计算结果进行修正，得到三维流体域模型的结果。

文中研究的气浮轴承流体域内的流体为可压缩气体，使用商业仿真软件根据气体的连续方程与动量方程等进行求解，通过仿真模拟计算得到气浮轴承流体域内的气体分布情况以及轴颈表面的压力分布，列出轴颈的受力方程，从而可以求解得到8个动特性系数[11]。

在转子轴心附近产生一个小扰动Δx、Δy，流体域对转子的作用力ΔFx、ΔFy为

(1)

将位移与受力取谐波分量可得：

(2)

(3)

将谐波分量代入式(1)，可得：

(4)

求解该方程组，即可得到气浮轴承的刚度系数与阻尼系数。

2 模型网格划分与边界条件设定

2.1 模型网格划分

由于气浮轴承结构特殊性，为满足CFD仿真模拟计算得到的流体域结果的精确度同时提高计算过程效率，选择使用流体域二维模型进行仿真计算[11]，同时需要对流体域进行高质量的网格划分，得到更合适的网格结构。网格分为结构化网格与非结构化网格，因为该类气浮轴承的流体域模型比较简单，且比较规则，没有太多复杂的流体区域，因此，选择划分结构化网格。该类网格生成速度比较快，并且数据结构简单，可以满足气浮轴承流体域的仿真计算。网格单元越小的情况下，得到的计算结果精度更高，但同时会增加仿真模拟的计算时间；且在仿真模拟计算的过程中，需要控制轴颈移动，导致流体域随之改变，涉及动网格设置问题，对网格的质量要求也随之提高。因此，需要选取满足计算精度的网格尺寸与网格数量。文中采用的结构化网格划分流体域模型(见图4)，经过网格无关性验证，采用网格数量分别为51 090、239 820、420 000与802 670的流体域模型。在该网格数下分别移动轴颈至工作转速下的位置，得到的误差如图5所示。可以看出，节点数为399 800，网格数量为420 000的网格划分得到的模型即可满足仿真计算求解的精度要求。质量较高的流体域模型网格为后续的气浮轴承静特性与动特性的计算求解奠定了基础。

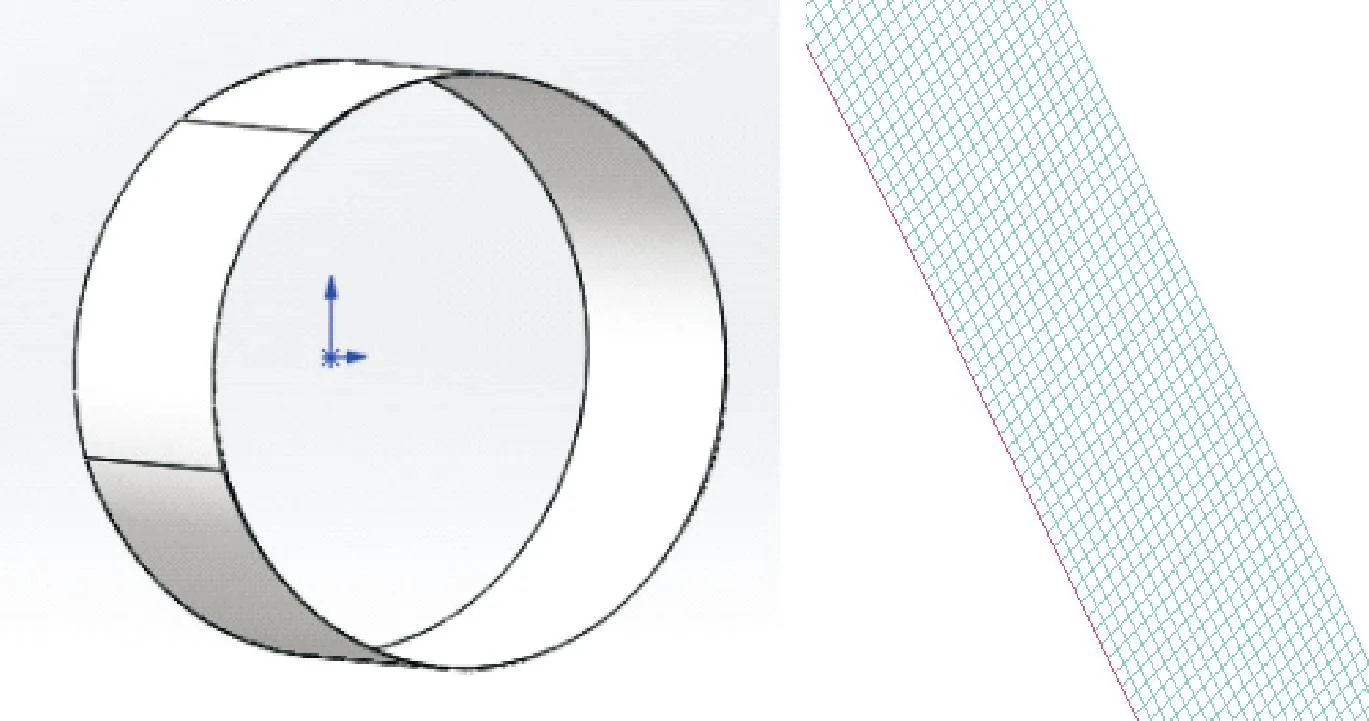
图4 气浮轴承流体域模型及网格划分示意Fig.4 Fluid domain model and grid generation of air bearing

图5 网格无关性验证Fig.5 Grid independence verification

2.2 模型边界条件设定

使用该类气浮轴承的风机转子系统的工作转速为100 000 r/min，轴颈所受到的载荷为转子自身的重量3 N，流体域内的材料为可压缩气体，气体的密度为8.13 kg/m3，气体的压缩系数为1.4，在仿真模拟的计算过程中不考虑气体黏性的影响，气体的压力为800 kPa。模拟仿真的求解选择Pressure-Based，Velocity Formulation选择Absolute，Time选择Transient，2D Space选择Planar。

模型的设置中，Energy选择On，Viscous选择SSTk-ε，该模型可以较好地处理求解边界层网格数据，在近壁面的位置能够更好地进行处理。因为气浮轴承的流体域模型的特点，可以看出，k-ε模型能够更高精度地处理求解流体域内的流动情况；同时，选用SST，相较于BSL，依然保留了在近壁面采用k-ε模型，但SST简化了模型，减小计算量，对壁面的距离更加敏感，能够进行更加精确地仿真求解；同时，壁面的设置中加入轴颈的转速与流体域的压力边界条件，以及考虑移动轴颈的动网格，根据轴颈位置的改变来调整网格结构。最后，根据网格的尺寸与轴颈的移动设定合适的时间步长与时间步数来得到更加精确的结果。得到静特性的计算结果之后，赋予轴颈同频扰动，求解得到轴颈表面的压力分布，对轴颈表面进行积分得到轴颈沿X、Y轴方向受到的作用力，从而求解得到气浮轴承的刚度系数与阻尼系数。完成100 000 r/min工作转速下的气浮轴承的特性计算之后，继续求解60 000、80 000 r/min转速下的气浮轴承的特性，从而得到气浮轴承从开始启动到转速提升至工作转速这一过程中轴心位置的变化以及气浮轴承的静特性与动特性的变化趋势。

3 仿真结果及分析

对气浮轴承流体域模型进行计算流体力学求解并进行仿真计算，可以得到在不同的转速下，气浮轴承流体域内的气体速度分布、湍动能分布以及气体压力分布情况。图6、7、8所示为100 000 r/min转速下气浮轴承流体域内气体的速度、压力分布情况以及流体域内的湍动能分布。

从图6中可以看出，在流体域内靠近轴颈边界的气体速度较大，随之速度沿径向方向不断下降，在箔片边界附近的气体速度最低，与实际情况相比较为符合。从图7中可以看出，流体域内气体的压力最大值发生在流体域厚度最小附近，该现象产生的原因可由流体动压润滑理论解释。流体动压润滑是指轴颈在旋转时，在轴颈与轴承的摩擦表面之间会充满流体，由于流体自身具有黏性，当轴颈达到足够高的旋转速度时，流体会被轴颈带入轴颈与轴承表面之间的空间。对于文中所研究的气浮轴承，即为将流体带入轴颈与箔片之间的流体域内，在轴颈与箔片之间形成楔形间隙，从而形成流体动压效应；被带入楔形间隙的流体会产生压力，该压力与轴颈赋予的载荷(即为外载荷)平衡时，轴颈与箔片之间形成稳定的气膜，从而实现流体的动压润滑。因此，流体域内气体的压力分布情况与理论分析结果相符合。如图8所示，轴承的流体域内变化较大的湍动能主要发生在箔片搭接的位置，即为流体域内气体厚度较大的位置，因为该处为箔片搭接，流体域边界发生突变，边界的变化会导致流体域厚度随之改变，从而在此处更易发生湍流。

图6 100 000 r/min转速下流体域速度分布Fig.6 Velocity distribution in fluid domain at speed of 100 000 r/min

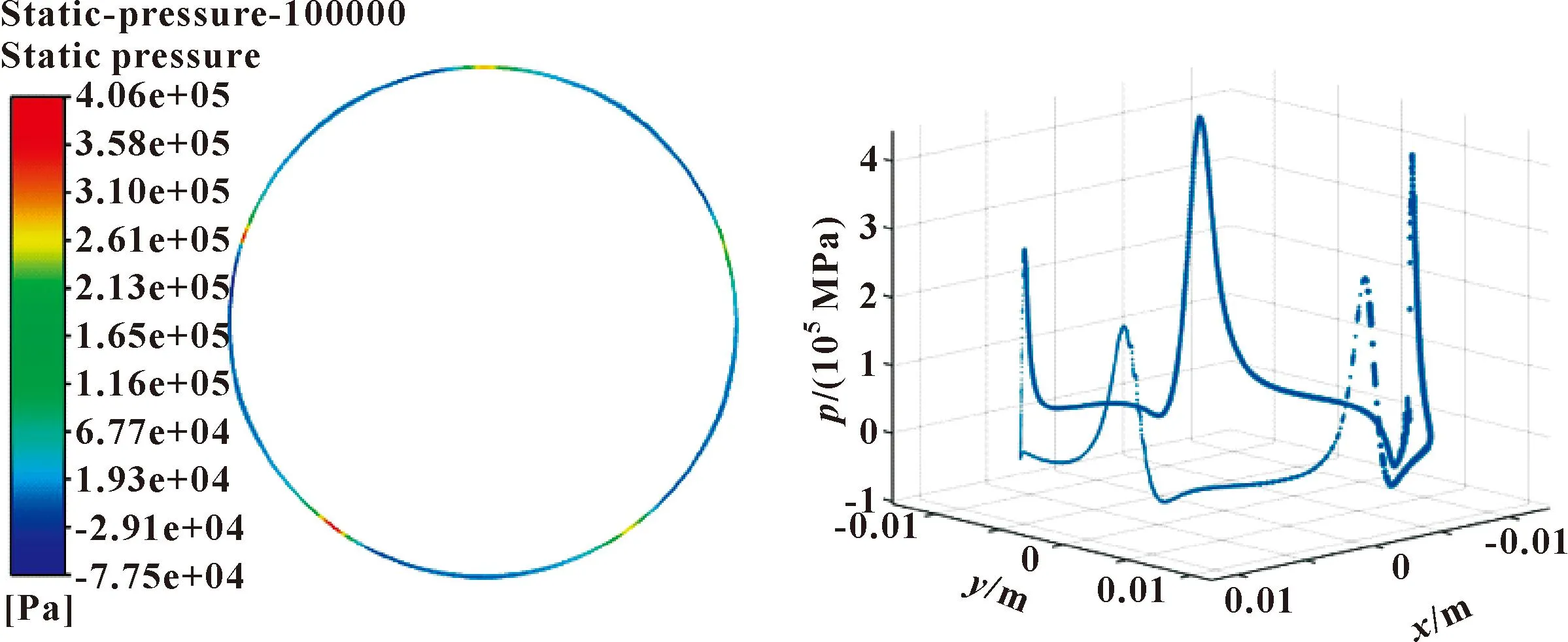
图7 100 000 r/min转速下流体域压力分布Fig.7 Fluid domain pressure distribution at speed of 100 000 r/min

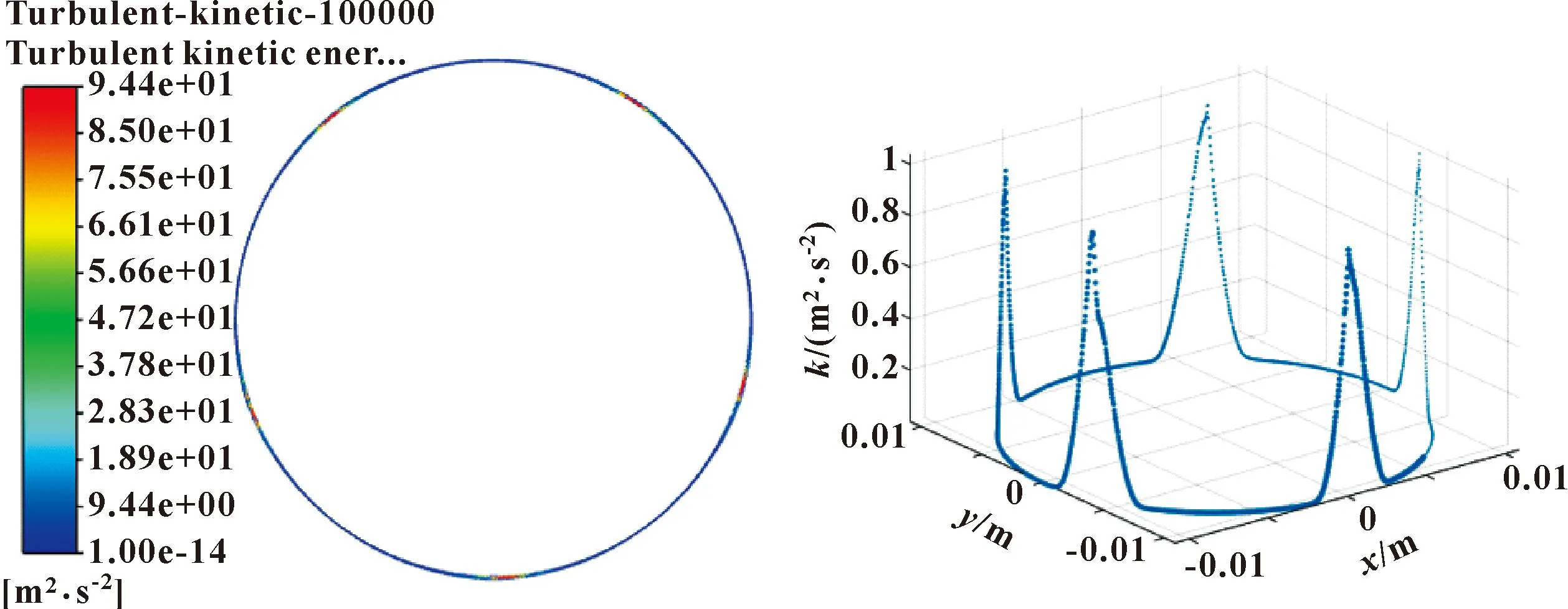
图8 100 000 r/min转速下流体域湍动能分布Fig.8 Turbulent kinetic energy distribution in fluid domain at speed of 100 000 r/min

图9—11所示为气浮轴承在80 000和60 000 r/min转速下流体域内的气体速度分布、湍流分布以及气体压力分布情况。

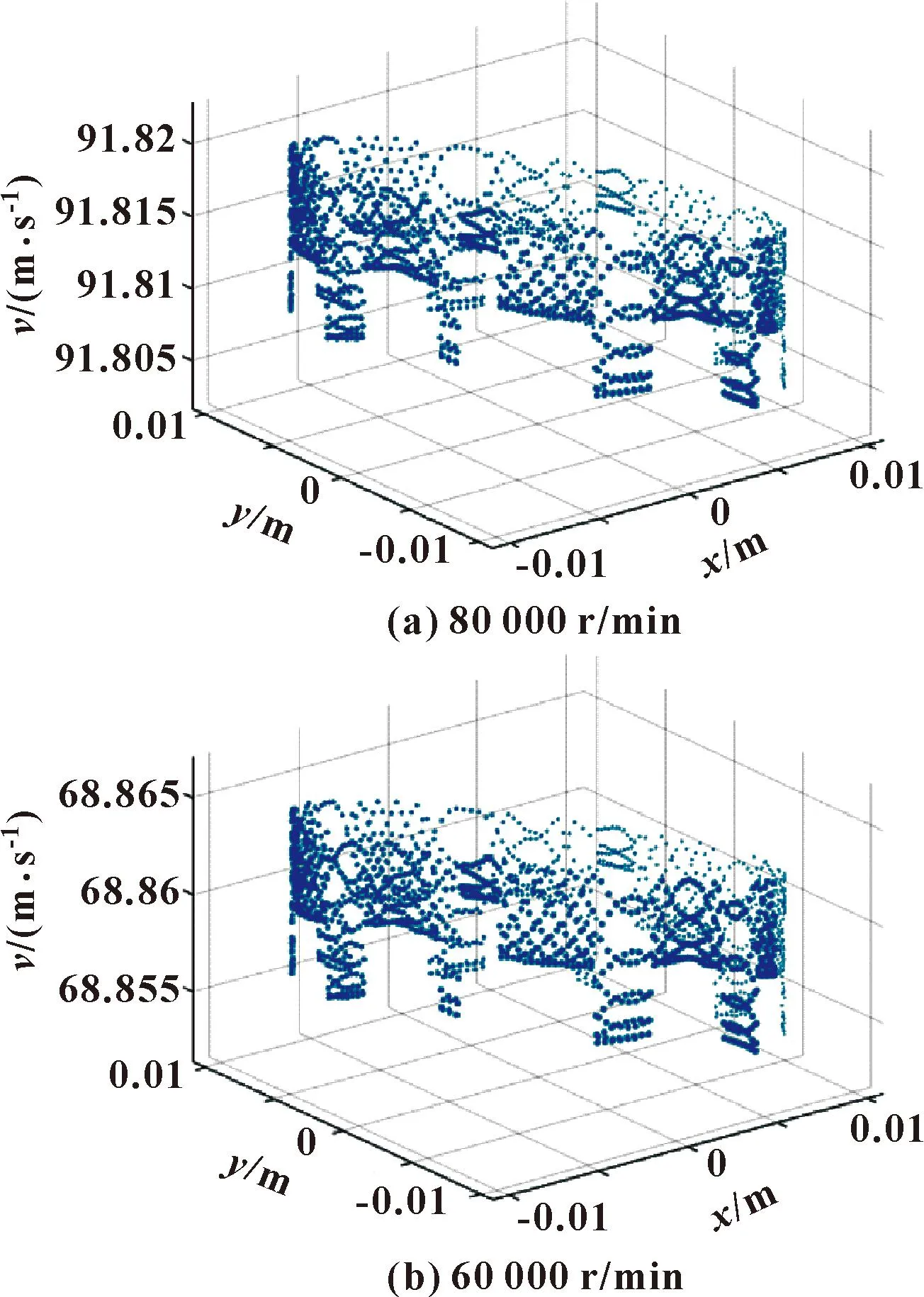
图9 不同转速下气体速度分布Fig.9 Speed distribution of gas at different speeds：(a) 80 000 r/min；(b)60 000 r/min

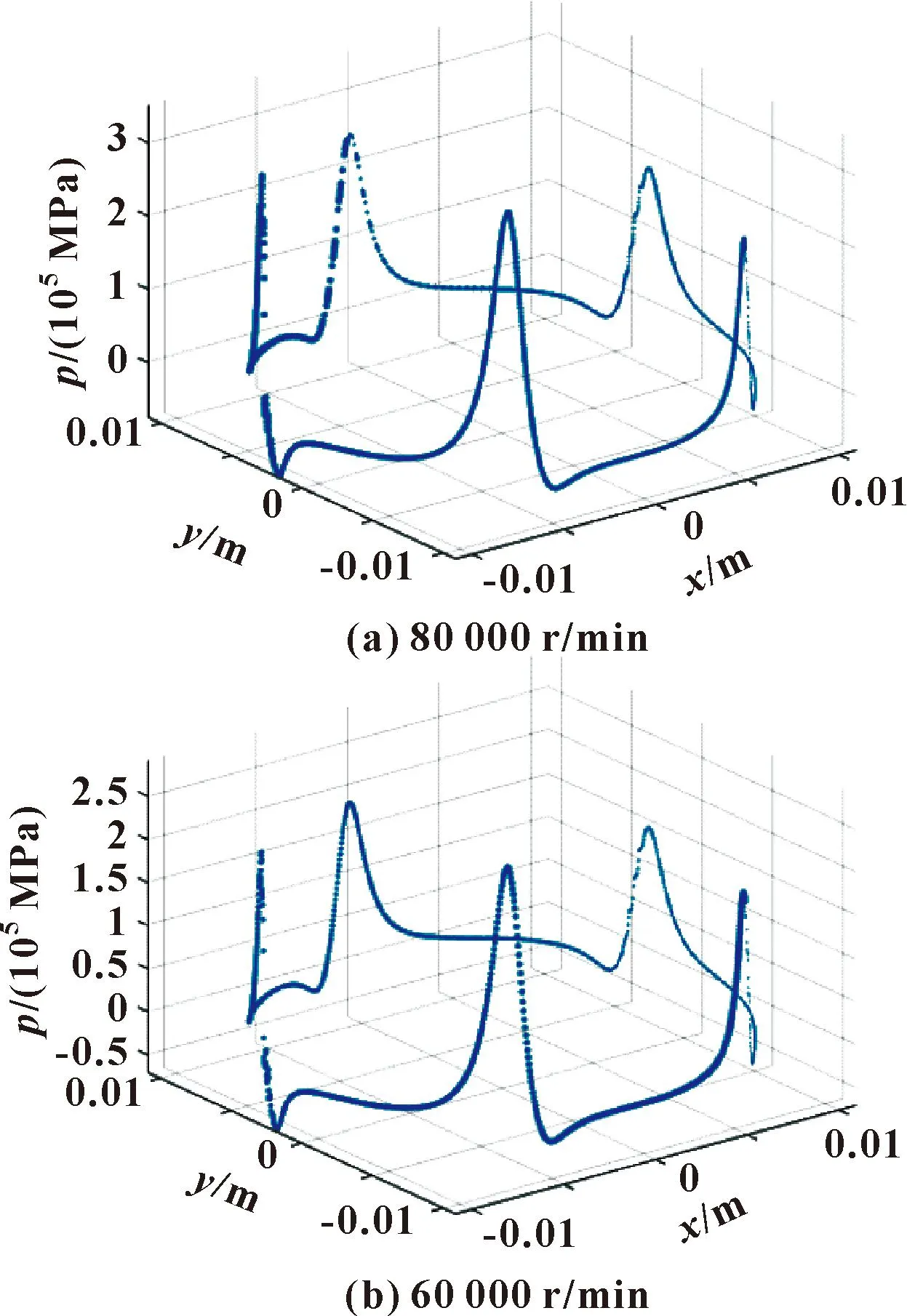
图10 不同转速下气体压力分布Fig.10 Pressure distribution of gas at different speeds： (a) 80 000 r/min；(b)60 000 r/min

图11 不同转速下气体湍动能分布Fig.11 Turbulent kinetic energy distribution at different speeds： (a) 80 000 r/min；(b)60 000 r/min

从图9—11中可以看出不同转速下，速度分布、压力分布以及湍动能分布情况以及变化趋势都大致相同，不同之处在于转速的变化，轴心位置会随之改变，承载相同压力的气膜形状发生变化，但气膜对轴颈的压力合力仍然保持与轴承的载荷相平衡，从而保证气膜能够稳定存在，轴颈能够正常运转。

根据赋予轴颈同频扰动后求解得到轴颈表面的压力分布情况，对轴颈表面进行积分得到轴颈沿X、Y轴方向受到的作用力，图12与图13所示为赋予轴颈同频扰动后，轴颈X、Y轴方向的位置变化与轴颈所受到的2个方向的压力变化情况。

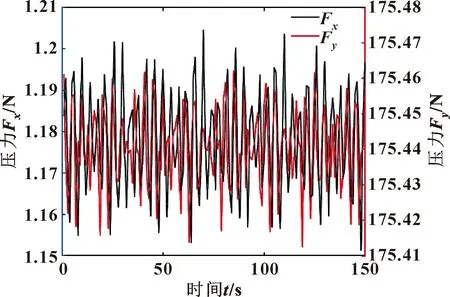
图13 轴颈表面压力变化Fig.13 Change of journal surface pressure

从图12、13中可以看出，轴颈表面所受到的压力随着轴心位置的变化呈现周期性变化的规律。因此，需要通过数据处理，从压力变化曲线中找到与轴心位置变化频率相同的曲线；同时求解轴心位置变化曲线与压力变化曲线之间的相位差，根据频率与相位差值即可得到求解刚度系数与阻尼系数所需要的压力变化表达式。使用相同的方法，赋予同一转速2个不同的同频扰动，处理数据得到对应的压力变化表达式，将表达式代入方程组内，从而求解得到气浮轴承的刚度系数与阻尼系数。图14与图15所示为刚度系数与阻尼系数随着转速提升的变化情况。

图15 阻尼系数随转速的变化Fig.15 Variation of damping coefficient with speed

从图14、15中可以看出，X轴与Y轴方向的直接刚度系数随着转速的提升不断下降，直接阻尼系数的变化趋势则是先下降而后上升；交叉刚度系数随着转速的提升先下降而后上升，X轴与Y轴的交叉阻尼系数的变化趋势则相反。这是因为根据动压润滑理论与方程可知，任意一点的气膜压力与该点的速度梯度的导数有关。因此，对于某一固定位置，当轴颈的转速较低时，轴颈偏心率较大；随着转速的提升，轴颈偏心率会逐渐减小，在此过程中，该点的速度梯度对应发生变化，从而产生的气膜压力也随之发生改变，代入方程求解得到的刚度系数与阻尼系数呈现不断下降的趋势。随着轴颈转速的不断提升，轴颈的偏心率变化会不断变小，该位置的速度梯度会随之增大，产生的气膜压力也不断提高，从而会使得刚度系数与阻尼系数随着转速的不断提升呈现前后不同的变化趋势。

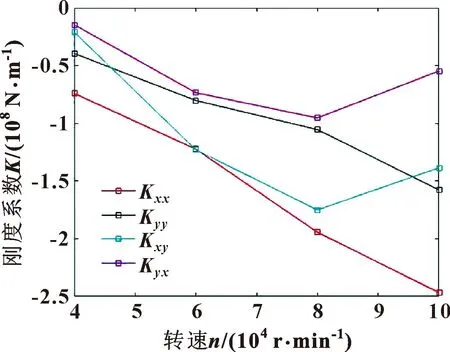
图14 刚度系数随转速的变化Fig.14 Variation of stiffness coefficient with speed

4 结论

建立了高速气浮轴承流体域模型，通过仿真计算方法求解了轴承特性，分析了气浮轴承工作状态下稳定时的轴心位置随着转速提升对应的变化情况，以及气浮轴承的动态特性系数与转速的关系，发现随着转速的不断提升，稳定时的轴心位置会逐渐向气浮箔片轴承的圆心靠近；同时，轴承的直接刚度系数在一定的工作转速范围内随着转速的提升而下降，直接阻尼系数则在工作转速范围内下降到达低值后上升。研究结果可为预估风机的失稳转速与临界转速提供理论支撑。