框架承担倾覆力矩的合理计算方法

常 磊, 崔济东, 廖 耘, 周 定, 李盛勇

(广州容柏生建筑工程设计事务所，广州 510170)

0 引言

现行《高层建筑混凝土结构技术规程》(JGJ 3—2010)[1](简称高规)基于结构底层框架部分承受的倾覆力矩占比大小来判别结构的抗侧力体系;而对于框支剪力墙结构,高规10.2.16条要求,框支框架承担的地震倾覆力矩应小于结构总地震倾覆力矩的50%。现行《建筑抗震设计规范》(GB 50011—2010)[2]6.1.3条与高规10.2.16条相似,给出了框支框架承担的地震倾覆力矩的上限,同时在其条文说明中给出了计算方法(简称抗规法),这是结构设计相关规范规程中出现的唯一算法。

基于抗规法,文献[3]提出了统一解法(分为柱剪法和梁剪法)。该方法从理论上推导而出,且文献[4]对其在工程实践中的意义进行了阐述,特别在结构抗震体系的判断和剪力墙端柱暗柱的可靠设计上有较大改进,同时也给出了结构中斜撑的抗倾覆贡献表达,并利用诸多典型案例进行了应用分析[5],虽表明该方法合理可行,但尚未对其进行系统总结,也未给出其力学法下的准确表达。

所谓力学法即视上部结构为隔离体从首层柱底反力来计算,结果当属于框架承担倾覆力矩的概念范畴。力学法有诸多计算表达方法[6-9],部分方法已被国内设计软件广泛采用。在PKPM、YJK等设计软件中的轴力法也即陈晓明[6]提出的力学法,简称“轴力法”,YJK软件中改进的轴力法[8]简称“改进轴力法”。此外,文献[9]提出的力偶法(简称称“力偶法”)将结构总倾覆力矩分为3大力偶,对其中的不平衡力偶进行拆分,部分分配给框架;在此基础上文献[10]对框支-剪力墙结构中框支框架承担倾覆力矩进行了分析。不同力学法取矩点不同,轴力法取矩点为底部所有竖向构件竖向轴力绝对值的合力作用点,改进轴力法取矩点为底部受拉剪力墙和受压剪力墙两者中竖向轴力较大者的作用点。力偶法虽未明确取矩点,但分配不平衡力偶到框架时采用梁反弯点,实质上是取各边界梁[3]的反弯点处剪力合力点。此外,还有以结构竖向构件轴向刚心为取矩点[7],以结构平面形心为取矩点[11]等。

抗规法和力学法[6-9]的计算结果差异大,刘付均等[12]基于抗规法可反映框架和剪力墙抗侧刚度比例而推荐采用该方法,并对其在框支-剪力墙结构中框支框架承担倾覆力矩计算应用进行了改进[13]。王雁飞等[14]基于侧向力作用下框架部分总虚内功与结构总虚内功的比值来界定抵抗侧向力的作用占比,以此评价框架的抗侧力贡献,但已不是倾覆力矩比。

框架倾覆力矩的合理计算在评价框架-剪力墙结构及框架-核心筒结构这两种基本结构体系的双重抗侧力体系上至关重要[14-18],对在这两种基本结构体系基础上演化而来的其他结构体系的研究和应用也影响很大[19-20]。

1 倾覆力矩统一解法总结

1.1 柱剪法和梁剪法的表达

根据文献[3-4]的研究成果,结构内部从i0层到n层的局部带支撑的抗弯框架如图1(a)所示,其中边界柱和边界梁分别指与待求局部结构上下边界相连的框架柱和与左右边界相连的连系梁,并将与待求局部结构上下边界相连的支撑和与左右边界相连的支撑分别定义为柱型边界撑和梁型边界撑。则其在水平向作用于各层的侧向规定水平力下框架、支撑和框架+支撑的倾覆力矩,以柱剪法可分别按式(1a)～(1c)计算,以梁剪法可分别按式(2a)～(2c)计算,式(1a)～(1c)及式(2a)～(2c)中各轴力、弯矩、剪力均按图1(b)的约定取正负号。

图1 建筑结构中局部一般框架+支撑的示意(从i0层到n层)

(1a)

(1b)

(1c)

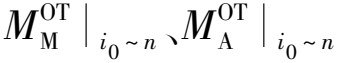
(2a)

(2b)

(2c)

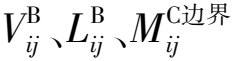
1.2 力学法的表达

统一解法可以基于构件内力的形式来表达,理论上说也可以按力学法的形式来表达。

(3)

式中:Mcj、Ncj和xj分别为结构底层第j根框架柱柱底弯矩反力、轴反力以及该柱相对于取矩点G0的位置变量;m为结构底层框架柱的总根数。

对图1(a)所示建筑结构中局部一般框架+支撑,采用统一解法相应的力学法可仿照文献[3]的规定求解XZ面内该局部结构的倾覆力矩,具体如下:采用矢量形式来表达边界梁边界端、边界柱边界端、梁型边界撑边界端以及柱型边界撑边界端的力和弯矩(不按图1(b)的符号约定),如图2所示,其中各边界端的X坐标也相应给出示意。根据文献[3-4],可推导出力学法下该局部一般框架+支撑的倾覆力矩可按式(4)计算。倘若该局部结构仅在第i0层与底部边界存在边界柱或柱型边界撑,即第i0+1层到第n层均无边界柱和柱型边界撑(即结构无上边界,此时总楼层数即n层),此时该局部一般框架+支撑的倾覆力矩按可由式(4)简化为式(5)来计算。进一步,若该结构中无支撑或只求局部框架的倾覆力矩,则可进一步简化为式(6)计算,式(6)与式(3)相似。

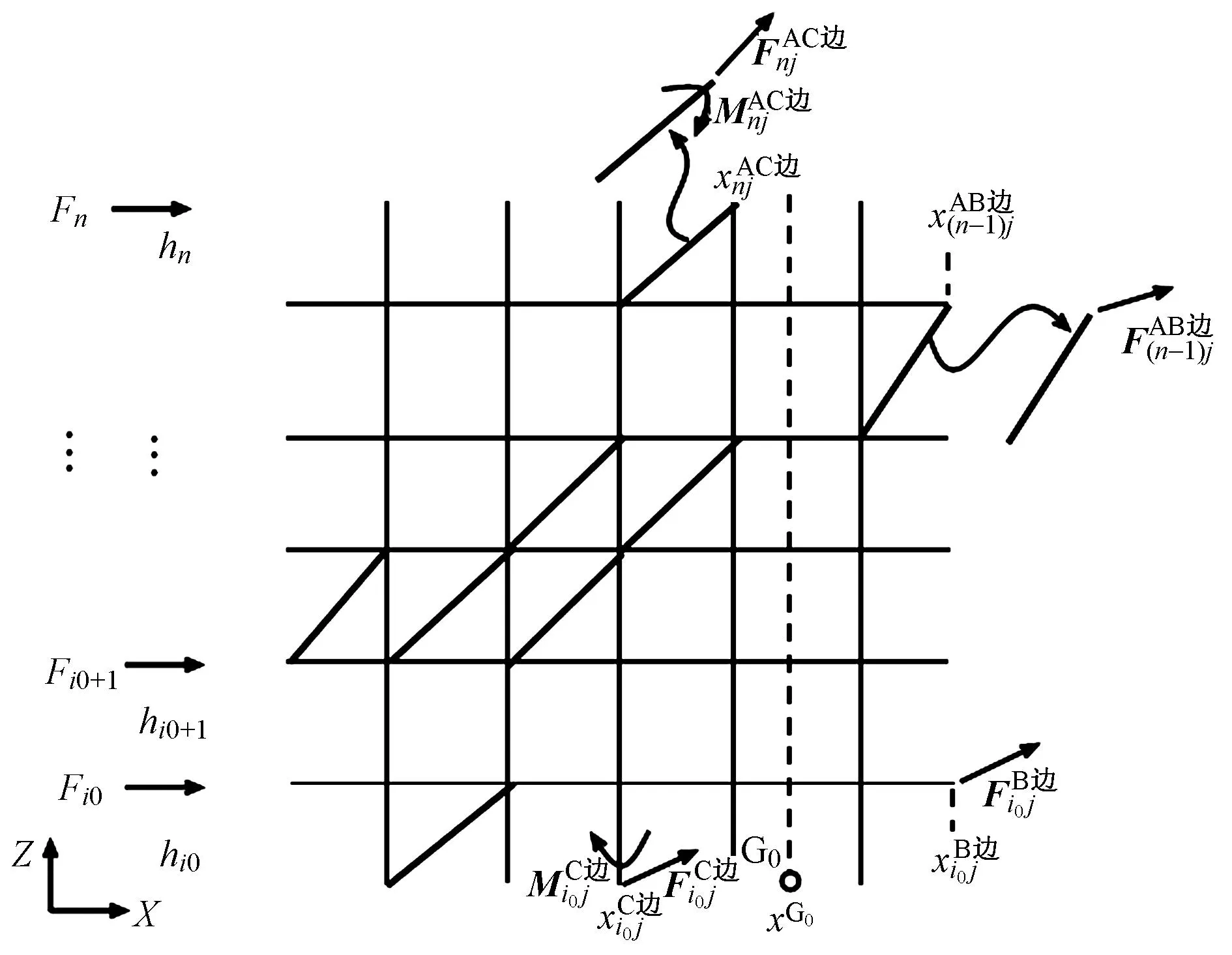
图2 基于力学法求解图1所示建筑结构的局部框架+支撑的相关变量示意(从i0层到n层)

(4)

(5)

(6)

利用力学法准确计算存在前提,即所求隔离体各层边界梁和梁型边界撑不可两端均为边界端,否则会低估或夸大倾覆力矩结果。基于文献[4-5]关于框剪梁(即本文边界梁)的3种定义可知,实际工程中普遍存在框剪梁两端均连至剪力墙的情况,特别是对一向少墙剪力墙结构的少墙方向,力学法计算结果会有较大偏差。这限制了式(4)～(6)所示力学法的应用范围。

对比上述各求解隔离体倾覆力矩的公式,式(1)所示柱剪法和式(2)所示梁剪法均是以隔离体内部构件内力及边界力求解,对其边界构件在结构体系内的位置和形态没有要求;而式(4)～(6)所示力学法则是以隔离体竖向边界力求解,即需有边界柱或柱型边界撑(不可有两端均为边界的边界梁或梁型边界撑)。式(1)所示柱剪法和式(2)所示梁剪法基于结构内部,式(4)～(6)所示力学基于外部但需根据内部边界梁或梁型边界撑来确定取矩点。因此,虽然后者求矩的力学概念更为清晰,但在求取矩点时,仍要深入结构内部,先判定边界梁或梁型边界撑,再计算确定,工作量并未显著减少。而且前者求解过程中更能深入了解结构内部构件的抗倾覆贡献,且可准确考虑边界梁(或梁型边界撑)两端均为边界端的情况。因此,工程实践中,推荐采用前者,特别是式(1)所示的柱剪法。

2 框架承担与分担的倾覆力矩

重力荷载作用下结构中的竖向构件一般是下部构件的轴压力大于上部构件,带来一种下部竖向构件承担着上部构件重力荷载的认识,而这往往是正确的(悬挂结构除外),因而形成工程中惯用术语“力的传递”,从而才有承担的概念,故将该概念延伸到其他荷载作用及地震作用下。

传递这一概念严格说更适合能量,特别是对于地震作用下建筑结构产生的能量响应。此时建筑结构可比拟为平放软绳在端部竖向往复激励下波动能沿软绳向另一端传去,如图3所示。对绳上某一段(相当于建筑结构中某一层),当它振动到波幅最大时其内能、动能最小(相当于楼层水平速度为零且剪力和弯矩最小),当它振动到波幅为零时其内能、动能最大(相当于楼层水平速度响应最大且剪力和弯矩也最大),而不同质点的动能最大值或内能最大值未必相同。

图3 一端往复激励下软绳的波动能传递示意

利用振型分解反应谱法计算结构地震响应,实为评估动力反应过程中最大可能响应,从而将动力问题静力化。而规定水平力进一步将静力化的状态平衡化,从而才可仿照竖向荷载考虑力的传递,才有承担的概念。

对于分担倾覆力矩则更侧重于分,视结构内各构件为平行关系,无需考虑构件间的支承关系,也无需关注力矩的传递。因此,文献[3-5]中论述的规定水平力下框架倾覆力矩是指结构内框架部分所分担(或分配)的倾覆力矩,即本文式(1)、(2)及式(4)～(6),只需考虑隔离体内框架构件的倾覆力矩即可,无需顾及框架和剪力墙之间的支承关系。

但求解框架承担倾覆力矩则必须考虑框架和剪力墙间的支承关系,因为要考虑“力矩的传递和流向”。

对图4所示结构,按式(1)柱剪法求解2层以上隔离体内框架分担倾覆力矩时,将3层框架柱Z1～Z7的分担倾覆力矩均包括进来,这显然不应均被2层框架所承担,从力传递路径最短的角度,2层仅有的框架柱Z8至少是不会承担框架柱Z1的分担倾覆力矩,仅取2层楼面梁L2和3层框架柱Z7的分担倾覆力矩可能更合适。若求解首层框架承担倾覆力矩,由于2层剪力墙Q1支承于框架柱Z9上,Q1的分担倾覆力矩应予计入;而按式(1)求解首层以上隔离体内框架分担倾覆力矩时却未计入Q1的分担倾覆力矩;2层剪力墙Q3支承于剪力墙Q5上,若剪力墙Q5因与水平力方向的夹角α在90°左右而被视为面外受力,则剪力墙Q3的分担倾覆力矩也应计入首层框架承担倾覆力矩中。

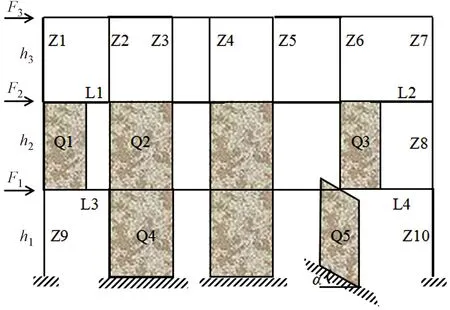
图4 某三层框架-剪力墙结构示意

因此,在倾覆力矩方面,框架承担与框架分担远不相同,准确计算框架承担倾覆力矩相比分担倾覆力矩更复杂。

3 修正的统一解法计算框架承担倾覆力矩

3.1 框架承担倾覆力矩的计算原则

实质上水平力下建筑结构中“力的传递”是主拉应力或主压应力下的应力线轨迹,或者说是应变能等高线所示意的流线,而在构件层次上构件应变能是其弯矩和曲率、轴力和拉压应变、剪力和剪应变各自积分的总和。若只看构件的弯矩,会发现力矩似乎只传至节点区便结束,实则不然。

图5给出了底部固接的一榀规则框架在水平力作用下的弯矩图、轴力图和剪力图。水平荷载下结构整体表现为抗弯和抗剪两大力学特性,抗剪及“剪力流”直观地显示在剪力分布图中,但抗弯及“弯矩流”却很难单独从弯矩图中看出。弯矩图表明水平构件的倾覆力矩以其反弯点为界,以弯矩的形式分别向两侧节点区传递;而轴力图进一步表明,由水平构件传递过来的“弯矩流”汇集在节点区之后转换为框架柱“轴力流”,再以最短路径传至底部支座。因此,水平荷载下结构倾覆力矩的传递在能量上的表现为:从水平构件反弯点处向两侧以弯矩曲率的能量表现形式传递至节点区,转化为竖向构件轴力拉压应变的能量表现形式,再继续往支座传递。

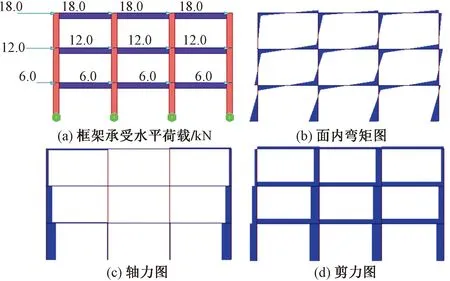
图5 水平荷载下一榀规则框架的内力图示意

水平荷载下结构的倾覆力矩可仅从其弯矩图利用梁剪法或柱剪法求得,而无需查看轴力图[3],但竖向构件的轴力图可理解为倾覆力矩竖向传递的路径。因此,考虑到建筑结构均是底部为支座,在计算水平荷载下首层框架承担倾覆力矩时,可基于以下原则(或约定):从首层各框架柱(包括与所求倾覆力矩方向垂直的剪力墙)出发,从下往上,以相应框架柱向上索引,得到各层该框架柱前后左右楼面梁的反弯点,各层反弯点连线之后形成一条带状子结构,不妨称之为倾覆力矩传递带,该传递带底部即为待求的承担倾覆力矩的框架柱,其承担倾覆力矩即该传递带内上部各结构分担倾覆力矩总和,最后汇总首层各框架柱承担倾覆力矩即为该结构首层框架承担倾覆力矩。

3.2 一般建筑结构中框架承担倾覆力矩的计算

对于一般建筑结构,由于无转换(也无支撑),可微调统一解法中的柱剪法,按式(7)计算i0层框架承担倾覆力矩。

(7)

按式(7)计算时,边界梁仅取与剪力墙面外相交者,原因是剪力墙面内相连的框架梁虽然自身分担倾覆力矩属于框架,但却传递给相连剪力墙,成为剪力墙面内受弯的一部分,因此需予以剔除。

3.3 竖向转换建筑结构中框架承担倾覆力矩的计算

对图4所示结构,求解2层框架承担倾覆力矩时由于存在墙支转换柱,利用式(7)会高估2层框架承担倾覆力矩;而求解首层框架承担倾覆力矩时,又因存在框支转换墙,利用式(7)会低估首层框架承担倾覆力矩。

根据上述框架承担倾覆力矩的计算原则,此时需对式(7)予以修正,结果见式(8)。

(8)

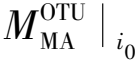
式(8)实质上是对式(1c)所示的柱剪法进行的修正,其中拟框架柱根据待求i0层内竖向构件的性质不同而有所不同:当其位于i0层的面内剪力墙倾覆力矩传递带内时,即使是框架柱也需予以剔除;当其位于i0层的面外剪力墙或框架柱的倾覆力矩传递带内时,即使是面内剪力墙也需予以包含(面外剪力墙不包含,但计入边界梁或边界撑的边界端弯矩)。

对图4所示结构,求解首层和2层的框架承担倾覆力矩时,其上方各层拟框架柱分别如图6、7所示。图6中,因首层剪力墙Q5与楼面梁夹角90°属于面外剪力墙,因此首层剪力墙Q5不视为拟框架柱,但与其相连的两侧楼面梁需视为边界梁,需计入其边界端(图中星号所示)弯矩,剪力墙Q5之上的剪力墙Q3则视为拟框架柱。

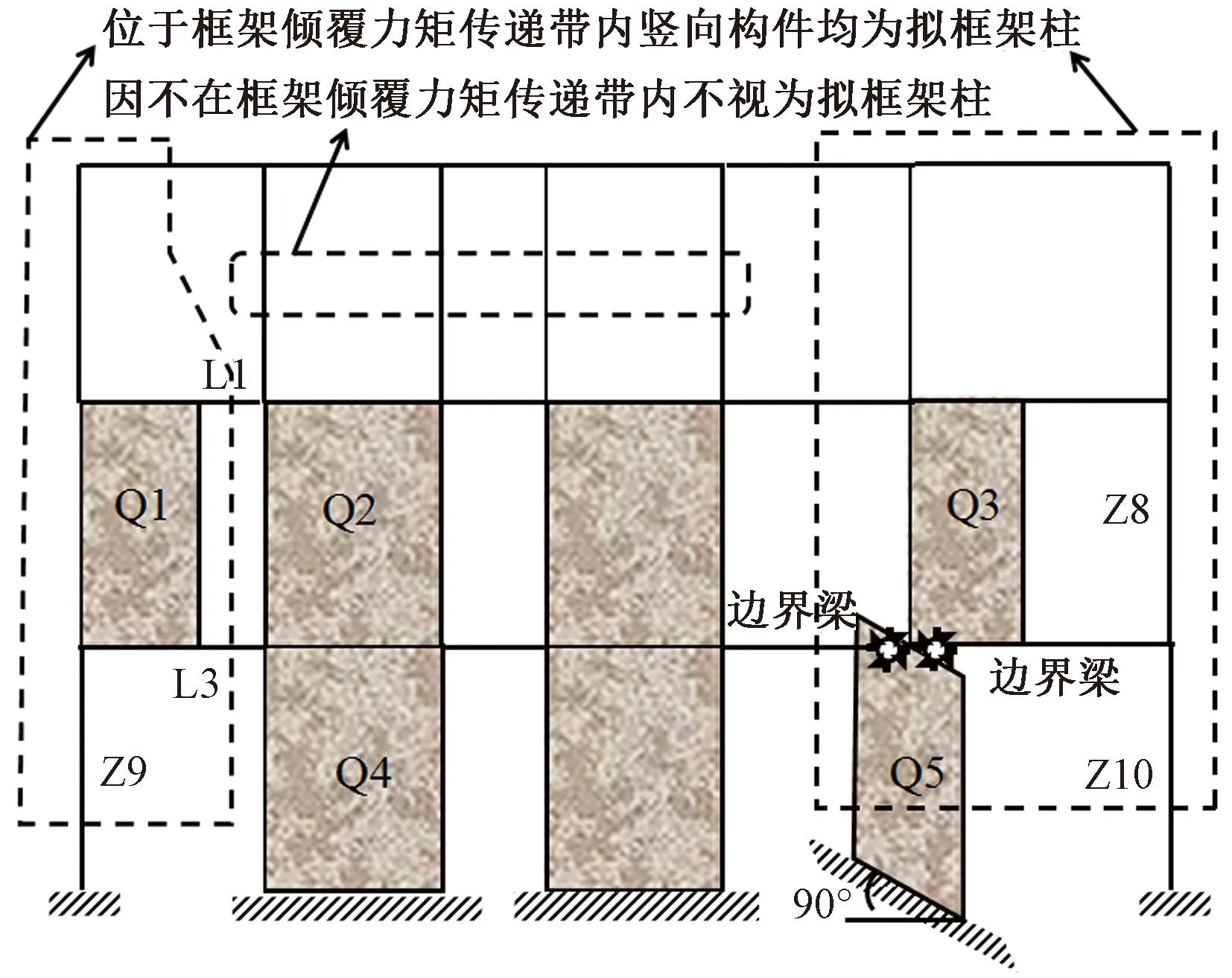
图6 求解首层框架承担倾覆力矩时拟框架柱判别示意

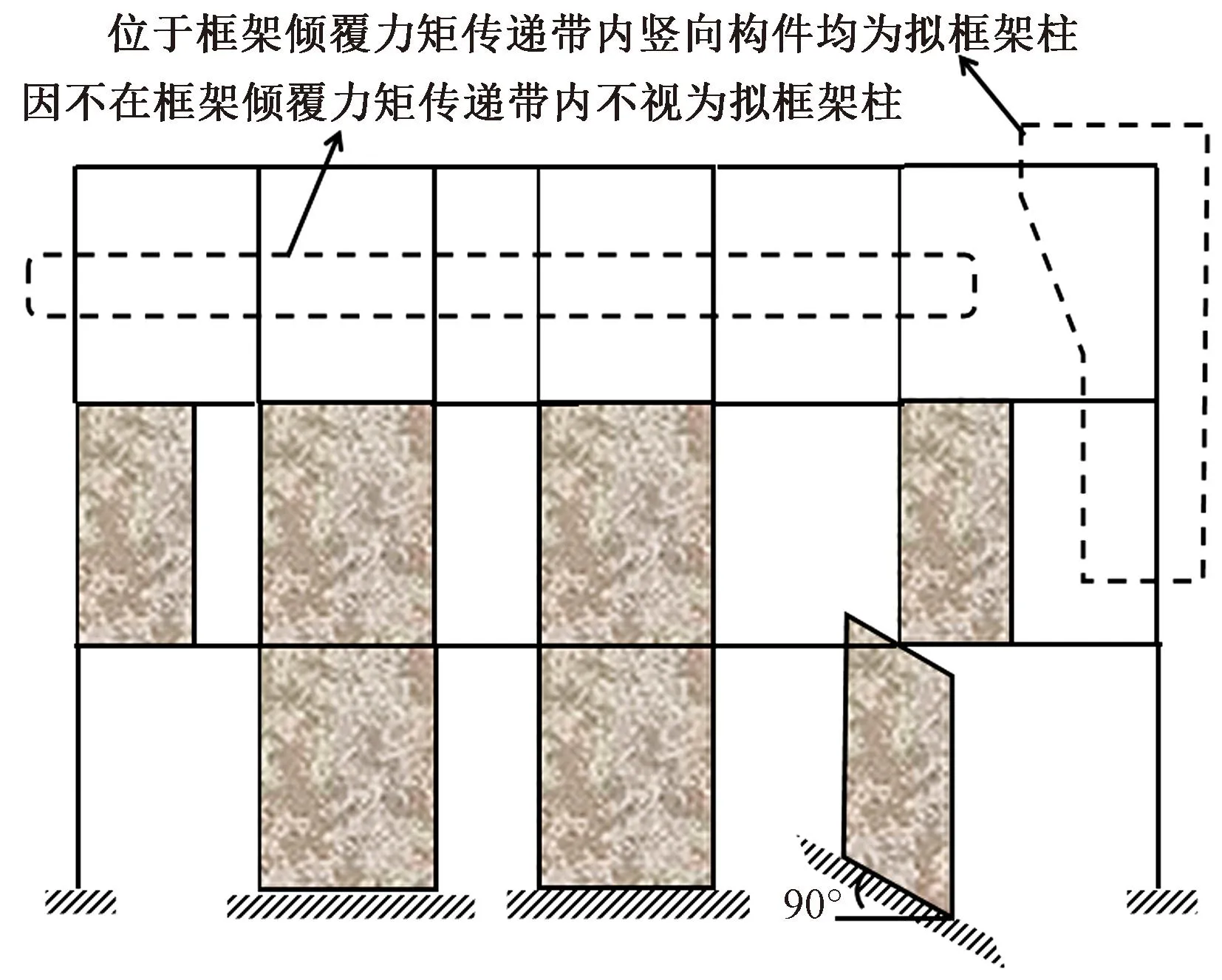
图7 求解2层框架承担倾覆力矩时拟框架柱判别示意

式(7)所示的一般建筑结构中框架承担倾覆力矩的计算式为式(8)的特例。因此,不妨将式(8)记为修正的统一解法,用于建筑结构中框架承担倾覆力矩的计算。

3.4 边界梁有较大拉压力时框架承担倾覆力矩的计算

对图4所示结构可以按图6所示倾覆力矩传递带的划分来计算首层框架承担倾覆力矩,当剪力墙Q1满跨布置而与剪力墙Q2相连,与剪力墙Q4一起形成刀把形剪力墙时,如图8(a)所示,此时边界梁L1和L3已不同于普通边界梁,其存在较大轴向拉压力,该拉压力因该满跨剪力墙协同受力导致,且沿梁长不等。

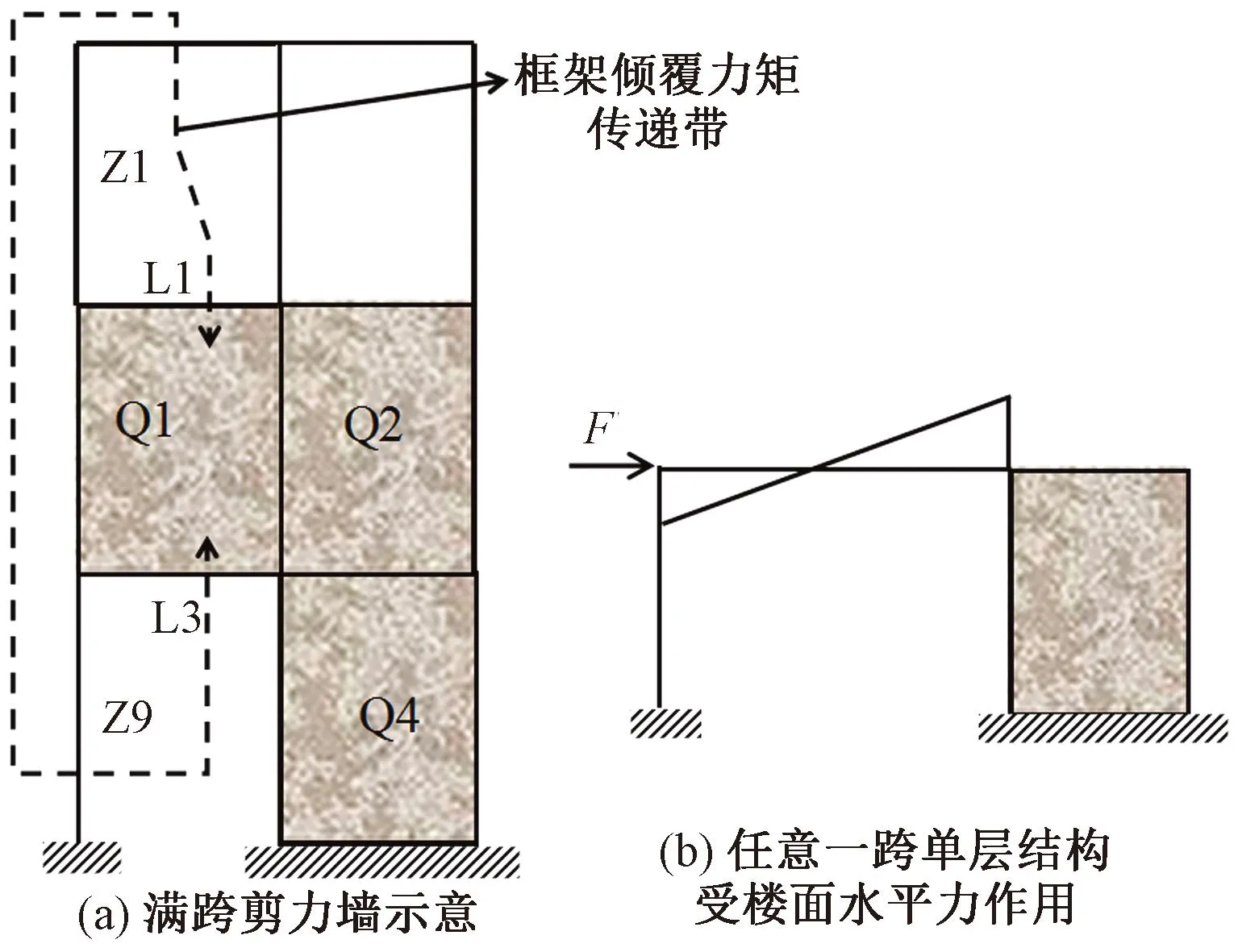
图8 框支墙满跨布置及一跨单层结构受水平力作用示意

此时利用式(8)所示修正的柱剪法来计算时首要问题是确定倾覆力矩传递带穿越剪力墙Q1哪个位置。

对图8(b)所示任意单层单跨结构的楼面梁,无论其两侧竖向构件的刚度差异如何,也无论该楼面梁的刚度如何,水平力下该楼面梁的反弯点在梁长范围内,这是显然的。所以,图8(a)所示的满跨剪力墙Q1的水平向反弯点也在该跨内。可以将梁L1、L3和剪力墙Q1组成一类梁的组合构件,对其左右端的竖向剖面积分得到其左右端弯矩、剪力,继而得到反弯点,该反弯点即倾覆力矩传递带穿越位置。利用式(8)所示修正的柱剪法计算首层框架柱Z9承担倾覆力矩时,宜剔除拟框架柱Q1(当梁L1和L3判定为边界梁时也予以剔除),而增加该梁式受力组合构件的倾覆力矩贡献。

一般情况下,梁式受力组合构件传递给一端框架的倾覆力矩应按式(9)计算。

(9)

式(9)中梁式受力组合构件的楼面集中局部弯矩可根据节点力矩平衡反算得到。如图8(a)所示由梁L1、L3和剪力墙Q1组成一梁式受力组合构件,靠框架端楼面集中局部弯矩数量为2,可分别由框架柱Z1的柱底弯矩和框架柱Z9的柱顶弯矩按节点力矩平衡反算得到。

如图9(a)所示某典型满跨框支墙受楼面水平力作用,其梁柱弯矩分布如图9(b)所示,取梁式受力组合构件并积分得到其弯矩分布如图9(c)所示。该梁式受力组合构件左侧框架柱的弯矩图是曲线状,其剪力沿层高是变化的,因此不可简单地视为拟框架柱按式(8)计算。在文献[4]计算框架分担倾覆力矩时对此类埋置在剪力墙内部或端部的框架柱都不予计入,而将与其相连的楼面梁视为边界梁。根据式(9),该梁式受力组合构件端部积分合力点高度为(12×2×7.2+6×2×3.6)/(12×2+6×2) = 6m,积分结果见图9(c),其传递给左下方框架柱的倾覆力矩为64.0-(16.6+17)=30.4kN·m。

图9 某典型满跨框支墙受水平力作用及其内力图

当梁式受力组合构件两端均传递给框架时,则无需按式(9)修正,按式(8)计算即可。如当图6中的剪力墙Q3和框架柱Z8连为一体而成为满跨转换时,由于其下方两侧的剪力墙Q5和框架柱Z10在该方向均属于框架类,因此无需区分。

该方法可扩展到带伸臂的框架-核心筒结构,只是将伸臂的腹杆和上下弦杆视为梁式受力组合构件,按式(9)来计算其传递给外框柱的倾覆力矩。举例如图10(a)所示某典型带伸臂结构受楼面水平力作用,其梁柱弯矩分布如图10(b)、(c)所示,将伸臂腹杆和上下弦杆视为梁式受力组合构件,其端部积分合力点高度为(20×2×7.2+10×2×3.6)/(20×2+10×2)=6m,积分得到其弯矩分布如图10(d)所示。根据式(9),该伸臂构成的梁式受力组合构件传递给左下方框架柱的倾覆力矩为104.7-(22.2-17.1+29.3-17.5)=104.7-16.9=87.8kN·m。其靠框架侧楼面集中局部弯矩也可根据该伸臂靠框架侧构件端弯矩求得:5.2+2.8-(-8.9)=16.9kN·m。

图10 某带伸臂结构受水平力作用及其内力图

若利用式(1c)所示的柱剪法来计算该伸臂分担倾覆力矩,其结果正好为其内部三根斜腹杆轴力剪力产生的倾覆力矩(经计算为400kN·m)和周边边界梁和梁型边界撑的边界端弯矩之和,结果为400+5.2+2.8+1.4+2.4-(-8.9-5.1)=425.8kN·m,这与将伸臂视作梁式受力组合构件的倾覆力矩(104.7+321.1=425.8kN·m)一致,结果相互印证。

对于建筑结构中的环桁架,其两侧均连至外框柱,所以无需按式(9)所示梁式受力组合构件计算其传递到框架上的倾覆力矩,按式(8)计算即可,只是需将环桁架的斜腹杆视作拟框架柱来计算。

严格意义上,图6所示的非满跨转换的剪力墙Q1也会在梁L1和L3内产生一定轴向拉压力(一般不大),应视作梁式受力组合构件按式(9)计算,否则会高估其传递给下方框架柱Z9的倾覆力矩。对于满跨转换(如满跨框支转换剪力墙)、跨内转换(如框支梁梁内托转、空腹桁架转换等)以及伸臂等均应视作梁式受力组合构件按式(9)计算,且计算时不宜考虑刚性楼盖假定。

综上,对于一般建筑结构(不带转换)、墙支转换结构、框支转换剪力墙结构或带伸臂的结构,规定水平力下某层框架承担倾覆力矩均可结合式(8)所示修正的统一解法和式(9)所示梁式受力组合构件的倾覆力矩计算式来计算。

对于一些复杂结构,可能难以得到倾覆力矩传递带,这时可以近似求解。如,对巨型交叉撑的框架-核心筒结构,求解单根巨型斜撑时难以得到其倾覆力矩传递带,但可以先求得巨型斜撑与外框柱整体承担倾覆力矩,从而得到取矩点,再根据所求单根巨型斜撑的内力求矩。

4 力学法求解框架承担倾覆力矩

式(8)、(9)给出了结构中框架承担倾覆力矩的合理计算方法,同时也可得到采用力学法计算时的取矩点,可在式(5)取矩点定义基础上进行修正,结果如式(10)所示。

(10)

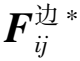
按式(10)得到第i0层框架承担倾覆力矩的取矩点坐标,便可仿照式(5)的力学法来计算第i0层框架承担倾覆力矩。当式(10)中的分母项为零时,需按式(11)式计算MW。

(11)

5 框架倾覆力矩与框架承担倾覆力矩的应用

框架倾覆力矩与框架承担倾覆力矩的差异主要是:对于水平力下的结构总倾覆力矩,框架倾覆力矩是隔离体内框架部分所分担的倾覆力矩,而框架承担倾覆力矩除所求层框架所分担的倾覆力矩外还包括由结构内其他构件传递过来的倾覆力矩。在抵抗水平力倾覆作用上,框架倾覆力矩着眼于结构内总框架部分,视各框架构件之间为平行关系;而框架承担倾覆力矩基于本层框架自身的同时还需考察该框架与周边结构之间的支承关系,可体现框架在结构内所处位置的力学影响。

当结构内框架部分与其余部分之间为弱联系(如图11所示的框剪梁相连)时,框架倾覆力矩与框架承担倾覆力矩差异较小,特别地当框剪梁边界端为铰接时,两者结果相同。但是倘若框架部分与结构其余部分之间为强联系(如图12所示的桁架相连、墙支转换、框支转换以及混合转换)时,两者结果差异很大。

图11 结构内框架与剪力墙之间为弱联系

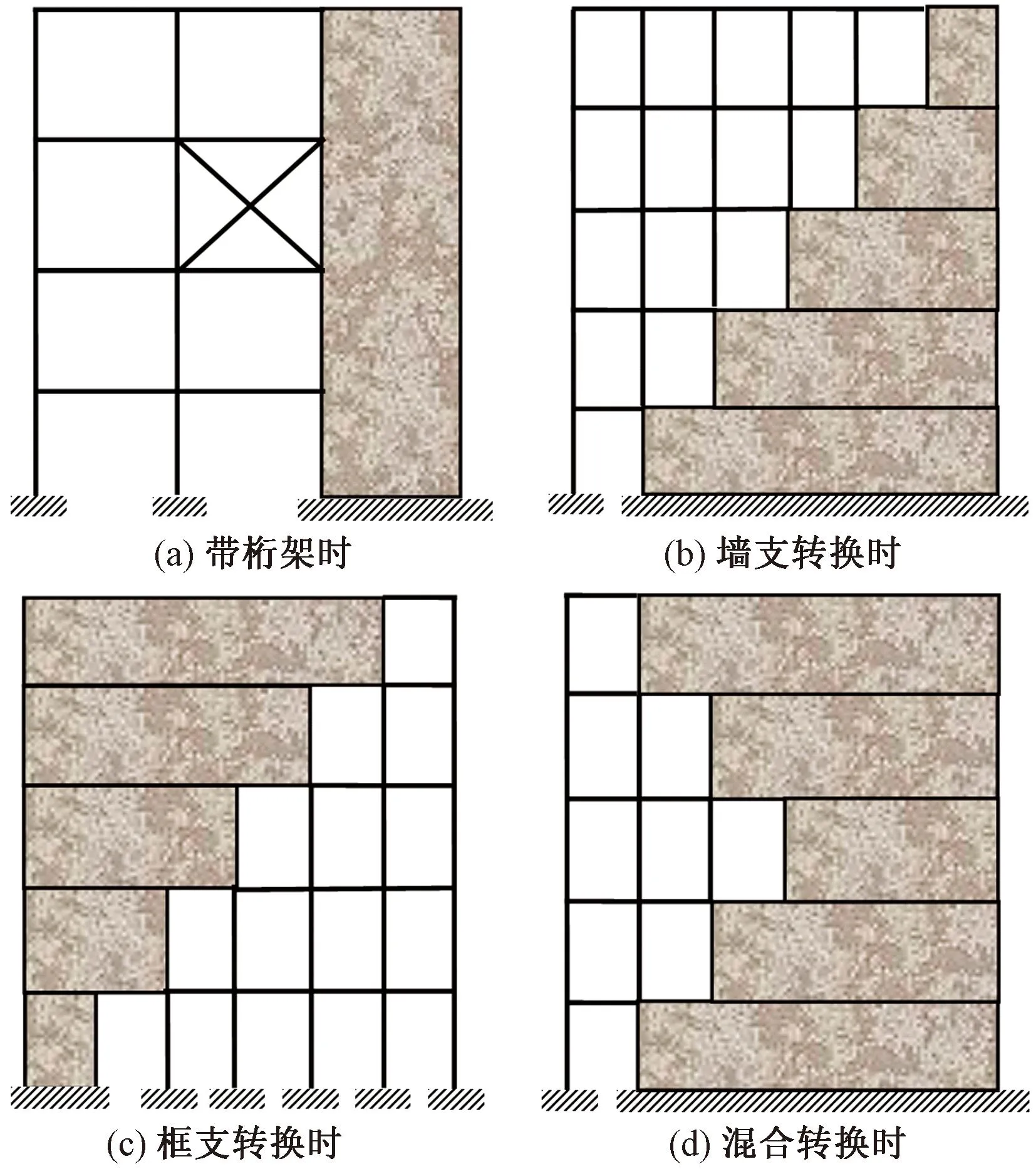
图12 结构内框架与剪力墙之间为强联系

框架倾覆力矩的主要应用是评价结构抗侧特性中框架特性表现的程度如何。对图12(b)～(d),评价此类竖向转换结构的框架特性时应无需查看其框架部分在剪力墙的上方或是下方、左侧或是右侧、或是在剪力墙之间,只要它属于框架类构件,其分担的倾覆力矩则计入框架倾覆力矩中,这是合理的。在高层建筑结构设计中,这一概念用于框架结构、框架-剪力墙结构和剪力墙结构的抗侧结构体系分类[1]。

而框架承担倾覆力矩主要用于评价某框架柱或某部分框架柱在抵抗水平倾覆作用时的重要性,受其所在位置影响很大。由于建筑结构支座在底部,因此一般情况下其在结构底部时重要性大于顶部。

对于图11这类框架部分与剪力墙部分之间为弱联系的情况,由于框架倾覆力矩与框架承担倾覆力矩之间差异不大,导致很长时间以来工程人员误以为按抗规法计算的是框架承担倾覆力矩。而当应用到图12(c)、(d)类结构时,如计算框支剪力墙结构中框支框架承担倾覆力矩,发现抗规法计算结果与概念不符,才疑惑抗规法有误,导致出现了诸多形式的力学法[6-9],其实是混淆了框架倾覆力矩与框架承担倾覆力矩的概念。

抗规法求解的是框架倾覆力矩,而诸多文献[6-9]提出的不同力学法均为求框架承担倾覆力矩,两者并不相同。但无论是求解框架倾覆力矩还是框架承担倾覆力矩,抗规法或现有的力学法均存在不足的地方。文献[3-5]所提的统一解法(式(1)、(2))及其相应的力学法(式(4)～(6))是求解框架倾覆力矩的合理方法;修正统一解法(式(7)～(9))及相应的力学法(由式(5)结合式(10)、(11))是求解框架承担倾覆力矩的合理方法。

6 典型结构案例中框架承担倾覆力矩的计算

为便于说明问题,选取典型结构均为一榀平面结构,按一般建筑结构(取对称框架-剪力墙结构、非对称框架-剪力墙结构)、竖向转换建筑结构(取一对称框支转换剪力墙结构)和边界梁有较大拉压力的建筑结构(取非对称满跨框支转换剪力墙结构和非对称带伸臂结构)三种类别,分别计算和比较不同求解方法下框架承担倾覆力矩及占比。为便于水平荷载的集中输入,在楼面处设置水平平动刚性隔板以模拟实际结构的刚性楼板作用。

6.1 一般建筑结构(非转换类)

取一个对称的3层平面钢筋混凝土框架-剪力墙结构(简称对称框剪结构)进行分析,该结构层高5m,梁截面300mm×600mm,柱截面600mm×600mm,墙厚600mm,混凝土强度等级均为C30,1～3层的水平力分别为100、200kN和300kN,其立面图如图13所示。利用MIDAS Gen进行有限元静力计算,为使得楼层梁与剪力墙连接时转动自由度协调,将楼面梁贯穿剪力墙(设计类软件中往往通过刚性约束实现)。在该对称框剪结构基础上,将右侧框架柱距加大为6m,其余条件不变,得到非对称框剪结构,其立面图如图14所示。

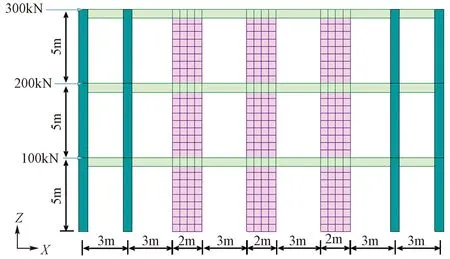
图13 对称框剪结构示意图

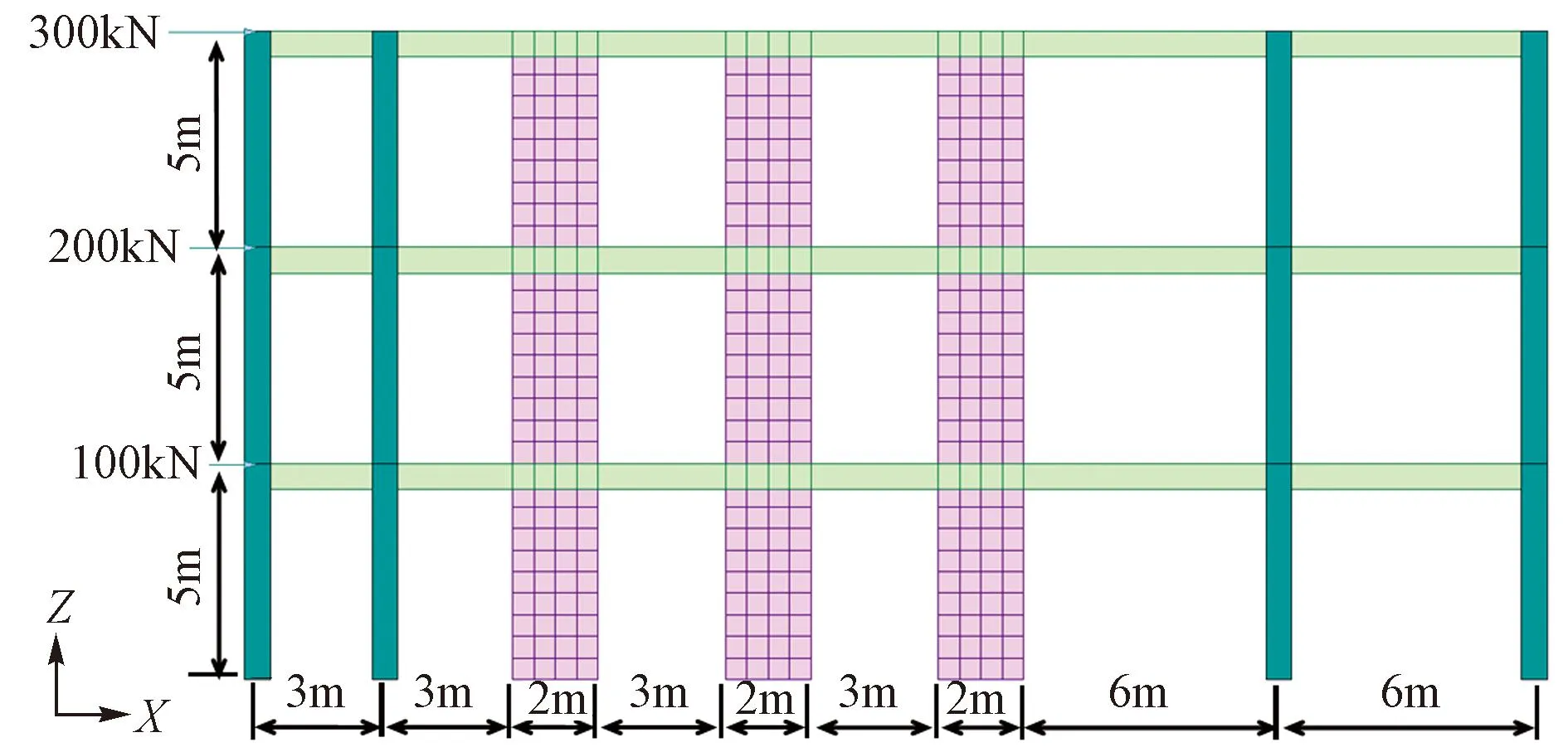
图14 非对称框剪结构示意图

经计算,不同方法下两算例的首层框架承担倾覆力矩及其占比结果分别如表1、2所示。

表1 对称框剪结构首层框架承担倾覆力矩

表2 非对称框剪结构首层框架承担倾覆力矩

按修正的统一解法计算时,由于式(7)所示的柱剪法中的边界梁仅取与剪力墙面外相交者,因此本节算例按式(7)计算时式(7)右端项为零,结果与抗规法相同。

按修正的统一解法所对应的力学法计算时,对于对称框剪结构,扣除项Mw需根据边界梁两端弯矩计算其各自反弯点坐标,再结合其剪力值按式(11)计算,其结果与柱剪法结果很接近;对于非对称框剪结构,需要按式(10)计算取矩点,结果也与柱剪法结果很接近。表明这两种方法结果是一致的。

由对称框剪结构到非对称框剪结构,只是右侧两跨框架的跨度增大,其余均未调整,则框架承担倾覆力矩应略有减小。而按现有的力学法,其框架承担倾覆力矩占比变化较大,且非对称框剪结构各计算方法的取矩点差异也很大。

非对称框剪结构力偶法结果与抗规法接近(占比均为15.1%),而对称框剪结构力偶法结果高达45.9%,其原因是按文献[9]对称结构没有不平衡力偶,因而未计算不平衡力偶分解到框架部分的倾覆力矩,但按其给出的不平衡力偶分解到框架部分的倾覆力矩计算公式来计算,结果并不为零,其值为Mw,扣除之后便与抗规法接近了。这可证明,力偶法与抗规法等效。

6.2 竖向转换建筑结构

从6.1节一般建筑结构算例计算结果来看,按修正的统一解法计算框架承担倾覆力矩与抗规法基本一致,原因如下:一是由于所举案例没有边界梁;二是由于框架承担倾覆力矩传递带上均为框架,没有框支墙或墙支柱的情况。

框支剪力墙结构是一种常见的结构体系,因此在6.1节对称框剪结构基础上,将2、3层内侧框架柱改为非满跨转换的框支墙(墙长2m),其余条件不变,得到对称框支转换剪力墙结构,如图15所示。

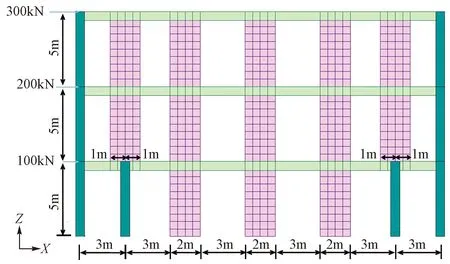
图15 对称框支转换剪力墙结构示意图

经计算,不同计算方法下对称框支转换剪力墙结构首层框架承担倾覆力矩如表3所示,该结构首层框支框架承担的倾覆力矩如表4所示。

表3 对称框支转换剪力墙结构首层框架承担倾覆力矩

表4 对称框支转换剪力墙结构首层框支框架承担倾覆力矩

由于没有梁式受力组合构件,按修正的统一解法计算框架和框支框架承担倾覆力矩时,其传递带穿越各层边界梁反弯点即可,如图16所示。

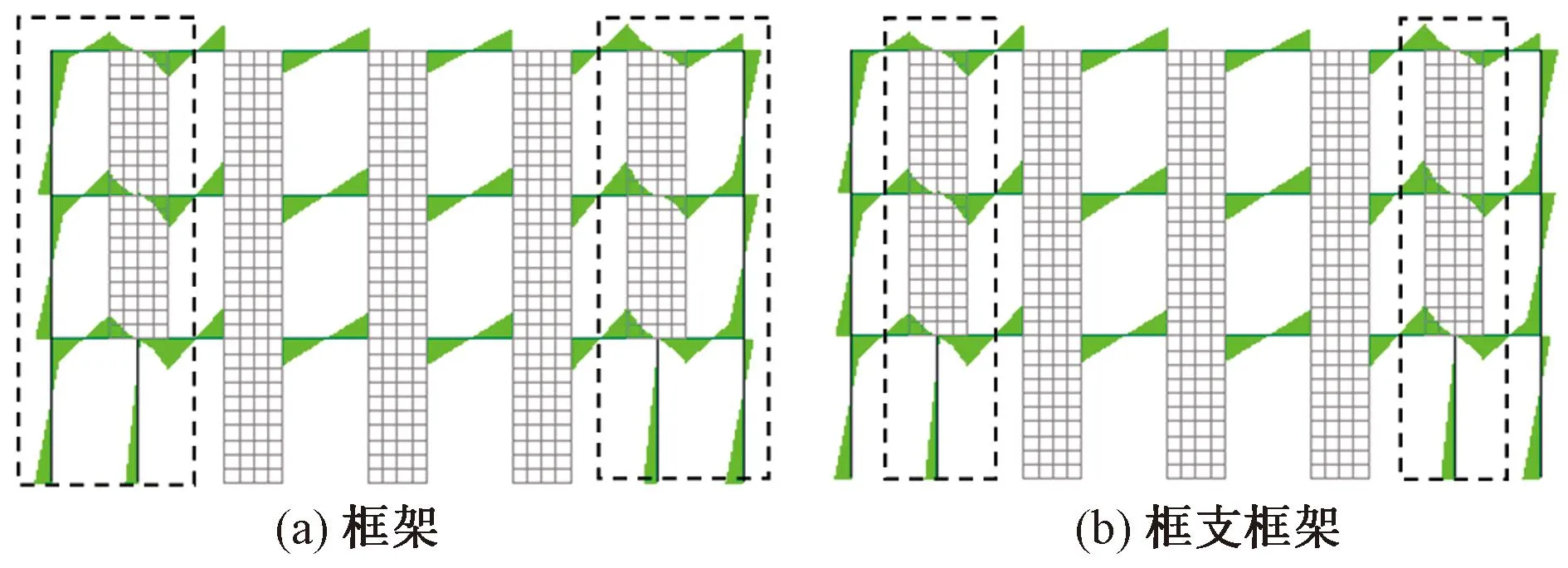
图16 对称框支转换剪力墙结构的框架及框支框架承担倾覆力矩传递带

从表3、4中各计算方法的框架和框支框架承担倾覆力矩的结果来看,差异很显著。由于修正的统一解法计入了倾覆力矩传递带上剪力墙的贡献,其框架承担倾覆力矩占比为29.1%,比抗规法的7.2%高出很多;同样,对于框支框架承担倾覆力矩,修正的统一解法计算结果为22.9%,也比抗规法的1.0%高出很多。这表明,利用抗规法会严重低估框支剪力墙结构首层框架(或框支框架)承担倾覆力矩。

由于外侧普通框架柱轴力远高于内侧框支柱,导致现有常见的力学法计算的框架承担倾覆力矩占比时高达73.4%,而计算框支框架承担倾覆力矩时仅为14.9%。其中,力偶法扣除相应Mw后的结果与修正的统一解法结果相同。

6.3 边界梁有较大拉压力时的建筑结构

在6.1节非对称框剪结构基础上,适当调整,得到非对称满跨框支转换剪力墙结构和非对称带伸臂结构,其立面图分别见图17、18。满跨框支墙墙厚为600mm,伸臂腹杆截面为500mm×500mm。不同方法的非对称满跨框支转换剪力墙结构和非对称带伸臂结构的首层框架承担倾覆力矩结果分别如表5、6所示,由于力偶法未给出非对称情况下带伸臂结构和满跨转换时的计算方法,所以表5、6结果中均未计入力偶法。

表5 非对称满跨框支转换剪力墙结构首层框架承担倾覆力矩

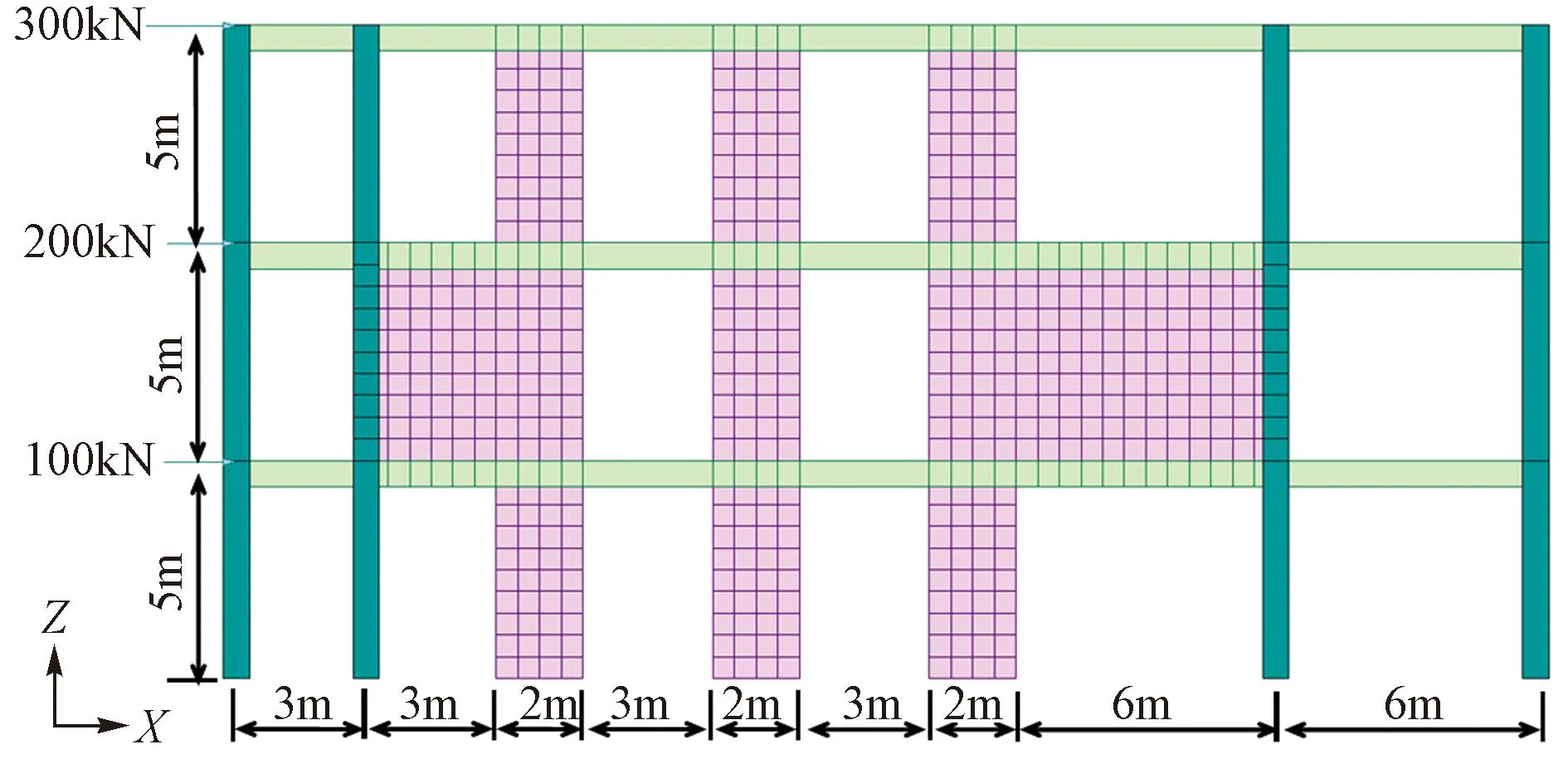
图17 非对称满跨框支转换剪力墙结构示意图

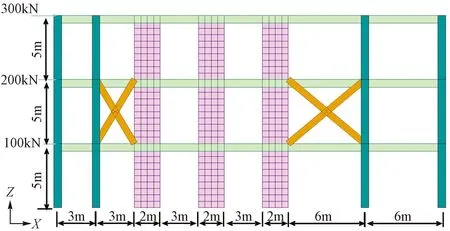
图18 非对称带伸臂结构示意图

对比各种计算方法的两种结构首层框架承担倾覆力矩占比结果,显然抗规法严重偏低,而轴力法首层框架承担倾覆力矩占比超过100%,显然不妥。修正的统一解法下的结果则比较合理,且其柱剪法和力学法的结果也基本一致。

采用修正的统一解法相应的力学法计算时,表5所示的非对称满跨框支转换剪力墙结构的取矩点显著超出结构平面范围;表6所示的非对称带伸臂结构的取矩点甚至在139km之外,其原因是虽然结构为非对称的,但剪力墙的竖向合力基本为零(0.04kN),导致按式(10)计算取矩点时分母项过小,使得取矩点远超出结构平面范围。也正因此,本文不推荐采用力学法计算框架承担倾覆力矩,虽然在修正的统一解法下,柱剪法和力学法计算结果相同。

表6 非对称带伸臂结构首层框架承担倾覆力矩

对两2个算例按修正的统一解法计算首层框架承担倾覆力矩时,需计算各自左右两个梁式受力组合构件。按式(9)计算梁式受力组合构件时,积分高度均为(200×10+100×5)/(200+100)=8.333m,计算得到相应梁式受力组合构件的弯矩值如图19、20所示,图中也给出首层框架承担倾覆力矩传递带。

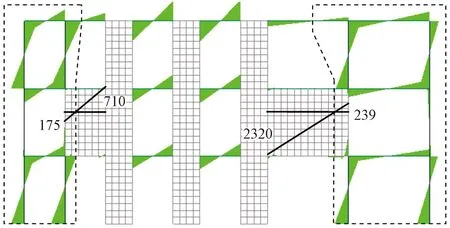
图19 非对称满跨框支转换剪力墙结构框架承担倾覆力矩传递带及梁式受力组合构件积分后的端弯矩值/(kN·m)

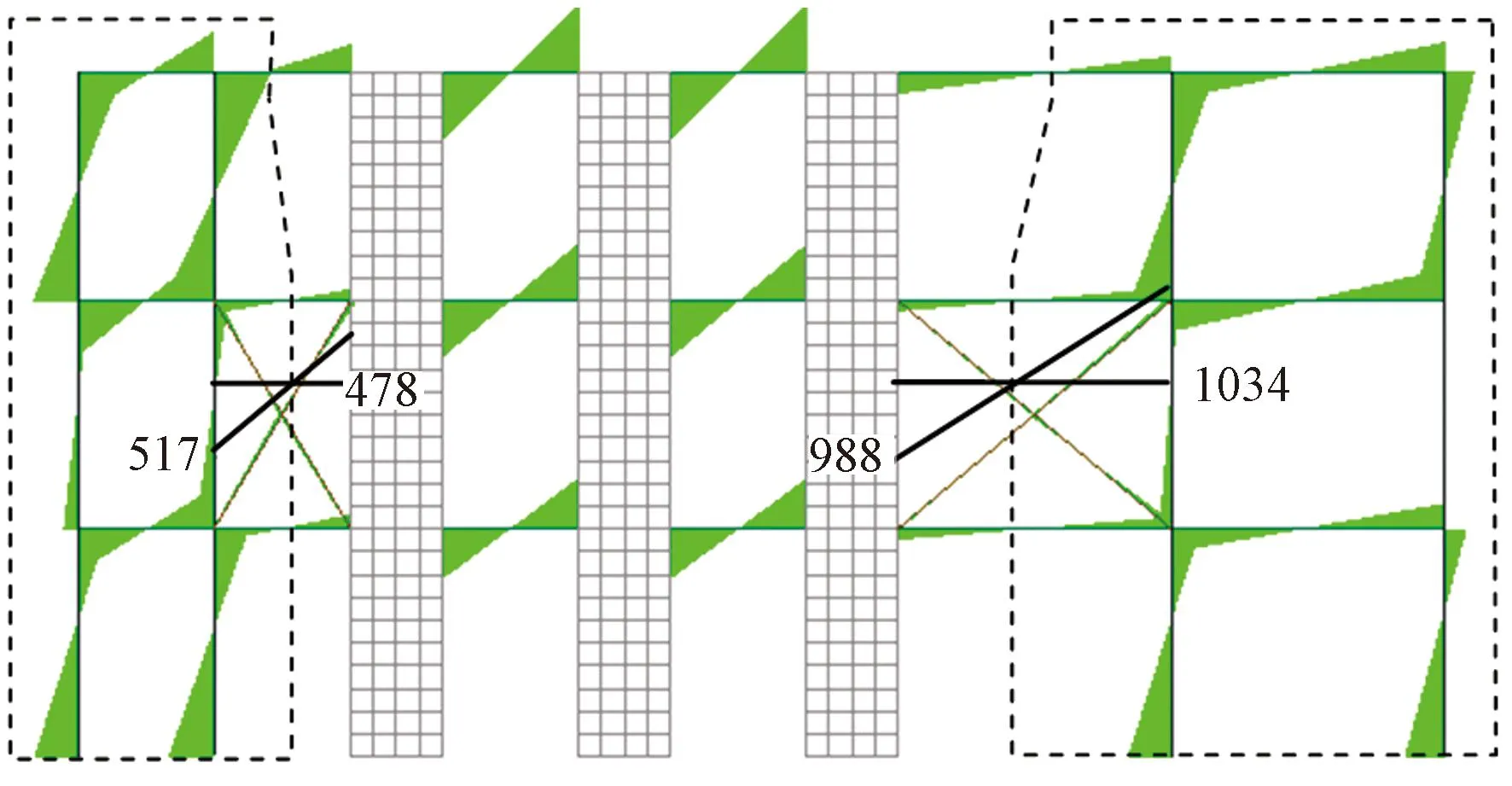
图20 非对称带伸臂结构框架承担倾覆力矩传递带及梁式受力组合构件积分后的端弯矩值/(kN·m)

7 结论

计算框架倾覆力矩的统一解法实为求解框架分担的倾覆力矩,总结并给出其相应的力学法。研究指出框架倾覆力矩与框架承担倾覆力矩之间的差异,并给出求解框架承担倾覆力矩的合理原则,进一步提出求解框架承担倾覆力矩的合理方法。有以下主要结论:

(1)框架倾覆力矩及框架承担倾覆力矩两个概念容易混淆,前者主要应用于评价结构抗侧特性中框架特性的表现程度,可应用于框架-剪力墙结构体系的划分;而框架承担倾覆力矩则主要用于评价结构构件在抵抗水平力倾覆作用下的作用,如用于计算框支框架承担倾覆力矩;建议规范修编时区分此概念,避免混淆。

(2)现有常见计算方法中,抗规法更适于求解框架倾覆力矩,而轴力法、改进轴力法以及力偶法等均为试图求解框架承担倾覆力矩而提出,在本质上与抗规法不同。

(3)统一解法为求解框架倾覆力矩的合理方法,提出的修正的统一解法则是求解框架承担倾覆力矩的合理方法,适用于一般建筑结构(不带转换)、竖向转换的建筑结构(框支或墙支)以及部分复杂结构体系(如满跨框支墙转换结构、带伸臂的框架-核心筒结构)等结构体系。

(4)算例表明,现有常见计算方法(包括抗规法、轴力法、改进轴力法以及力偶法等),在计算框架承担倾覆力矩时,其结果都有或大或小的差异,而修正的统一解法下的柱剪法和力学法计算结果一致,计算结果合理,建议采用。

(5)本文提出的修正的统一解法是基于倾覆力矩传递带概念,而实际结构中难免有些结构体系很难给出其具体构件的倾覆力矩传递带,但往往也可以近似求解。