工艺孔对大截面部分包覆钢-混凝土组合梁受弯性能影响的试验研究*

贾水钟, 刘宏欣, 李亚明, 孙求知, 张朕磊, 钱 桦

(1 上海建筑设计研究院有限公司，上海 200041；2 上海建筑空间结构工程技术研究中心，上海 200041；3 上海世博文化公园建设管理有限公司，上海 200125)

0 引言

部分包覆钢-混凝土组合构件(简称PEC构件)是在型钢翼缘内设置剪力连接件并浇筑混凝土而形成的[1]。PEC构件在预制过程中只需两侧支模,简化了模板要求。翼缘内混凝土的存在可以有效地降低构件整体和局部屈曲的风险,对提高结构的整体承载能力起着重要作用[2-3]。和传统钢构件相比,PEC梁耐火性优良[4-5],且抗弯和抗剪性能显著提高[6-7],在国内外受到了广泛关注。

迄今为止,已有许多研究人员对PEC梁的力学性能和应用进行了研究。Nakamura等[8]发现,PEC梁的抗弯承载力和抗剪承载力分别是传统工字钢梁的2.08倍和2.98倍。He等[9-10]通过试验和数值模拟发现波纹钢腹板PEC梁具有更高的抗剪强度和断裂模数,并提出了其抗剪承载力计算方法。赵必大等[11]通过PEC梁的低周反复加载试验,发现其延性系数在4～6.8之间,耗能系数在2.2左右,具有良好的抗震性能。肖锦[12]进行了T形钢PEC梁在竖向荷载作用下的抗弯承载性能研究,结果显示在竖向荷载作用下,T形钢PEC梁具有良好的承载能力和变形能力。

然而,这些研究大多集中在实腹型PEC梁,且一般均为小跨度PEC梁(跨度<8m),截面尺寸较小(截面高度均不超过600mm)。当结构承受荷载增大,梁跨度较大时,采用普通PEC梁不能够满足重载和刚度的要求,使用大截面PEC梁(截面高度超过600mm)能够有效弥补其不足。为了提高大截面PEC梁的生产效率,实现一次浇筑双面成型,需要在腹板布设工艺(浇筑)孔。为此,本文针对布设有不同形式和尺寸工艺孔的大截面PEC梁的受力性能开展理论与试验研究,目的是得到其破坏形态、承载力、主钢件应变、构件变形及延性,以研究工艺孔对其影响。

1 试验概况

1.1 试件制作

试件依据上海世博文化公园双子山项目实际工程进行设计。双子山项目所采用的构件均为大截面PEC梁,主要参考规程为《部分包覆钢-混凝土组合结构技术规程》(T/CECS 719—2020)[13](简称技术规程)。试件编号分别为LW1(主梁)、LW2(次梁)、LW3(主梁腹板开孔方式1)、LW4(次梁腹板开孔)、LW5(主梁腹板开孔方式2),梁截面高度均超过600mm,定义为大截面PEC梁。主钢件均采用Q355-B钢材,连杆和抗裂钢筋均为HRB400,腹部混凝土强度等级为C30。试件LW1、LW3、LW5的计算长度l0为10800mm,试件LW2、LW4的计算长度l0为7200mm。试件构造立面见图1～6。

图1 试件LW1构造立面图

图2 试件LW2构造立面图

图3 试件LW3构造立面图

图4 试件LW4构造立面图

图5 试件LW5构造立面图

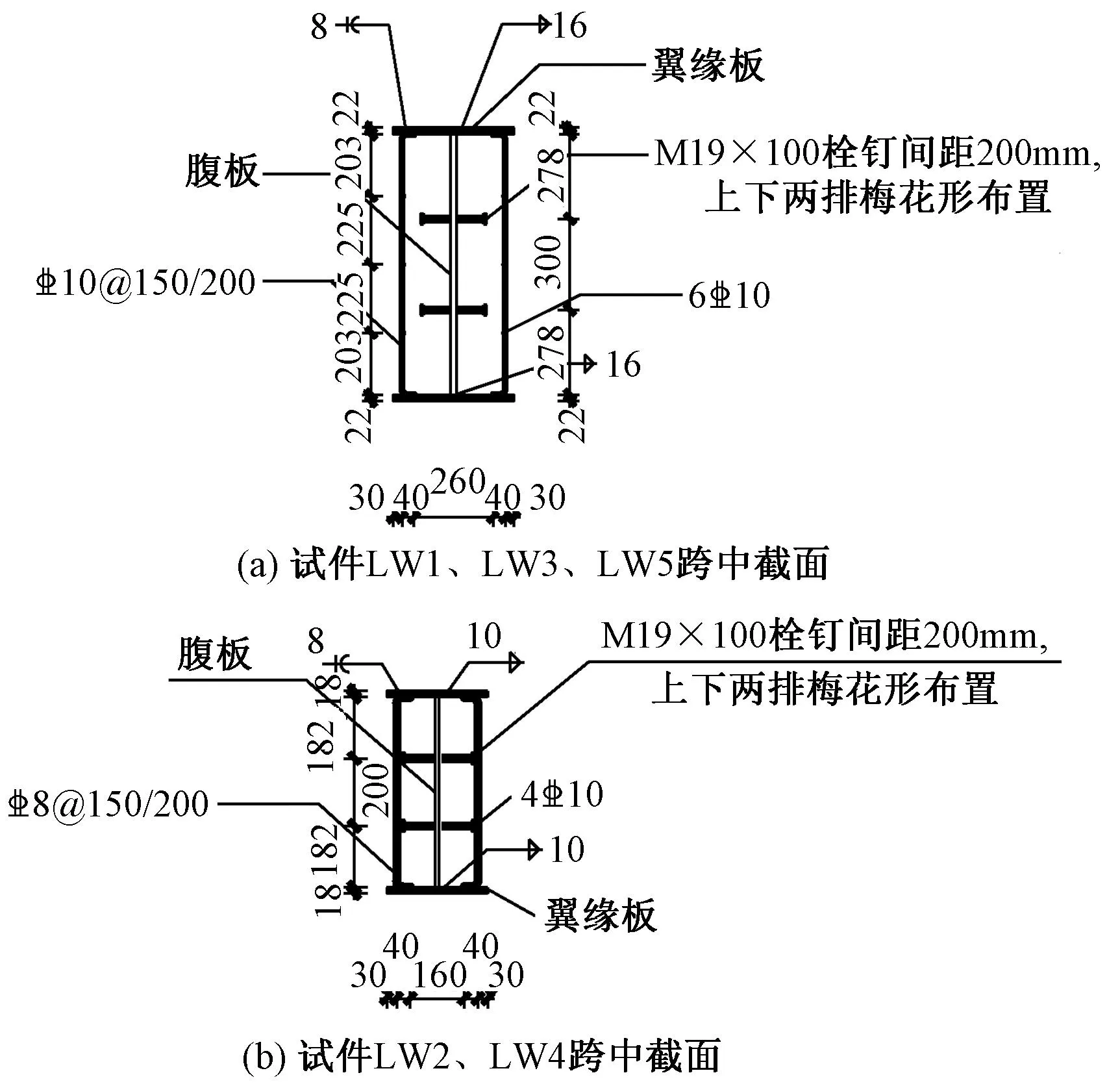
图6 试件LW5跨中截面图

试件基本参数见表1,试件LW3跨中开孔直径为400mm,四分加载点处开孔直径为350mm,其他开孔直径为175mm,其中跨中5个孔洞无混凝土填充。试件LW4跨中开孔直径为300mm;四分加载点处开孔直径为200mm,其他开孔直径为140mm,其中跨中2个孔洞无混凝土填充。试件LW5跨中开孔直径为350mm,其他开孔直径为175mm,腹板开孔起到便于浇筑混凝土作用,孔洞均填充混凝土。试件纯弯段连杆间距为200mm,弯剪段连杆间距为150mm,截面含钢率仅考虑型钢截面。

表1 试件设计基本参数

1.2 材性试验

在同等养护条件下所得混凝土立方体抗压强度为33.1MPa。依据《金属材料 室温拉伸试验方法》(GB/T 228—2002)[14],测得不同厚度t下Q355B钢材的屈服强度fy、极限强度fu、弹性模量E如表2所示。

表2 钢材材料性能

1.3 加载装置及测量内容

试件LW1、LW3、LW5跨度大,截面承载力高,采用双350t作动器实现单调加载,加载点位于三分点处,具体加载装置如图7(a)所示。试件LW2、LW4跨度相对较小,截面承载力较低,采用单350t作动器,作动器施加的竖向集中荷载通过刚性分配梁传递给试验试件,加载点位于1/3计算跨度处,具体加载装置如图7(b)所示。为实现简支边界条件,试件的一端为滑动铰支座,另一端为固定铰支座。

图7 试件加载图

正式加载采用先力加载后位移加载的方式。

试件LW1、LW3、LW5加载时,每级两个千斤顶各加载60kN(约0.05Pu,Pu为梁的极限荷载),加载速度为20kN/min,试件LW2、LW4每级加载为30kN(约0.05Pu),加载速度为10kN/min,达到预估极限承载力的一半(换算截面法计算所得屈服荷载)后,调整为位移加载控制,每级加载5mm,加载速度为5mm/min,加载至构件破坏(考虑千斤顶有效行程,作用点挠度不小于300mm)。试验测点具体布置见图8。

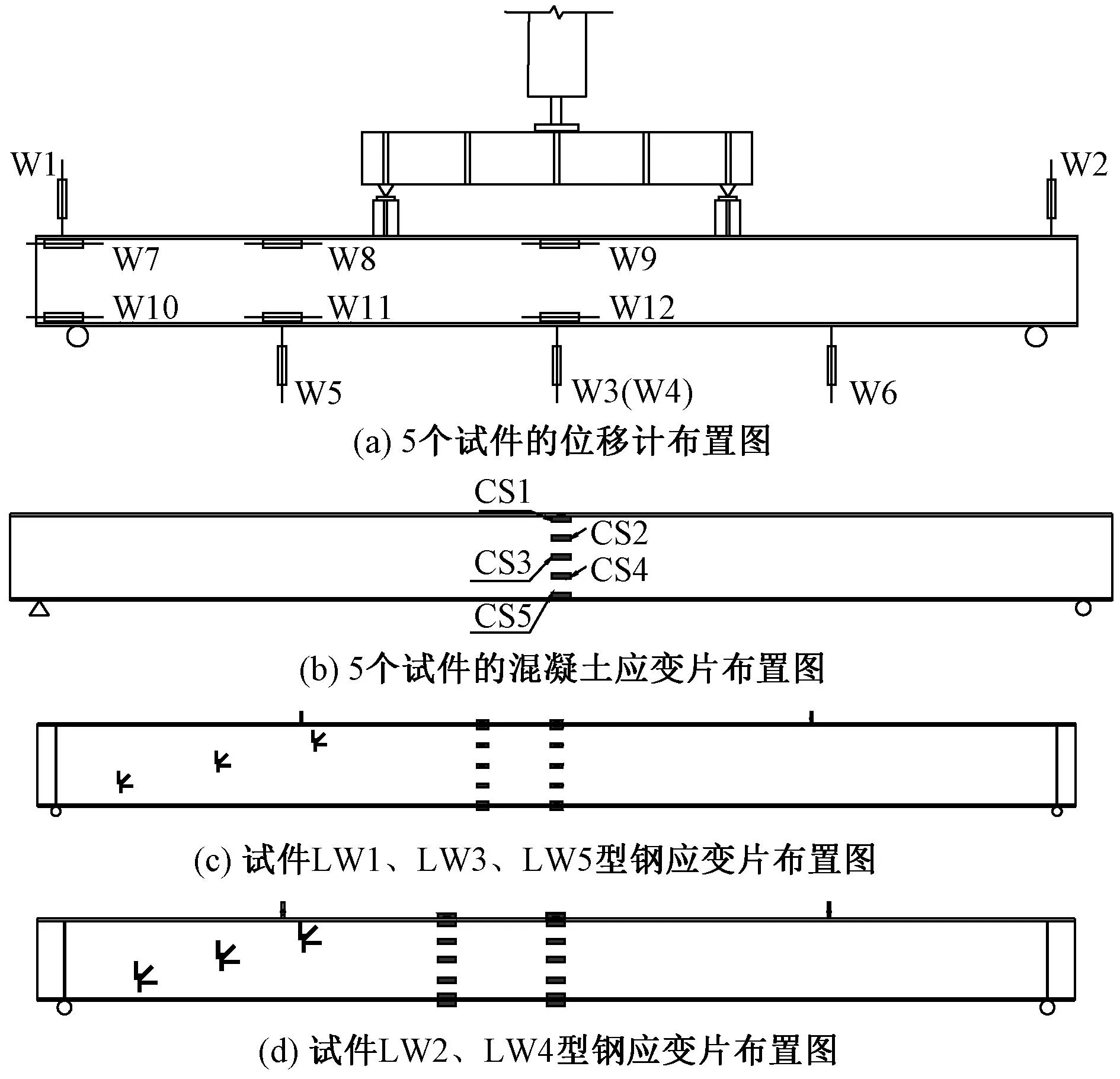
图8 位移计及应变片布置图

2 试验现象

2.1 试件LW1

试件LW1在加载至348.2kN(近似0.11Pu)后进入带裂缝工作阶段,混凝土初始裂缝较多,但裂缝宽度很小,此时跨中挠度为5.35mm(l0/2 019)。加载至1397.3kN(近似0.45Pu)时,跨中最大裂缝宽度达到正常使用极限状态限值(0.3mm),跨中挠度为28.88mm(l0/374)。加载至2640.8kN(近似0.85Pu)时,跨中挠度超过正常使用极限状态限值(l0/200),型钢上、下翼缘达到屈服应变2 700×10-6,跨中挠度为81.62mm(l0/132)。加载至3090.2kN(1.0Pu)时,跨中顶部混凝土表面部分脱落,跨中挠度超过计算跨度的1/50,达到试件破坏条件,停止试验。试件最终破坏时纯弯段如图9所示[15]。

图9 试件 LW1纯弯段破坏形态

2.2 试件LW2

试件LW2在加载至193.5kN(近似0.11Pu)后进入带裂缝工作阶段,此时跨中挠度为4.04mm(l0/1 881)。加载至1276.6kN(近似0.70Pu)时,跨中挠度超过正常使用极限状态限值(l0/200),跨中挠度为48.57mm(l0/156)。加载至1560.9kN(近似0.86Pu)时,两面跨中最大裂缝宽度达到正常使用极限状态限值(0.3mm),型钢上、下翼缘达到屈服应变2 400×10-6,跨中挠度为79.33mm(l0/96)。加载至1813.6kN(Pu)时,跨中顶部混凝土轻微剥落,跨中挠度超过计算跨度的1/50,达到试件破坏条件,停止试验。试件最终破坏时纯弯段如图10所示[15]。

图10 试件LW2纯弯段破坏形态

2.3 试件LW3

试件LW3在加载至339.9kN(近似0.11Pu)后进入带裂缝工作阶段,此时跨中挠度为5.70mm(l0/1 896)。加载至2140.4kN(近似0.69Pu)时,跨中挠度接近正常使用极限状态限值(l0/200),两面跨中最大裂缝宽度达到正常使用极限状态限值(0.3mm),跨中挠度为53.37mm(l0/202)。加载至2463.8kN(近似0.79Pu)时,型钢上、下翼缘达到屈服应变2 700×10-6,跨中挠度为86.63mm(l0/125)。加载至3107.9kN(Pu)时,试件发出异响,跨中顶部混凝土表面部分脱落,跨中挠度超过计算跨度的1/50,达到试件破坏条件,停止试验。试件最终破坏时纯弯段如图11所示[15]。

图11 试件LW3纯弯段破坏形态

2.4 试件LW4

试件LW4在加载至413.9kN(近似0.23Pu)后进入带裂缝工作阶段,此时跨中挠度为10.17mm(l0/708)。加载至1244.5kN(近似0.70Pu)时,跨中挠度超过正常使用极限状态限值(l0/200),跨中挠度为36.82mm(l0/195)。加载至1450.6kN(近似0.82Pu)时,两面跨中最大裂缝宽度达到正常使用极限状态限值(0.3mm),跨中挠度达到79.33mm(l0/96)。加载至1627.5kN(0.92Pu)时,型钢上、下翼缘达到屈服应变2 700×10-6,跨中挠度为117.65mm(l0/61)。加载至1776.7kN(Pu)时,跨中顶部混凝土表面部分脱落,腹板开孔处裂缝较为明显,跨中挠度超过计算跨度的1/50,达到试件破坏条件,停止试验。试件最终破坏时纯弯段如图12所示[15]。

图12 试件LW4纯弯段破坏形态

2.5 试件LW5

试件LW5在加载至646.8kN(近似0.21Pu)后进入带裂缝工作阶段,此时跨中挠度为10.17mm(l0/708)。加载至2284.7kN(近似0.74Pu)时,型钢上、下翼缘达到屈服应变2 700×10-6,跨中挠度超过正常使用极限状态限值(l0/200),两面跨中最大裂缝宽度达到正常使用极限状态限值(0.3mm),跨中挠度为71.17mm(l0/152)。加载至3100.1kN(1.0Pu)时,跨中顶部混凝土表面部分脱落,跨中挠度超过计算跨度的1/50,达到试件破坏条件,停止试验。试件最终破坏时纯弯段如图13所示[15]。

图13 试件LW5纯弯段破坏形态

综上,5个试件首先发生混凝土开裂,随后钢翼缘屈服,最后跨中顶部混凝土表面部分脱落,跨中挠度达到破坏标准。对于试件LW1、LW2、LW5,混凝土裂缝主要集中在纯弯段,且均为竖向裂缝。对于试件LW3、LW4,开孔处传力路径发生改变,除竖向裂缝外,还分布着由孔洞向下侧辐射分布的裂缝,裂缝宽度更大,且孔洞上方混凝土凸起剥落更严重。

3 试验结果与分析

3.1 荷载-跨中挠度曲线

试件荷载-跨中挠度曲线见图14,曲线呈现两个阶段特征:

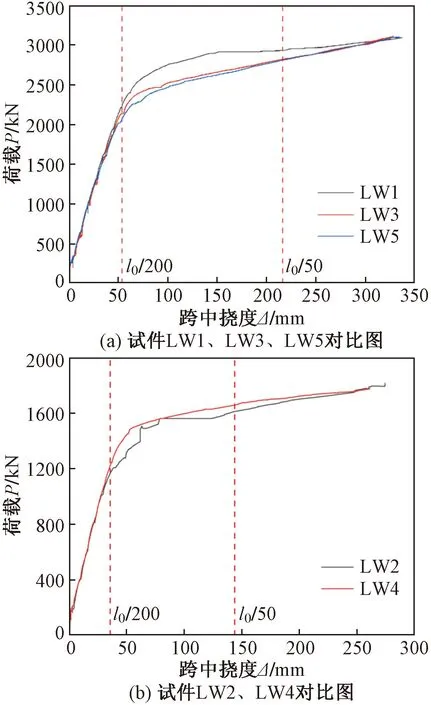
图14 试件荷载-跨中挠度曲线

(1)弹性阶段:在受拉翼缘屈服前,由于主钢件、钢筋对混凝土的约束作用,裂缝开展缓慢且截面刚度未明显变化,荷载-跨中挠度曲线基本呈线性变化。

(2)在受拉翼缘屈服后,试件进入弹塑性阶段,腹部混凝土裂缝迅速发展并逐渐退出工作,截面刚度逐渐降低;荷载-跨中挠度曲线开始出现拐点,呈现非线性变化,跨中挠度变化明显,试件弯曲现象明显;但随着荷载的增加,试件主钢件下翼缘进入应力强化阶段,截面抗弯承载力仍未进入下降段;随着试件主钢件上翼缘屈服,跨中顶部部分混凝土剥落,挠度到达限值,试验停止。

通过对比腹板是否开孔的两组试件荷载-跨中挠度曲线,发现腹板开孔前后试件的初始刚度差别不大,这是因为虽然腹板有开洞,削弱了主钢件截面刚度,但通过混凝土的填充及补强措施得以改善。

试件进入屈服阶段后,试件LW1承载力略高于试件LW3、LW5,但最终破坏时承载力基本相同,试件LW2、LW4曲线的变化趋势差别不大。这表明试件腹部开孔对试件承载力有一定的削弱作用,但整体影响不大,这是因为PEC梁抗弯承载力由主钢件翼缘、腹板、混凝土等多方面承担,但其中腹板作用较小。

3.2 承载力分析

表3 特征点承载力及位移

(1)试件特征点荷载试验值均高于计算值,可以按边缘屈服准则与全截面塑性准则计算承载力。

(2)试件的开裂荷载在0.1Pu～0.2Pu之间,开裂较早,其主要原因可能是混凝土存在初始裂缝,但裂缝的发展满足规范要求,达正常使用极限状态限值时的承载力基本达到了0.7Pu以上。

(3)试件的强屈比范围在1.18～1.30之间,达到屈服荷载后试件仍然具有一定的强度储备。

(4)试验停止时,各试件承载力未发生下降,但刚度下降过大,挠度均达到了l0/50。各试件都表现出良好的延性,延性系数在4.0以上。

(5)相比试件LW1,试件LW3、LW5的屈服强度分别降低了6.0%和8.4%,屈服位移分别增加了5.2%和6.0%;试件LW2、LW4的屈服强度和屈服位移差别不大,说明大截面PEC梁受型钢腹板开孔影响更大。

3.3 应变分析

图15～19为试件LW1～LW5跨中混凝土与型钢沿截面高度的应变曲线,图中h为距离下翼缘高度。由图15～19可见,在达到0.7Pu荷载前,试件LW1、LW3、LW5截面中和轴近似在450mm高度;试件LW2、LW4截面中和轴近似在250mm高度,混凝土与型钢应变沿截面高度符合平截面假定;在达到0.7Pu荷载后,混凝土受拉应变增加,截面中和轴明显上移,腹部混凝土开裂严重,发生应力重分布,截面应变分布呈现一定的非线性。

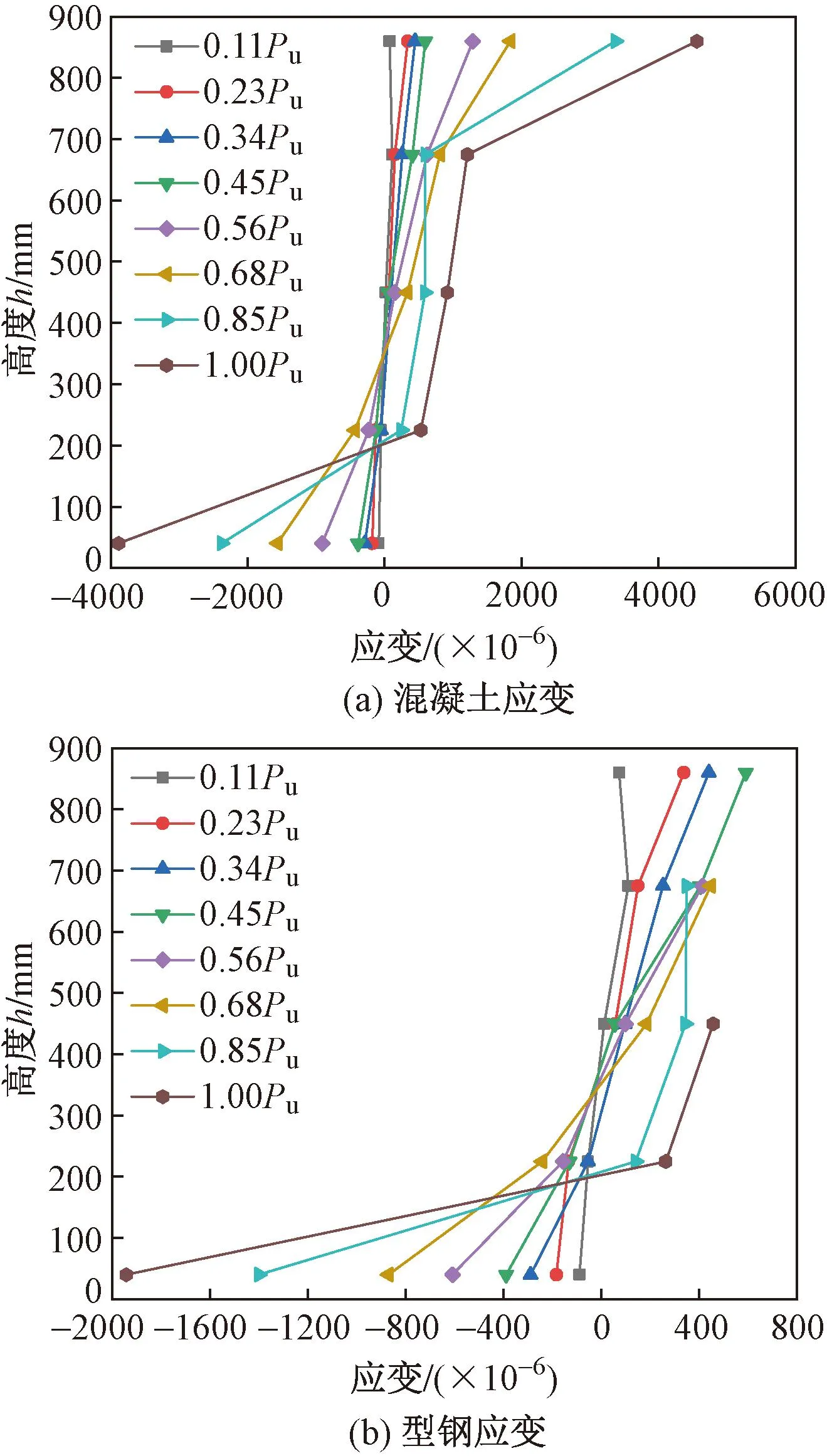
图15 试件LW1混凝土与型钢应变

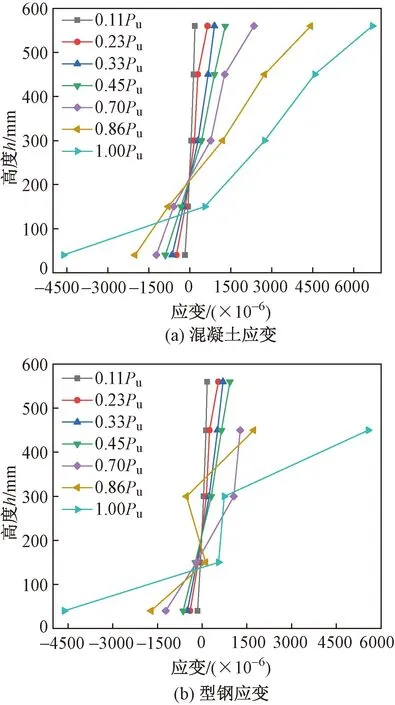
图16 试件LW2混凝土与型钢应变

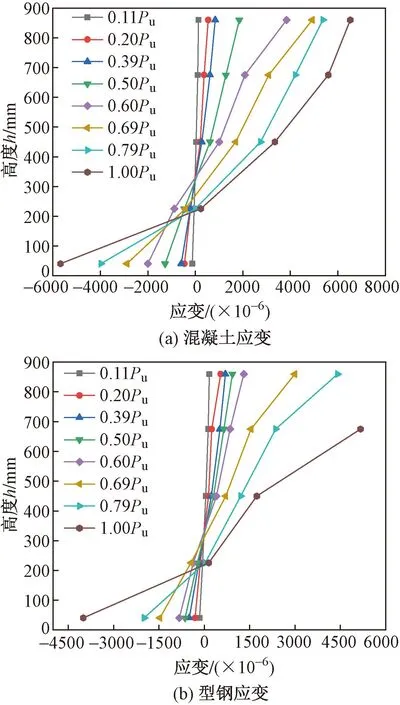
图17 试件LW3混凝土与型钢应变

图18 试件LW4

图19 试件LW5

4 工艺孔大截面PEC梁受弯承载力验算

尽管我国技术规程计算公式考虑了尺寸效应影响, 但由于所依据的试验数据中大尺寸试件数量偏少, 因此重新评价技术规程对大截面PEC梁设计的规定十分必要。

大截面PEC梁截面示意图与等效矩形应力图见图20。试件在达到极限承载力过程中,中和轴不断上移,受压区高度减小。中和轴以上的截面处于受压状态,中和轴以下的截面处于受拉状态,翼缘、受拉钢筋全部达到屈服强度。

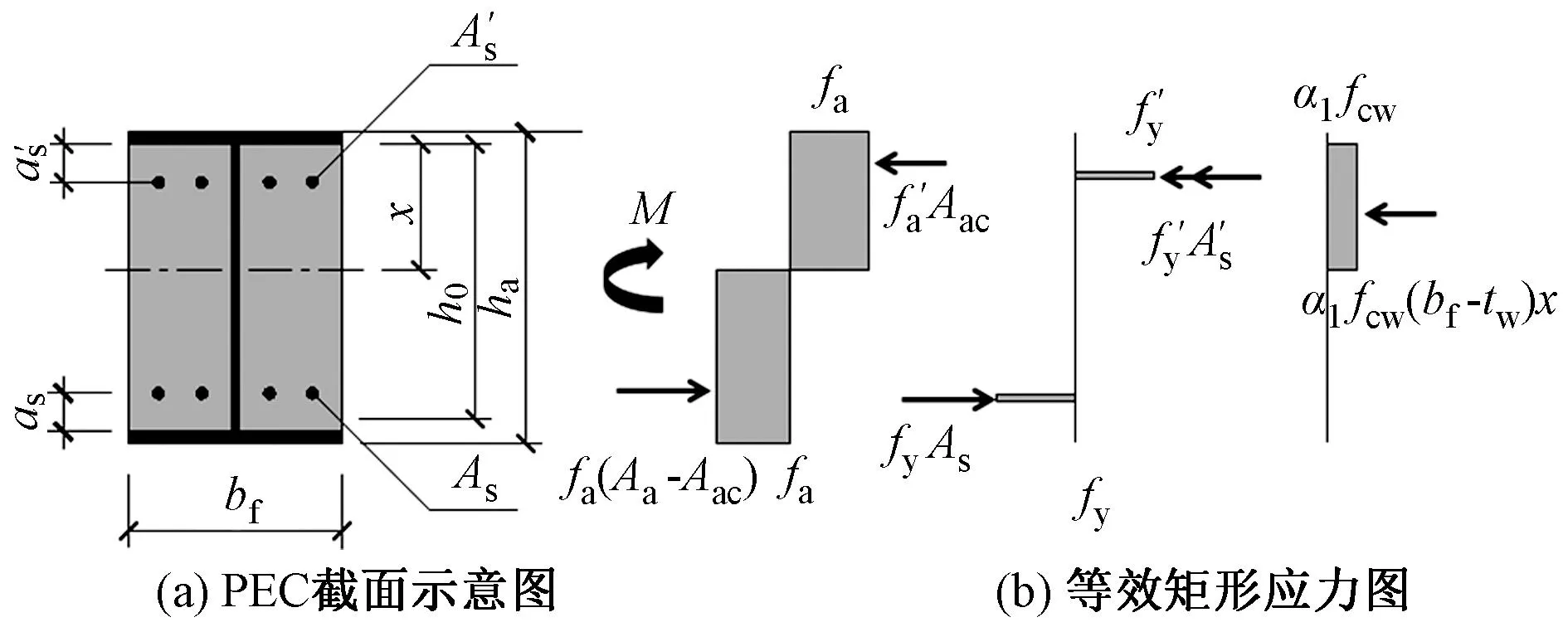
图20 大截面PEC梁截面及应力示意图

大截面PEC梁受弯承载力计算公式见式(1)、(2),所得抗弯承载力计算结果如表4所示。

(1)

表4 受弯承载力计算结果与试验结果比较

fa(Aa-Aac)=0

(2)

其中:

Aac=twx+bftf

由表4可得,试件LW1、LW3、LW5试验结果为计算结果的1.13～1.14倍,而试件LW2、LW4试验结果为计算结果的1.30倍和1.21倍,说明尺寸效应对PEC梁的抗弯性能具有一定的影响,但并不显著,这与已有研究结果吻合[18-20]。计算结果与试验结果吻合较好,故采用上述全截面塑性理论计算开工艺孔的大截面PEC梁受弯承载力是安全合理的。

本文采用平均刚度法计算试件平均刚度B,试件LW3、LW4、LW5在进行刚度计算时已扣除腹部开孔部分。计算大截面PEC梁未开裂的换算截面惯性矩Iucr和大截面PEC梁开裂截面的换算截面惯性矩Icr时,可将主钢件腹部混凝土换算成主钢件腹板,计算公式如下:

Ieq=(Iucr+Icr)/2

(3)

式中Ieq为大截面PEC梁计入受拉混凝土开裂影响的截面等效惯性矩,mm4。

根据计算得到的刚度,可利用结构力学的方法通过刚度求解出试件在0.7Pu时挠度f1,与试验得到的0.7Pu时跨中挠度f进行比较,具体结果见表5,试件的挠度计算公式如下:

(4)

表5 跨中挠度计算结果与试验结果比较

式中:f1为荷载达到0.7Pu时的梁挠度;l0为计算跨度;a为剪跨段长度;P为加载点处所施加荷载;B为试件平均刚度。

根据表5可以看出,理论计算值与试验值的比值均小于1,说明进入弹塑性阶段后,技术规程给出的计算公式与实际试验值存在一定的误差。腹部开孔会导致PEC梁挠度增大,这是因为开孔削弱了截面刚度,刚度削弱需要在实际工程中加以控制,根据工程需要进行设计。

5 结论

(1)大截面PEC梁腹部开孔对试件承载力有一定的削弱作用,但整体影响不大。相比试件LW1,试件LW3、LW5的屈服强度分别降低6.0%和8.4%;试件LW2和试件LW4的屈服强度差别不大。

(2)各个试件延性系数均在4.0以上,大截面PEC梁表现出良好的延性。型钢主钢件、混凝土的应变沿截面高度方向近似呈线性变化,符合平截面假定。

(3)尺寸效应对PEC梁的抗弯性能具有一定的影响。大截面PEC梁抗弯承载力富余度相对较小,但抗弯承载力试验值仍是计算值的1.1倍以上,所采用计算公式安全可靠。

(4)基于折减刚度平均法所得到的大截面PEC梁跨中挠度计算值与试验值存在误差,但不影响正常使用状态极限限值的确定。腹部开孔会一定程度上削弱截面刚度,实际工程中需加以控制。