常州城区承压水影响下基坑抗突涌稳定性判定*

李雄威, 郭严伟, 何 亮, 黄开林, 秦 羽

(1 常州工程职业技术学院，常州 213164；2 常州大学环境与安全工程学院，常州 213164；3 常州工学院土木建筑工程学院，常州 213002)

0 引言

近年来,随着我国社会城市化迅速发展,大型基础设施大量兴建,地下工程日益增多[1-3]。由于承压水的作用,在江苏省南部富水地层中开挖深基坑极易诱发突涌破坏[4-5],造成基坑工程的破坏性事故,轻者造成周围管线和道路开裂,重者可能造成基坑的坍塌。承压水条件下基坑工程的突涌稳定性问题已成为工程界和学术界的研究重点[6-7]。利用数值模拟手段结合现场监测能够较准确地分析承压水影响下基坑抗突涌稳定性[8-12]。张飞等[13]利用有限元数值模拟,分析不同开挖深度下的基坑突涌破坏机制和稳定性,得到了其相应的基坑变形性状,与已有分析方法的对比结果表明:数值分析方法可以分析坑底土体的突涌渐进发展过程,较好地反映内撑式基坑抗突涌稳定性与周围环境变形影响,计算结果更加符合工程实际。Marsland等[14]通过试验揭示了砂土地基中土体渗透破坏现象,表明砂土密实度、围护结构插入深度、基坑开挖深度等是影响临界水头破坏的主要因素,并将地基土体破坏模式分为砂沸、整体顶升破坏和楔形体顶升破坏。胡展飞等[15]认为基坑突涌特征为克服隔水层土体的自重和剪切强度,沿着坑底隔水层土体某铅直面从下往上的滑动破坏,提出了考虑土体内摩擦力和黏聚力的基坑抗突涌稳定性判定公式。杨建民等[16]认为验算承压水影响下的基坑抗突涌稳定性时,应充分考虑上覆土体底部接触面黏聚力和四周抗剪强度的影响,这种影响在某些特定地质条件下可同时起到安全和经济的作用。

本文依托常州地铁2号线青枫公园站深基坑工程,开展承压水影响下基坑开挖的有限元数值模拟,将基坑周围环境变形计算结果和实测数据进行对比分析,验证数值计算的准确性。在此基础上,通过数值计算得出基坑抗突涌稳定隔水层临界厚度值,结合理论判定法得到合理的隔水层临界厚度值。

1 深基坑工程实例分析

1.1 工程概况

本文以常州市地铁2号线青枫公园站深基坑工程为研究背景。基坑开挖深度影响范围内的土层自上而下分布见图1。根据地质勘察报告可知常州区域承压水埋藏较浅、水量较大,与长江水、运河水呈补、迳、排关系,从地铁沿线勘察报告中可知地铁车站深基坑涉及到的第Ⅰ-1层承压水主要埋藏于⑤1、⑤2和⑤3层中,第Ⅰ-2层承压水主要埋藏于⑧1层中,其主要补给源为运河水和长江水的侧向补给,排泄途径为对地表水的侧向补给、人工开采和对其他含水层的越流补给,水量较丰富。第Ⅰ-2层承压含水层平均厚度接近10m,层底平均埋深接近36m,承压水的水头高度可达到20m以上,该承压水对地铁车站深基坑的变形和稳定性影响较大。该基坑工程选用围护墙结合内支撑支护结构方案,设置3道支撑,其中第1道支撑为混凝土支撑,第2、3道支撑为钢支撑,基坑开挖深度为17m、宽22m,围护墙厚0.8m、深31.8m,基坑剖面示意图如图2所示。

图1 工程地质剖面图/m

1.2 现场监测方案

车站基坑监测等级为一级。监测项目和监测点的布置参考《建筑基坑工程监测技术规范》(GB 50497—2019)[17](简称基坑监测规范)、《城市轨道交通工程监测技术规范》(GB 50911—2013)[18]。常州市地铁2号线青枫公园站监测项目见表1。

表1 青枫公园站监测项目

施工现场的地面沉降监测点按远离基坑的方向布设、测点水平间距依次为2、5、5、10、10、15m,地面沉降监测点布置如图3所示。围护墙墙顶水平位移监测点设于地连墙顶冠梁上,观测地连墙顶水平位移,以判断围护结构的稳定性,每个监测点布设在地连墙的墙顶位置,共布置26根测斜管(CX1～CX26),如图4所示,其中计算剖面对应的测斜管监测点为CX7、CX19。围护墙深层水平位移监测点设于地连墙内,每间隔0.5m在墙体布设一个监测点,沿垂直方向布设。

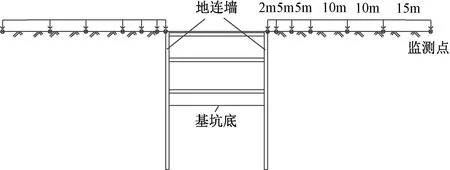
图3 地面沉降监测点布置图

图4 地连墙墙顶位移监测点布置图

2 基坑开挖有限元模拟分析

2.1 有限元模型

根据场地地质勘察报告和室内土工试验(包括三轴固结排水加卸载试验、三轴固结排水剪切试验、共振柱试验、标准固结试验)获得各土层的莫尔库伦和土体小应变(HSS)本构模型参数,如表2所示。其中HSS模型的其他参数为Plaxis软件设定的默认值。

表2 莫尔库伦和HSS模型参数

有限元模型中地连墙采用板单元模拟,抗弯刚度EI=1.4×106kN·m2,轴向刚度EA=2.6×107kN。内支撑采用点对点锚杆单元模拟,第1道混凝土支撑轴向刚度EA=2×107kN,第2道钢支撑轴向刚度EA=8×106kN,第3道钢支撑轴向刚度EA=2×106kN。有限元模型网格如图5所示。

2.2 数值模拟计算结果分析

根据实际基坑的分步开挖施工工况进行数值模拟,计算得到的基坑左侧土体和地连墙水平变形图、土体竖向变形图分别如图6、7所示。由图6、7可知:

图6 基坑左侧土体和地连墙水平位移云图

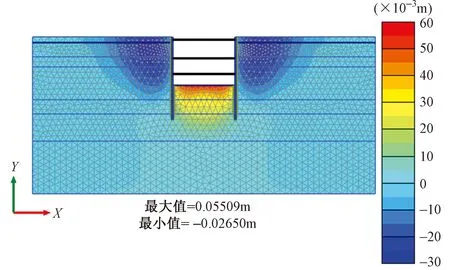
图7 基坑土体竖向位移云图

(1)土体水平位移最大值约为39.0mm,地连墙水平位移最大值约为37.7mm,均出现在基坑底附近。

(2)土体最大沉降值约为26.5mm,出现在距基坑8m附近;土体最大隆起值约为55.0mm,位于基坑中间位置。

2.3 数值模拟与实测数据对比分析

基坑开挖结束后,将墙体水平位移计算值、地表竖向位移计算值与实测数据比较,结果分别如图8、9所示。由图可知:

图8 地连墙水平位移计算值与实测值对比图

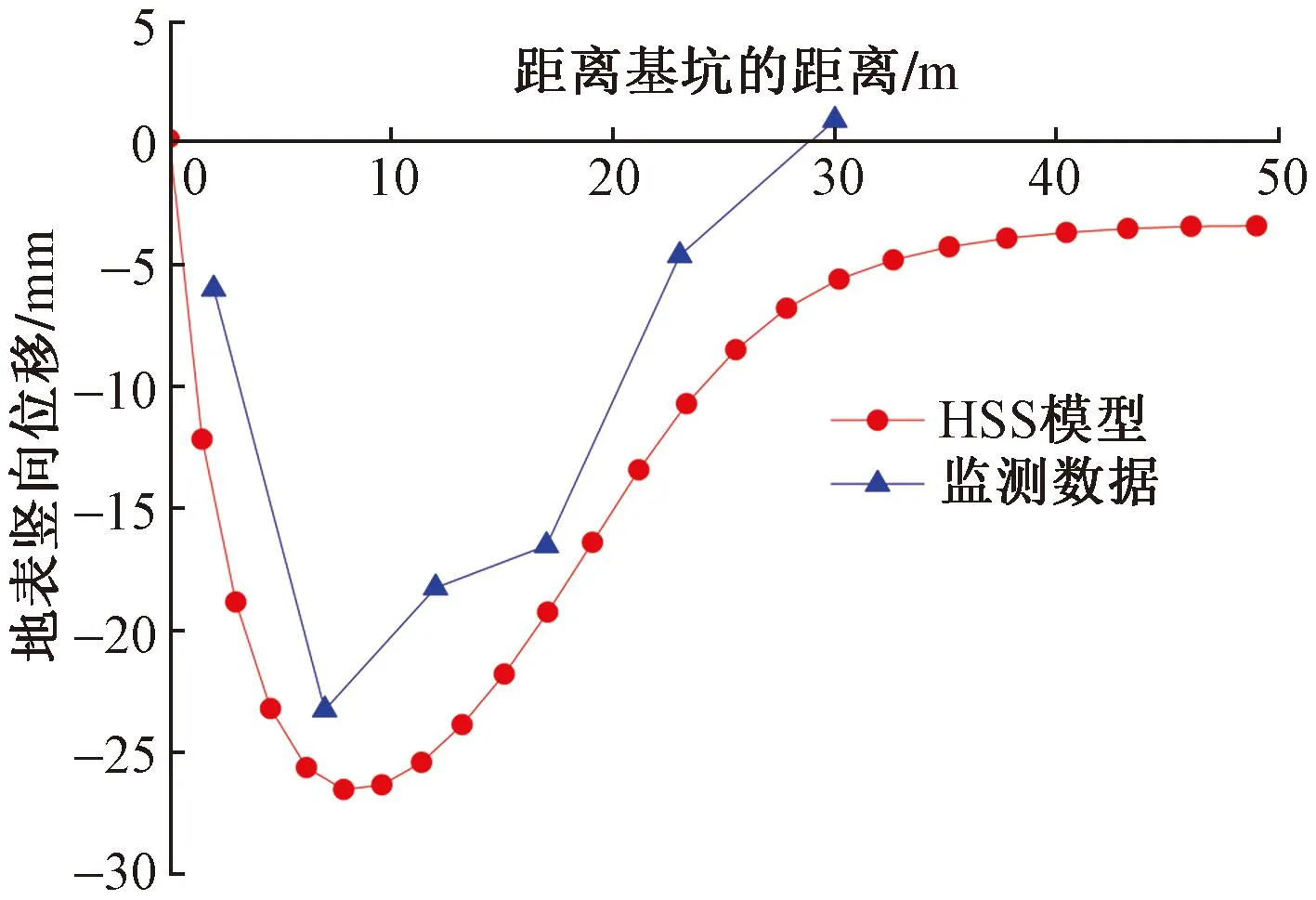
图9 地表竖向位移计算值与实测值对比图

(1)数值模拟得到的地连墙水平位移值、地表竖向位移值与现场实测数据的吻合度较好,两者的差值在合理的范围内,表明基于HSS模型的数值模拟结果和现场实测数据在规律性上较为一致。

(2)基于HSS模型的有限元数值模拟能够预测出基坑开挖变形规律。但需要指出的是:可能由于试验获得的HSS参数偏小(坑底以下土层比实际偏“软”),导致与现场实测数据相比,数值模拟得到的地连墙水平位移最大值位于基坑底部偏下位置。

3 承压水影响下基坑抗突涌稳定性判别分析

3.1 有限元数值模拟分析

为研究承压水影响下的基坑稳定性及其周边土体变形情况,确定最终开挖深度he=14、15、16、17、18、19m的基坑开挖模型,分析随基坑开挖深度的逐渐增加,基坑往突涌状态发展的规律。结果表明:当基坑开挖深度大于19m时(隔水层土体临界厚度为8m),基坑发生突涌破坏。此时的数值计算结果不收敛,基坑底部土体隆起值过大,隔水层表面土体在承压水突涌作用下产生的拉应力超过了土体抗拉强度,从而坑底土体发生了拉裂破坏。基坑开挖深度为19m时,地连墙水平位移图、基坑周围土体竖向位移图如图10、11所示。由图10、11可知:

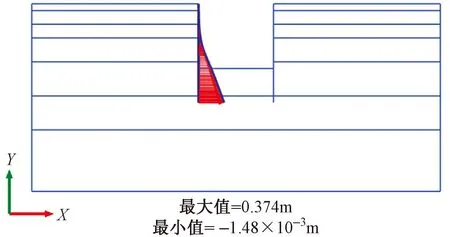
图10 地连墙水平位移图(放大20.0倍)

图11 基坑周围土体竖向位移图

(1)受下部承压水的顶升作用,地连墙上部变形较小,下部变形较大,墙体最大水平位移为374mm,位于墙底部附近;坑底最大隆起值为615mm,位于基坑的中部;地表沉降最大值为238mm,位于距离基坑边缘9m附近。基坑围护结构和周边土体的变形过大,基坑有坍塌的可能性。

(2)基坑即将突涌时,基坑围护结构和周边土体虽未发生破坏,但变形较大,已远超过基坑监测规范规定的理论计算值。且基坑越接近于突涌,地连墙的最大水平位移位置越靠近于地连墙底部。

对比基坑突涌前后土体的剪切应变图,如图12所示。由图可知:与没有承压水情况相比,基坑抗突涌失稳(此时承压水水头为23m,隔水层临界厚度为8m)的数值模拟结果表明:开挖最后一层土体过程中,隔水层厚度较小,不足以抵抗下方承压水的顶升作用,导致隔水层和承压含水层界面产生持续发展的裂缝,并在整个基坑底面贯通发展,使两层土之间脱离,隔水层土体呈现悬浮和隆起状态,即基坑发生突涌失稳[19-20]。

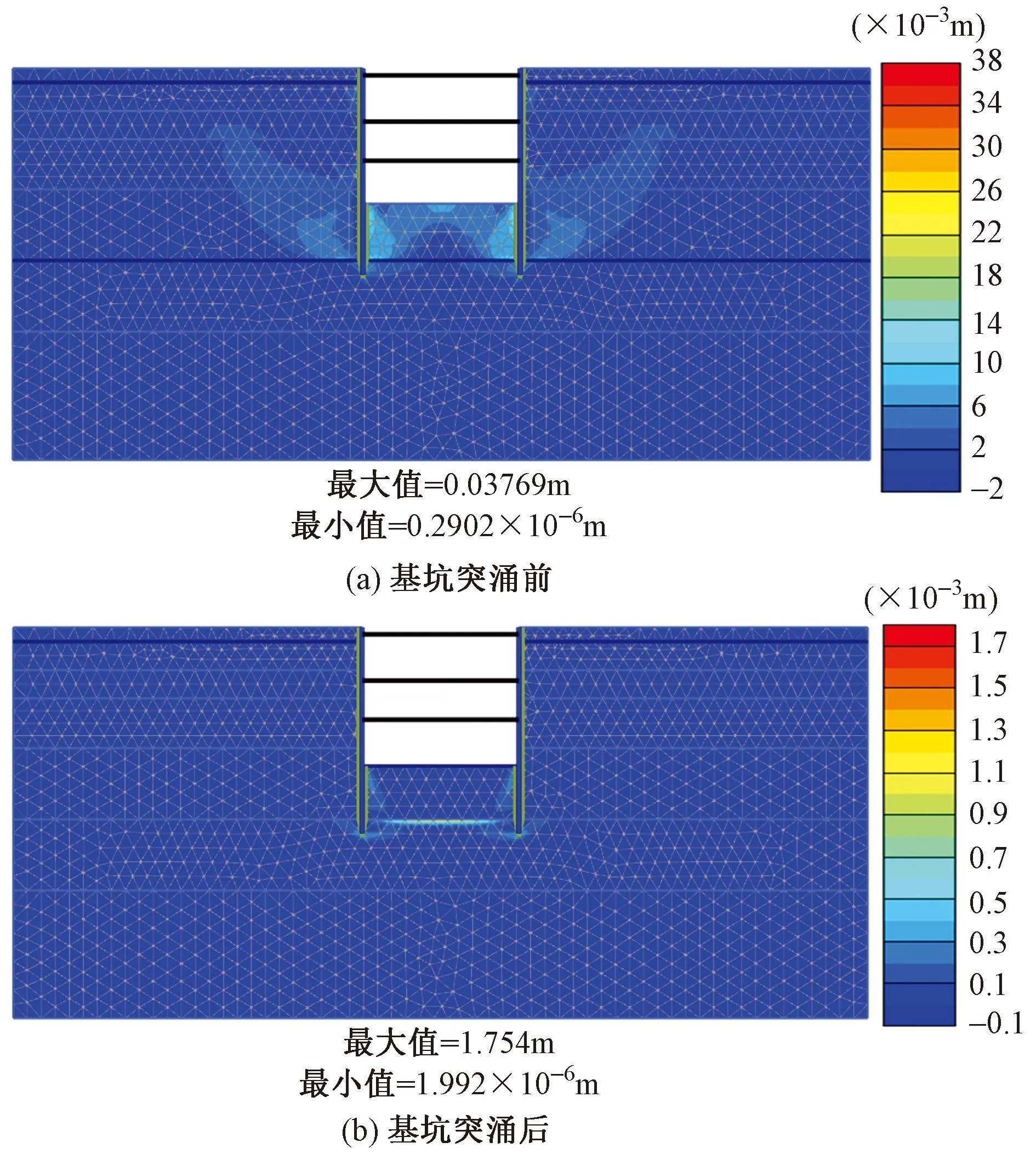
图12 基坑突涌前后土体的剪切应变云图

3.2 数值模拟结果和理论计算结果对比

以不降水条件下的深基坑工程为例,计算参数如下:承压水的层顶埋深为27m,因此基坑开挖深度与隔水层临界厚度Hcr之和为27m。基坑宽度L=22m,均质连续体计算断面宽度B=100m,承压水水头差Hw=23m;基坑坑底隔水层为黏土,其饱和重度γ=20.3kN/m3,黏聚力c=29.7kPa,内摩擦角φ=18.9°,静止土压力系数K0=0.68;突涌稳定安全系数k=1.1。数值模拟方法和其他常见的隔水层临界厚度判别方法对比如表3所示。由表3可得出:

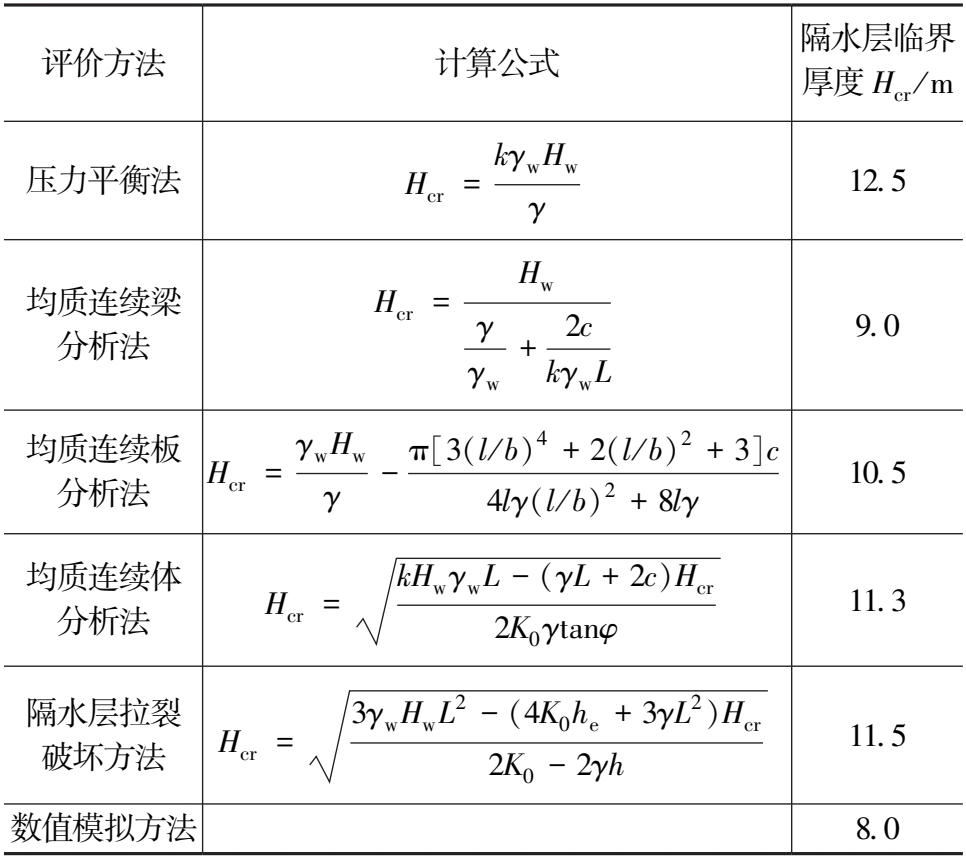
表3 隔水层临界厚度判别方法

(1)压力平衡判别法过于保守,计算得到的隔水层临界厚度也最大。而由于数值模拟方法的判别标准为土体和围护结构强度不发生破坏,判别标准是根据强度判别而不是根据变形判别,因此计算得到的隔水层临界厚度最小。基于强度破坏导致的计算不收敛的数值模拟方法忽视了变形过大导致的工程风险,不够合理。

(2)相比压力平衡判别法,均质连续体分析法考虑了土体的抗剪强度,隔水层拉裂破坏时考虑了土体的抗拉强度,这两种方法计算得到隔水层临界厚度较为接近。说明在承压水影响下,土体内部发生顶升剪切破坏的同时,隔水层表面土体也发生了拉裂破坏。

3.3 基于变形控制的基坑突涌失稳数值模拟判别方法

数值计算得到的基坑失稳隔水层临界厚度值较小,此时基坑周围环境变形值远超过基坑监测规范中规定的基坑变形理论计算值,由此可知,以强度破坏判定承压水基坑失稳的数值计算结果,工程风险较大,应考虑变形控制的基坑失稳数值模拟判别标准。不同隔水层厚度的数值模拟结果与理论计算见表4。由表可知,只有当隔水层厚度不小于8m时的数值模拟结果是收敛的,但数值模拟结果收敛只能说明土体和基坑围护结构强度没有发生破坏,并不代表基坑没有发生突涌失稳。因为地连墙最大水平位移374mm、坑底最大隆起值615mm、地表沉降最大值238mm等变形数值均过大,且远超过基坑监测规范中规定的一级建筑基坑及支护结构的理论计算值,基坑已经发生突涌的可能性较高。因此,以强度破坏导致数值模拟结果是否收敛为基坑突涌失稳的判别标准,隔水层临界厚度取8m是不合理的,工程风险较大。

表4 不同隔水层厚度的数值模拟结果与理论计算值

综合上述,应建立基于变形控制的基坑抗突涌失稳数值模拟判别标准。由于青枫公园站周边环境复杂,车流和人流量较大,且邻近道路和建筑物,周边管线密布。为了安全起见,建议隔水层临界厚度取11.5m,此时,数值模拟结果获得的地连墙水平位移、地表沉降和坑底隆起仅为基坑监测规范建议值的110%、80%和190%,数值在合理的范围内,基坑变形量在工程上是可控的。

4 结论

(1)传统的基坑抗突涌压力平衡判别法计算得到的隔水层临界厚度值偏大,数值模拟计算得到的隔水层临界厚度偏小,此时,基坑围护结构和周边土体虽未发生破坏,但变形远超过基坑监测规范中基坑及支护结构理论计算值。因此,考虑变形控制的基坑抗突涌数值模型更合理。

(2)基坑抗突涌判别定量解析法中,均质连续体分析法考虑了土体的抗剪强度,隔水层拉裂破坏判据考虑了土体的抗拉强度,这两种方法计算得到的隔水层临界厚度吻合度较高。同时表明了基坑抗突涌时,土体内部发生了顶升剪切破坏且隔水层表面土体也出现了拉裂破坏。

(3)结合数值模拟结果和基坑监测规范的基坑变形理论计算值,确定隔水层临界厚度值取11.5m。该方法获得的隔水层临界厚度值,与均质连续体分析法和隔水层拉裂破坏判据计算结果较吻合,进一步表明考虑变形控制的基坑抗突涌数值模型是可行的。