基于模拟退火粒子群算法与小冲杆试验确定材料塑性性能的方法

单应强， 钟继如， 王琼琦， 关凯书

（华东理工大学机械与动力工程学院, 承压系统与安全教育部重点实验室, 上海 200237）

近年来，长距离油气输送管道发展迅猛，管道在高温、高压、易腐环境中长期工作极易出现力学性能下降、脆化、甚至开裂等失效情况。为了保证管道在役期间的安全工作，需要对其力学性能进行测试评价。虽然常用的测试手段如单轴拉伸试验、紧凑拉伸试验等已较为成熟，但其所需的试样尺寸均较大，取样对管道的破坏不可避免，在一些特定的区域部位，甚至无法获得所需尺寸的试样。小冲杆试验作为一种可以在在役管道上，以近乎“无损评价”的测试方法获得了越来越多的关注[1-2]，其试样尺寸一般为ϕ10 mm×0.5 mm，通过对圆形试样中心进行挤压加载直至断裂，得到小冲杆试验的载荷-位移曲线，从而对材料性能进行评价。

目前通过小冲杆试验评价材料的单轴拉伸力学性能已有了很大的进展。在强度方面，韩浩[3]、Zhong[4]、徐亮[5]等分别通过经验关联、数据库和试验标定的逆向有限元方法，获得了材料的屈服强度和抗拉强度。但在材料塑性指标上却鲜有报道，目前从小冲杆试验中获取断面收缩率和断后伸长率，一般采用与小冲杆试样断口厚度和中心最大位移进行经验关联的方法[6-7]，然而由于试验条件不统一，且试样存在尺寸效应[8-9]、几何非线性等问题，获得的经验公式并不能通用。

本文提出了一种基于模拟退火粒子群算法（SAPSO），从小冲杆试验的载荷-位移曲线中，结合有限元模拟获取材料断后伸长率和断面收缩率的方法。通过对小冲杆试验曲线的反演标定，获取材料的Johnson-Cook（J-C）本构模型参数，再利用获得的材料参数模拟单轴拉伸试验，从而得到材料的断后伸长率和断面收缩率。通过与单轴拉伸试验结果对比，证明了该方法获取塑性性能参数的可靠性。且相较于经验关联的方法，本文提出的方法无需进行大量实验，更为高效，成本更低。

1 试验部分

1.1 试验材料

本文使用的材料是X65 和X70 管线钢，试样取自X65 和X70 管线钢弧板。在垂直、平行轧制方向分别切取拉伸试样；沿厚度方向切取小冲杆试样。取样方式如图1 所示。

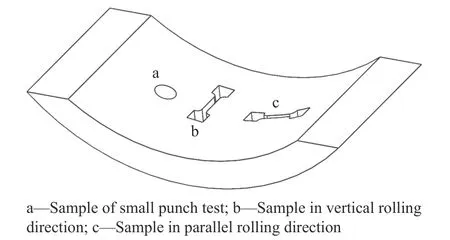
图1 试样切割示意图Fig.1 Schematic diagram of sample cutting

1.2 单轴拉伸试验及结果

单轴拉伸试样选择光滑圆棒，根据GB/T 228.1—2010 进行加工，其标距段尺寸为 ϕ 5 mm×25 mm。试样的具体尺寸如图2 所示。由于材料体积受限，因此每个方向只进行2 次平行试验。采用平行试验取平均值的方法，在型号为MTS Landmark 370.10 的拉伸试验机上进行试验，获取X65 和X70管线钢的强度和塑性性能。

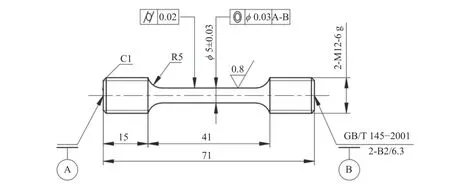
图2 拉伸试样尺寸图（单位：mm）Fig.2 Size diagram of tensile specimen (Unit: mm)

X65 及X70 管线钢的强度和塑性性能如表1所示。从表中结果可知，X65、X70 管线钢不同取样方向上的断后伸长率和断面收缩率较为接近，因此在后文中取不同取样方向上的平均值作为参考。

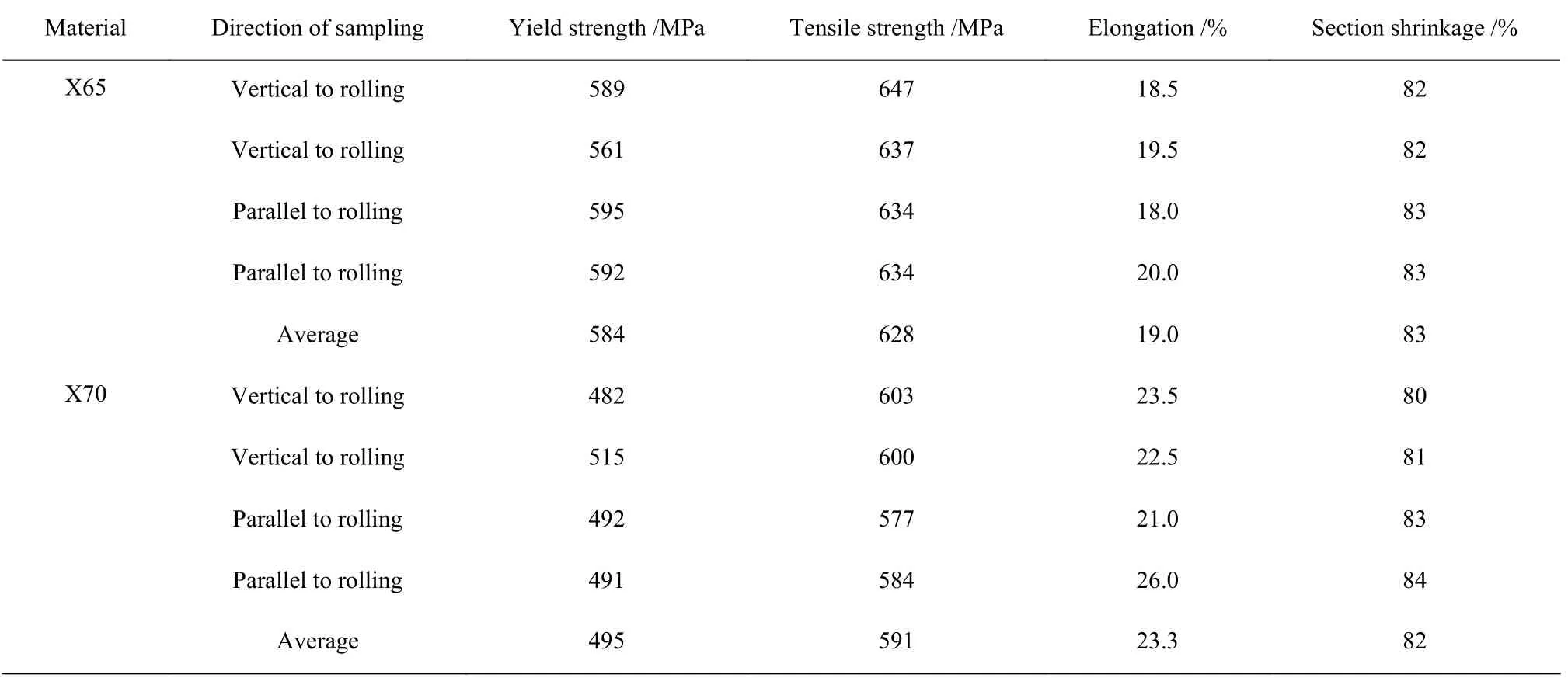
表1 材料单轴拉伸性能Table 1 Uniaxial tensile properties of materials

1.3 小冲杆试验及结果

按照GB/T 29459.1—2012 从弧板中切割小冲杆试样，加工并研磨至 ϕ 10 mm×(0.5±0.01) mm。将研磨后的小冲杆试样在11 μm(1 200 目)砂纸上稍稍打磨，以确保试样表面粗糙度相同。随后，每种材料在SPT-10 型微试样测试机上进行3 次小冲杆试验。本文采用的小冲杆试验装置的示意图如图3所示。小冲杆试验中采用氮化硅陶瓷珠，直径为2.5 mm。下夹具孔径为4 mm 且有0.2 mm 的倒角。加载速度为0.2 mm/min，试样在陶瓷珠的压力下发生变形直至开裂，并通过传感器记录此期间的载荷-位移曲线。图4 所示为小冲杆试验典型的载荷-位移曲线，小冲杆试验的载荷-位移曲线和常规拉伸试验的曲线类似，可分为4 个不同的阶段[7,10-11]：Ⅰ为弹性弯曲变形阶段；Ⅱ为弹塑性弯曲阶段；Ⅲ为塑性强化阶段；Ⅳ为材料损伤软化和断裂阶段。

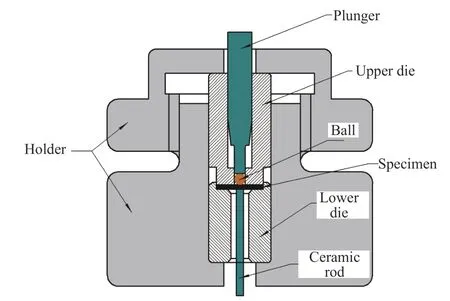
图3 小冲杆试验装置示意图Fig.3 Schematic diagram of small punch test device

图4 小冲杆试验典型载荷-位移曲线及分段Fig.4 Typical load-deflection curves and segments of small punch test

在X65 和X70 管线钢弧板上分别切取3 个小冲杆试样，进行平行试验。其载荷-位移曲线如图5 所示。从图中可以看出，两种材料的3 条平行试验曲线重合度较高，说明制样精良，所测得的载荷-位移曲线稳定可靠。在后文中，采用3 条曲线中的中间条作为目标曲线进行试验。

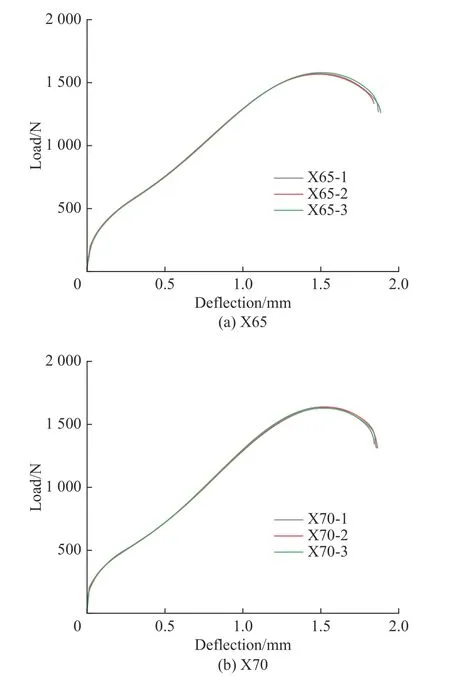
图5 X65 和X70 管线钢小冲杆载荷-位移曲线Fig.5 Load-deflection curves of small punch test for X65 and X70 pipeline steels

2 基于模拟退火粒子群算法的反演方法

2.1 模拟退火粒子群算法

智能算法在有限元模拟的迭代计算当中负责改变输入有限元模型的材料参数，优秀的算法能够以更快的速度和准确度确定材料的J-C 本构参数。粒子群算法由Kennedy 和Eberhart 在1995 年提出[12-13]，其主要特点为信息共享，粒子群不断调整自身的位置、前进方向和前进速度，最终逐渐收敛至最优解。粒子群算法的缺点在于多极值的情况下，易收敛至局部最优解[14]。模拟退火算法由Kirkpatrick 等在1983 年提出[15]，其模拟了固体物质升温、保温和冷却3 个阶段，具有良好的搜索全局最优解的能力。本文采用模拟退火粒子群智能算法作为材料参数迭代的基础。模拟退火粒子群算法的优越性已有多位学者进行测试论述，刘爱军等[16]采用了7 个标准测试函数对模拟退火粒子群算法进行了测试。结果表明在连续单峰函数方面，相比遗传算法，模拟退火粒子群算法搜索精度比其大2 个数量级、且收敛时间是其1/3；在复杂非线性多峰函数方面，对比遗传算法、粒子群优化算法、量子粒子群优化算法、协同粒子群优化算法，模拟退火粒子群算法收敛速度及精度依旧具有明显优势。文献[17-19]的研究结果也均表明模拟退火粒子群的优越性。

模拟退火粒子群算法的原理与粒子群算法基本一致，但在粒子的更新迭代方式上存在差异，其粒子更新法则如下所示：

式中：pi,j为个体极值，下标i、j分别为第j维度空间的第i个粒子， ω 为惯性权重，c为学习因子，r为[0,1]间的随机数， υi、xi分别为粒子的速度向量和位置，t为迭代次数，pg_plus∈pi，按照Metropolis准则接受差解的方法更新粒子[20]：

随着计算的进行，退火温度Tr逐渐降低，算法接受差解的概率也随之下降直至为0，其退火温度的控制由以下函数控制：

式中： γ 为退火系数。

2.2 J-C 本构模型参数的获取

Johnson 等[21]在1983 年对多种材料的本构参数进行了标定，其提出的模型结构简单，意义明确，被大量应用于有限元软件中。本文基于有限元反演方法，利用有限元模拟从小冲杆试验的载荷-位移曲线中确定材料的J-C 本构模型参数。J-C 本构方程分为两部分，第1 部分描述材料的弹塑性变化：

其中： σ 为等效应力，Q为屈服应力，B为硬化模量，εp为真实塑性应变，n为硬化指数，C为应变率指数， ε 为应变率， ε0为参考应变率，m为温度指数，T为材料融化的开尔文温度。

第2 部分描述材料的损伤演化：

其中： εf为断裂应变，Di为材料参数， σ∗为应力三轴度。J=1 时，材料单元发生损伤演化， Δε 为塑性应变增量。当单元发生损伤演化时，还需确定材料的刚度退化参数Dc。

对于准静态的室温小冲杆试验，不考虑应变速率及温度的影响，J-C 本构方程可简化为以下形式：

因此需要确定的J-C 本构模型参数分别为：Q、B、n、D1、D2、D3、Dc。为了求解方便，加快求解收敛速度，将以上未知参数分为塑性参数组和损伤参数组，对其依次进行迭代提取，并假定D1=0 。其中塑性参数与小冲杆试验曲线中的Ⅰ、Ⅱ、Ⅲ阶段相关，损伤参数与Ⅳ阶段相关，因此在迭代对比时采用不同区段的曲线。根据曲线趋势，弹塑性参数对比段选用位移0～1.2 mm 间的曲线，损伤对比参数段则为位移从1.2 mm 至曲线末端。其具体分段对比如图6 所示。

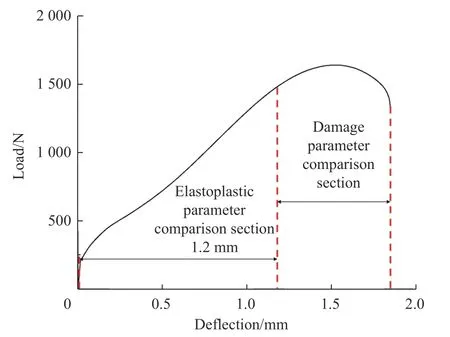
图6 参数对比区段Fig.6 Parameter comparison section

使用模拟退火粒子群算法从小冲杆试验载荷-位移曲线中提取材料J-C 本构模型参数的流程如图7所示。首先随机预设一组材料的塑性参数Q、B、n，将其输入有限元软件中模拟小冲杆试验，获得对应的载荷-位移曲线；然后将获得的曲线与小冲杆试验弹塑性参数对比段进行对比，计算二者之间的偏差，其偏差可视为预设材料参数的函数，表示为：

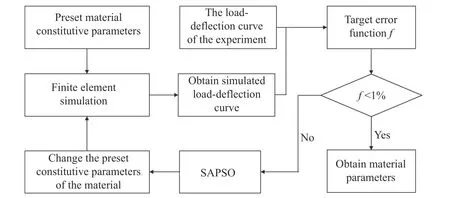
图7 有限元反演方法获取材料参数流程图Fig.7 Procedure of obtaining material parameters by inverse method

其中：f(Q,B,n) 表示试验曲线和模拟曲线的误差，N为数据点个数，Fj,FE、Fj,Exp分别表示相同加载深度下的模拟载荷与试验载荷。

获取两条曲线误差之后，判断是否满足要求（设为1%），若满足要求，则计算终止，预设参数即为材料塑性参数；若不满足要求，则通过智能算法改变输入参数，进行新一轮的对比计算，直至误差低于1%。获取材料塑性参数后，将其作为已知条件，代入有限元模拟，以小冲杆试验曲线的损伤参数对比段为目标，迭代计算损伤参数，其具体计算流程与塑性参数组类似。

2.3 小冲杆试验有限元模型的建立

本研究采用的有限元软件为ABAQUS。由于小冲杆试验的模型及边界条件均具有轴对称的性质，因此将其简化为二维轴对称模型。陶瓷珠及上、下夹具设置为刚体，试样为变形体，泊松比为0.3，弹性模量设为200 GPa。上、下夹具、陶瓷珠与试样间设置接触，摩擦因数采用0.2。单元选择四节点轴对称缩减积分单元（CAX4R），网格尺寸为0.05 mm×0.05 mm。图8 为小冲杆试验的有限元模型示意图。

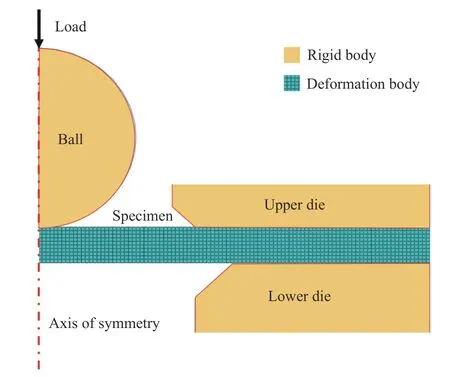
图8 小冲杆试验有限元模型示意图Fig.8 Schematic diagram of small punch test finite element model

2.4 模拟小冲杆曲线的计算结果

X65 管线钢经过多轮计算，弹塑性对比段最小误差为1.24%，损伤对比段误差为0.80%；X70 管线钢经过多轮计算，弹塑性对比段误差为0.99%，损伤对比段误差为0.44%。两种管线钢对比提取的J-C 本构模型参数如表2 所示，其参数所对应的模拟曲线如图9 所示。从图中可以看出，模拟曲线与试验曲线已相当接近。在曲线末端，模拟曲线比试验曲线略微上翘，原因可能是在实际试验中，试样由于并非完全均匀，裂纹一般在最薄弱处起裂，而在有限元模拟中，其裂纹扩展仍是轴对称的[22]。

表2 材料J-C 模型参数计算结果Table 2 Parameter calculation results of J-C model for materials

图9 模拟曲线与试验曲线的比较Fig.9 Comparison between simulation curve and test curve

3 单轴拉伸试验有限元模拟

为了将提取的J-C 本构模型参数用于模拟单轴拉伸试验，从而获取材料的断后伸长率和断面收缩率，建立了如图10 所示的有限元模型。模型及边界条件均具有轴对称特性，因此将其简化为二维1/2 平面模型，单元类型选用轴对称单元（CAX4R）。模型尺寸与实际拉伸试样尺寸相同。夹持端施加10 mm位移约束，平行段最右侧施加x轴对称约束。为了提高计算速度和精度，利用过渡网格对平行断裂段进行网格加密，细化前最大网格尺寸为0.3 mm×0.3 mm，由于J-C 本构模型参数与网格尺寸相关，因此细化后网格尺寸仍为0.05 mm×0.05 mm。

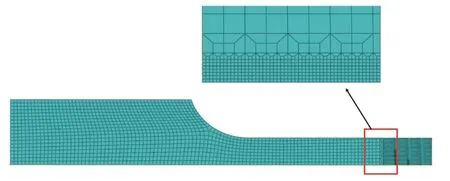
图10 单轴拉伸试验有限元模型Fig.10 Finite element model of uniaxial tensile test

模拟得到塑性性能指标的计算参数如图11 所示，图中Lu为断后标距，Ru为断后截面半径。

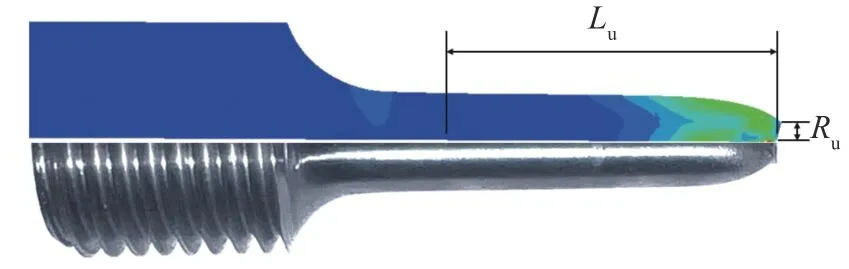
图11 塑性指标的计算Fig.11 Calculation of plasticity index

断后伸长率（A）和断面收缩率（Z）的计算公式见式（10）和式（11）。

式中：L0是原始标距，S0为平行段原始横截面积，Su为断后试样的最小横截面积。

表3 所示为小冲杆试验与单轴拉伸试验测得的材料塑性结果对比。从表3 中的数据可以看出，通过以上方法，从小冲杆试验的载荷-位移曲线获得的材料塑性参数中，仅X65 管线钢的断后伸长率与试验结果相差较大，相对误差为23.58%，但其绝对误差仅为4.48%；X65 管线钢的断面收缩率及X70 管线钢的断后伸长率、断面收缩率均与试验结果较为接近，误差均在10%以内，X65 管线钢的断面收缩率、X70 管线钢的断后伸长率和断面收缩率的绝对误差分别为3.07%、1.91%和1.41%。

表3 小冲杆试验和单轴拉伸试验测得的材料塑性指标结果对比Table 3 Comparison of the results of material plasticity index measured by small punch test and uniaxial tensile test

采用此种方法获得的X65 管线钢断后伸长率误差偏大的原因是：在基于模拟退火粒子群算法，对小冲杆试验曲线进行迭代逼近时，模拟的X65 管线钢小冲杆曲线的弹塑性对比段与实际曲线的相对误差为1.24%，未能如同X70 管线钢一样收敛至1%以下，且损伤对比段曲线误差也大于X70 管线钢。这是由于J-C 本构模型作为一个用于金属大变形、高应变率和高温情况的理想刚塑性强化模型[23-24]，实际钢材的应力-应变关系与理想模型存在一定的差异。最终导致所获取的J-C 本构参数及塑性参数仍与实际值存在一定误差。从X70 管线钢的数据也可以看出，通过智能算法，误差函数收敛值越小，最终获得的J-C 本构模型参数及模拟获得的塑性参数结果将越接近实际值。除此之外，X65 管线钢实际断后伸长率为19%，模拟获得的断后伸长率与实际值的绝对误差值小于5%，但由于本身对比值较小，因此相对误差比较大。

在有限元模拟小冲杆试验以及单轴拉伸试验的过程中，本文采用了Johnson-Cook 模型来描述材料的本构关系，且假设单轴拉伸试验以及小冲杆试验的真应力-应变曲线一致，即描述小冲杆试样变形的真应力-应变曲线也能用于描述单轴拉伸试样的变形。这两种假设均广泛应用于小冲杆试验的研究[25-29]，因此认为本文建立的从小冲杆试验评价材料塑性性能的方法具有普适性。

因此，借助模拟退火粒子群算法，从小冲杆试验的载荷-位移曲线中，通过有限元反演方法可以较为准确地获取材料J-C 模型本构参数，并可用于有限元模拟，从而准确高效地评价金属材料的塑性性能。

4 结 论

由于小冲杆试验存在尺寸效应以及几何非线性的问题，从小冲杆试验获取材料的断后伸长率和断面收缩率一直是一个难题，以往的少数研究均采用经验关联的方法，适用范围有限。本文借助了有限元模拟和模拟退火粒子群算法，实现了从小冲杆曲线中提取材料J-C 本构参数，并通过模拟单轴拉伸试验获得材料的断后伸长率和断面收缩率，从而建立了小冲杆试验评价材料塑性性能的方法。该方法基于被广泛采用的单轴拉伸试验与小冲杆试验真应力应变曲线一致假设，因此具有普适性。

通过这个方法获得的X65 管线钢的断后伸长率的绝对误差为4.48%，由于比对值相对较小，其相对误差为23.58%，断面收缩率绝对误差为3.07%，相对误差为3.70%；X70 管线钢的断后伸长率绝对误差为1.91%，相对误差为8.20%，断面收缩率的绝对误差为1.41%，相对误差为1.72%。说明通过该方法从小冲杆试验曲线中获取的材料塑性参数具有一定的工程参考价值，为评价材料塑性性能提供了另一种可靠途径。