基于RF-RFE算法的地铁车站洪涝灾害预测研究
白 莲,刘 平
(兰州理工大学土木工程学院,兰州 730050)
1 研究背景
洪涝灾害一直是威胁人类社会发展的重要因素之一。近年来,中国城市化进程快速发展,但城市防洪防灾基础配套设施与城市化快速进程需求未能匹配,我国每年遭受洪涝灾害的城市超过百座,其中发生地铁车站洪涝灾害的案例更是屡见不鲜。同时,由于地铁车站的建筑结构和运行环境均处于封闭或者半封闭状态之中,因此,一旦发生地铁车站洪涝灾害,车站内的相关设备设施出现故障,地铁运行系统受阻,且救援难度也较大,严重威胁了人员的生命安全,并造成大量的经济损失。
目前,国内外学者对地铁车站洪涝灾害进行了大量研究。在灾害防汛措施方面,AOKI等[1]依据地铁车站系统的防汛措施,开发了能够承受15m深洪水压力的滑动门;LIN等[2]基于流体容积模型方法,模拟了挡洪设施失效后,洪水入侵地铁车站的全过程,为极端天气下地铁车站的安全设计提供了参考;LIU等[3]将改进的投影寻踪模型(PPM)运用到地铁车站工程抗涝能力评价中,有效地处理了地铁车站工程抗涝能力的高位数据;赵露薇等[4]研究了暴雨干扰下地铁系统脆弱性形成机制,以期为暴雨天气下地铁系统安全运营提供参考建议。在灾害应急管理方面,马晴晴等[5]将降雨情景下的地表积水分布与地铁站进行耦合,量化了积水对地铁站的干扰程度,为地铁站制定应急管理措施提供了新思路;WU等[6]为地铁车站工程暴雨内涝灾害应急预案,提出了一种基于语言直觉模糊集、结构熵权和TOPSIS的群决策方法;LONG和ZHANG[7]提出了一种改进经验公式的应急疏散引导方案,研究行人行为对引导疏散的影响,通过地铁车站疏散模拟实验,提供了相应的应急疏散措施。在灾害风险评估方面,闫绪娴等[8]构建了韧性城市下地铁洪涝灾害风险分析模型,从韧性角度对地铁系统洪涝灾害防治提出针对性建议;LYU等[9]对地铁系统的洪水风险进行了评估研究,以期增加地铁系统功能恢复力;YU等[10]采用组合赋权法,建立了地铁车站内涝风险的模糊综合评价模型,为地铁车站内涝风险评估提供了新思路。
然而,上述研究均集中在灾害管理及风险评估方面,缺少对地铁车站洪涝灾害的预测研究,若能在极端天气情况来临前,依据相关变量建模预测某地铁车站是否会发生洪涝灾害,可帮助车站相关管理人员制定合适的应对措施,加强地铁车站防洪减灾的能力。因此,李辉山、白莲等[11]提出了一种基于DNN神经网络的地铁洪涝灾害预测方法,并取得了较好的预测效果,但该方法在变量选择时未降低相关数据维度及未去除变量间的冗余,在进行预测时,数据的复杂度和冗余信息会严重影响到整个预测过程的速度以及整体的数据检测性能。随机森林-递归特征消除(random forest-recursive feature elimination,RF-RFE)方法能够处理大量数据和评价正则化回归特征变量的重要性,该方法在去除冗余特征的同时,可筛选出最佳特征变量,有效地缩短数据训练和交叉验证的时间,提高预测模型的运算速度及数据检测性能。
综上,基于RF-RFE和DNN神经网络,提出了地铁车站洪涝灾害的预测方法。首先,使用发生地铁车站洪涝灾害的实测数据,构建灾害初始变量集,通过随机森林-递归特征消除(random forest-recursive feature elimination,RF-RFE)方法选出重要变量;其次,使用重要变量数据训练DNN神经网络,得到最优网络结构;最后,将实测灾害数据输入预测模型,测试分析预测模型性能。该方法优化了灾害变量集,降低了敏感数据对模型预测结果的影响,提高了预测模型的准确率,实现了对地铁车站洪涝灾害的准确预测。
2 变量集构建
2.1 初始变量集选择
通过灾害实际案例、文献查阅和专家访谈的形式,初步确定地铁车站洪涝灾害变量集。为保证文献查阅的完整性、代表性和科学性,在SCI-E、Elsevier、中国知网、万方等数据库输入“地铁车站内涝”“地铁车站灾害”“城市轨道交通暴雨”等关键词,检索出相关文献。依据全面性文献筛选原则,梳理出17个灾害变量集,将17个灾害变量集发送给具有相关理论基础的专家,通过“专家意见—反馈说明—修改意见—统一意见”程序,多次循环往复,最终确定13个地铁车站洪涝灾害变量集。所确定的灾害变量集如表1所示。

表1 地铁车站洪涝灾害变量集
由表1可知,地铁车站洪涝灾害的原因主要表现在以下3个方面。(1)气候变暖和城市化效应。据相关研究指出[12],未来极端气候出现的概率会大大增加,随着我国城市化进程的快速发展,大量基础设施和城市更新等建设项目改变了原有城市构造[13],使得城市路面硬化严重、城市周边部分河道被填埋及城市调蓄能力下降等,如若遇到极端强降水天气,极易发生城市内涝,引发地铁车站洪涝灾害事故。(2)地铁车站排水系统能力[14]。车站排水系统主要依附市政排水系统,强降雨导致市政排水系统超负荷运作,造成排水管道爆裂或堵塞,使得车站周边积水过多,易发生积水倒灌现象。(3)应急管理措施[15]。地铁车站应急管理措施能及时降低发生洪涝灾害的风险、减少人员伤亡和财产损失,最快恢复车站运营秩序。
2.2 基于RF-RFE的变量选择
采用RF-RFE算法从地铁车站洪涝灾害初始变量中选择重要变量,能够随机选取样本和特征,还可使模型有较好的拟合和抗噪能力,提高分类的正确率[16]。
2.2.1 随机森林和变量重要性分析
随机森林(Random Forest,RF)是一种多棵决策树集成学习算法[17],其思想是运用统计学理论,利用Bootstrap重抽样方法从原始训练样本中得到多个训练子集,并对每个子集进行决策树建模,多棵决策树集合构建为随机森林,所有决策树预测平均值为最终预测结果,算法的主要步骤如下。
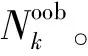
(2)从所有样本中随机选择x个变量,n个训练子集与x个变量构建一棵决策树,在决策树的每个节点处抽取mtry个变量,计算每个变量蕴含的信息量,并选择分类能力最佳的变量进行节点分裂。
(3)重复前面步骤,直至生成含有m棵决策树的随机森林。
(6)变量φx的重要度计算如式(1)所示。
(1)
2.2.2 RF-RFE算法
递归特征消除(Recursive Feature Elimination,RFE)是反复构建模型,直至选出最优特征子集的一种特征变量排序选择方法[18]。RF-RFE算法是将RFE方法引入随机森林算法,并对变量重要性排序进行选择。本文选择RF-RFE算法是考虑到该算法有助于减少冗余信息对算法的影响,可提高地铁车站洪涝灾害变量分类正确率。RF-RFE算法步骤是通过“训练初始变量集—计算变量重要性—变量重要性排序—删除重要性最小变量—计算分类正确率”递归重复过程,直至所有变量计算完毕,将分类正确率最高的训练集所对应的变量作为重要变量,具体流程如图1所示。
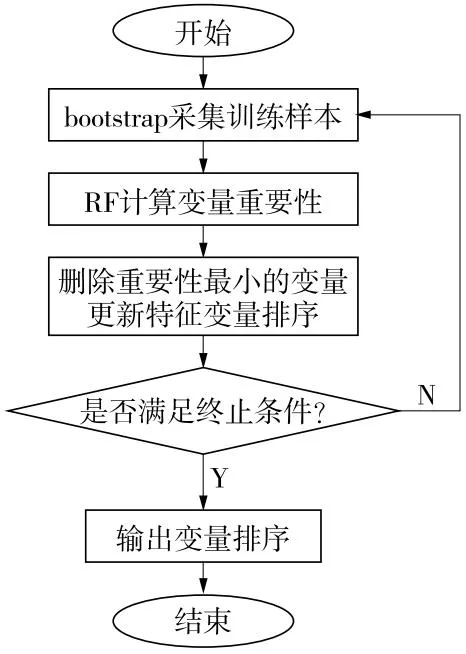
图1 RF-RFE算法流程
3 基于RF-RFE和DNN神经网络的预测模型
3.1 DNN神经网络基本原理
DNN(深度神经网络,Deep Neural Networks)是一种深层学习,在1986年由D.E.Rumelhart和J.L.McCelland等在研究BP神经过程中被提出。DNN神经网络主要具有以下优势:(1)强大的非线性拟合能力;(2)强特征提取能力;(3)较强的刻画能力。基于以上优点,选择DNN神经网络构建地铁车站洪涝灾害预测模型,可规避非线性灾害数据的过度拟合,使得模型具有良好的表达能力。
DNN深层神经网络由3个部分组成:DNN的拓扑结构、激活函数与损失函数、训练DNN算法[19]。DNN神经网络结构如图2所示。

图2 DNN神经网络结构
在图2所示网络结构中,x1,x2,…,xn为DNN神经网络输入值;b为隐含层神经单元的偏置值;w1,w2,…,wn为神经单元连接的权值;y为神经元输出,可按照式(2)计算,其中g为神经元激活函数,本文使用tanh、Sigmoid激活函数,分别如式(3)、式(4)所示。
y=g(z)=g(wx+b)
(2)
(3)
(4)
3.2 RF-RFE和DNN神经网络算法流程
RF-RFE和DNN神经网络算法包括以下两个部分:①利用RF-RFE算法得到地铁车站洪涝灾害重要变量;②以重要变量为输入样本,训练DNN神经网络预测模型。算法流程如图3所示,具体步骤如下。
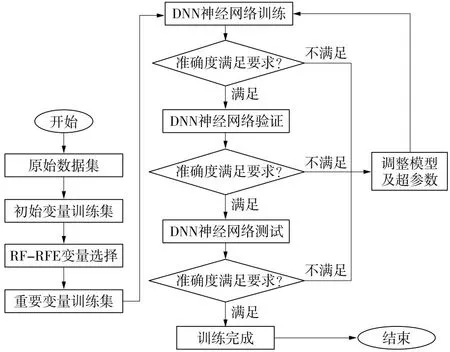
图3 RF-RFE和 DNN神经网络算法流程
(1)收集地铁车站洪涝灾害数据。
(2)使用RF-RFE算法计算分类样本的正确率,得到重要变量。
(a)初始变量训练集输入为
训练集的输出为
式中,n为训练样本总数;xi,j为第j个输入样本的第i个变量;第i个变量的具体内容见表1;yj∈{0,1}为第j个输入样本所对应地铁车站洪涝灾害事件的判别标签,0表示未发生地铁车站洪涝灾害,1表示发生地铁车站洪涝灾害。
(b)使用RF训练13个初始变量集,计算变量重要性并记录分类正确率。
(c)删除重要度最小的变量,重新训练变量集,计算变量重要性并记录分类正确率。
(d)重复步骤(c),直至所有变量集训练完毕,最高分类正确率的训练集所对应的变量为重要变量。
经过步骤(2),可得13个初始变量的重要性排序以及每个训练集的分类正确率,最高分类正确率的训练集所对应的输入变量为重要变量。
(3)构建重要变量训练集,训练DNN神经网络。
使用重要变量构建训练集来训练DNN神经网络,本网络选取精准率P、召回率R、F1分数(调和平均数)、准确率(Accuracy)等4个指标作为模型评价指标。TP代表预测正确的发生地铁车站洪涝灾害数量;TN代表预测正确的未发生地铁车站洪涝灾害数量;FP代表未发生地铁车站洪涝灾害中错误预测为发生地铁车站洪涝灾害数量;FN代表发生地铁车站洪涝灾害中错误预测为未发生地铁车站洪涝灾害数量;F1是P和R的调和平均数,F1越接近为1,说明模型表现越好,计算如式(5)~式(8)所示。
(5)
(6)
(7)
(8)
4 实例分析
4.1 样本数据及预处理
本文样本数据来源于发生地铁车站洪涝灾害的案例,共248组数据,其中正样本为遭受地铁车站洪涝灾害共129组数据,负样本为未遭受洪涝灾害共119组,正负样本比例约为0.52∶0.48。样本数据信息主要依靠国家气象信息中心、百度地形图、城市轨道交通工程项目建设标准和防洪标准等官方发布信息与国家规范[20-22],其中部分数据依靠新闻发布的实时信息来源于https://www.chinanews.com.cn/china/,数据处理为优良中差4个等级,对应数值4,3,2,1,发生地铁车站洪涝灾害为1,未发生地铁车站洪涝灾害为0。
为提升训练速度和分类效果,消除样本之间量级不同所造成的影响,将所有数据使用最值归一化处理且映射到[0,1],归一化计算如式(9)所示。
(9)
式中,xscale为归一化后的数据;x为原始数据;xmax、xmin为原始数据的最大、最小值。
4.2 变量选择
使用RF-RFE算法对地铁车站洪涝灾害的变量进行筛选并评价时,需要人工对随机特征变量个数及决策树数量等重要参数进行设定。随机特征变量个数为特征变量总数的平方根,此处设置为4,决策数的数量设置为50。经过RF-RFE算法提取后,地铁车站洪涝灾害初始变量的重要性排序为:{C1,C7,C6,C9,C4,C10,C12,C11,C5,C3,C8,C2,C13}。每删除重要性排序在最后一位变量时,需重新训练变量集并计算分类正确率。分类正确率随变量个数的变化曲线如图4所示。
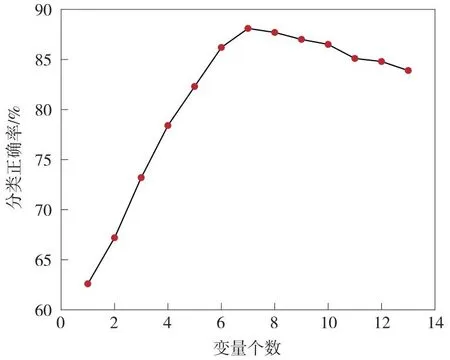
图4 分类正确率与变量个数关系曲线
如图4所示,当变量个数少于7时,分类正确率整体呈上升趋势;当变量个数等于7时,分类正确率达到峰值为88.1%;当变量个数大于7时,分类正确率呈下降趋势;在所有变量都被计算时,分类正确率为83.74%,与选用重要性排序前7个变量数相比,分类正确率下降了4.36%。因此,本研究选择重要性排序靠前的7个变量(C1降雨量、C7积水回灌、C6河道影响、C9防洪高程设计、C4地区年降雨量、C10排水系统能力、C12信息调度能力)作为地铁车站洪涝灾害预测的重要变量,部分重要变量训练集如表2所示,行向量表示训练样本,列向量表示重要变量,训练集输入矩阵如式(10)所示。
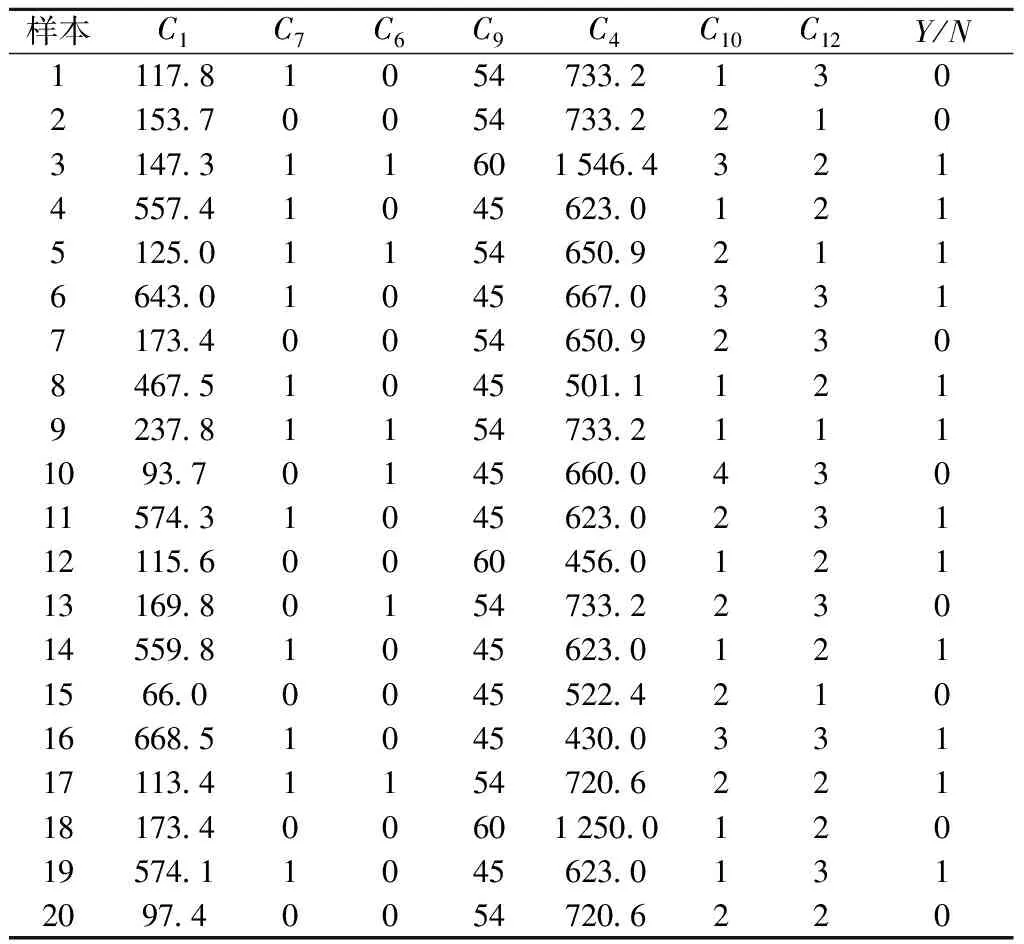
表2 重要变量训练集节选
input=
(10)
4.3 DNN神经网络模型
DNN神经网络主要包含隐藏层的层数和各隐藏层的节点数目两部分,本研究利用重要变量构建的训练集训练DNN神经网络。具体网络结构为1层输入层、6层隐含层和1层输出层,其中,输入层神经元节点为重要变量;隐藏层神经元激活函数选用tanh函数、dropout(随机失活)=0.1、r(学习率)=0.000 5;输出层为1个神经元节点,即是否发生地铁车站洪涝灾害,激活函数Sigmoid将数据映射到[0,1]中,取阈值为0.5,即输出层输出大于0.5时预测为发生地铁车站洪涝灾害,小于0.5时预测为未发生地铁车站洪涝灾害。该网络选用二分类交叉熵损失作为损失函数,如式11所示。
(11)

4.4 训练结果与分析
通过准确率和F1分数两个评价指标来衡量DNN预测模型,预测模型训练集、验证集和测试集的准确率变化如图5所示。
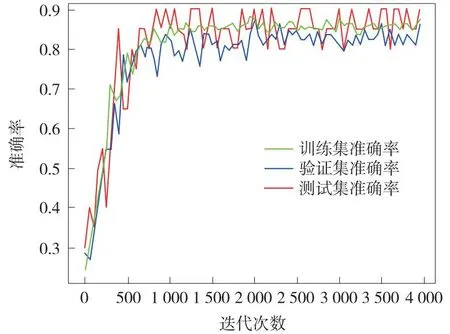
图5 DNN模型准确率预测结果
如图5所示,3种样本的准确率随着训练进程而显著提升,前1 000次迭代中训练集、验证集和测试集的准确率快速上升;中间1 000~2 500次迭代中,训练集的准确率稳定在0.86~0.88之间,验证集的准确率在0.84处上下波动,测试集的准确率在0.80~0.9之间波动;后2 500~4 000次迭代中,训练集的准确率在0.87处保持平稳,验证集的准确率波动范围缩小,在0.85处保持相对平稳,测试集的准确率达到0.85~0.9。这表明了该模型具有良好的预测精度和模型泛化能力。
图6为DNN神经网络训练集、验证集和测试集的F1分数变化图,前1 000次迭代快速上升,后1 000~4 000次迭代中,训练集、验证集和测试集F1分数值稳定在0.87~0.90之间,说明模型未过度拟合且表现良好。

图6 DNN模型调和平均数曲线
5 结论
通过地铁车站洪涝灾害实例研究、文献查阅及专家访谈方法,筛选出影响发生地铁车站洪涝灾害因素作为初始变量集;并采用随机森林—递归特征消除(RF-RFE)算法进行初始变量集优选,构建了重要变量集;最后,将重要变量集作为DNN神经网络模型的输入变量,对DNN神经网络进行了训练,得到地铁车站洪涝灾害预测模型。主要结论如下。
(1)RF-RFE与DNN神经网络算法结合,与未去除变量信息冗余相比,有效降低了DNN神经网络算法的输入维度,提高了预测模型的运算速度。以重要变量为输入的DNN神经网络模型更具有良好的性能,准确率提升了4.36%,验证了选择重要变量可以提高DNN神经网络算法的预测精度,证明RF-RFE和DNN神经网络算法相结合的预测方法具有理论意义。
(2) 基于RF-RFE与DNN神经网络预测模型在地铁车站洪涝灾害案例中的预测准确率结果为88.1%,F1分数为90%,说明预测模型具有较好的识别能力和泛化能力,能够满足对于地铁车站洪涝灾害预测的需求,证明该预测方法具有应用价值。
为得到更具有普遍性的结论,后续研究需要将RF-RFE与DNN神经网络算法用于其他数据库,并从理论上分析和论证该方法应用于数据处理的优越性。此外,可继续补充和提炼灾害数据样本,如何构建更全面的地铁车站洪涝灾害初始变量集有待进一步讨论。

