高铁桥梁装配式双柱空心墩承插深度研究
袁得铮,邵长江,2,韦 旺,漆启明,崔皓蒙
(1.西南交通大学土木工程学院,成都 610031; 2.西南交通大学陆地交通地质灾害防治技术国家工程研究中心,成都 610031)
引言
预制桥墩体系有着施工速度快、环境影响较小、降低造价的优势,已得到广泛应用[1]。承插式施工是一种将预制桥墩垂直插入承台预留槽口,通过间隙灌浆形成整体,具有拼装工序简单、施工精度要求相对较低、现场工作量小等优点。与灌浆套筒[2]、灌浆金属波纹管等装配连接措施相比,进一步加快了施工速度,优势显著,因而得到了广泛研究。但其在铁路桥梁上抗震性能研究尚处于起步阶段,适用于高烈度地区的承插深度还有待研究。Osanai和Canha等[3-5]较早开展了建筑结构的柱-基础承插式连接试验研究,为满足抗震要求,承插深度不小于0.5D(D为墩柱外径)。但因桥梁结构中的预制墩柱截面尺寸、承受荷载量级等与房屋建筑结构墩柱相差较大,上述连接构造能否直接用于桥梁工程尚需进行深入研究。
预制墩柱与承台之间的合理连接有助于改善墩身抗震性能,Pul等[6]设计了6种不同承插式连接方式;杨先凡等[7]总结了预制拼装桥墩不同连接形式,分析了不同连接方式的优缺点;陈金彪等[8]提出了确保连接质量的施工工艺。承插式桥墩连接方式、承台厚度受承台配筋、混凝土强度和承插深度及其细部构造等因素的影响,而承台厚度又取决于承插深度。
承插深度是承插式桥墩的关键参数,大量研究表明,采用1.0D及以上承插深度的桥墩性能与现浇墩几乎等同,甚至更好。Motaref[9]和Kavianipour等[10]用高强水泥作为承插部位的灌浆料,发现承插深度为1.5D时,可以确保桥墩与承台之间的整体性;Han等[11]通过试验研究发现在1.5D时,承插式桥墩的承载力、延性和耗能均大于现浇墩;Mohebbi等[12]进行大比例尺单柱墩和双柱墩的振动台试验,发现承插深度为1.36D时,墩与承台连接可靠;李永波等[13]通过拟静力试验表明,1.1D承插深度下承插式桥墩抗震性能接近或略高于现浇式桥墩;Mashal等[14]进行新西兰一座公路桥梁的拟静力试验,发现承插式深度为1.0D时,装配式墩与整浇墩性能相似;Haraldsson等[15]开展不同承插深度和预应力,Khaleghi等[16]开展排架墩柱的试验研究,得到了与Mashal相同的结论。
大量研究表明:承插深度在1.0D时可以达到与现浇墩的等强设计[17],为了减小承台厚度,加强环境保护,需要考虑承插深度小于1.0D的情况是否满足等强设计的要求。Jin等[18]进行拟静力试验研究,发现0.7D承插深度桥墩和现浇墩具有同样好的抗震能力;杨先凡等[7]对0.7D及以上承插墩柱和现浇墩进行数值模拟研究,所得发现与Jin等[18]相同;徐艳等[19]关于公路现浇墩柱和4个不同承插深度预制墩柱的拟静力试验,发现采用0.5D承插深度预制墩柱的抗震性能与整体现浇墩基本一致。大量学者的研究成果表明,0.5D的承插深度可以满足公路及市政桥梁的抗震性能要求。
为保证高速列车安全运行和旅客乘坐的舒适度,高铁桥墩一般采用更大的尺寸,使其上下部结构与公路市政桥梁有显著差别,现有公路桥梁和市政桥墩承插深度的研究是否适用于高铁桥墩有待深入研究。同时承插式高铁桥墩抗震性能研究较公路少,尤其是对于高烈度地区的高铁双柱墩的研究更为缺乏,双柱墩相较于独柱墩具有明显的框架效应、横向刚度更大及稳定性更强的特点。现有承插深度是否适用于高烈度地区的高铁双柱墩还需进一步研究。
本文依托某高速铁路双柱式桥墩工程项目,基于OpenSees模拟平台,采用纤维截面进行建模,考虑柱高及桥墩外径对承插深度的影响,对比分析承插式桥墩和现浇桥墩的异同。在进行拟静力试验分析的基础上,基于承插段钢筋应变变化和纵筋强度发展长度提出了最小理论承插深度的计算公式,为承插式桥墩抗震设计提供参数依据。
1 高速铁路桥梁承插式空心墩概况
1.1 桥墩结构及构造
双柱桥墩结构构造如图1所示,包含承台、插入承台节段、预制墩身、盖梁及灌浆料。承插部分使用C40微膨胀混凝土进行灌浆,微膨胀混凝土具有更好的黏结效果,能够加强墩柱底面与承台的连接。为探明双柱空心墩墩高和桥墩外径对承插深度的影响,分析了5,10 m两种墩高分别采用内径1.5 m、外径2.4 m及内径1.1 m、外径2 m的情况,承插深度也从0.5D逐渐加到1.0D。承插式桥墩的参数如表1所示。为对比承插式双柱墩与现浇双柱墩在往复位移下的抗震性能差异,另外又增加了4个现浇墩,具体参数如表2所示。

表1 高铁承插式双柱墩参数

表2 高铁现浇双柱墩参数
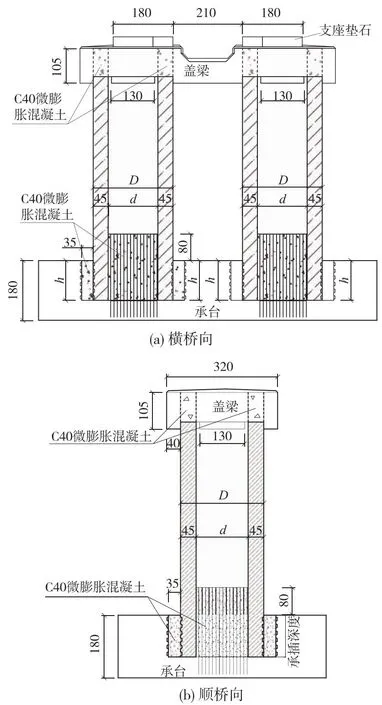
图1 高铁现浇双柱桥墩结构模型构造(单位:cm)
模型外缘环向纵筋皆采用φ20 mm的HRB500高强钢筋,净保护层厚度为35 mm;内缘环向纵筋皆采用φ16 mm的HRB500高强钢筋,净保护层厚度为37 mm。内外缘均布置φ16 mm的HRB400箍筋,竖向间距为110 mm。纤维截面中的核心区混凝土强度用Mander约束本构确定,非约束混凝土强度按照材料的标准值确定。
1.2 有限元模型
采用OpenSees软件建立桥墩有限元模型。灌浆料采用只受压不受拉的ENT(elastic-no tension)材料,该材料的弹性模量根据混凝土弹性模量取值。预制墩柱和盖梁通过非线性梁柱单元模拟,墩柱截面使用纤维截面。盖梁与墩柱处力学特性准确模拟对于预制拼装桥墩来讲是非常重要的,往复荷载下接缝处可能会开口或者出现横向错位。因此,要选用合适的材料和单元来模拟接缝的力学性质。本文采用不考虑混凝土受拉的Concrete01模型模拟接缝处混凝土,由于接缝处受箍筋约束较弱,因此采用素混凝土进行模拟,穿过接缝截面伸入到盖梁里的纵筋通过纤维截面进行考虑,且该桥墩由于盖梁下面设有凸台,如图2所示,使得桥墩能够完全插入到盖梁中,盖梁和墩身接缝处不会产生开口且产生的错动非常小,故采用零长度纤维单元模拟盖梁与墩顶的接缝,有限元模型如图3所示。保护层及核心区混凝土均使用能够考虑受拉及加卸载刚度退化的Concrete02本构[20],钢筋则使用能够体现出滞回捏拢效应和强度退化的Steel02本构[21]。所用模型不考虑屈曲后退出工作的状态,即没有显著的承载力下降阶段。对于墩身承插段与承台之间的相互作用包括3部分:插入段水平支撑力、墩身竖向支撑力和插入段竖向摩擦力。假设承台刚度无穷大,通过多个水平弹簧模拟插入段水平抵抗力的作用,因实际墩身和底面进行了粗糙处理,不存在拔出的情况,竖向采用固结条件模拟边界。
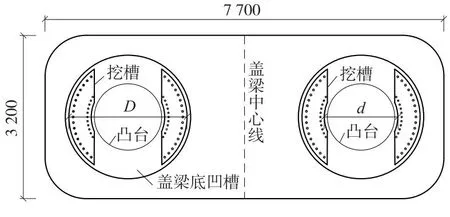
图2 高铁预制盖梁底面(单位:mm)
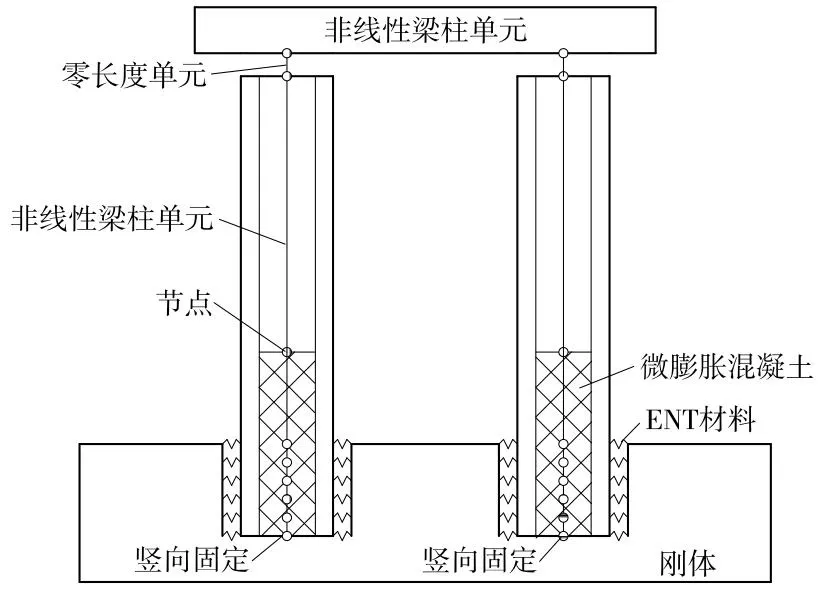
图3 高铁桥墩有限元模型
1.3 加载方案设计
根据设计方案,上部结构恒载产生的轴向压力为14 000 kN,施加横向循环位移荷载时,由于有限元模拟没有考虑多次循环位移下的累计损伤且多数试验得到循环位移下的滞回环相差很小,故每级峰值位移只加1次。根据《Caltrans seismic design criteria》[22]规范的规定,φ32 mm及以下钢筋的偏小极限受拉应变为0.09,墩柱底部钢筋最大应变不超过该值。加载偏移率分别选择为0.1%、0.2%、0.3%、0.4%、0.6%、0.8%、1.0%、1.2%、1.4%和1.6%。
2 模拟方法的试验验证
铁路桥墩和公路桥墩总体构造基本相同,所以建模方法差别不大,且文献中能查到的铁路桥墩试验数据较少,故选用坎特伯雷大学Mashal等[14]2014年的承插式双柱预制拼装桥墩拟静力试验来验证模拟方法的正确性。桥墩属于新西兰一座典型的跨度为16 m的公路桥梁,桥墩采用圆形实心截面,试验模型的直径为500 mm,柱高为2 615 mm,承插深度为500 mm。在墩身下部的500 mm高度,纵筋配筋率为0.98%,箍筋配置率为1.00%;墩身上部的2 115 mm高度,纵筋配筋率0.82%,箍筋配置率为0.50%。试验采用的混凝土标准抗压强度为40 MPa,两个墩柱的设计参数相同,拟静力试验采用位移加载。详细的试验参数和结果参考文献[14]。预制双柱墩模型如图4所示。

图4 高铁预制双柱墩示意(单位:mm)
由于预制墩身时墩顶预留了纵筋,盖梁中预留了孔道,接缝截面采用零长度单元模拟。模型中盖梁、主墩身和插入段的墩身均采用基于柔度法的非线性梁柱单元模拟,下部承插位置采用多弹簧来考虑,且采用的位移加载模式与试验的位移加载完全一样。具体建模方法及本构关系与上述有限元模型相同。
模拟结果如图5所示,可以发现滞回曲线与Mashal等[14]通过试验所得整体吻合较好,表现出明显的捏缩效应,滞回曲线较为饱满,塑性变形能力强,正负向水平承载力峰值分别为327.79,326.341 kN,试验结果分别为351.3,335.3 kN,相对误差为6.7%、2.6%,说明有限元模型能够较为准确地预测承插式双柱墩的滞回性能。

图5 桥墩承插式双柱墩模拟结果
3 数值模拟结果分析
3.1 滞回特性
比较现浇墩和承插式桥墩的模拟结果,如图6所示。可见混凝土构件在发生开裂前,加载曲线几乎呈线性,裂缝出现后,滞回环的面积逐渐增大,形成“旗”形,当荷载水平不断增大时,滞回环的面积逐渐趋于饱满,构件裂缝也在不断增大,由此而导致滞回曲线出现了“捏拢”现象,随着水平位移的增大,刚度退化现象越来越明显[23]。
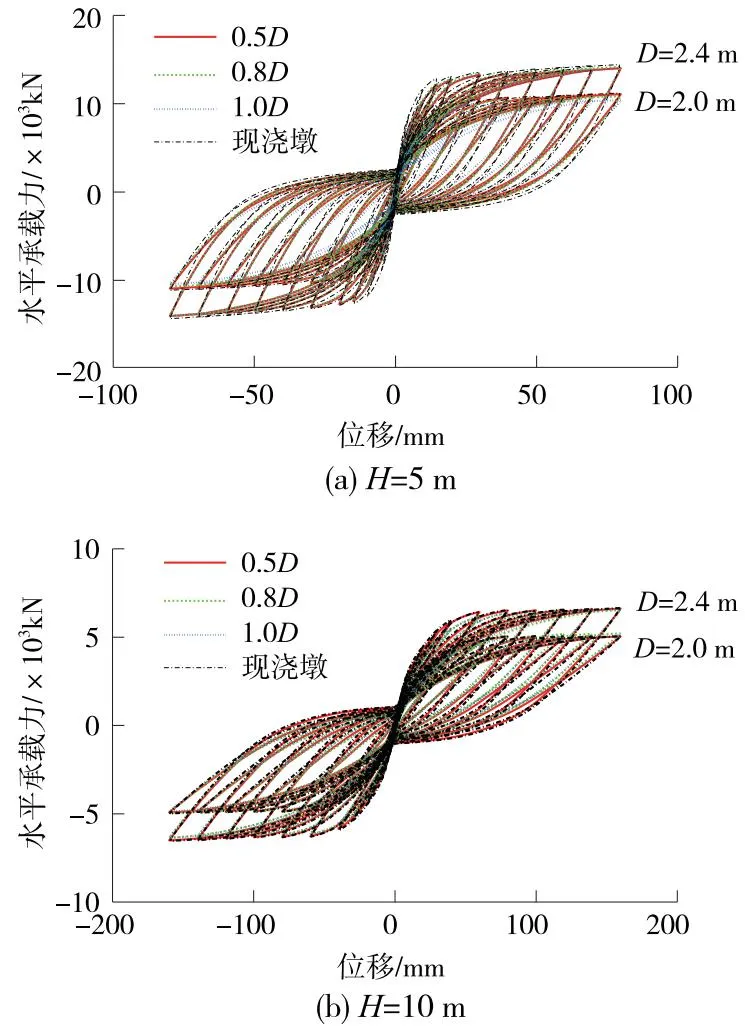
图6 现浇双柱墩数值模拟滞回曲线
现浇双柱墩和承插式双柱墩滞回曲线总体形状一样,但是现浇双柱墩的滞回曲线更加饱满,有效刚度略大于承插式双柱墩。由滞回曲线可得,承插式桥墩的残余位移小于现浇墩,这种现象是因为现浇墩和承台之间是固结的,而承插式桥墩和承台之间通过灌浆料连接在一起,灌浆料又是通过弹性单元模拟,故而承插式桥墩的残余位移较小。
由图6(a)可知,在墩高H为5 m的条件下,墩柱直径越大,承载力越高。在D=2.0 m和D=2.4 m情况下,采用0.5D、0.8D和1.0D承插深度的双柱墩和现浇双柱墩承载力几乎一样,最大相差不超过2.8%,说明当墩身外径较大时,桥墩截面直径的变化对于承插深度取值影响很小;当墩身外径达到0.5D及以上时,均可以满足桥梁的承载力需求。在墩高H=5 m条件下,不同墩柱承载力如表3所示。
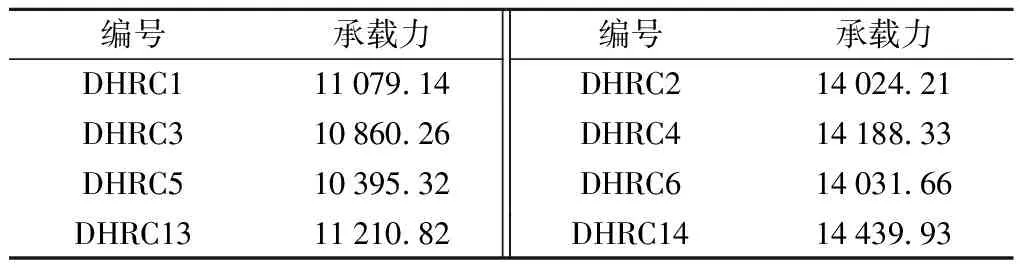
表3 墩高H=5 m墩承载力 kN
当墩高H为10 m且墩径不变时,不同承插深度墩和现浇墩的承载力相差不大,最大承载力和最小承载力相差小于1.6%。对比图6(b)可得,随着墩高增加,墩身的承载力大幅度减小。在较高的墩柱下,直径变化对于承插深度取值的影响也是很小的,在0.5D承插深度下依然有着与现浇墩相似的承载力。但墩柱较高时,最大承载力的偏差相对于矮墩柱更小,承插式墩柱承载力更接近于现浇墩。综合考虑H=5 m双柱墩和H=10 m双柱墩,高铁的墩高变化对于承插深度取值的影响是很小的,超高墩的情况需要另外研究。两种墩身高度都可以选择0.5D承插深度作为施工的安全承插深度。H=10 m墩柱的承载力如表4所示。

表4 墩高H=10 m墩承载力 kN
3.2 刚度退化
刚度退化是构件在循环荷载作用下抗震性能退化的主要因素之一,又由于构件抗震性能退化直接影响到结构抵抗地震动的能力,所以构件的刚度退化可作为评价构件抗震性能好坏的依据。
图7为各模型的割线刚度退化曲线。由于桥墩在1次循环中正负方向的损伤差别较小,所以正负方向的割线刚度基本一致。由割线刚度退化曲线可知,现浇墩和承插式桥墩刚度退化规律一致,即刚度随着侧向位移的增加而降低,位移较小时刚度退化较快,位移较大时刚度退化减慢。现浇墩的初始刚度是最大的,0.5D、0.8D和1.0D承插深度桥墩初始刚度均有所减小,在1.0D承插深度下高5.0 m、φ2.0 m墩初始刚度减小最多为21.03%;高5.0 m、φ2.4 m墩初始刚度减小最多是在0.8D承插深度下,为14.86%;高10.0 m、φ2.0 m墩在0.5D下初始刚度减小最大为11.72%;高10.0 m、φ2.4 m墩初始刚度在0.8D承插深度下减小最多为9.31%且其他承插深度减小程度也基本在此附近。说明随着墩高增加和直径加大,承插桥墩初始刚度越来越接近于现浇墩。以高10 m、φ2.4 m桥墩为例,承插式桥墩与现浇桥墩的初始刚度相差最小为5.23%,当加载到最大位移时,现浇桥墩的刚度为40.94 kN/mm,0.5D,0.8D和1.0D承插深度的桥墩刚度分别为40.71,39.80 kN/mm及39.86 kN/mm,刚度相差最大不超过3%,证明承插式桥墩即使在初始刚度上与现浇墩有所差异,但随着位移增加,刚度的差别越来越小,在达到极限位移时,刚度的差别可以忽略不计。

图7 桥墩刚度退化曲线
3.3 纵筋应变渗透
对于现浇桥墩,内部纵向钢筋在墩底至承台一定范围内,因附加转动和变形会产生渗透应变。而承插式桥墩不同,其承插段与承台并非固结,墩底曲率不一定为0,此范围内的纵筋受到应变渗透导致屈服并损伤。为量化应变渗透效应,在此给出1 000 mm承插深度内钢筋应变沿深度的变化规律,如图8所示。
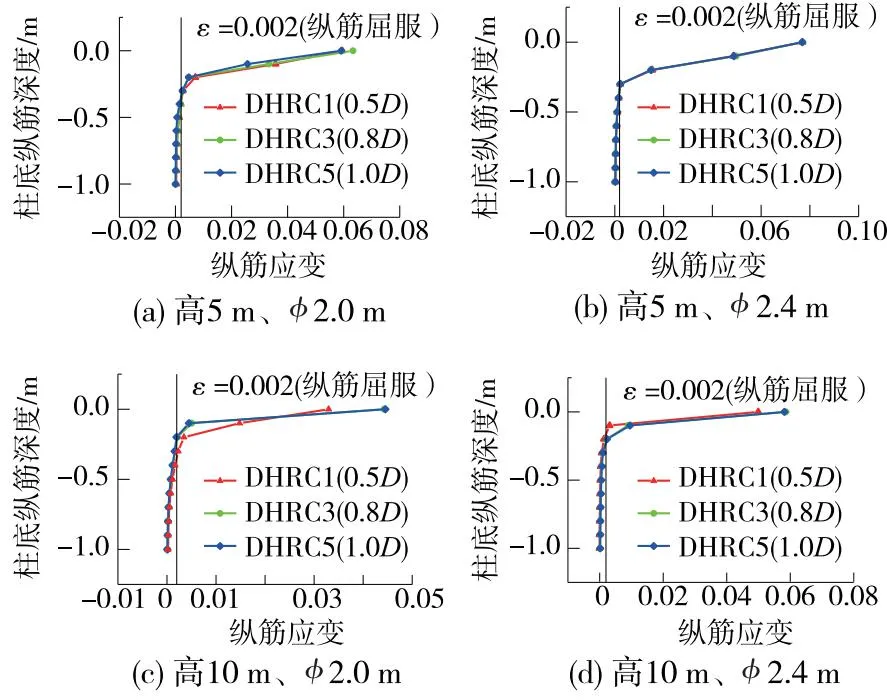
图8 桥墩纵筋应变分布曲线(位移角加载到1.6%)
由图8可知,12个承插式墩柱在承插段的应变变化趋势是一样的,承插段墩柱存在明显的钢筋应变渗透,且应变随着距离承台顶面深度的增加逐渐减小。在承台顶面以下0~400 mm范围内时,大部分钢筋屈服进入塑性,应变快速减小,应变过大容易导致承插段墩柱和承台出现开裂甚至破坏,400 mm深度以下范围内钢筋在弹性阶段,应变持续减小,有些部位拉应变甚至减小到0,可知此范围的钢筋没有完全发挥作用。由于现浇墩纵筋与承插段的纵筋传力路径不同,破坏机理差异显著,故二者纵筋应变可比性低。表5列举了12个桥墩在承台顶以下纵筋应变的变化,尽管屈服的位置不尽相同,但都是在承台顶面以下400 mm范围内达到屈服。为此,承台顶面以下400 mm为受到钢筋应变渗透影响显著区域,也是地震易损区域。
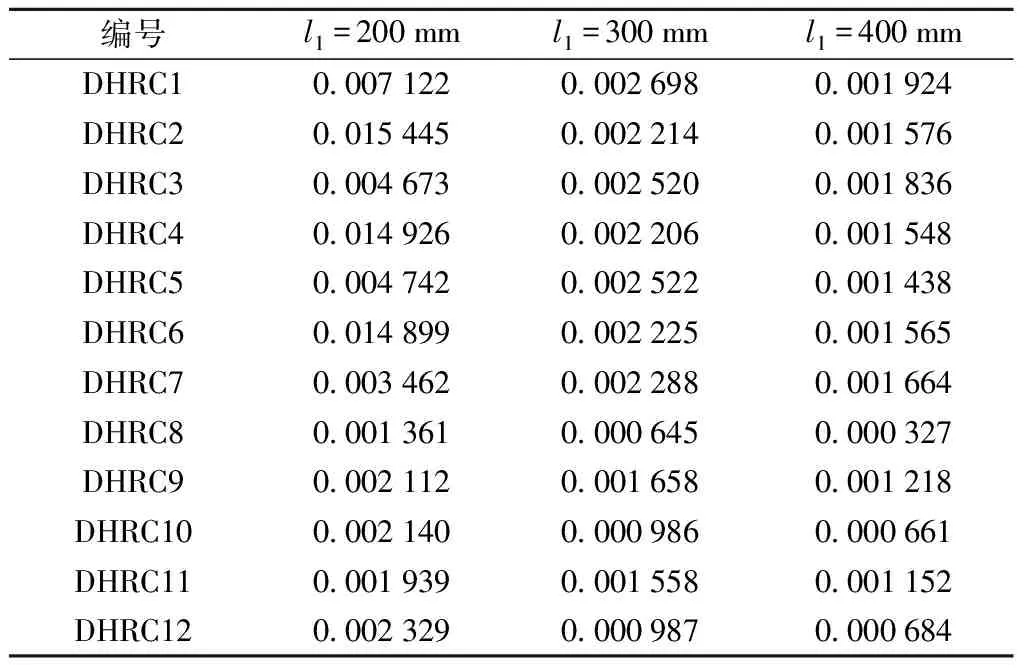
表5 承台顶下钢筋应变
3.4 最小承插深度
定义承台顶到承插段钢筋屈服时的长度为易损伤长度L1,纵筋屈服点在承台顶以下具体深度由图9所示。
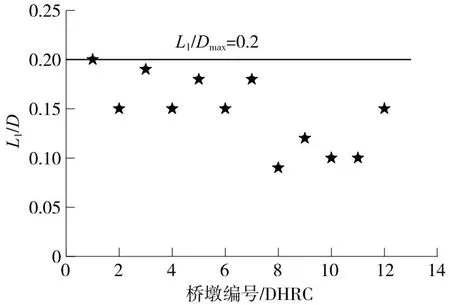
图9 纵筋屈服点具体位置分布
由图9可知,纵筋屈服点深度与墩径比值是不断变化的,可以偏于安全地取L1=0.2D。对于最小承插深度,易损伤区域的长度只是其中一部分,还应当考虑纵筋强度的发展长度(受拉直线变形钢筋的延伸长度),由纵筋屈服点处向下至其强度充分发挥的长度[24]。因此,最小承插深度可以由承台顶面到纵筋屈服处长度L1加上纵筋的发展长度L2得到,如图10所示。

图10 墩身到承插段纵筋受力及应变
通过分析可以得到承插式桥墩的最小承插深度Hmin,即
Hmin=L1+L2
(1)
L1=0.2D
(2)
L2=mablab
(3)
(4)
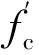
按照上述公式计算DHRC1的最小承插深度为986 mm,φ2.0 m的DHRC1桥墩的0.5D承插深度为1.0 m,略大于最小承插深度986 mm,说明该公式的合理性。
公式(1)是经过理论分析得到的,对于高烈度地震区的承插式桥墩,为保证承插式桥墩的抗震安全性,承插深度设计值应大于理论计算的最小值。该计算公式是从墩柱自身损伤的角度出发,灌浆料和承台的损伤并未考虑进去,故在实际工程中承插式桥墩的承插深度必须大于该公式计算所得的最小承插深度。
4 结论
本文采用OpenSees平台建立了高速铁路承插式双柱墩,基于Mashal等的试验结果验证了数值模型的合理性。通过大量数值模拟和分析得到以下结论。
(1)高铁承插式与现浇桥墩的承载力几乎相等,实现了等强设计,在0.5D、0.8D和1.0D承插深度下承载力变化很小,这3种承插深度均可满足实际工程。
(2)高铁现浇墩与承插式桥墩割线刚度退化规律基本一致,现浇墩的初始割线刚度略大于承插式桥墩,达到最大位移时的割线刚度差别很小。
(3)纵筋应变在承台顶面以下400 mm快速变化且达到屈服,该区域为承插式墩柱易损伤区域,需采取合理的构造措施加强保护。
(4)最小承插深度计算公式可用于指导承插式桥墩的抗震设计,其应用范围有待进一步理论和试验研究。尤其在高烈度地区,承插式桥墩的承插深度应大于本文计算所得最小承插深度。
需要指出的是,影响承插深度的因素很多,例如灌浆料的粘结性和强度、承台的强度和配筋。本文的关注点在桥墩本身的性能,对于灌浆料和承台考虑较少。针对承插深度的研究,尤其是高速铁路,仍需要进行更多、更深入的针对性试验研究。

