凸显“角度”价值，感悟度量本质

刘琳娜 谢红霞 刘加霞

摘 要：《角的度量》单元第一课时的教学，介绍古代器具的功能，让学生体会角度的价值，激发“度量角”的需求；基于“历史相似性”，让学生用“特殊角”量角，感受“单位越小，度量结果越精确”；在介绍360°分度体系的基础上，让学生数1°角、在量角器上找角，感受度量单位的累加，熟悉量角器的结构；借助现代生活情境，让学生再次感悟角度的价值。由此，为下一课时正确使用量角器量角、画角做好操作经验和思想方法上的积累与铺垫。

关键词：小学数学；数学史；角度；度量；单位累加

一、课前思考

角概念的本质在于角的大小（角度）。小学数学中，四年级《角的度量》单元是在二年级《初步认识角》单元的基础上学习规范地测量角，培养学生的量感。感悟角度在生产、生活中的作用，才能激发“度量角”的需求，进而体验定义度量单位以及创造量角器的必要性，感悟度量本质。

对此，我们思考了以下问题：（1）借助什么情境更能凸显角度的重要性，引发度量角的需求，同时渗透中华优秀传统文化？（2）在量角器产生前，古人是如何量角的？这些方法的本质是什么？是否在第一课时就直奔“用量角器量角”的主题？（3）量角器是如何产生的？学生用量角器量角会遇到哪些困难？怎样帮助学生突破这些难点？

现行各版本小学数学教材中，有的直接比较两个角的大小，没有设计引发度量需求的情境；有的借助“滑梯”情境引导学生关注角度的作用，这一情境虽然贴近学生生活，但还不能体现角度在生产、生活中的广泛应用，也不能让学生感受到劳动人民的智慧。事实上，早在两千多年前，我国古代科技典籍《考工记》一书就记载了古人在生产活动中如何处理所遇到的角度问题。因此，我们选择中国古代兵器、乐器、农具上的“角度”作为引入情境，既激发学生学习的兴趣，又让学生加深对中国传统技艺的了解，感悟劳动人民的智慧。

进一步查阅文献可知，中国古人对角度概念，首先是以矩（直角）为基础构造出一些特殊角，用特殊角来创生其他角度概念；随着利玛窦与徐光启合作编译的《几何原本》的传入，中国古人才真正从360°分度体系的角度认识一般意义的角，而量角器（《几何原本》中提到的“有度之圆界”）就是360°分度体系的产物。“历史为教学提供了一面镜子。”  ［1］ 从历史相似性的视角看，感悟度量本质有两条关键的路径：一是借助“特殊角”测量并刻画未知角度，二是通过1°角累加得到更多新的角度。

会用量角器量角只是一种基本技能，为了培养学生的量感，还必须让学生思考量角器是怎样形成的，理解量角的本质是“要量的角”与“量角器上的角”重合，量角器上的角是各个单位角“有序”累加得到的。由此就能知道学生量角时的真困难：在量角器上找不到角，难以将量角器上的角与要量的角叠合；量角器有两圈刻度，不知道何时读外圈、何时读内圈的刻度。突破这些难点，绝不仅仅是记住量角的口诀（点对点，线对线，从零开始看），再把口诀转化为操作的流程，而需要了解量角器的结构本质，看到量角器上“密布着”一个又一个的“角”。

因此，我们决定在《角的度量》单元的第一课时，不急于让学生用量角器测量角的大小，而创设“古人没有量角器怎么办”的问题情境，从“特殊角”入手，在“用小角量大角”的活动中引发学生对“单位累加”“度量值不够精确时要使用更小单位”等度量本质（思想）的深层次体验，继而介绍360°分度体系来得到1°角，通过“180个1°角累加”“在量角器上找角”等活动，让学生进一步认识度量本质，更为清晰地看到量角器的内在结构，为下节课正确使用量角器量角、画角做好铺垫。需要指出的是，几个版本的教材都设计了“用小角量大角”的活动，但是，其中要量的角都是锐角；我们用钝角替换教材中的銳角，

从而让学生可以用到“矩”（直角）这个特殊角进行度量。

基于上述思考，我们确定了本节课的教学目标：（1）能在了解古人兵器、乐器、农具功能的过程中，认识到“角的大小”决定了角在生活中应用广泛；（2）能在“用小角量大角”的活动中，体会度量单位的作用，感知单位越小度量结果越精确；了解1°角的产生过程，会用1°角的累加得到其他角度，形成和发展量感；（3）能经历量角器产生的过程，认识量角器的结构，会在量角器上找出大小不同的角，读出画在量角器上的角的度数；（4）能感受角度与古今生活的密切联系，体会数学学习的价值，培养数学的眼光和应用意识，感受古人的智慧。

二、课堂实践

（一）介绍古代器具的功能，体会角度的价值

师   生活中常常会用到“角”，在古代也是如此。 （出示下页图1—图4） 图1、图2是古代的两种兵器，分别叫作戈和戟；图3是古代的一种打击乐器，叫作磬，它被敲打后可以发出好听的声音；图4是古代的一种农具，叫作耒耜，用来翻土，播种庄稼。

（学生观察图片。）

师    图中的这些器具，在制造的过程中都用到了角度。 （同步指图） 比如，如果戈这个地方的角度太大，攻击敌人时就打不进去；如果角度太小，给敌人造成的伤害就太小。在农具的使用上，不同角度的耒耜适应耕种软硬程度不同的土地。看了这几幅图片，听了老师的介绍，你有什么感受？

生   生活中经常能看到角，制造不同的东西要用不同的角度。

师   看样子角度非常重要，生活中用到不同的角实际上是角度在起作用。

借助古人制造兵器、乐器、农具等应用角度的情境，让学生知道角度在生活中的广泛应用，激发学生对角度的兴趣。

（二）用“特殊角”量角，感受“单位越小，度量结果越精确”

师   古人要想制造这些器具，怎么确定这些角的大小？

生   可以用量角器量。

师   古代还没有量角器，怎么办呢？

生   可以用三角板上的角去量。

师   我们可以找到一些特殊的角来量一量。大屏幕上的图中标出了4个器具中的4个角。我们请一位同学上来选一个角，用三角板上的角来量一下。

（一名学生上台，选择了戟进行测量，她将三角尺上的直角与戟中标出的角进行了比对。）

生    用三角尺上的直角去量戟的这个角，刚好一样大，所以，戟的这个角应该是直角。

师   这位同学找到了三角尺上的直角，用两个角重合的方式量出戟的这个角也是一个直角。在我国古代并没有“直角”这个词， （同步板书） 直角被称为“矩”，钝角被称为“倨”，锐角被称为“句”。对于古人来说，在没有量角器的情况下，直角是一个特别重要的存在，很多角度都是在直角的基础上推导得到的。

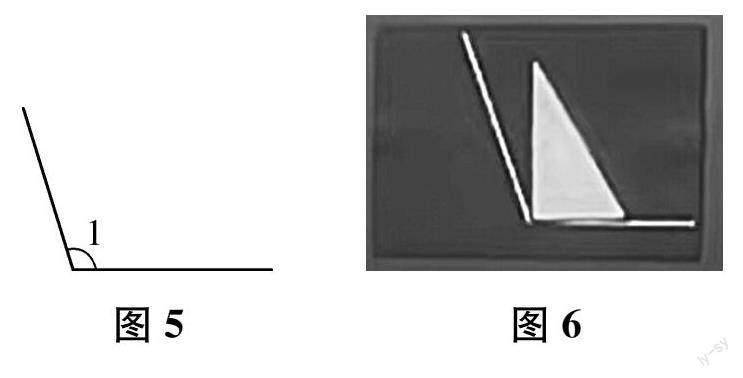
（出示学习单中的∠1，如图5所示） 接下来，请大家用三角尺上的角去量一量学习单上的∠1有多大，想一想怎样表达出、记录下你测量的结果。

（学生独立完成后同桌两人交流。）

师   谁来展示一下自己是怎么量的？完成这个任务的时候有什么困惑和问题？

生    （展示量法，如图6所示） 我发现用直角摆上去的时候，会缺一块，说明这个角比直角大。

生     （展示量法，如图7所示） 我摆了一个三角板的直角之后，又找了一个30°的角放上去，发现多了，说明这个角比90°+30°小一些。我估计了一下，可能是110°左右。

师   发现比90°大，又比90°+30°小一些，你为什么没有用两个直角来量呢？

生   用两个直角，差得太大了，不准确。

生    （展示量法，如图8所示） 我还有一种方法，不用直角了，都用比直角小的角，这样这个角的大小就是所用的三个角相加的结果。我发现，结果更精确了。

生   可还是有一点点缝隙，三角板上的角是固定的，不能调，所以怎么量都有误差。

生   还可以用更小的角。

师   就是把标准或者单位变得更小。

生   可以用量角器。

在用三角板上的幾个特殊角相加来表示未知角的过程中，再现了我国古人表示角的方法，让学生感悟度量的可加性，初步感知度量工具和度量方法引起的误差;同时，引导学生通过把单位变小来得到更为精确的度量结果，培养学生的量感。

（三）借助量角器上的1°角，介绍角的360°分度计量体系

师   有同学提到了量角器，为什么用量角器量会更精确呢？是因为量角器上有什么？

生   有刻度线。

生   有小格，就像1厘米、1毫米一样。

生   有1°角。

师   1°角是如何产生的？

生   把一个圆平均分成360份，1份就是1°。

师   意思到了，但是表达不够准确。

（教师播放视频，介绍西方天文学上角的360°分度计量体系，让学生感受到：有了统一的、更小的1°角这个单位，度量结果更精确。）

生   我发现，量角器上，10°对着的大约是1厘米，那1°就大约是1毫米。

师   角不能用一个固定的长度来表示哦。

顺应学生在把度量单位变小的基础上想到的量角器，提问“为什么用量角器量会更精确”，引发学生对量角器结构的思考。抓住学生回答的1°角，引出360°分度计量体系。这时，一名学生想到用角对应的弧长（也可能是弦长）来刻画角的大小，但是，教师没有听懂，直接否定了该学生的想法。实际上，中国古人的“以规生度”就是用“弧长”表示“角度”的。如果教师能肯定学生的想法，鼓励学生在课后或在今后的学习中继续研究“长度能否表示角的大小”这个问题，就能为学生找到思维的生长点。

（四）数1°角，感受度量单位的累加

师    回忆一下，我们在测量长度时，找到的单位长度是1 cm、1 dm、1 m……在测量面积时，找到的面积单位是1 cm 2、   1 dm 2 、

1 m 2……所以刚才有同学联想到了角的度量可以选择1°角作为度量单位。这个想法可真棒！我们把1°角进行累加，看看会发生什么？

（教师出示1°角。）

生   1°角太小了！

（教师累加5个1°角，同时让学生计数，得到“5个1°是5°”的结论；继续累加，继续计数，得到“10个1°是10°”；然后10°、10°地累加得到180°。教师让学生指认所有角的顶点，学生知道顶点就在半圆的中心。这时，教师才呈现出量角器。整个过程如图9所示。）

度量的本质是单位的累加。带领学生从1°角到180个1°角，开展数角及找角活动，初步感受角的大小是1°角的累加；再借助180个1°角累加起来的模型，初识量角器的结构，初步感知量角器上的角。

（五）在量角器上找角，熟悉量角器的结构

师   刚上课就有同学说用量角器量角，量角器就是测量角的大小的工具。观察一下量角器，上面都有什么？

生   量角器上有数，有刻度。

师   外面这圈叫外圈刻度，里面这圈叫内圈刻度。为什么会有两圈刻度呢？

生    （上台同步比画） 量的时候，如果角冲这边，就从这边开始数；如果从角冲那边，就从那边开始数。

师   角的大小就是1°角的累加，我们在数刻度的时候要看清楚1°角在哪里，从哪个方向来数。量角器上还有什么？

生   量角器上还有许多线。每一条线都对应着相应的刻度。

（教师布置在量角器上找角的任务：①在量角器上找出一个30°的角，说一说你是怎样找到这个角的；②在量角器上任意找出一个角，并在印着量角器的学习单上画出来。学生活动。）

生    （上台同步比画） 我是从左边0刻度线开始，

（顺时针） 数出30°的。

师   还有别的方法吗？

生   我从30°开始找，数到60°，这个角也是30°。

师   这说明我们不一定要从0刻度线开始找，而只要通过累加数出30°就可以了。谁来展示一下画出的角？

（一位学生展示了如图10所示的角，引发了争议：有同学说是150°，有同学说是30°。）

师   到底是多少度？

（多数学生认可是150°。）

师   为什么是150°？

生   因为开口冲左，所以读外圈。

师   读的时候，我们要看是从哪里开始数、沿哪个方向数。

对这个角，我们要从0刻度线顺时针一直数到150°。能读30°吗？

生   不可能是30°，因为一看就比直角大。

师   对！通过与直角比较，也能判断这个角不可能是30°。

（教师又邀请几位学生展示自己画出的角，读出角的度数。）

用量角器量角就是将“要量的角”与“量角器上的角”重合。学生之所以在量角时出现困难，是因为找不到量角器上的角，或不知道应该顺时针还是逆时针读出度数。为了破解这个难点，教师基于学生数角的经验，设计在量角器上找角的活动，帮助学生进一步感受角的大小是1°角的累加，熟悉量角器的构造，从而合理得到度量结果。教师还借助学生读数错误、产生冲突的契机，再次帮助学生澄清了从哪里开始数，沿哪个方向数。

（六）借助現代生活情境，再次感悟角度的价值

师   角度在古人的生活中很有用，在我们现在的生活中应用也非常广泛。请你举出生活中的实例。

（学生举出建造大楼、发射火箭等都需要用到角度。）

师    （出示图11） 这是什么？

生   是滑雪的雪道。

师   对。北京刚刚成功举办了冬奥会，很多同学对雪上项目都有一定的了解。结合刚刚的学习经验，请你估一估两种

雪道这两个角的度数分别是多少度？

生   30°、45°。

（教师抽象出雪道中的角，给出角的确切度数，分别是20°和45°。）

师   雪道的角度是有一定标准的。哪位同学来读一读关于雪道的小知识？

生    （朗读） 一般来说，初级道（绿道） 14°以下，中级道（蓝道） 14°—21.8°，高级道（黑道） 21.8°以上。大众滑雪

雪道的角度原则上限制在30°之内。

师   请你根据这个标准判断两个雪道分别属于什么级别的雪道。

生   1号雪道属于中级道，2号雪道属于高级道。

师   角度是判断雪道级别的依据。生活中很多地方都

会用到角度的知识，比如椅背的倾斜角度、无障碍通道与地面形成的夹角，等等。课

后，同学们可以自己去查阅资料，看看这些角是多少度。只要用数学的眼光去观察生活，就会发现生活中有很多的数学奥秘。

现代生活中应用角度的真实情境与课始

引入的古人生活情境起到呼应作用，帮助学生感悟角度从古至今都在生活中发挥着重要的价值，再一次意识到角度的重要性；也搭建了数学与生活之间的桥梁，培养了学生用数学的眼光观察现实世界的意识与能力。

三、课后反思

本节课借鉴古代数学中角度概念和角度计量的发展历史，将古人认识角度的路径与学生认知角度的难点建立联系。从介绍古人制造的器具的特点入手，极大地引发了学生的学习兴趣。“用特殊角量角”的活动再现了古人用特殊角来刻画其他角度的思想，让学生体会到度量单位产生的价值。

本节课的目标并不停留在量角的操作技能层面，而从度量的思想本质出发，重在落实学生量感的培养。教学中，我们深刻地感受到，数学发展史中蕴含着大量可利用的、有价值的教学资源。对此，教师不能仅仅是“告知”，而需要在深刻理解数学本质和发展脉络的基础上，有意识地筛选和挖掘史料的教学功能和文化价值，尤其是结合课标与教材要求进行合理的设计，以学生可接受的方式呈现。

数学文化在小学数学课堂中的融入既可以有明线（史料），也可以有暗线（思想方法）。本节课中，学生尽管还没有真正用量角器去量角（这个内容设计在下节课），但是，犹如庖丁解牛，已经对量角器的结构有了较为全面的认识，对度量方法的本质有了较为深刻的理解，为后续量角、画角从操作经验到思想方法都做好了积累与铺垫。

参考文献：

［1］ 汪晓勤.HPM视角下的小学数学教学［J］.小学数学教师，2017（7/8）：77 83+2.