拟MQ函数在物探数据处理中的应用

张一凡,刘海飞,柳建新,郭 鹏,刘 昕

(1.中南大学 地球科学与信息物理学院,长沙 410083;2.有色资源与地质灾害探查湖南省重点实验室,长沙 410083)

0 引言

地球物理观测的数据都可视为空间、时间域离散的数字信号。在点距稀疏不均匀(如航空物探)、因客观条件造成数据缺失(如地形因素)、仪器设备不稳定造成部分坏记录的情况下,往往需要通过有效插值方法尽量规律性补足观测数据集。另外,为避免数据解释得到错误的认识,强噪音引起的异常数据需在数据处理中剔除,并尽量采用一种保光滑、保形状的插值方法对真实数据进行恢复。线性插值、样条插值等常规插值方法在地球物理数据处理中应用广泛,但对于一些特殊场景,其插值光滑效果还需改进。

MQ函数(Multi-quadric function)最早由Hardy[1]于1971年提出,Franke[2]发现在29类散乱数据插值中,MQ函数的精确性、有效性、稳定性优于其它方法,然而利用MQ函数需要求解线性方程组且系数矩阵通常是病态的。因此,对MQ函数进行某种近似且避免求解线性方程组的方法逐渐引起重视,这种逼近函数被称为拟MQ函数。Beatson 和 Powell[3]利用 MQ 函数提出了三种单变量的拟MQ插值算子QA、QB、QC,并得到了它们的误差,同时证明拟插值算子QC具有很好的线性再生性和插值精度。Wu和Schaback[4]对QC进行改进,提出了一种新的拟MQ插值算子QD,并讨论了它们的逼近阶和保形性。后来,该插值算子被广泛应用于求解偏微分方程[5-9]。此外,Ling[10]在Wu和Schaback工作的基础上,提出了一种多水平单变量拟MQ插值算子。Ling[11]还利用空间维数分离方法,构造了拟MQ插值算子QR。Jiang等人[12]在拟插值算子QD的基础上构造了一种高精度的拟插值算子QW,该算子具有保线性且具有很高的精度。高文武[13]讨论了基于导数信息的拟MQ插值的构造方法,并用该方法构造了一个拟MQ插值算子,证明了该算子的收敛性及保形性。

拟MQ函数无需求解线性方程组,根据离散节点能快速直接给出插值结果,还具有良好的保形性、计算稳定、计算量小等优点。因此,在过去的几十年里,拟MQ函数取得了一定的发展[14-16]。但整体而言,该函数在地球物理领域的应用研究较少。

笔者利用Wu和Schaback[4]提出的拟MQ插值算子QD,分析整理了其在物探数据处理中的应用,主要包括拟合地表高程、高密度电法数据插值与平滑、电测深曲线插值与求导等,取得了良好的处理效果,证实了该函数在物探数据处理中的有效性和实用性。

1 基本理论

1.1 MQ函数

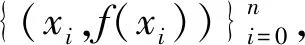
f(xj),j=0,1,…,n

(1)

式中:φ(x-xi)为MQ函数,对于一维插值问题,其形式为:

(2)

式中:s为形状参数,决定了曲线的锐度。若相邻插值结点的最大间隔为h,s相对h保持相关且趋于零可获得更高的准确性[1]。将式(1)写成矩阵形式:

Ac=z

(3)

其中:

A=

求解线性方程(3),即可求得解向量cn×1。将解向量cn×1及待插点xj代入式(1),便可计算出待插点xj的值f(xj)。

1.2 拟MQ函数

为避免求解线性方程组,Beatson 和 Powell[3]利用 MQ 函数提出了三种单变量拟插值算子QA、QB、QC。Wu和 Schaback[4]在此基础上给出了逼近阶和保形性较好的拟插值算子QD。

(4)

拟插值算子QB满足:

f(xn)βn(x)

(5)

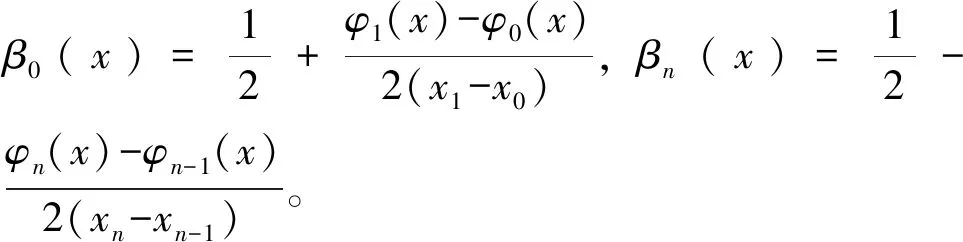
f(xn)αn(x)

(6)

为了进一步提高插值精度,相较于拟插值算子QA和QB,还可以引入更多条件定义拟插值算子QC:

QCf(x)=QBf(x)+f′(x0)γ0(x)+

f′(xn)γn(x)

(7)

将其改写为:

QCf(x)=f(x0)β0(x)+f′(x0)γ0(x)+

f(xn)βn(x)

(8)

Beatson 和 Powell[3]对三种拟插值算子进行了大量测试,表明QC的插值精度最高。但应用QC需要事先知道边界点的导数,实际应用中很难满足此条件。为克服这一缺点,Wu和Schaback[4]对其进行改进,定义了一种具有保单调性和保凸性且不需要知道边界点的导数值的拟插值算子QD,它的逼近效果与QC相当。拟插值算子QD的定义如下:

QDf(x)=f(x0)a0(x)+f(x1)a1(x)+

f(xn-1)an-1(x)+f(xn)an(x)

(9)

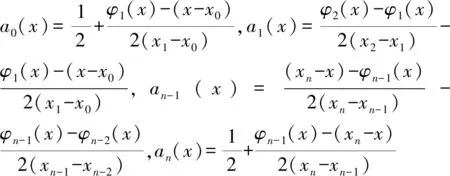
可将式(9)展开为:

(10)

由于大量实际工程数据均无法给出插值端点处的导数值,相比之下QD具有更好的应用价值。

1.3 拟MQ函数的导数形式

常规插值方法往往只保证函数值插值精度,但很多地球物理方法需要对数据的数值微分进行分析以突出弱异常,这对插值方法提出了更高的要求。对于式(10),其一阶导数为:

QDf′(x)=

(11)

二阶导数为:

(12)

通过式(11)、式(12),便能推算出离散点的导数值,从而在观测曲线中发挥提取弱异常的优势。

2 拟MQ函数在物探数据处理中的应用

2.1 在地表高程插值中的应用

以山东某金矿地球物理勘查剖面的地表高程数据为例,该剖面已知的地表高程点有64个,横向分布范围为[0～4 460],并且呈不等间距分布。以10 m为间隔从0到4 460均匀采样作为待插结点,采用三次样条函数及拟MQ函数对地表高程点分别进行插值。插值结果如图1、图2所示。

图1 三次样条函数的插值结果Fig.1 Interpolation results of cubic spline functions

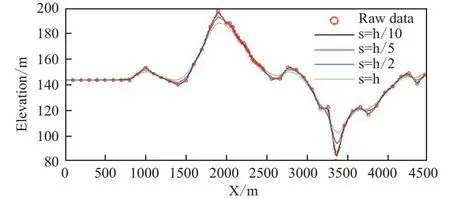
图2 拟MQ函数的插值结果Fig.2 Interpolation results of quasi-MQ functions

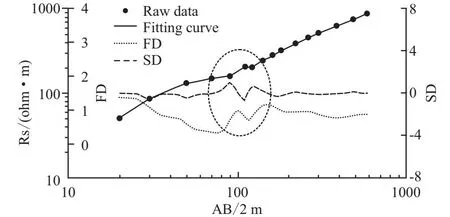
可以看出:在利用三次样条函数进行插值时,当函数值变化较大且插值结点较稀疏时,会在插值结点附近引起插值曲线的震荡(如3 160 m～3 260 m),而拟MQ函数则避免了这一缺陷。当形状参数s=0时,插值曲线与原始高程曲线完全重合。当s相对h(相邻插值结点的最大间隔)逐渐增大时,插值曲线在阶跃点处的光滑程度也随之增大,但总体形态与原曲线保持一致。因此,说明拟MQ函数具有良好的保形性和保单调性。对于形状参数s的选择问题,目前没有一个量化的选择依据,但为了获得更高的准确性,s与h保持相关且趋于零时是最有利的[1]。若将拟MQ函数用于高程拟合,形状函数不宜取得过大(s

2.2 在高密度电法数据处理中的应用

在高密度电法勘探中,常常因电极接地电阻过大或浅地表不均匀体的影响,使得观测数据含有一定程度的干扰噪声(浅部因素也会影响深部数据)。在布设的电极阵列中,同一根电极可能会作为供电电极或测量电极,如果某个电极接地电阻大,对于供电回路,将导致供电电流不稳定对于测量回路,将产生读数不稳定,直接影响着数据的观测精度,最终造成绘制的视电阻率拟断面图存在虚假或冗余异常。为压制高密度电法数据的干扰噪声,笔者尝试采用拟MQ函数对高密度数据进行降噪处理。

以邵怀高速公路某段高密度电法勘查为例,以检验拟MQ函数的降噪效果。该勘查段测线长度595 m,120道电极,点距5 m,测量层数39层,图3(a)为原始高密度数据绘制的拟断面图,可以看出在断面图中存在较多冗余异常。采用拟MQ函数对该数据断面进行逐层降噪处理,考虑高密度电法的观测特点,以观测点距(5 m)作为形状参数,图3(b)为处理后的高密度数据绘制的拟断面图,从断面图中可以看出,视电阻率等值线的平滑特征得到明显改善,更有助于数据分析和解释。

图3 高密度视电阻率断面处理前后对比图Fig.3 Comparison before and after HD apparent resistivity section procession

2.3 在电测深曲线数据处理中的应用

由于利用数值微分可以提取地球物理原始数据曲线中的弱异常信息的特点,对新疆清河县地下水的分布情况研究分析。以其中一条电测深曲线为例,利用拟MQ函数对其进行计算一维加密插值(Fitting curve),进而获得更可靠的一阶导数(FD)和二阶导数(SD),具体如图4 所示。

图4 基于拟MQ函数的电测深数值微分曲线Fig.4 Numerical differential curve of electrical sounding based on quasi-MQ function

可以看出:在极距AB/2为90 m和125 m的位置存在微弱的低阻异常,通过对电测深曲线计算一维插值、一阶导数和二阶导数,使这两个位置的弱异常幅度得到增大。结合该区地质资料及钻探施工条件,在此处开展了钻孔工作。发现在深度20 m以内为第四系,20 m～75 m以内为凝灰质砂岩,75 m～130 m以内为花岗岩,在深度130 m处打到构造破碎带,含水量较大,由于水压过大导致冲击钻探方法难于施工,并于135 m深度处终孔,未打穿断层破碎带,终孔孔径110 mm。采用32 m3/h水泵进行抽水试验,静水位2.1 m,动水位28 m,水位降深25.9 m,经计算该钻孔出水量为46.3 m3/h(1 111.2 m3/d)。因此,利用拟MQ函数可以较好提取物探原始数据曲线中的弱异常信息。

3 结论

通过拟MQ函数在物探数据处理中的应用研究,得到以下结论:

1)利用拟MQ函数拟合地表高程,整体曲线较光滑,能很好地逼近地表形态,并随着形状参数的增大光滑程度加大,仍能保留原始数据的整体特征,验证了拟MQ函数具有良好的保形性及保单调性。

2)利用拟MQ函数对高密度数据进行插值平滑处理,能达到很好的降噪效果,从而有利于后续数据的分析与解释。

3)利用拟MQ函数对电测深曲线进行插值、一阶求导、二阶求导处理,能明显放大地下弱异常的幅度,有利于提取物探原始数据曲线中的弱异常信息。

随着理论研究和工程实践的共同进步,拟MQ函数有望在地球物理数据处理中发挥更大作用,显示出更多优势,成为一种常规数学工具。