基于Attention-UNet网络的速度模型构建方法研究

孙德辉,王云专,王莉利

(1.东北石油大学 地球科学学院,大庆 163318 2.东北石油大学 计算机与信息技术学院,大庆 163318)

0 引言

地震数据的高精度处理与解释的关键是如何取得高精度的地下速度模型,通常用于建立速度模型的方法有层析成像[1]和全波形反演[2]两种方法。然而,层析成像和全波形反演都是耗时的,需要大量的计算,并且严重依赖于人机交互和质量控制。所以如何构建精确的速度模型也面临着各种挑战。当前最流行的方法就是全波形反演[3],全波形反演通过局部优化算法来最小化模拟数据与实际地震数据的差异,从而推断产生该模拟数据的高精度速度模型就是地下真实速度结构。自从上世纪Tarantola[2]和Lailly[4]使用伴随震源法高效计算了梯度更新值后,关于全波形反演的研究便一路火热至今。但全波形反演在实际生产应用中却有着一个始终无法避免的问题,那就是全波形反演是强非线性方法,它极其依赖初始条件,包括算法开始时的初始速度模型和实际地震信号中的低频分量[5-6]。目前国内外的攻克方向大致可分为两种:一是从算法本身入手,尽可能降低全波形反演的非线性;另一种是从数据与模型入手,想办法提供良好的初始速度模型和准确的低频分量。

深度学习(Deep Learning,DL)[7-8]是机器学习(Machine Learning,ML)的一个新分支,在图像和语音处理方面表现出了突出的识别和分类性能[9],引起了广泛的兴趣。Zhang等[10]建议使用神经网络从地震道中自动预测断层。周传友等[11]采用BP神经网络方法,提高了单井岩相预测的准确性。Araya-Polo等[12]采用速度谱作为数据集,基于常规的卷积神经网络提出了一种将深度学习引入地震速度建模的方法。Jia等[13]提出一种基于蒙特卡洛的方法以降低训练数据集,通过选取部分地震数据集来更高效的训练网络。Wang等[14]利用全卷积神经网络,通过对原始多炮数据进行盐体检测,比传统方法更加快速、有效。Mosser等[15]基于深度卷积生成对抗网络的深度学习方法,将反演问题看作不同域之间的转换,实现了地震数据域与速度模型域之间的转换。Li等[16]基于深度神经网络的地震反演网络(SeisInvNet),使用所有地震道数据和全局地震剖面重构速度模型。Zhang等[17]开发了一种基于实时数据驱动技术的速度建模对抗网络(VelocityGAN),用以提高速度模型精度。Yang等[18]基于FCN提出了直接使用全波形地震数据建立速度模型的方法。Yuan等[19]在已知初始速度和数据的情况下,用全卷积神经网络(Full Convolution Neural Network,FCN)实现了时移数据与目标速度变化之间的映射。

笔者利用数据驱动思想,提出一种基于Attention-UNet网络的速度模型构建方法。通过对Attention-UNet网络模型优化,提高模型精确度,防止过拟合。实验包括两个阶段,在训练阶段中,将多炮道集一起输入网络,有效地逼近了数据与相应速度模型之间的非线性映射。在预测阶段中,利用训练好的网络,输入新的地震数据,获得预测的速度模型。

1 方法原理

1.1 改进UNet网络架构

从地震道建立速度模型具有挑战性,因为它涉及从地震道(x-t)到空间/模型域(x-z)的数据转换,这构成了一个反问题。神经网络能够逼近连续函数直到指定的精度,这为这项研究提供了理论基础。

利用深度神经网络来构建地震信息和速率模型之间的映射关系,可以实现基于深度学习的地震速度建模。FCN用卷积层代替了传统卷积神经网络的全连接层,支持任意大小的输入数据,实现图像识别领域单个像素点的准确预测[20]。基于FCN的改进UNet具有“U”结构的编码和解码。 它首先通过下采样提取输入数据的特征,然后通过上采样将特征信息传输到分辨率更高的后面层,以获得更精细的结果[21]。地震速度建模是一个从地震数据中提取地下速度信息的过程,这与UNet提取输入数据特征信息的特点非常一致。因此,为了从原始地震数据中实现地震速度建模,我们采用并修改了UNet架构,并在UNet网络的基础上,在每个跳跃链接的末端,使用Attention Gate[22]结构,对需要提取的特征实现Attention机制。注意力机制结构如图1。注意力机制是模仿人类注意力而提出的一种解决问题的方法。它可以从大量的信息中过滤出高价值的信息,让模型专注于有价值的特征。Attention-UNet 主体架构与 UNet 网络一致,网络结构如图2。(不同颜色的矩形代表神经网络的不同层。其中,蓝色代表卷积层;橘色代表池化层;绿色代表上采样层;蓝色矩形(卷积层)中的红色虚线代表裁剪操作;矩形的左侧数字代表层的大小;下侧数字代表层数;左图代表反射波形数据,右图代表地震速度模型,红色箭头代表改进位置,其它箭头代表层与层之间的操作。)

图1 注意力机制模块Fig.1 Attention mechanisms module

图2 改进后的UNet模型网络结构Fig.2 Improved UNet model network structure

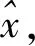
在Attention-UNet的基础上,笔者主要做了两点修改,以适应地震速度模型的构建。首先,鉴于输入地震数据和输出速度模型之间的不一致性,利用Attention-UNet实现了不对称尺寸之间的映射。常用于图像识别的Attention-UNet的输入和输出是在图像域,需要相同的大小。然而,地震速度建模的输入数据是在时域,而输出的速度模型是在深度域,这就导致了输入和输出数据的不匹配。在基于深度学习的地震速度建模过程中,地震数据被映射到速度模型中,输入和输出数据的不匹配会导致神经网络的输入和输出的大小和存储方式的明显差异,因此神经网络很难完成训练。为了解决这个问题,笔者在应用损失函数之前,将最终输出层截断到与输入神经网络的速度模型相同的大小。其次,为了处理地震数据,我们指定了不同的炮点道集,这些道集在不同的震源位置生成,但来自相同的模型,作为输入通道。因此,输入通道的数量与每个模型的震源数量相同。将多炮点地震数据同时输入网络,提高了数据冗余度。该网络的输入是由29个大小为400×301的地震反射波形数据和与之对应的速度标签模型。神经网络的输出是大小为201×301的二维地震速度模型。网络主体与原始的UNet相似,共使用了22个卷积层(蓝色矩形)、4个池化层(橙色矩形)、4个上采样层(绿色矩形)和1个裁剪层(红色虚线)。卷积层采用Relu激活函数,卷积核大小为3×3,最大池化层的下采样因子和采样层的上采样因子大小都为2×2。深度神经网络有四个下采样过程和四个上采样过程,即保证网络有足够的深度提取速度特征,又不会使网络模型过于复杂。

1.2 相关公式

利用地震数据作为直接输入来估计速度模型,网络需要将地震数据从数据域(x,t)投影到模型域(x,z)地震数据,该方法的基本思想是建立输入与输出之间的映射关系,映射关系可以表示为:

(1)

网络通过最优化方法迭代求出损失函数的最小值,从而训练出最佳的网络模型。这个过程可以表示为:

(2)

(3)

需要注意的是,损失函数不同于FWI中的目标函数,表达式如下所示:

(4)

式中:δd为模拟数据dcal和观测数据dobs之间的残差,dcal为模拟数据,dobs为观测数据。

为了加速收敛,笔者采用Adam梯度下降法[23]来优化算法模型,其具有较短的收敛时间,对于大型数据集机器学习的问题有较好的鲁棒性。

2 训练集的构建和数据集

2.1 数据准备

为了训练一个有效的网络,需要一个合适的大规模训练集。在典型的FCN模型中,训练输出由一些标记图像提供。笔者采用二维合成模型对神经网络模型进行测试。数值实验提供了一种速度模型,即二维模拟模型,每个速度模型都是唯一的。

2.2 训练集模型

将地震速度模型作为深度学习的标签,即深度神经网络的输出;将地震波形及其速度标签作为深度学习的数据集,即深度神经网络的输入,可以构建深度神经网络的训练集。

在本节中,我们将使用合成数据测试提出的算法。采用1 500个二维盐体模型样本,其中抽出200个具有代表性的模型用于测试,并将其余的1 300个作为训练样本。每个模型有5～12层作为背景速度,每层的速度值从模型地表到底层由2 000 m/s到4 000 m/s逐渐增加。将具有任意形状和位置的盐体嵌入到每个模型中,盐体的恒定速度为4 500 m/s。所有的模型大小相同,为x×z=301×201的格点,空间间隔为h=10 m。图3显示了来自数据集的4个具有代表性的模型。

图3 训练数据集中的4个样本数据Fig.3 Four sample data in the training data set

根据训练集中的地震速度模型,通过时域交错网格有限差分格式求解含15Hz 雷克子波的声波方程,时间方向采用二阶,空间方向采用十阶,放置震源数量的多少影响训练的计算时间,同时合并更多的炮数可以降低过度拟合的风险[24]。我们对于每个模型,从(z,x)=(0.2,0.0)km到(0.2,3.01)km均匀地放置29个震源,依次模拟炮点集。同样,从(z,x)=(0.2,0.0)km到(0.2,3.01)km均匀地放置301个检波器,用来接收地下信号记录。正演建模的详细参数如表1所示。采用完美匹配层(CPML)吸收边界条件[25]应用于所有四个网格边缘,以减少不必要的反射。图4显示了由图3中的第一个速度模型生成的地震数据的六炮。

表1 有限差分正演的参数Tab.1 Parameters of finite difference forward modeling

图4 有限差分格式生成的地震数据的六炮Fig.4 Six shots of seismic data generated by finite difference format

2.3 测试数据集

由于使用了监督学习方法,测试数据集的速度模型具有与训练数据集相似的地质结构,岩体分别位于地层的中间和地层的底部。所有用于预测的速度模型都没有包含在训练数据集中,并且在预测过程中都是未知的。采用与生成训练数据集输入相同的方法获得用于预测的输入地震数据。

3 数值实验与结果分析

3.1 实验环境

笔者的实验环境主要由软件和硬件两部分构成,其中硬件方面:CPUIntelXeonSliver4210@2.20 GHz内存500 GB,显卡 GeForce RTX 2080。软件方面:选择使用的语言为Python和Matlab,深度学习框架为Pytorch,开发环境是Pycharm和Matlab R2014a,分别用于实现网络模型搭建和运行FWI,操作系统为RedHat Linux 8和Window 10。具体实验环境数据见表2。

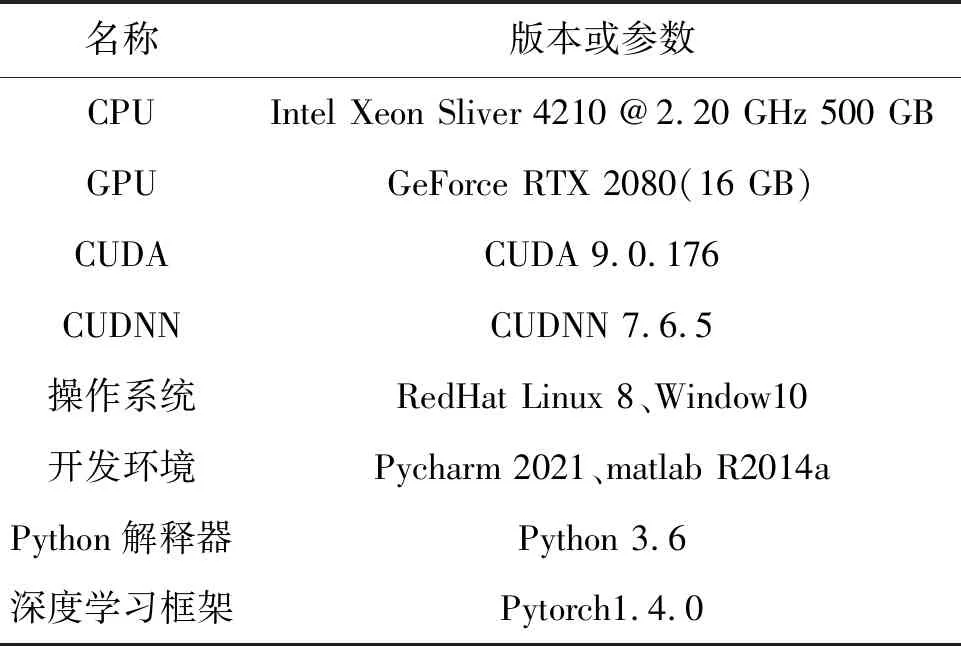
表2 实验环境Tab.2 Experimental environment

3.2 模拟数据集的反演

对二维模拟速度模型进行了第一次反演。在训练阶段,从训练数据集中随机选取201×301速度模型尺寸的8个样本,构建每次迭代的训练批次。在保留地震数据主要特征信息的前提下,将每批数据的一炮地震数据尺寸降采样至400×301,减少计算量的同时提取大尺度的特征信息。降采样前后的一炮地震数据如图5所示。训练时,采用的迭代次数(Epochs)为80次,批大小(Batch Size)为8。参数如表3所示。

表3 网络训练参数Tab.3 Network training parameters

图5 经过降采样前后的一炮地震数据Fig.5 Seismic data of one shot before and after down sampling

训练的计算时间与地震道的大小和训练样本的数量成正比,也与通道的数量和网络的复杂性有关。为了验证炮集对网络模型训练的影响,我们分别训练均匀放置10个震源和29个震源的数据集作为输入来训练网络。

同时为了反映添加注意力机制对网络学习过程的影响,在不添加注意力机制的传统UNet网络上使用相同的地震数据,即数据集数据。由于Attention-UNet网络编码器和解码器主体结构和UNet一致,所以二者这一部分的参数设置是一致的,如:网络深度都是4层;卷积核大小以及激活函数一致。图6显示了在学习过程中的标准化损失或预测速度值与真实速度值之间的均方误差。图6(a)为震源对于网络训练的影响,图6(b)为Attention-UNet网络和UNet网络对模型训练的影响。

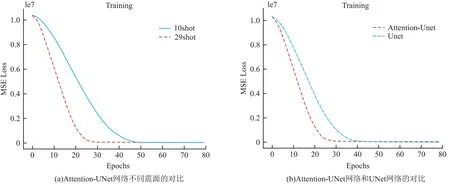
图6 学习过程中的标准化损失或预测速度值与真实速度值之间的均方误差Fig.6 Standardization loss or mean square error between predicted speed value and real speed value in the learning process

在图6(a)中,29个震源网络的收敛速度比10个震源网络的收敛速度快。图6(b)中可以很明显的发现Attention-UNet网络模型迭代20次后loss曲线已趋于平缓,而UNet则是在迭代40次以后loss曲线才趋于平缓。分别计时两个网络的训练时间,Attention-UNet网络训练时间是148min,UNet网络的训练时间是190 min,从上述实验结果表明,Attention-UNet网络模型对学习过程来讲更快的收敛速度,从而减少了训练时间。

验证定量评估Attention-UNet的性能,我们通过峰值信噪比(Peak Signal to Noise Ratio,PSNR)[26]来评价模型预测的效果。如表4所示,UNet和Attention-UNet相比,Attention-UNet在测试数据集上获得了更高的平均 PSNR,这说明 Attention-UNet对模型的预测结果是好的。

表4 测试集的平均PSNRTab.4 Average PSNR of the test set

为了显示网络的演变过程,笔者在训练过程中捕获了一组数据,展示了整个训练过程,如图所示,图7(a)是标签,是我们期待网络输出的模样,也是我们其中的一次测试样本,图7(b)、7(c)、7(d)分别是我们构建网络迭代训练的10次,30次,60次的即时输出,从中可以看出模型越来越接近我们的真实样本。

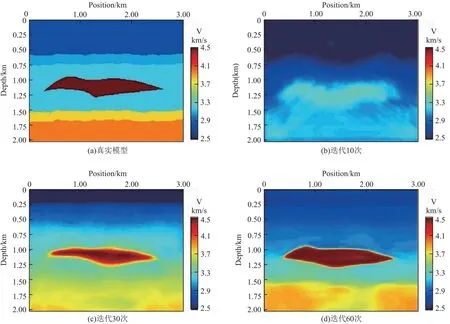
图7 训练追踪Fig.7 Training tracking

最后是对训练后的网络对测试数据进行预测,将200组测试数据一次性输入之后,只需要几秒钟就可以完成输出预测,从时间效率来看,我们的预测时间要远远优于全波形反演。为了验证网络输出的速度模型与真实模型之间是否相近。我们的方法与FWI进行了比较。在时域正演模拟中,我们使用与生成训练地震数据相同的参数设置。采用多尺度频域反演策略,反演频率选择1 Hz～20 Hz中12个进行反演。本实验采用伴随状态法求取梯度,应用L-BFGS(Limited-memory BFGS)优化算法更新模型。FWI的观测数据与我们用于预测的地震数据相同。共设置29炮震源激发,均匀分布于地表水平方向0.2 km～2.9 km范围内。每炮301道接收,检波点均匀分布于地表水平方向,不随炮点移动。反演迭代次数25次。另外,以高斯平滑函数平滑后的真实速度模型作为FWI的初始速度模型。图8显示了用于测试的代表速度模型,图8(a)表示真实模型,图8(b)显示了高斯平滑后的初始模型,图8(c)表示网络预测模型,图8(d)显示了FWI的结果。

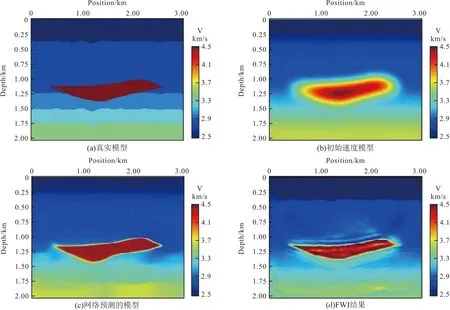
图8 不同方法反演结果对比Fig.8 Comparison of inversion results of different methods

为了定量分析预测的准确性,我们选取了两个水平位置x=1 km和x=2 km,并在图9所示的速度与深度剖面中真实模型(蓝色)的速度值、预测(橘色)的速度值。

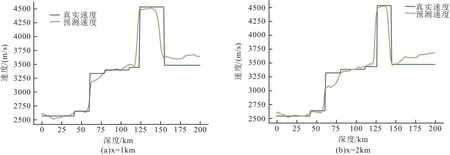
图9 垂直速度剖面Fig.9 Vertical velocity profile

图8展示了和全波形反演方法的对比,笔者的方法(图8(c))和全波形反演(图8(d))的方法都可以较准确的确定速度模型中高速盐体的位置和形状,全波形反演在迭代25次的情况下,盐体刻画的不够清晰,还有一些较明显的假象。由于实际标准地震数据集的限制,在图8(a)和8(c)两者之间存在对速度细节刻画不够精确的情况。

图9做了速度模型特定位置的速度剖面,抽取了图7中水平位置1 km和2 km的两个速度剖面进行对比。由此图可以看出,笔者方法的速度建模结果较为准确。

4 结论

笔者通过地震反射波形和速度标签建立数据集,构建了一种有监督深度学习速度建模方法用于反演。对层状砂体模型的数值实验结果显示,深度学习速度建模方法结合地震反射数据和速度标签训练集可以有效地重建模型的主要特征。认识和结论如下:

1)使用多道地震波形和速度标签作为深度学习的特征数据集为速度模型预测提供了冗余信息,降低了过拟合的风险和计算难度。

2)通过将加入注意力机制的U-Net作为深度神经网络框架,提高了网络模型的收敛速度和速度模型预测的准确性。

3)与FWI相比,一旦网络训练完成,重构成本可以忽略不计。此外,损失函数在模型域内进行测量,利用网络进行预测时不产生地震记录。所以不存在FWI的“周期跳跃”问题。