以共反射点为目标的二维射线追踪方法研究

刘军胜

(中石化地球物理有限公司,北京 100000)

0 引言

地震资料采集的过程中,目的层的有效覆盖次数是影响资料信噪比和成像效果的关键因素,资料信噪比与覆盖次数的平方根成正比。技术人员一般利用照明分析,射线追踪模拟方法解决地下复杂构造形态下覆盖次数均匀性问题,而其中射线追踪方法是最普遍的方法[1-4]。射线追踪自上世纪70 年代首次提出至今,以不同的数值计算方法为关键技术,以计算描述地震波运动学特征的相关参数(走时、射线路径)等为核心目标,相继提出了十多种方法[5]。当前最常用的射线追踪的方法为试射法、迭代法、波前追踪法,地震勘探采集设计软件的射线追踪模块主要基于以上三种方法。KLSEIS软件的二维射线追踪模块综合运用了试射法和迭代法,MESA软件运用了波前追踪法,OMNI则基于试射法。三种方法计算精度和计算速度存在较大的差异[6-9]。例如试射法的计算精度主要取决于设定的入射角度范围和增量,迭代法的计算精度则受计算网格大小的影响。复杂构造形态条件下,若参数设置不合理,各种方法均存在遗漏路径的问题。计算精度较高的迭代法在穿越相同炮检点存在多路径时,仅能计算一条路径,同时无法限定反射和入射角范围。由于漏解、精度的问题,常用的设计软件射线追踪模块均缺少覆盖次数计算功能。更为关键的是,常用的射线追踪方法直接计算地震波自激发点到接收点的路径,限制了研究人员查找和判断影响目的层关键区域的炮集或道集。设计人员利用设计软件射线追踪模块仅能查看目的层区域射线的稀疏和稠密程度,发现问题,无法给出明确的解决方案。设计人员需要借助其他方法或是通过不断的调试来查找影响问题区域的炮检点进而解决问题。专业模型软件Tesseral Pro在这一方面有所改善,可以查看目的层选定段的所有射线路径。但Tesseral Pro仅能按照流程布设理论观测形式,对野外生产中的特殊观测系统设计优化指导意义较小。笔者改变了一般的射线追踪思路,将上覆地层界面进行区间化,以目的层共反射点为目标,分段计算地震波传播路径,利用Matlab软件编程实现,克服了三种主流射线追踪方法在路径计算方面的缺点,准确确定目的层覆盖次数分布特征,查找影响覆盖次数的关键炮集,优化激发点,弥补常用设计软件的不足,指导野外生产,提升资料品质。

1 方法原理

1.1 基本思路

假设地层为均匀连续层状介质,则射线由起始点向下穿越不同的目的层经过反射,折射后到达目的层固定反射点位置,然后再经过不同地层反射、折射后回到地面的路径是可以精确计算的。当以激发点为起始时,在限定偏移距的条件下,可以计算出经过每个反射点的路径数量,得出目的层的有效覆盖次数。当以接收点为起始时,可以计算出实现目的层覆盖次数均匀条件下的所有炮点分布特征。无需限定终止点的位置,射线与地面的交点若未处于整道位置,通过微调反射点的位置即能实现交点归位,而且微调后的反射点与原反射点仍属于同一线元。

1.2 射线路径计算方法

1.2.1 单一路径的计算

以共反射点位目标的射线追踪方法将射线路径分成由起始点到反射点和由反射点到终止点两部分。将上覆地层细分成若区间,地震波的穿越不同地层每一段区间的传播路径间的相交,在地层界面上的反射和折射关系表示为多个非线性方程,计算反射、透射点的过程也就转换成非线性方程组求根的过程。Matlab中的多元非线性方程组快速求解算法、微分方法、插值算法使射线路径的计算得以快速实现。

图1为简易三层界面地震模型,v1、v2、v3为不同地层的层速度;L11-L12,L21-L22,L31-L32,L23-L24,L13-L14为不同界面上有限长度的线段区间。假设存在S到C然后到R的路径,经过L11-L12之间的P1,L21-L22之间的P2,L23-L24之间的P3,L13-L14之间的P4,那么射线路径计算方法如下:

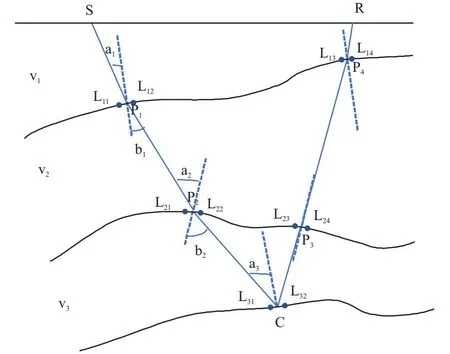
图1 炮点经CRP点到达地表的路径示意图Fig.1 Source-CRP-surface pathway diagram

1)S-C路径计算

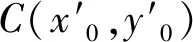
y1-y0=k11*(x1-x0)

(1)

y1-y12=k1*(x1-x12)

(2)

y2-y1=k22*(x2-x1)

(3)

y2-y22=k2*(x2-x22)

(4)

(5)

cos(tan-1k11-tan-1k1)*v2=

cos(tan-1k22-tan-1k1)*v1

(6)

cos(tan-1k22-tan-1k2)*v3=

cos(tan-1k33-tan-1k2)*v2

(7)

Matlab自带的多元非线性方程组求解函数,每次仅能计算出初始赋值附近的一个根。求得方程组根以后,需要确保P1(x1,y1)在L11-L12之间,P2(x2,y2)在L21-L22之间,以及入射路径和折射路径位于法线的两侧。针对射线路径的判断,运用向量的夹角计算公式进行推导计算,方程根需满足式8和式9。只有满足以上所有条件的根才算方程组的有效解。

(8)

(9)

2)C-R路径计算

在计算得到P2以后,可计算P2C的斜率,进而得出P3C的斜率。利用线性插值和微分方法计算出L23、L24、L13、L14的坐标,L23L24,L13L14的斜率k5,k6。计算出由反射点C到P4的路径需要建立基于P3P4斜率,P3,P4坐标的5元非线性方程组,包含过P3、P4的4个线段的斜率,满足P3处斯奈尔定律的5个方程,与S-C路径的方法类似。满足P3在L23-L24之间,P4在L13-L14之间,以及入射路径和折射路径位于法线两侧解方程的解为有效解。当地层数量为n时,方程组的元数为3n-1。得到交点P3,P4以后,进而计算出R的位置。

1.2.2 全路径的计算

多元非线性方程具有多解性的特点,但在一定的范围内,解是唯一或是不存在的。对于已知的观测系统和地质模型,计算过目的层所有线元的射线,需要将上覆地层界面以固定的区间进行划分,利用S-C,C-R的路径计算方法和循环运算,逐个判断和查找穿越所有区间的路径。假设地表物理点的个数为m,目的层CRP点为n,每层上覆地层界面数量为i,每层区间的数量为k,则循环运算的次数c满足式5。

c=m*n*k2*i

(10)

此方法不但可以计算S-C-R的路径,也可以将S替换成R计算R-C-S的路径。当所有的路径计算完成以后,根据观测系统设定限制偏移距和反射角大小后,进而统计穿越不同线元的路径数量可以得到目的层的有效覆盖次数。若不限定偏移距范围,通过S-C-R的路径计算可以得出在炮点均匀布设条件下实现较均匀采样的道集,进而指导偏移距的选择。在限定偏移距和反射角的条件下,也可以通过R-C-S逆向路径的计算,得到检波点均匀布设条件下,实现较均匀采样的炮集,指导激发点优化。

1.2.3 关键参数的设定

在射线路径的计算中,穿越目的层固定线元的最终路径的多少除受地层特征和观测系统设定影响外,还受到反射角限定和上覆地层划分区间大小的影响。

地层入射角方面,华凯等人[10]在入射角对地震动特性研究中指出随着入射角增的增大,P波作用引起的水平位移动与S波作用引起的垂直位移通常会增大,地震动轨迹构成的轮廓面积随之增大,持续时间变小。当入射角达到临界角以后,进而产生折射波等。区别于其他方法,本方法中研究人员可以根据研究需要自主限定反射角大小,满足不同的研究条件。

地层区间划分方面,类似于迭代法的网格设定,上覆地层区间设定是影响计算精度和效率的关键参数。地下地层受构造变动影响往往为弯曲的界面,但地层界面在有限的范围内可以近似表示为直线,斜率可以准确计算。范围越小,利用多段线段刻画出来的界面就越准确。随着范围增大,计算精度逐渐发生变化。同时由于MATLAB每次仅能计算出方程组的一个解,当同一区间存在多路径时会出现漏解的问题。研究人员对比分析了将目的层的上覆地层以线元(1/2道距),1/2线元,2倍线元划分,以及有限折点法(将地层按照转折点分成少量的线段)等区间划分方式,除有限折点法外,其余三种方法得出的结果一致,研究人员认为在线元或者线元大小相近的尺度上划分区间大小能够确保路径计算的完整性,避免漏解。

2 模拟验证及应用分析

2.1 模拟验证

建立图2所示的二维三层地质模型,层速度分别为2 500 m/s,2 800 m/s,3 200 m/s,理论设计方案道距为50 m,炮点距为100 m,观测系统为2 475-25-50-25-2 475。在2 475 m～7 575 m范围内共布设52炮。分别利用Tesseral Pro专业模型软件和基于共反射点的射线追踪方法进行对比分析。图3为Tesseral Pro 射线追踪模拟结果,可以看出在凹陷的两翼存在明显的“反射盲区”,无有效反射路径。图4为利用Tesseral Pro进行波动方程模拟放炮、叠加、偏移、时深转换后的深度剖面,从结果中显示在凹陷的两翼存在弱反射能量,说明这些照明强度不足,同时也说明图3显示的“反射盲区”并非真正的盲区。利用新的射线追踪方法(本次限定反射角小于临界角的前提,实际可根据研究需要进行调整),结果见图5和图6。图5显示给定的地震勘探模型无明显的盲区。图6为图5的局部放大,显示在凹陷两翼的射线路径明显减少,且存在少量线元无射线路径。基于共反射点的射线追踪方法结论与波动方程模拟结果相近。

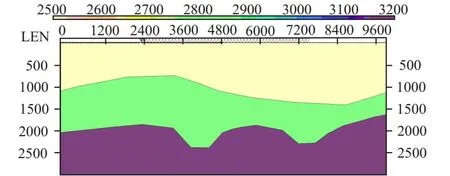
图2 二维模型Fig.2 2D model

图3 Tesseral Pro 射线追踪结果Fig.3 Ray tracing result of Tesseral Pro

图4 Tesseral Pro波动方程模拟深度剖面Fig.4 Depth section of wave equation simulation with Tesseral Pro

图5 新射线追踪方法路径计算结果Fig.5 Ray tracing result of new method

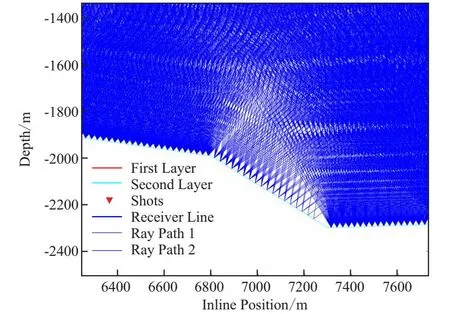
图6 新射线追踪方法路径结果(右侧凹陷左翼放大)Fig.6 Ray tracing result of new method(left wing of right sunken zooming in)

利用新方法对射线路径进行统计,得出目的层的有效覆盖次数,见图7。通过覆盖次数显示可以看出第二层左凹陷的两翼和右凹陷的左翼存在覆盖次数明显低于周边地层的问题,特别是右侧凹陷的左翼在7 287.5处覆盖次数为零,该运算结果与波动方程模拟结果基本一致,进一步验证了方法的准确性。

图7 目的层有效覆盖次数Fig.7 Effective folds of target layer(蓝线:第一层 红线:第二层)

2.2 应用分析

以共反射点为目标的二维射线追踪方法可以计算目的层的有效覆盖次数,同时可以计算基于共反射点的道集、炮集记录。实际应用中可以通过道集、炮集分析优化观测系统或激发点,实现目的层的较均匀采样。特别是针对复杂构造形态,合理的优化激发点,能够在保障目的层资料品质的前提下,最大限度地降低生产成本。

笔者将重点以利用该方法进行二维激发点优化来分析方法的应用效果。基本实现思路为通过S-C-R的路径计算反射点覆盖次数(正演),查找出问题区域、利用R-C-S的路径计算实现问题区域较均匀覆盖的炮集(反演)、优化激发点然后进行正演验证激发点优化后正演验证,具体实现流程见图8,总体技术路线和实现共分10个步骤、多次循环。

图8 激发点优化技术路线和流程Fig.8 Shots optimization technical route and flow

1)正演模拟

正演模拟主要计算在理论设计方案下,主要目的层的有效覆盖次数,从而界定需要改善的区域,改善区域主要分为三类:①低覆盖区域,需要进行加密激发;②高覆盖区域,需要进行稀疏激发;③覆盖适中区域,可根据需要加密或稀疏激发。

根据图7可以清晰看出满覆盖区域目的层反射界面的有效覆盖次数在25次左右。形态复杂的第二界面线元4 562.5～4 937.5,6 812.5～7 287.5处属于低覆盖区域;线元7 812.5～8 637.5正常应处于覆盖次数渐减带,但覆盖次数较高,两段需要通过激发点优化改善。

2)反演模拟

利用程序计算出对应的需要加密、稀疏或保持不变的炮集区域(计算的过程中限定了激发点的范围为2 025～8 075)。结果见图9,2 025～4 275段、6 875～8 075段的为低覆盖CRP炮集段,通过该区域的激发点加密能够提升有效覆盖次数。5 175～8 075段则为高覆盖CRP炮集段,通过对该区域的稀疏采样能够降低有效覆盖次数。

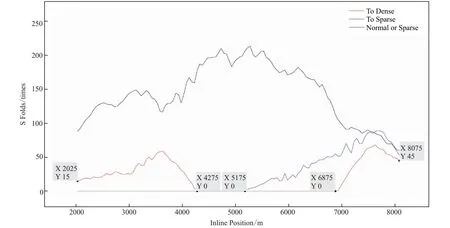
图9 实现不同目的层区域均匀覆盖的炮集分布Fig.9 Shot gather to achieve the uniform coverage of different target layer section

3)优化激发点

对反演模拟的结果进行综合分析,对所有激发点进行重新规划,在保证激发点总数变化较小的基础上,确保目的层有效覆盖次数均衡。针对图3所示的模型,在综合考虑目的层成像效果和勘探成本的基础上,确定在2 425～4 175段采用3道2炮的加密激发,4175～6875段采用3道1炮的稀疏激发,6 875～7 925段进行1道1炮加密激发的激发点优化方案,总体设计58炮,较原方案仅增加6炮。但关键低覆盖区域的覆盖次数得到较大的改善,特别是线元7 287.5处的覆盖次数由0次提升到了7次,见图10。(a:二维模型;b:第一层有效覆盖次数变化 c:第二层有效覆盖次数变化)

图10 激发点优化后不同目的层有效覆盖次数图Fig.10 Effective folds diagram of different target layers before and after shots optimization

4)效果分析

以共反射点为目标的射线追踪思路,使该方法在提升目的层成像效果方面更有针对性,也更为便捷。基于本方法的整套Matlab程序能够快速、直接地查找二维地震勘探过程中目地层的低覆盖区域,明确影响覆盖次数的关键炮点和检波点,实现物理点的精准优化,以最小的投入提升资料的品质。

3 结论

笔者改变了由激发点到接收点的射线追踪思路,提出了由激发点或接收点经过CRP点再到地表的射线路径计算方法,并利用软件编程实现自动化计算,用于指导和验证二维激发点和观测系统优化及效果分析。但本方法主要存在两方面的不足:

1)研究主要针对P波入射,P波反射和透射计算,未计算转换波、折射波等衍生地震波,解决有效覆盖的问题而无法进行波组分析。

2)本文中的方法编程实现利用了MATLAB在矩阵运算,方程求解等方面的优势,降低了编程难度。但MATLAB由于其自身基于向量的运算方式,在循环运算方面存在效率低的短板。针对图2所示的模型,完成图8的全流程计算需要1个小时。

笔者所述的方法也可以通过其他编程语言实现或是在并行计算方面进行改进,进一步提升运算效率。此方法可作为传统射线追踪方法或是波动方程模拟方法的补充,快速解决重点区域构造成像问题。在实施过程中为了设计工作者可以仅主要针对重点目的层段进行分析和优化,或者对形态单一的目的层的上覆地层进行简化处理,降低计算工作量,使运算更为便捷。