软岩巷道临时支护支架与围岩相互作用的数值模拟

宋胜伟, 刘鹏伟

(黑龙江科技大学 机械工程学院, 哈尔滨 150022)

0 引 言

近些年,国内经济的快速发展得益于能源开采规模的不断扩大,尤其我国是以煤炭作为主要的能源继而进行各种生产活动。在煤矿巷道开采过程中,巷道支护尤其是松软破碎的巷道中的支护问题日益突出,U型钢支护作为一种主要的巷道支护方式,在国内各大矿区得到广泛的应用,其具有地质适应性广、支护强度大,能使压力以适应围岩变形,安装方便、可重复使用等特点。U型钢可缩性金属支架在软岩巷道中能够有效控制并适应围岩变形[1-2]。但由于金属支架刚度小,围岩来压时金属支架易失稳,金属支架的收缩率通常不足以使其在软岩巷道中得到有效应用[3]。U型钢支架在全断面支撑巷道围岩过程中,应力集中出现在拱脚和两帮处[4-5],由于支架连接方式的不科学容易导致结构不牢固[6],改善受力不均的方式通过结构补偿实现,采用U型钢及联合其他支护技术在软岩巷道支护实际工况中取得了明显的效果[7-8]。

笔者提出采用软岩巷道临时支护支架对巷道进行支护,设计支护参数,通过数值模拟分析巷道围岩的变形与巷道稳定性。

1 临时支护支架力学模型

临时支护支架力学模型如图1所示。支架直墙部分高度为H,主支撑立柱与两肩梁铰接于j、g两点,支撑角度为θ1,辅助支撑油缸与两侧帮梁铰接于n、e两点,支撑角度为θ。

图1 支护支架受力计算模型Fig. 1 Calculation model of support bracket force

顶部弧形梁与直墙部分铰接于m、f两点处。对于在建立模型时要考虑到应力的不均匀分布,并进行适当简化,nm、mi、ih、hf、fe段对应载荷分别是F1、F2、F3、F4和F5。

1.1 求支座垂直反力

从建立的受力计算模型中分析可知,要想计算垂直反力N1、N2,需要从支架的铰接m、f点处考虑,该部分垂直反力的计算如图2所示。

图2 垂直反力计算受力分析Fig. 2 Force analysis of vertical reaction force calculation

由力平衡条件∑γ=0可知:

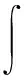
(1)

(2)

1.2 支架水平推力

支架顶梁和腿部静定状态受力如图3所示。假设的未知力为Fx,方向垂直于侧护梁,对其进行求解。

图3 支架顶梁和腿部静定状态受力Fig. 3 Statically indeterminate state force analysis of top beam and legs of support

由图3可见,支点d存在向右运动的位移u0,其基本方程为

(3)

式中:δ11——基本结构在单位力x=1单独作用下在d支点上产生的水平位移,方向向右;

Δ1P——基本结构在载荷F1、F5单独作用下d支点产生的水平位移,方向向左。

弯曲变形是导致支架破坏的主要诱因,受到的剪力、轴力对位移几乎没有影响。

2 临时支护支架工作原理

临时支护支架在工作时的三个工位状态,如图4所示。

图4 临时支护支架各工位状态Fig. 4 Status of each station of temporary support bracket

工位一为巷道掘进初期,该支架进入支护作业并以最大伸展姿态支撑巷道,降低围岩的变形速度,此时支架受力呈快速上升阶段;工位二由于软岩吸水膨胀易导致围岩发生泥化变形,应力变大,支架让压收缩,防止被挤压产生破坏;工位三是软岩巷道变形进入后期阶段,需要进行永久支护,该临时支护支架缩到最小位置以便于进行转运工作。

当巷道围岩变形压力超过支架安全阀调定压力,则支架随之进行收缩下降。当下降到一定距离则继续恒阻阶段,直至巷道围岩变化较为稳定。临时支护支架支护过程曲线如图5所示。从图5可以看出,支架在工作过程中分为四个阶段,ab段是支护刚开始,巷道周边围岩变形较为剧烈,支架依靠自身对抗围岩压力;bc段是恒阻阶段,此时围岩压力变化暂时处于相对平稳的状态;cd段围岩继续发生变形,支架继续发挥承载作用抵抗变形;de段是破坏阶段,围岩压力超过安全阀调定压力,支架失去作用。

图5 临时支护支架支护过程曲线Fig. 5 Curve of support process of temporary support bracket

3 数值模拟与结果分析

3.1 巷道模型建立

假设条件为岩体为均质体,计算尺寸长宽高为80 m×60 m×60 m。开挖后的模型网格划分如图6所示。岩石力学参数如下:弹性模量为2.1 MPa、泊松比0.4、内摩擦角65°、内聚力1.3 MPa、抗压强度20 MPa、抗拉强度1.4 MPa、抗剪强度1.7 MPa。

图6 巷道计算模型Fig. 6 Roadway calculation model

3.2 巷道围岩与支架应力位移量变化

巷道围岩垂直和水平位移分布云图,如图7和8所示。支架支护后,0.5、1.0、1.5、2.0 m四种间距下布置的支架的垂直位移量分别为1.6、1.95、2.03和1.89 mm。从图8可见,在巷道围岩的水平位移方面,0.5 m布置方式显示左侧护梁的位移量为0.76 mm,右侧护梁的位移量为0.73 mm,总移近量为1.49 mm;1.0 m布置方式显示左帮的位移量为1.14 mm,右帮的位移量为1.12 mm,总的两帮移近量为2.26 mm;1.5 m布置方式显示左帮的位移量为1.34 mm,右帮位移量为1.31 mm,总的两帮移近量为2.65 mm;2.0 m布置方式显示左帮位移量为1.41 mm,右帮位移量为1.37 mm,总的两帮移近量为2.78 mm。从围岩变形量来看,两支架间距0.5 m布置,对于控制软岩巷道在水平和垂直方向上的位移具有明显的效果。

图7 巷道围岩垂直位移分布对比云图Fig. 7 Contrast cloud map of vertical displacement distribution of surrounding rock of roadway

图8 巷道围岩水平位移分布对比云图Fig. 8 Contrast cloud map of horizontal displacement distribution of surrounding rock of roadway

支架的应力变化如图9所示。支架上各点在围岩变形期间的应力变化如图10所示。由图10可见,支架各个部位在巷道掘进过程中的应力变化规律,在巷道变形初期,围岩变形较大,所导致的应力也相对较大,则支架的应力最大值出现在了右拱肩处,达到了409 kN。这是由于巷道右侧的围岩相较于左侧围岩的接触应力较大,进而随着围岩变形不断向外扩张,这些压力就到了支架上,所以导致支架各部分的受力不均,且应力变化比较大,容易造成支架的破坏。随着巷道继续往前掘进到40 m时,支架已经对围岩支撑了一段时间,随着时间的推移,巷道围岩应力也随之下降,支架的应力也呈现出不同程度的下降趋势,左拱肩处从222 kN下降到200 kN,拱顶处从267 kN下降到240 kN,此时支架应力的变化较为平缓。当巷道掘进到60 m时,巷道围岩进入蠕变阶段,除此时支架各处的应力较为稳定,没有发生大的变化。当掘进到80 m时,围岩应力再平衡已形成,对于支架而言,应力保持在比较稳定的状态,右侧帮处的应力基本维持在268 kN。

图9 支架各状态应力图Fig. 9 Stress diagram of bracket in each state

通过设置主支撑立柱和辅助支撑油缸的具体数值,得出支架的各零部件运动规律。设置主支撑立柱作用力为200 kN,辅助支撑油缸作用力为150 kN。经过模拟结果可得,各铰接点在支架下降的过程中力的变化曲线如图11～14所示。

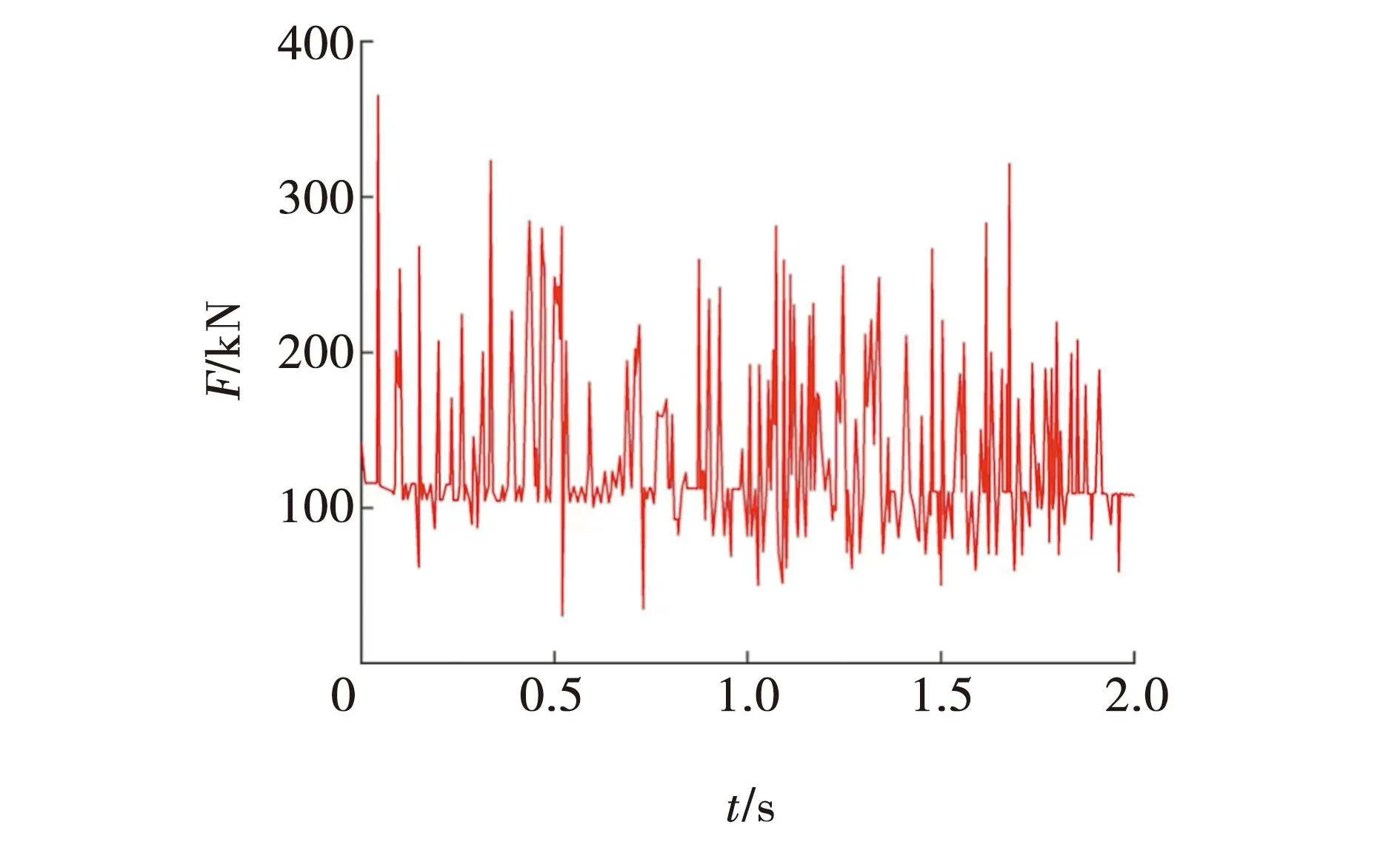
图11 辅助支撑油缸与左侧帮铰接点受力Fig. 11 Force of hinge point between auxiliary support cylinder and left side

图12 主支撑油缸与右肩梁铰接点受力Fig. 12 Force of hinge point between main support cylinder and right shoulder beam

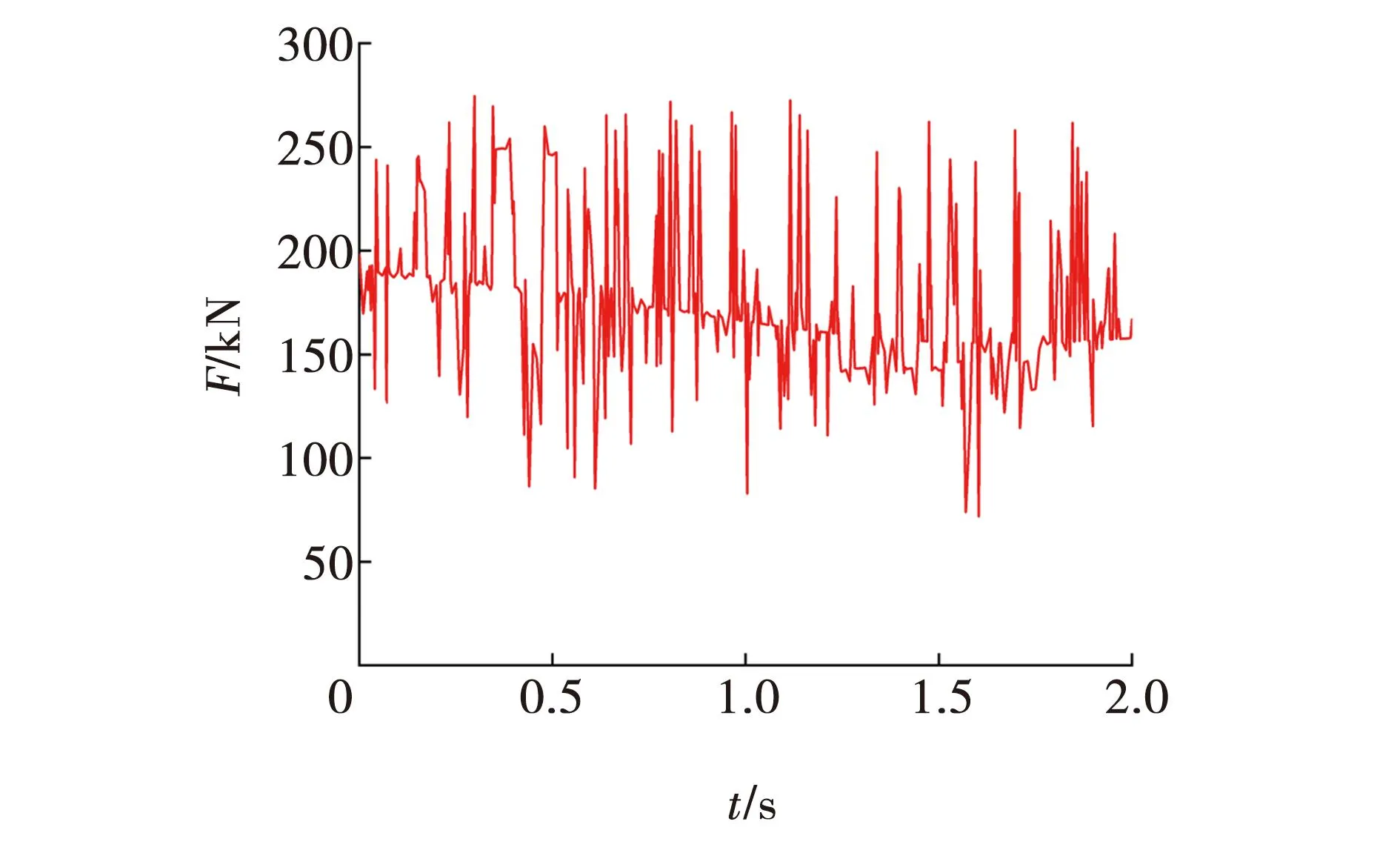
图13 主支撑油缸与左肩梁铰接点受力Fig. 13 Force of thinge point between main support cylinder and left shoulder beam

图14 辅助支撑油缸与右侧帮铰接点受力Fig. 14 Force of hinge point between auxiliary support cylinder and right side

对主支撑油缸和辅助支撑油缸施加作用力分别为200和150 kN时,得到了油缸和肩梁、两侧帮处的铰接点力的变化。在整个运动过程中,支架的整体受力范围大小趋于稳定,总体处于100～350 kN之间。从图11可以看出,辅助油缸与左侧帮铰接点处的载荷最大达到了370 kN,在此过程中该处合力的变化呈现出一定的规律性。从图12可以看出,主支撑油缸与右肩梁铰接点处的载荷达到375 kN,总体上呈现下降的趋势,这是由于支架达到了安全阀调定压力,一旦围岩压力过大超过支架所能承载的范围,溢流阀打开,支架随之下降。由图13可见,为主支撑油缸与左肩梁铰接点处合力的变化,其变化规律与右肩梁处大致相同。由图14可见,辅助油缸与右侧帮处铰接点处的合力变化,大小基本维持在180 kN上下。

4 结 论

(1)采用该支架支护后,a、b、c、d四种间距下布置支架的垂直位移量分别为16.08、19.51、20.3和18.89 mm。

(2)巷道变形初期,支架的应力最大值出现在了右拱肩处达到409 kN,说明支架右侧受到的破坏较大。随着掘进深度往前推进,左拱肩处从222 kN下降到200 kN,拱顶处从267 kN下降到240 kN,变化较为平缓直至围岩应力再平衡。

(3)对支架进行动力学仿真分析得到,在支架受力下降过程中,支架右半部分所受的力明显大于左半部分,表明围岩在变形过程中并不是呈现均匀变化的,容易使支架受到集中力的破坏。