盐冻作用下水泥路面毛细吸水系数演化及应力状态分析

董连成, 金圣豪, 王金玉

(黑龙江科技大学 建筑工程学院, 哈尔滨 150022)

0 引 言

水分传输既是外部有害离子进入混凝土内部的重要媒介,也是混凝土结构发生耐久性破坏的重要原因[1]。对于实际工况下的水泥路面而言,材料处于非饱和状态,此时路面的吸水作用主要受毛细吸力影响。

针对混凝土材料毛细吸水作用的效果与机理,国内外专家学者做了大量的研究。文献[2-4]分析了材料本身在不同初始条件下,对混凝土毛细吸水能力的影响,并明确分析了各要素的影响程度。梁建国等[5]对多孔性混凝土砌块进行了冻融后毛细吸水试验,结合毛细吸水动力学理论分析了不同孔径混凝土的毛细吸水规律,得出了影响多孔性混凝土砌块冻融破坏的毛细吸水系数。梁晓前等[6]对蒸汽加压混凝土与普通混凝土分别进行了冻融循环及毛细吸水试验,结合数据分析与微观手段证明毛细吸水系数随着孔数量的增加而增大。蒋科等[7]通过试验的手段对比了不同盐冻条件对混凝土孔隙率及孔隙分布的影响,结合孔结构分形维数对混凝土的孔结构演化做出来定量分析。上述研究成果证明了混凝土毛细孔吸水系数可以作为一项抗冻性能指标,但当前对于毛细吸水系数与其他抗冻指标之间的关系需要进一步研究。同时对于在役期的连续配筋混凝土路面与水泥路面而言,实际工况中会经历一个湿润后干燥的过程[8],当前而言仅对湿润阶段的毛细孔吸水系数进行了初步探索,并未考虑盐冻损伤对水泥路面内部湿度分布及应力状态的影响。

故针对上述情况,笔者通过室内盐冻试验及冻后混凝土毛细吸水试验,获取了不同盐冻环境下的混凝土毛细孔吸水系数。结合冻后混凝土力学性能测试探究混凝土冻融损伤演化规律,以建立冻融损伤指标与毛细孔吸水系数的联系。依据试验数据结合有限差分法(Finite difference method)与有限单元法(Finite element method)对高寒季冻区在役期的CRCP及CCP路用性能控制给出建议。

1 计算理论

1.1 水分迁移理论

对于在役期的水泥路面而言,水化过程早已完成,此时忽略自干燥对路面内部湿度的影响,则菲克定律可以写成:

(1)

式中:H——相对湿度,%;

D(H)——湿度扩散系数;

t——时间。

对于湿润过程及干燥过程而言,均可采用式(1)进行描述,不同之处仅在于湿度扩散系数D(H)的不同,对于干燥阶段湿度扩散系数可表示为

式中:D1——饱和状态下的扩散系数;

α0、Hc、n——依据文献[8]取经验值,分别为0.025、0.792、6。

湿润阶段湿度扩散系数则可表示为

D(θ)=D0emθ,

式中:D0——完全干燥时的扩散系数,可由混凝土毛细吸水试验获得,亦是本文的研究重点;

m——经验系数,文中取6[8-10]。

两者之间用于表述湿度扩散的指标并不相同,故可以通过BSB模型[8]进行转换。

(2)

式中,C、k——环境相关系数,主要由外部湿度边界决定。

1.2 数值分析理论

水分在水泥路面内部的迁移过程为非线性扩散方程,常规计算手段难以获得解析解。考虑到有限差分法(FDM)在解决流体瞬态问题上有绝对优势,故利用Matlab结合FDM数值计算手段计算水泥路面内部湿度梯度。

对式(1)进行时间域向前差分,空间域向后差分,此时即可得到对应的离散方程为

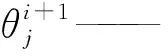
x——空间步长。

文中所述过程的湿度扩散方程为

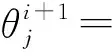
1.3 等效非线性温度梯度转换

当前对于路面内部湿度梯度所产生的翘曲应力研究,通常将不成熟的湿度梯度转换成更为成熟的温度梯度进行研究。刘晓光[9]提出了可以将温度梯度与湿度梯度间产生的收缩变形进行等效,从而实现温湿度梯度的转换,转换公式为

(3)

式中:α——热膨胀系数;

φA——混凝土中骨料的体积分数;

n——骨料引起的收缩限制系数,取1.68[10];

H(t,z)——t时刻距中性平面距离为z处混凝土的相对湿度。

基于式(3)即可实现相对湿度梯度与非线性温度梯度之间的转换,同时结合有限单元法(FEM)法便可实现,盐冻损伤导致的水泥路面内部湿度变化引起的湿度翘曲应力变化。

2 损伤混凝土毛细吸水试验

2.1 原材料及配合比

采用PO42.5普通硅酸盐水泥,粗骨料为级配碎石,细骨料为中砂。矿物掺料为一级粉煤灰,外加剂采用聚羧酸减水剂,混凝土配合比见表1。

表1 水泥路面配合比

试验采用的混凝土水灰比为0.4,粉煤灰掺量为25%,砂率40%,满足寒区水泥路面建设要求。

2.2 试样制作及养护

为严格控制龄期及后续各项试验环境变量,此处采用一批100 mm×100 mm×100 mm的试样开展盐冻试验。依次对冻后混凝土进行毛细吸水测试、相对弹性模量测试及立方体抗压强度测试。将表1所示砂、石、水泥、粉煤灰等干料按比例倒入强制式搅拌机中,使得干料搅拌均匀。加入90%左右的水进行湿拌30 s,然后,将剩余的水及减水剂倒入,维持搅拌1 min。将拌合料一次性装入事先涂抹脱模剂的ABS试模之中。试模放置于振捣台上成型,1 d后进行拆模。最后,将试件送入标准养护箱内养护,养护期为28 d。

图1 试样制备及养护过程Fig. 1 Preparation and curing of samples

2.3 盐冻机制选择及毛细孔吸水系数测试

当前对于混凝土盐冻试验尚未有统一的标准,考虑到实际工程中的水泥路面饱水程度较高,单面冻结法采用的试样内部较为干燥,与实际不符[11],故此采用饱水冻融结合美国ASTM推荐方法中的Plan B开展混凝土试件盐冻试验。当前市场上的除冰盐大多为氯盐,故此配置3%及5%的浓度的NaCl溶液作为侵蚀溶液,同时设置清水对照组。不同地区所遭受的盐冻程度也不尽相同,同济大学的姚祖康教授[12]曾针对这点做了研究,图2为我国北方代表性城市一年内冻融循环次数。

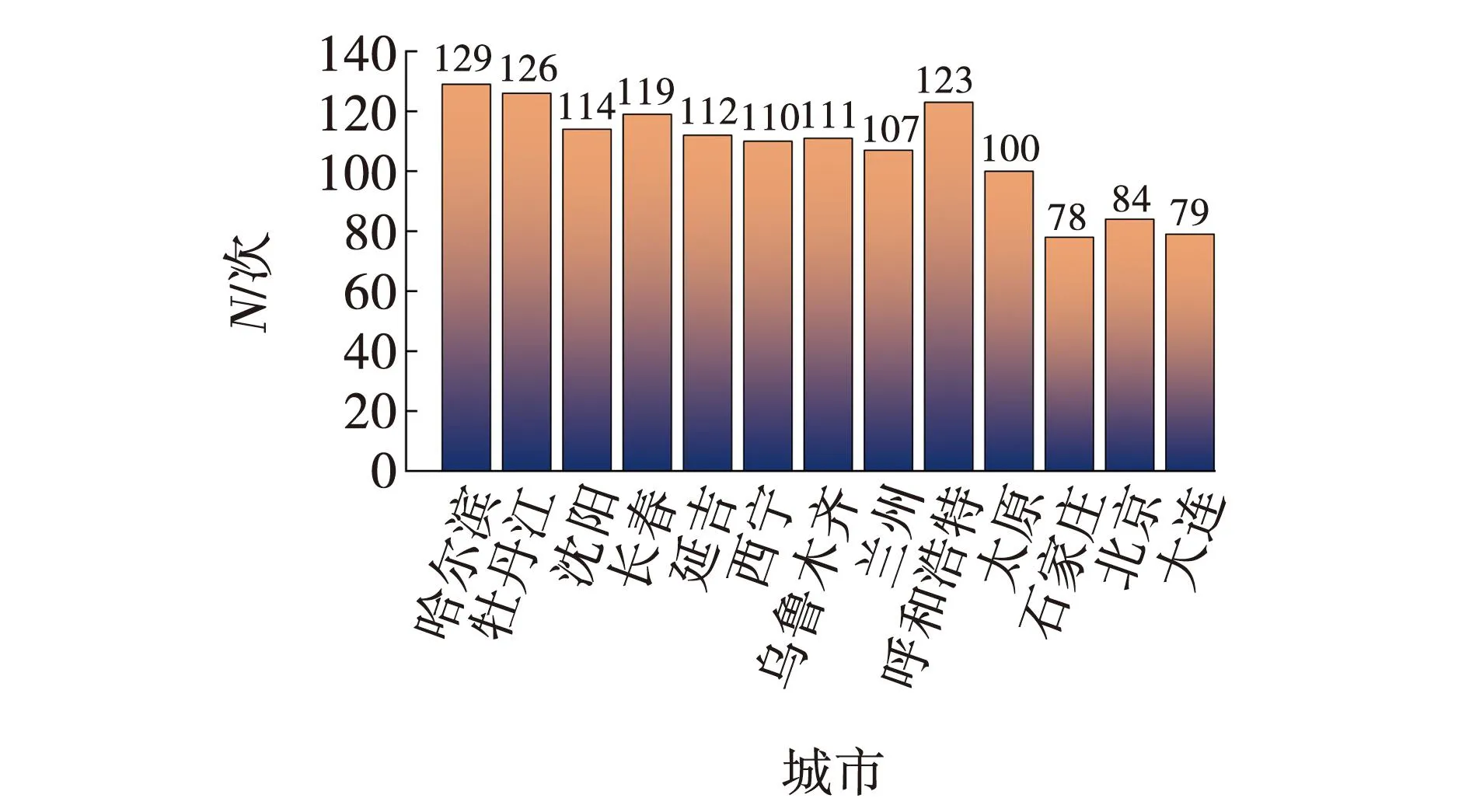
图2 北方代表性城市冻融循环次数Fig. 2 Number of freeze-thaw cycles in representative northern cities

由图2可知,北方代表性城市经受的冻融循环次数平均值约为110次,考虑到规范以25次为周期进行测试,故此取一年冻融次数为100次进行盐冻试验。进行试验时,将试样在侵蚀溶液中浸4 d(图3a),将试样放置冻融循环箱(图3b)内以低温-17 ℃、高温6 ℃进行冻融循环试验。

图3 试件饱和过程及冻融设备Fig. 3 Specimen saturation process and freeze-thaw equipment

为了降低静水压力的影响,采取上吸法进行受冻后混凝土试样的毛细吸水试验。将盐冻完成的试样送入烘箱中烘干36 h,此后以2 h为一个周期将试样取出并称重,当试样连续3次称重质量未发生变化时,代表试样内部可蒸发的水分为0。为保证一维扩散,以树脂封闭试样的上表面及侧面,留出接触面与水接触,对封闭完成的试样进行称重记录为M0。毛细吸水示意图见图4。

依据图4的方式开展毛细吸水试验,试验过程保持接触面在水中1～5 mm。混凝土的毛细吸水过程均可分为两个阶段,即线性上升段与平稳段。在线性上升段时,毛细孔吸水能力是其主要作用,随着吸水质量的增加,毛细孔吸水能力与重力等其他因素达到平衡态时,混凝土吸水开始变得困难。故此整个试验的时间为11 h,同时将吸水过程分为0～3 h、3～11 h两个阶段。两个阶段的测试间隔分别为0.5、2 h,每个间隔点进行称重测试,在时刻t测得的质量记为Mc(t),结果见图5。

图4 毛细吸水示意Fig. 4 Capillary water absorption

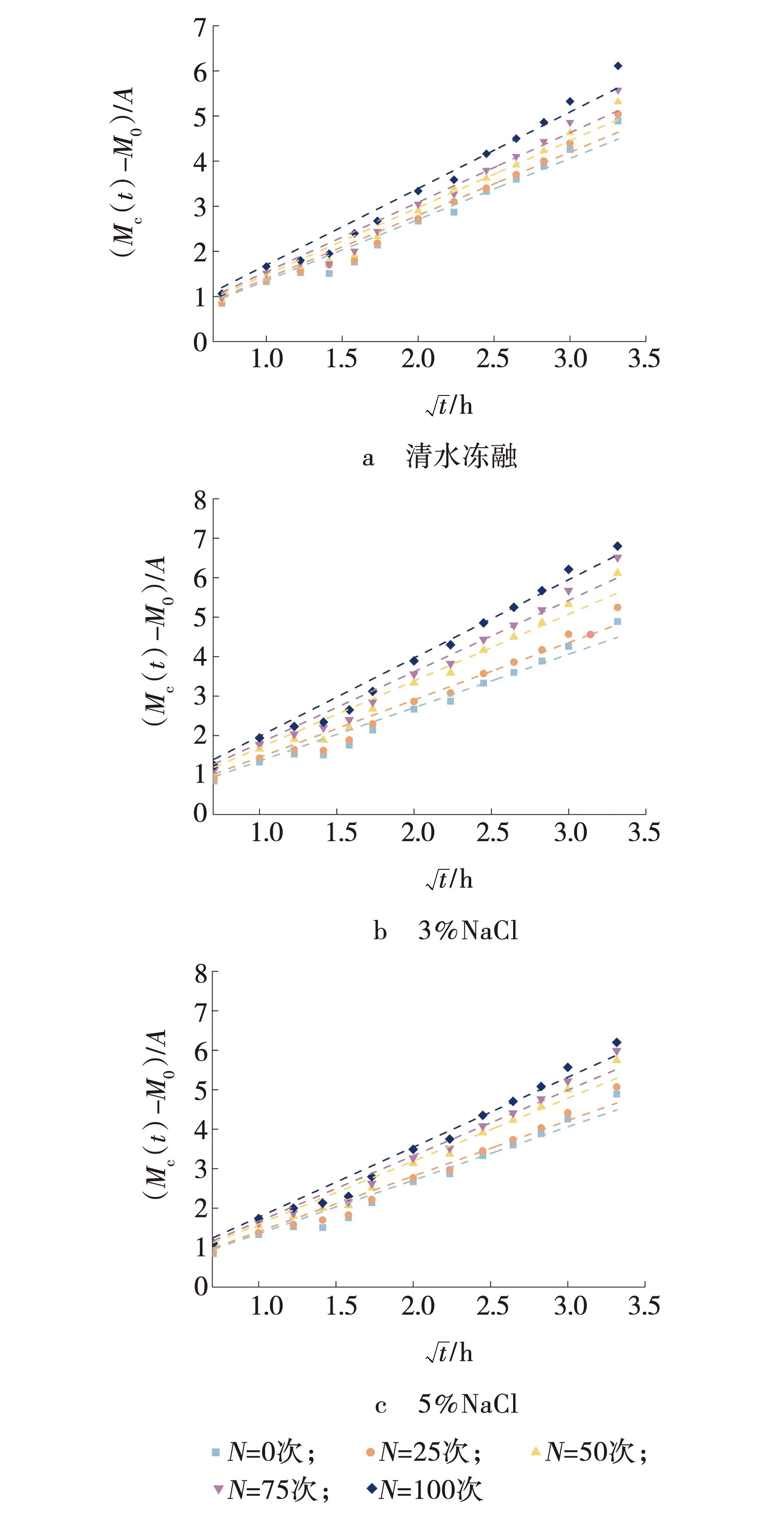
图5 毛细吸水试验结果Fig. 5 Results of capillary water absorption test

在宏观表现上,混凝土材料单位面积的吸水量可以表示为

(4)

式中:M——混凝土的吸水质量;

A——接触面面积;

S——混凝土毛细孔吸水系数。

通过对图5的试验数据结合式(4)进行回归分析,即可获得不同浓度盐溶液,不同盐冻次数的混凝土试块毛细孔吸水系数。

2.4 盐冻损伤模型的建立

为了建立针对混凝土随盐冻次数发展的损伤模型,此处对毛细吸水后的试件进行烘干处理依次测定其相对动弹性模量后,进行抗压强度测试。

相对弹性模量测试采用的50 kHz的发射及接收探头进行P波波速测试,当试验试样最小尺寸大于声波波长时,相对弹性模量可表示为

(5)

式中:ρ——混凝土材料的密度;

ν——泊松比;

v——P波波速。

对于本文采用的OCC(普通混凝土)而言,内部波速大致范围介于3 800～4 200 m/s之间,采样频率为50 kHz时,波长范围约为76～84 mm,文中采用的立方体试块最小尺寸为100 mm。采用式(5)进行计算是合理的。

立方体加载所用设备为WEP-1000屏显万能试验机,加载速率取0.5 MPa/s。为了探寻合理的损伤度评价指标,利用式(6)、(7)对抗压强度和相对弹性模量计算结果进行处理。

(6)

式中:E0——未经受盐冻损伤时动弹性模量;

EN——盐冻循环N次时的动弹性模量。

(7)

式中:fc0——未损伤前的立方体抗压强度;

fcN——冻融N次以后的立方体抗压强度。

试验处理结果见图6。由图6可知,无论是由相对弹性模量或是抗压强度对混凝土损伤程度进行表征,混凝土随盐冻次数的增加损伤程度均不断增大,在采用相对弹性模量进行损伤度表征时得到的结果更为直观。随着盐溶液浓度增大,侵蚀溶液对混凝土的损伤程度呈现先增后减的趋势。原因在于高浓度的溶液冰点低,内部液体的过冷水状态减缓了盐冻作用地带来的损伤。

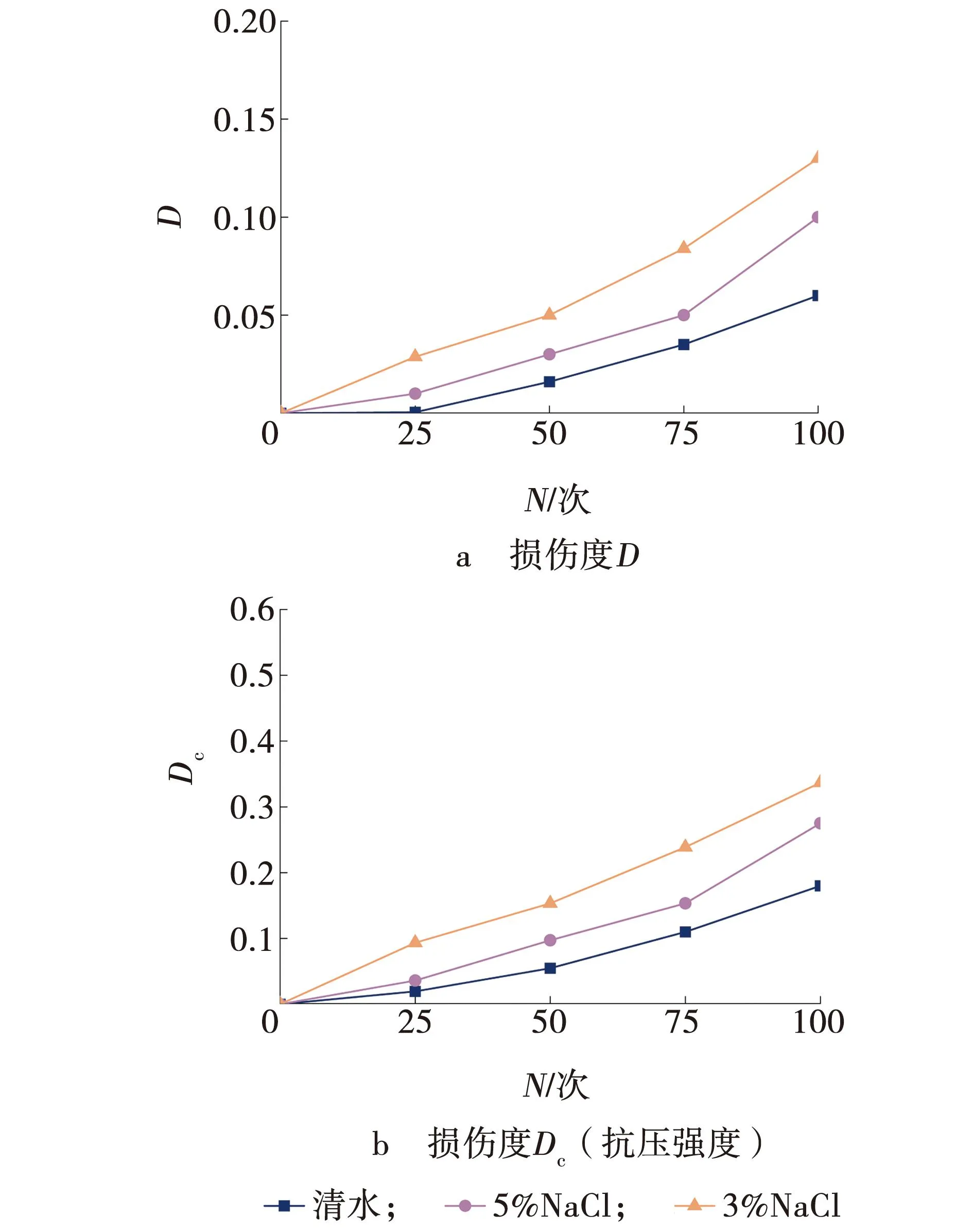
图6 混凝土损伤度与盐冻次数的关系Fig. 6 Relationship between concrete damage degree and number of salt-freezing

针对混凝土的损伤演化规律,文中采用单段冻融模型进行验证,当前常用的单段冻融模型分为指数型及二次型[13-15]。各模型回归参数结果见表2。

D1=1-α·eλN,

D2=-(β·N2+γN),

式中,α、λ、β、γ——回归参数。

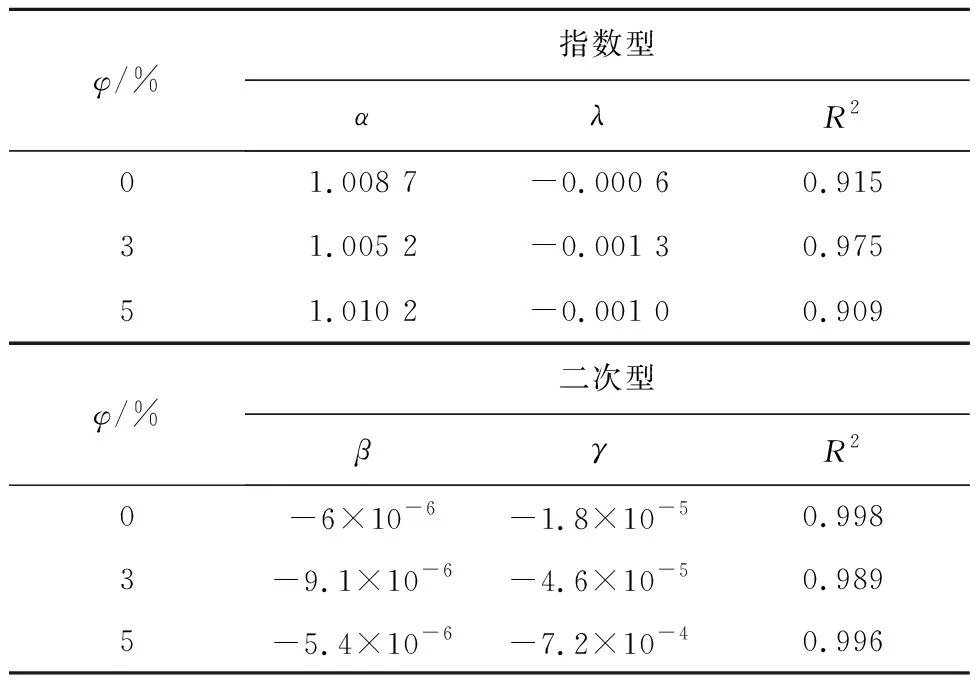
表2 单段式冻融损伤模型回归结果

由表2的回归结果可知,相较于指数型损伤单段冻融二次型模型的回归精度更高,均在0.98以上,故采用二次型损伤演化模型的结果更为可靠。

3 毛细孔吸水系数与损伤度的关联

3.1 冻融循环次数表征

为探求冻融指标与水泥路面毛细孔吸水系数的关系,此处以式(3)对图5所示毛细吸水试验结果的上升段进行回归,绘制N-S关系曲线,如图7所示。

图7 毛细吸水系数与冻融循环的关系Fig. 7 Relationship between capillary water absorption coefficient and freeze-thaw cycle

由图7可知,毛细孔吸水系数与冻融循环次数之间存在较强的非线性关系,此种关系可表示为

S=αeβN。

对三种侵蚀溶液下的混凝土毛细吸水系数进行回归,回归精度均在0.95以上,效果良好。

3.2 损伤度表征

为探求损伤度与毛细孔吸水系数间的联系,基于表2的损伤度衰减模型结合图5试验结果,绘制D-S的关系曲线见图8。

图8 毛细吸水系数与损伤度的关系Fig. 8 Relationship between capillary water absorption coefficient and damage

混凝土毛细孔吸水系数S与损伤度D之间的关系可表示为

S=eα(βD2+γD+η)。

(8)

利用式(8)对图8的结果进行回归,获得的回归系数α、β、γ、η分别为0.5、-0.41、1.82、0.24。回归精度R2为0.923,效果较好。

综上,两种表征方法均具备较高的精度,证明了毛细孔吸水系数与冻融循环次数及混凝土损伤度之间有较强的关联性,以毛细吸水系数作为抗冻控制指标是完全可行的。相较于以冻融循环次数来表征混凝土毛细孔吸水系数,损伤度的表征结果更为离散,回归精度也相对较低。但是该表征方法克服了以冻融系数表述时需分组进行的缺点,在精度要求相对较低时,具有更为广泛的适用性。

4 案例分析

为了探索盐冻损伤前后在役期水泥路面内部湿度梯度的变化,此处结合lockington公式,将损伤前及损伤度0.13时的毛细孔吸水系数转换为湿度扩散系数D0,lockington公式具体为

式中:S——毛细吸水系数,由前文所述试验获得;

n——经验系数,文中取6[8]。

4.1 损伤前后湿度梯度的变化

为了方便进行定量分析,损伤前后的计算方法一致,仅改变湿润解阶段的湿度扩散系数D0。湿润段的计算时长为72 h,总时长取28 d,两个工况干燥段扩散系数均取8×10-10m2/s,以湿润段计算结果的终点作为干燥阶段的起点。考虑到黑龙江省,各月平均最低湿度可达到40%以下,此处考虑极端情况取30%。干燥阶段及湿润阶段的转换可参照式(2),当外部湿度为30%,式(2)中的C与k可分别取18.15及0.463 5。以1.2的计算思路进行FDM数值计算。28 d后两种工况沿高度分布的湿度梯度H见图9。

由图9可知,随着盐冻进程的进行,混凝土毛细孔吸水系数不断增大,此时导致湿润阶段的扩散系数D0不断增大。外部湿润阶段对混凝土内部的影响深度不断加深,当进入干燥状态时,外部干燥对内部相对湿度的作用逐渐减弱,在表层达到干燥阶段时,中间层仍处于水分扩散阶段,导致、在役期路面出现中间湿度大,两边湿度低的情况。损伤度的累计扩大了湿润段对干燥段的影响,加剧中间段的湿度梯度突变,同时扩大了外部湿度的影响深度,当损伤度D达到0.13时,影响深度增加了接近20%。对于连续配筋混凝土路面(CRCP)而言,需重视该变化带来的钢筋锈蚀影响,而对于水泥路面(CCP)而言则需对该变化导致的湿度翘曲应力变化做进一步研究。

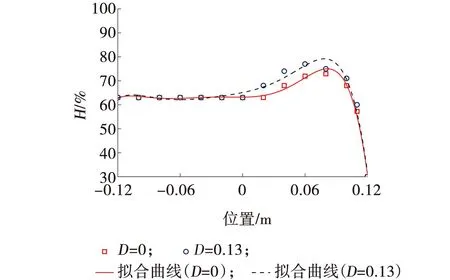
图9 损伤前后混凝土内部湿度梯度相对湿度分布Fig. 9 Relative humidity gradient distribution inside concrete before and after damage

故此时利用图9计算结果,结合式(3)以获取等效非线性温度梯度,结合FEM(有限单元法)深入探讨由损伤度引起的湿度变化对水泥路面湿度翘曲应力的影响。上述工况代入式(3)后的结果可由四次多项式进行表征,两种工况的拟合公式分别为

T0(z)=-145 928.7z4-11 253.2z3+ 1 524.8z2+103.3z-2.162,

T0(z)=-169 832.9z4-13 388.7z3+ 1 831.3z2+132.9z-1.832。

4.2 FEM模型建立

以文克勒地基上的单板模型进行计算,考虑到路面形状较为规则,此时可采用C3D20单元以获取更高的计算精度,板体模型及网格划分见图10。路面尺寸为4 m×4.5 m。

图10 路面板模型及网格划分Fig. 10 Pavement panel model and meshing

以分离式路面假设进行接触设置,即层间光滑,设置面层可从基层分离,面层基层之间设置“Hard contact”。文克勒地基则采用“Elastic foundation”进行设置,路基反应模量取110 kPa。面层及基层的模型计算参数见表3。为了控制变量此处假定面层弹性模量不变。其中,h为模型厚度、E1为弹性模量、ν1为泊松比、ρ1为密度、α1为线膨胀系数。

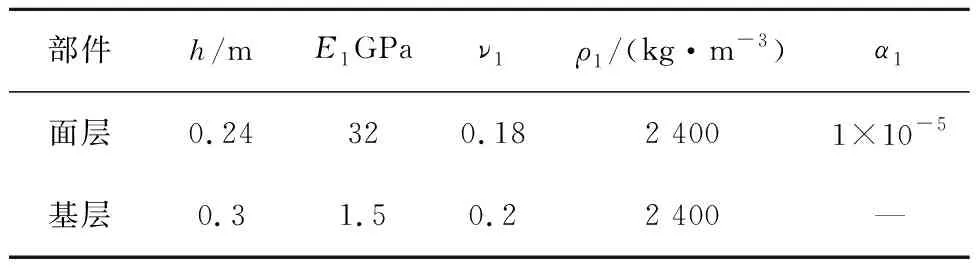
表3 FEM模型参数设置

4.3 湿度翘曲应力分析

考虑本文FEM计算过程中,应力场及位移场对温度场几乎没有影响。故此可采用顺序热力耦合的方式进行翘曲应力计算。上述两种工况在长边方向上的最大拉应力σxmax、短边方向上的最大拉应力σymax及最大湿度翘曲位移δ计算结果见图11。

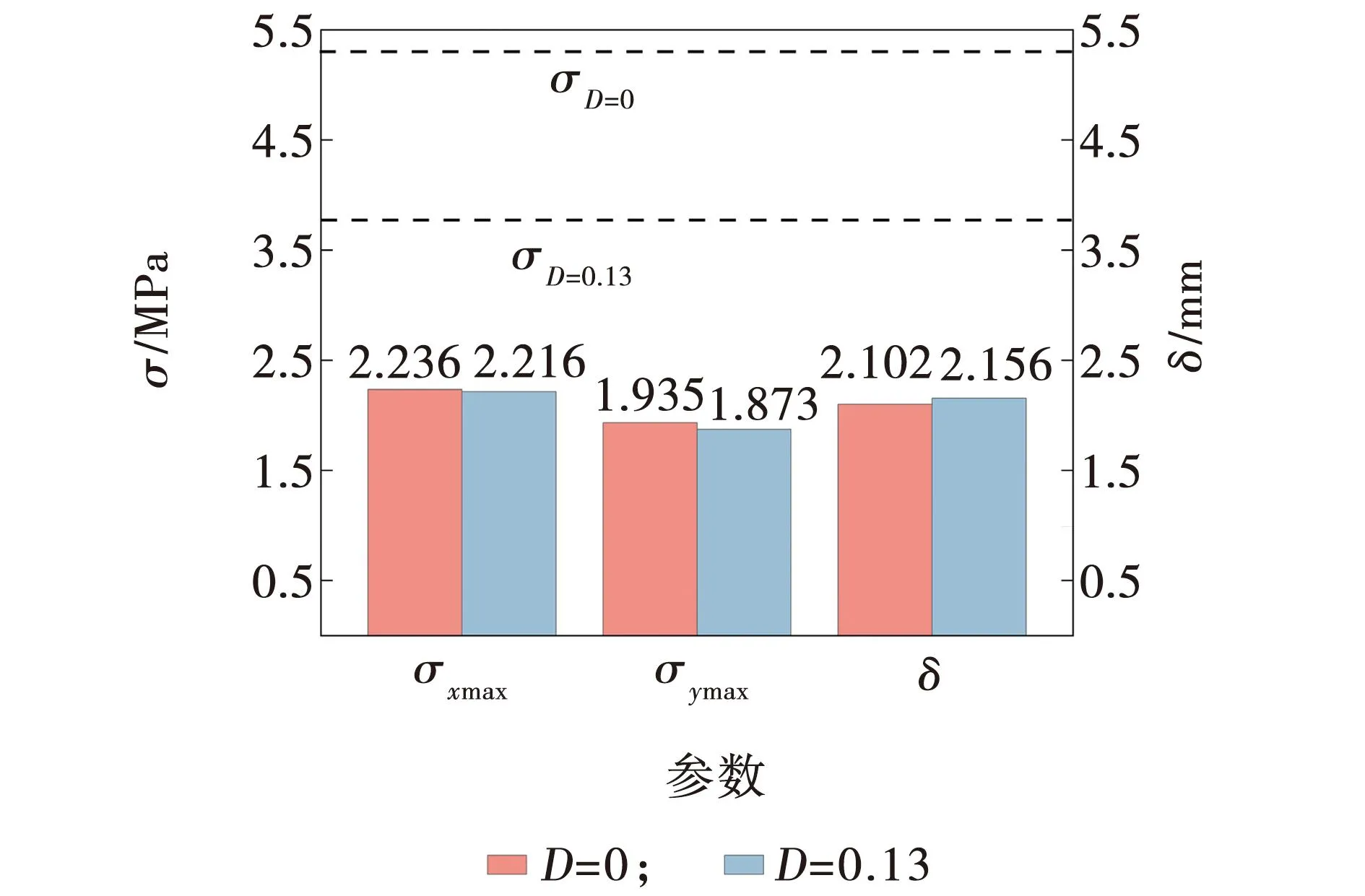
图11 损伤前后混凝土翘曲应力及位移结果Fig. 11 Results of humidity warping stress and displacement of CCP before and after damage

由图11可知,随损伤度的加大,水泥路面由湿度梯度控制的湿度翘曲应力在长边方向及短边方向上均呈现减小的趋势。然而相较于混凝土自身抗弯拉强度(可由试验数据依据文献[16]进行转换)的降低,翘曲应力的衰减微乎其微。湿度翘曲位移虽然在增大,但是在100次室内盐冻后增幅仅为2.6%。故对高寒季冻区的CCP而言,可以忽略由损伤度带来的外部湿度变化所引起的湿度翘曲应力变化,重心可转移到路面性能衰减上。

5 结 论

(1)道面混凝土在盐冻环境下的损伤演化,可以近似采用二次多项式及指数形式描述。以相对弹性模量表征的单段冻融一元二次损伤模型拟合精度均在0.98以上,相较于抗压强度,该结果更为可靠。

(2) 无论是冻融循环次数还是冻融损伤度均能较好地表征道面混凝土盐冻条件下的毛细吸水系数演化,两者的回归精度均在0.9以上。相较于冻融次数,以损伤度进行表征克服了需分组表征的不足,具有更广的适用性。

(3)当D达到0.13,混凝土路面板内部湿度影响范围增大20%,湿度翘曲应力的增幅仅为2.6%。说明对于地处高寒季冻区的CRCP需注意盐冻损伤带来湿度扩散加剧所导致的有害离子对钢筋的腐蚀。对CCP而言则可忽视该方面的影响,着重研究路面的力学性能。