基于GNSS/UWB的多无人机协同定位技术

鄢家鑫,贺晓华,周泽波,林国泉

(1. 电子科技大学航空航天学院,四川 成都 611731;2. 中国空空导弹研究院,河南 洛阳 471009; 3.航空制导武器航空科技重点实验室,河南 洛阳 471009)

0 引言

与单无人机作业相比,多无人机协同作业能完成许多更加复杂的任务,因而具有更高的应用价值[1]。在多无人机协同作业的应用中,对于无人机的导航精度有着较高的要求,而位置信息作为无人机实现导航控制所必需的关键信息,其精度对于多无人机进行协同作业而言就显得十分重要。在多无人机系统中,除了无人机自身的传感器信息外,还可以利用相邻无人机的信息辅助自身进行导航[3],这种导航方式称为协同导航。

协同导航通过利用相邻节点的观测信息与自身的观测信息进行融合以达到增强自身定位性能的目的[5],因此其本质还是多元数据融合。从其核心算法的角度分类,大致可以分为基于优化理论[7]、基于概率图模型[8]以及基于滤波估计[9]的三大类协同导航算法[10]。文献[11]通过节点之间共享卫星伪距观测信息、节点间相对位置信息以及节点自身的位置估计信息,采用最小二乘法进行融合估计以实现协同定位;然而文中将所有数据集中处理进行全局的联合估计,因此是一个集中式的结构,另外该方法忽略了观测值的方差信息。文献[12]中采用基于联合树的方法实现了卫星之间的协同定轨,联合树推理算法属于贝叶斯网络中的精确推理算法,其采用树结构对网络进行建模,然后根据消息传递算法求取各变量的边缘概率。文献[13]提出了一种基于粒子滤波器的新型混合全球导航卫星系统(global navigation satellite system,GNSS)地面定位算法,称之为混合协同粒子滤波器,该算法融合了来自卫星和地面接收器的测距数据,它是完全分布式的,并且可以提高定位的可用性和准确性;然而粒子滤波计算量较大限制了它的实际应用场景。

本文提出了一种基于GNSS/UWB的多无人机协同定位技术,超宽带技术(ultra wide band,UWB)作为一种具备高精度、低成本、体积小等特点的距离测量传感器,十分适合作为无人机之间高精度的相互观测传感器[15]。将UWB测距信息与GNSS信息融合进行协同导航,可以有效解决传统单体导航中存在的问题。

1 消息传递算法与迭代滤波

1.1 因子图与消息传递算法

对于处理多变量的复杂全局函数问题,通常可以利用因式分解的方式将其分解为若干个更简单的局部函数的乘积形式。假设一个多变量全局函数g(x1,…,xn)可以被因式分解为几个局部函数的乘积形式:

(1)

式中:J表示局部函数的集合,Xj表示全局变量{x1,…,xn}的子集,fj(Xj)表示以Xj为变量的局部函数。

在因子图中,每个变量xj都有唯一的变量节点与之对应,每个局部函数fj都有唯一的因子节点与之对应,并且使用边连接与之相关联的变量节点。以一个简单的因子图为例,在图中,空心圆“”表示变量节点,实心方块“”表示因子节点。令g(x1,x2,x3,x4,x5)表示一个含5变量的函数,并假设g可以表示为5个因子的乘积,其表达式如下:

g(x1,x2,x3,x4,x5)=
fA(x1)fB(x2)fC(x1,x2,x3)fD(x3,x4)fE(x3,x5)。

(2)

式(2)对应的因子图如图1所示。

图1 式(2)的因子图表示Fig.1 Factor graph representation of equation(2)

可以通过因式分解和分布律来计算每一个边缘密度函数。以g1(x1)为例:

(3)

式中:～{xi}表示不包括xi的变量集合。

但是在计算所有的边缘函数时会存在大量的子问题被重复计算,计算效率不高。通过和积算法用消息来表示各种计算中的子问题,将边缘密度函数的计算过程看作是消息传递的过程,建立了一种直观高效的计算边缘密度的方法。

如图2所示,μx→f(x)表示由变量节点x发往因子节点f的消息,μf→x(x)表示由因子节点f发往变量节点x的消息,n(v)表示节点v邻居的集合。

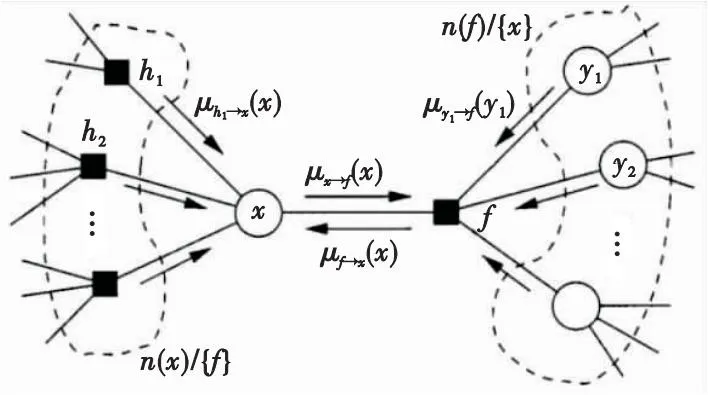
图2 和积算法Fig.2 Sum-product algorithm

和积算法中两种消息的计算由式(4)、式(5)表示。

变量到局部因子的消息:

(4)

局部因子到变量的消息:

(5)

式中:n(x)/{f}表示变量x除去f之外的邻居因子节点的集合,n(f)/{x}表示因子节点f除去x之外的邻居变量节点的集合,～{x}表示除x之外所有变量的集合,f(X)为局部函数,X=n(f)表示局部函数中自变量的集合。边缘密度函数为

(6)

1.2 迭代滤波算法

对于非线性问题,通常情况下EKF只保留到一阶项。因此不可避免地会损失精度,若使用当前时刻滤波估计的结果作为新的展开点,再次对系统进行近似展开,并再次进行滤波估计,则有助于提高估计的精度。

首先,按EKF方法进行预滤波,此时无需对均方误差矩阵进行测量更新

(7)

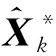
(8)

使用平滑值对一步状态预测进行修正:

(9)

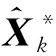
(10)

于是,可以得到迭代滤波的公式:

(11)

若迭代前后的差值小于阈值则认为迭代收敛,并输出当前结果。其流程如图3所示。

2 基于消息传递的多无人机协同位置估计

2.1 多无人机协同定位模型

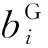
(12)

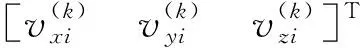
无人机i在k时刻对GPS卫星的伪距方程可表示为

(13)

无人机i在k时刻对BDS卫星的伪距方程可表示为

(14)

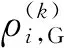
除此之外,无人机还与邻居无人机之间具备相对距离观测的能力,它们之间的距离观测方程可表示为

(15)

于是,无人机群体在k时刻的定位问题可以描述为在给定所有可用观测值条件下的后验概率:

(16)

假设无人机之间的状态相互独立,且观测值之间也相互独立,则可以根据齐次马尔可夫假设以及观测独立假设得到

(17)

(18)

对式(16)进行因式分解。为了简化书写,以下 和ρM,B统一用ρM表示,其分解过程如下:

(19)

式中:

(20)

将式(20)代入式(19)有

(21)

(22)

至此,已经得出全局概率密度的因式分解形式,若要求解无人机i的边缘密度,则需对式(22)进行积分:

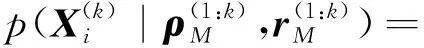
(23)

式中:M/i表示集合M中除去变量i后剩余变量的集合。

2.2 基于消息传递的多无人机协同位置估计

式(22)给出了全局概率密度函数的因子分解形式,根据无人机之间的状态相互独立与观测值之间相互独立的假设,式(22)可进一步写成

(24)

式中:n(i)表示无人机i的邻居无人机的集合。若令

(25)

则有

(26)

于是,可得到式(26)对应的因子图如图4所示。

图4 多无人机协同定位因子图模型Fig.4 Multi-UAV cooperative positioning factor map model

图中,fi表示无人机i从k-1时刻到k时刻的转移因子,ρi,sB表示k时刻无人机i可观测的BDS卫星集合的因子节点,ρi,sG表示k时刻无人机i可观测GPS卫星集合的因子节点,ri,j表示k时刻无人机i与邻居j之间的距离观测因子。

因为测量噪声会对观测值的可信度产生影响,所以有必要对其随机模型进行分析。通常可以假设测量噪声的随机模型服从零均值的高斯分布。卫星高度角越大,卫星信号上的噪声越小,因此可以采用高度角来描述伪距观测噪声的随机模型,采用基于高度角的正弦函数形式的随机模型来描述:

(27)

式中:σρ为伪距测量噪声的标准差;a,b均为常数,通常分别设置为0.003和0.000 2;e是伪距与载波误差比,通常可根据经验设置。

对于无人机间相对距离观测值,邻居无人机的位置精度也会对距离观测量的可信度造成影响。假设(xi,yi,zi)为待估无人机的坐标,(xn,yn,zn)为邻居无人机的坐标,邻居无人机在x,y,z轴上的定位精度分别为σn(x),σn(y),σn(z),则其在距离上引入噪声的标准差可表示为

(28)

考虑传感器自身噪声以及邻居无人机位置引入的噪声后,无人机间距离观测值的方差可表示为

(29)

式中:σUWB表示传感器自身的测距噪声标准差。

结合多无人机协同定位因子图模型以及消息传递算法式可得到无人机节点i的后验概率密度函数为

(30)

由于假设所有观测噪声服从零均值高斯分布,所以因子图上所有的消息均服从高斯分布。

在消息传递过程中也仅需传递均值和方差这两个参数信息即可。图5给出了一个简化多无人机协同定位因子图模型。

对于从k-1时刻到k时刻的转移因子节点传递给无人机变量节点的消息μf→Xi,其概率密度函数的均值和方差由状态一步预测公式(10)以及均方误差一步预测公式(11)给出。

对于卫星因子节点传递给无人机变量节点的消息μs→Xi,其概率密度函数为

(31)

式中:A为归一化因子,Xi表示无人机i的坐标向量为未知量,Xs表示卫星坐标向量是已知的,‖·‖表示欧氏距离,bi是接收机钟差也是未知的。均值为伪距观测值ρi,s,方差为σρ,其计算方法如式(27)所示。

对于距离因子节点传递给邻接无人机变量节点的消息μr→Xi,其概率密度函数为

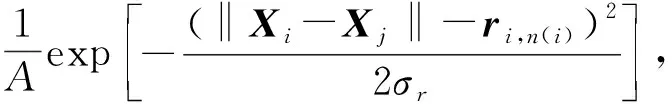
(32)

式中:A为归一化因子;Xi表示无人机i的坐标向量为未知量;Xn(i)表示邻居无人机n(i)的坐标向量,其值为邻居无人机传递给该因子节点的消息μXn(i)→r的均值;ri,n(i)为距离观测值,是该密度函数的均值;σr为方差,其计算方法如式(29)所示。

对于无人机变量节点传递给邻接距离因子节点的消息μXn(i)→r,其概率密度函数的均值和方差可通过参数估计方法获得。考虑到消息服从高斯分布,观测方程为非线性方程,且消息传递算法是一个迭代近似的过程,因此本文采用迭代滤波估计方法对此类消息的均值和方差进行估计。迭代滤波估计方法的流程如1.2节所示。

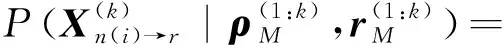
(33)

式中:n(n(i))表示n(i)的邻居节点,/i表示不包含i节点。

对于无人机变量节点自身的后验概率密度函数如式(30)所示,可以看出它也是多个邻接因子节点消息的乘积形式,因此该概率密度函数的均值和方差也可采用迭代滤波估计方法来获取。

基于上述说明,可以给出基于消息传递的多无人机协同位置估计算法流程图,如图6所示。

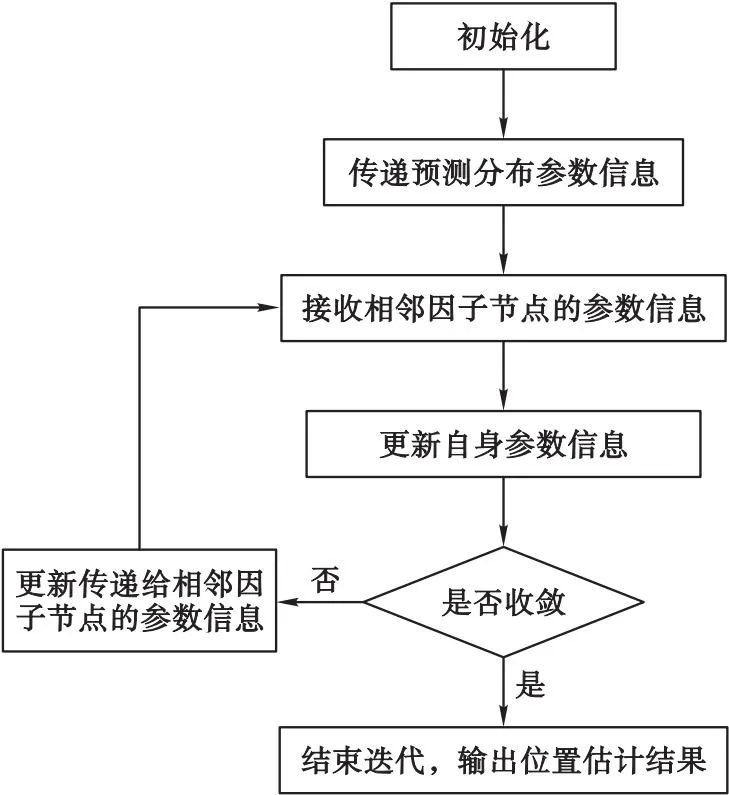
图6 多无人机协同位置估计算法流程图Fig.6 Flow chart of multi-UAV cooperative position estimation algorithm

3 仿真验证

为了验证本文所提出的分布式多无人机协同定位算法的有效性,首先设计了一组仿真实验,用于对比本文算法与传统单无人机独立定位算法的定位效果。

在本实验中,设置了3个目标节点,其真实位置坐标如表1所示。

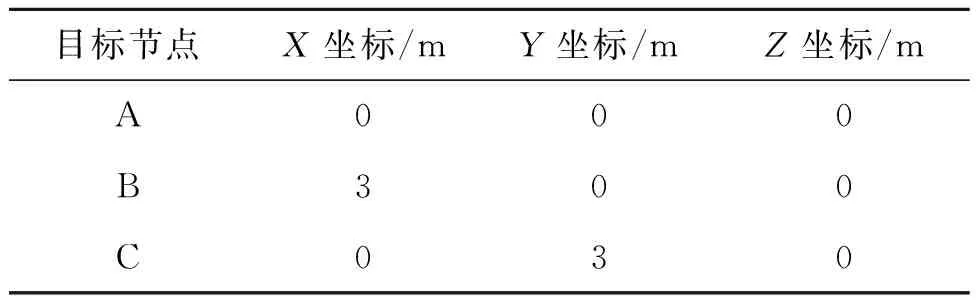
表1 目标节点真实坐标Tab.1 Real coordinates of target nodes

同时还设置了10个锚节点,其位置坐标如表2所示。

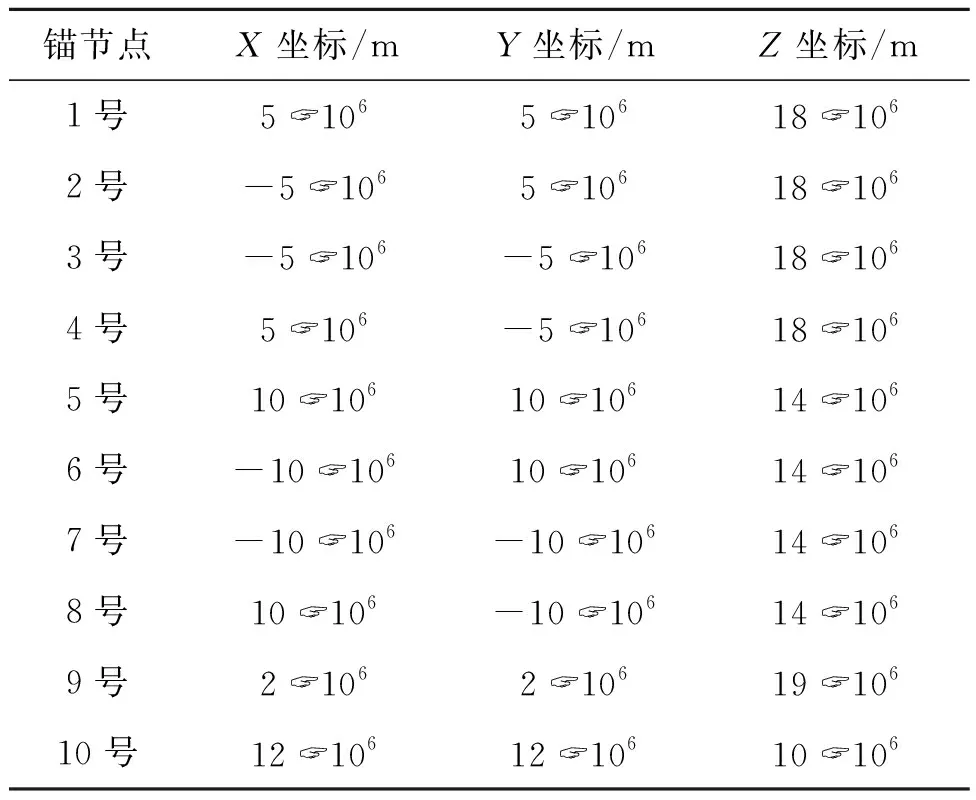
表2 锚的位置坐标Tab.2 Anchor position at coordinates

仿真实验假设:目标节点以及锚节点均处于静止状态,目标节点之间均可相互观测,目标节点与所有锚节点之间均可观测,锚节点距离观测噪声方差因子为5 m2,目标节点距离观测噪声方差因子为0.01 m2。

采用状态的均方根误差值对协同定位以及独立定位的结果进行比较,仿真结果的均方根误差(RMSE)值如表3所示。

表3 仿真定位结果的RMSE值Tab.3 RMSE values of simulation positioning results

仿真结果的绝对误差如图7—图9所示。

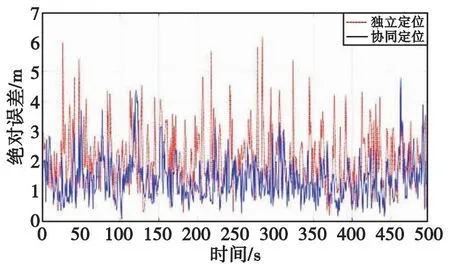
图7 节点A不同定位方式的绝对误差Fig.7 Absolute error of different positioning methods of node A

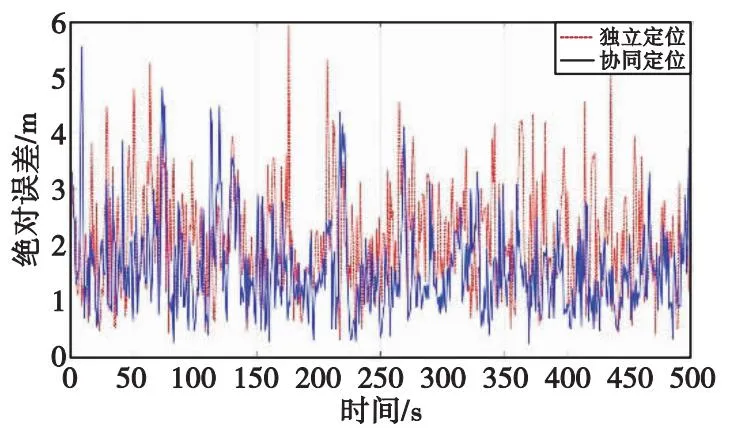
图8 无人机B不同定位方式的绝对误差Fig.8 Absolute error of different positioning methods of UAV B

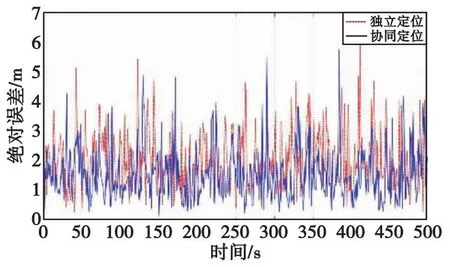
图9 无人机C不同定位方式的绝对误差Fig.9 Absolute error of different positioning methods of UAV C

图中,实线代表的是协同定位的结果,点划线代表的是独立定位的结果,不难看出,本文提出的分布式多节点机协同定位方法的定位结果要优于传统单节点独立定位的结果。另外从表3可以看出,单节点独立定位结果的均方根误差是多节点协同定位结果的均方根误差1.3倍左右。特别地,当无人机之间协同定位解算时发生交互通信中断或者不连续时,各个无人机的定位结果等同于各自导航系统独立定位的结果。因此相较于独立定位或者发生通信中断时,本文提出的协同定位方法的定位精度有着30%左右的提升。

目标节点间相对距离保持的误差曲线图如图10所示。

图10 节点间相对距离误差曲线图Fig.10 Relative distance error curve between nodes

图中,实线代表的是协同定位的结果,点划线代表的是独立定位的结果。得益于定位精度的提高,与单节点定位相比,协同定位方案下的节点定位结果更符合节点间相对距离的约束条件。

同时将本文所提的分布式多节点协同定位方法与集中式EKF多节点协同定位方法进行比较,以RMSE值作为考察对象。表4给出了对比仿真定位结果的RMSE值。

表4 分布式与集中式对比仿真实验结果的RMSE值Tab.4 RMSE values of centralized and distributed simulation results

图11—图13给出了集中式算法与分布式算法的对比结果。

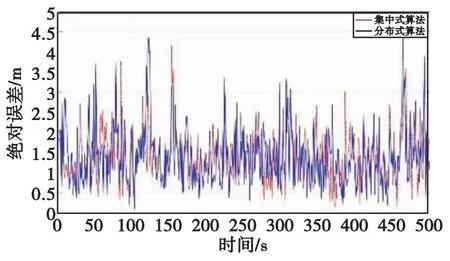
图11 节点A集中式与分布式定位的绝对误差Fig.11 Comparison of RMSE for centralized and distributed positioning of node A

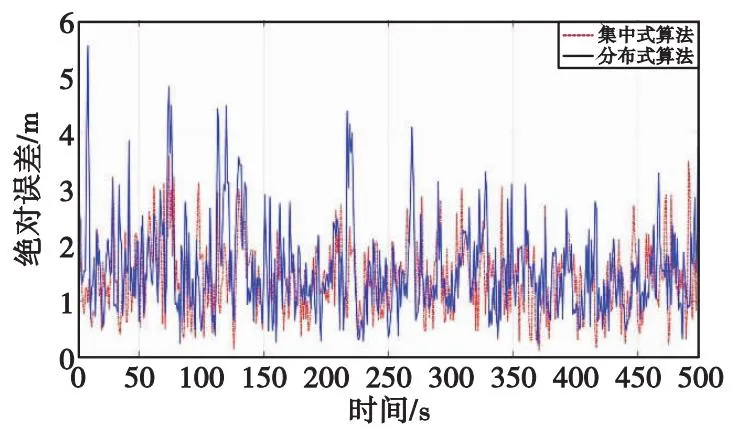
图12 节点B集中式与分布式定位的绝对误差Fig.12 Comparison of RMSE for centralized and distributed positioning of node B

图13 节点C集中式与分布式定位的绝对误差Fig.13 Comparison of RMSE for centralized and distributed positioning of node C

图中点划线代表集中式EKF算法的定位结果,实线代表本文所提分布式算法的定位结果。相比于分布式算法的定位结果,集中式算法的定位结果曲线波动较小,定位精度要优于分布式算法,但从总体来说差异并不巨大。仿真结果表明,集中式算法的定位精度优于分布式算法的定位精度。这是由于集中式算法是根据全局信息进行最优估计,而分布式算法则是根据局部信息进行最优估计,并且通过消息传递机制实现对全局最优估计的近似,因此不可避免地会存在一定程度的精度丢失,然而考虑到集中式算法在实际应用中的局限性以及分布算法的优越性,该10%的定位精度差距是可以接受的。

4 结论

本文提出了多无人机协同定位的因子图模型,并根据消息传递算法进行无人机间信息的传递,最后使用迭代滤波算法对无人机的位置进行估计,实现了基于无人机间距离观测以及卫星距离观测的多无人机分布式协同定位。仿真结果表明该分布式协同定位算法有着接近于集中式协同定位算法的定位精度,并且优于单点独立定位算法的定位精度。后续将在搭载了高性能嵌入式计算机Jetson xavier NX,GPS,UWB,ZigBee,Pixhawk等主要电子设备的多架四旋翼平台上进行算法验证。