脉冲噪声下基于CNN-FRFT的线性调频信号参数估计方法
卢景琳,郭 勇,杨立东
(1.内蒙古科技大学信息工程学院,内蒙古 包头 014010;2.内蒙古科技大学理学院,内蒙古 包头014010)
0 引言
线性调频(linear frequency modulation, LFM)信号是一种典型的非平稳信号,其瞬时频率随时间呈线性变化。LFM信号具有大时宽带宽积,相较于单频信号和窄带信号而言,LFM信号的抗干扰能力更强,因此被广泛地应用于雷达、声纳、水声通信及地震勘测等领域[1-3]。由于噪声在信号的采集和传输过程中难以避免,所以探索噪声环境下LFM信号的检测与参数估计方法是必要的。大多数参数估计方法通常假设噪声为高斯噪声,而实际环境中由突发性干扰引起的噪声一般都不服从高斯分布,这使得基于高斯假设的参数估计方法无法满足实际需求。脉冲噪声是一种典型的非高斯类噪声,它具有持续时间短和幅值大的特性,并表现出明显的尖峰。因此,探索脉冲噪声下LFM信号的检测与参数估计方法,提高目标探测的抗干扰性对雷达、声纳、水声通信及地震勘测等领域具有重要的理论和实际意义。
近年来,学者们提出了一些针对脉冲噪声的去噪方法,如滤波器、限幅器、分数低阶统计量、非线性幅值变换函数、相关熵等[4-12]。这些方法通过滤波器或非线性函数抑制大幅值脉冲噪声,再利用LFM信号的时频特征或分数谱特征来估计参数。2018年,文献[9]使用Sigmoid函数抑制脉冲噪声,进而基于分数功率谱密度(fractional power spectrum density, FPSD)实现LFM信号的参数估计。2020年,文献[10]使用扩展线性chirplet变换来抑制脉冲噪声,然后利用Radon变换实现信号的参数估计。2021年,文献[11]构造了一种压缩变换(compress transform,CT)函数来抑制脉冲噪声,进而结合分数阶傅里叶变换(fractional fourier transform,FRFT)来估计LFM信号的参数。2022年,文献[12]通过分数低阶变换函数来抑制脉冲噪声,然后利用同步压缩变换方法估计LFM信号的瞬时频率。这些方法可以抑制脉冲噪声对LFM信号参数估计的干扰,并且容易实现,但是也存在一些不足,如分数低阶统计量方法依赖脉冲噪声的先验知识和参数的选取,并且在低信噪比下该方法的性能明显下降,噪声鲁棒性差;非线性变换方法如IB-NAT(increasing bounded-NAT)函数等在实测噪声下的去噪性能急剧下降,泛化能力较差。
深度学习以强大的特征学习能力被广泛应用于信号和图像处理的各个领域,展现出良好的泛化能力。目前,有学者将深度学习应用于LFM信号的检测与参数估计中[13-16]。如文献[13]提出一种基于Wigner-Ville分布的复值卷积神经网络,使用此网络从LFM信号的时频图中直接提取特征。相较于平滑伪Wigner-Ville分布上的线段检测和FRFT滤波这两种传统方法,该方法在精度和计算效率均有显著的提高。文献[14]使用去噪卷积神经网络去除高斯噪声,进而使用Radon-Wigner和FRFT估计LFM信号的参数,在低信噪比下仍具有良好的性能。文献[15]提出了一种高斯噪声下基于DeepLabV3+的雷达信号检测方法,将LFM信号的时频图输入 DeepLabV3+网络中进行训练,实现对LFM信号的检测,有效地改善了低信噪比下检测性能不足的问题。但是,深度神经网络的训练需要大量的计算且计算复杂度高,而网络体量的增加导致了训练过程较为缓慢,这极大地限制了其在信号处理中的应用[16]。
为了解决上述存在问题,本文提出一种脉冲噪声下基于CNN-FRFT的LFM信号参数估计方法。该方法使用CNN去除脉冲噪声,然后利用LFM信号的分数谱特征进行参数估计。通过构建轻量级的CNN模型,本文方法不仅可以有效去除LFM信号中的大幅值脉冲噪声,而且极大地压缩了网络的训练时长。
1 脉冲噪声
1.1 脉冲噪声模型
在实际工程应用中,脉冲噪声通常由持续时间短和大幅度的不规则脉冲尖峰构成,具有明显的脉冲尖峰特性。1925年,Levy提出α稳定分布模型,该模型满足广义中心极限定理,可以很好地拟合脉冲噪声。α稳定分布是一种非高斯分布,其概率密度函数没有统一的解析表达式,通常采用如下的特征函数来描述[17]:
φ(t)=exp{jδt-γ|t|α[1+jβsgn(t)]ω(t,α)},
(1)
式中:
(2)
α稳定分布的参数包括特征指数α、偏斜参数β、分散系数γ以及位置参数δ。α的取值范围为(0,2],决定脉冲噪声的强度。α越小,出现大幅值脉冲的概率越大。β的取值范围为[-1,1],决定分布的偏斜程度。当β=0时,称为对称α稳定分布。γ决定了样本值与均值的偏离程度,类似于高斯分布的方差。δ决定概率密度函数在x轴的位置。图1展示了不同α值下服从α稳定分布的随机变量,其他三个参数为:β=0,γ=1,δ=0。从图中可以看出,α值越小,噪声的脉冲特性越明显,出现大幅值脉冲的概率就越大。
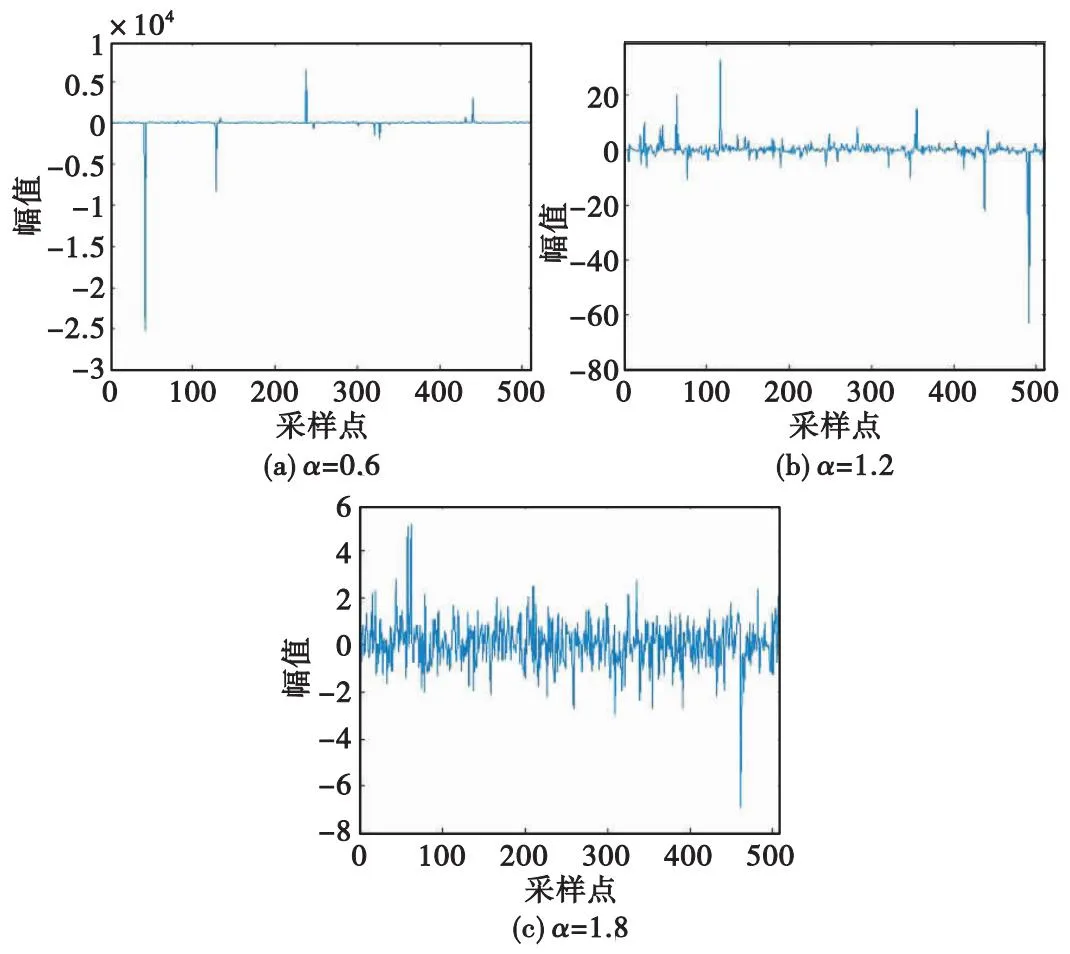
图1 不同α值下服从α稳定分布的随机变量Fig.1 Random variables conforming to the stable distribution of alpha with different α
由于噪声方差在α稳定分布下没有意义,引入广义信噪比(generalized signal noise ratio, GSNR) 来衡量随机脉冲噪声的强度,其定义为[18]
GSNR=10lg(σ2/γ),
(3)
式中:σ2为信号的方差,γ为α稳定分布的分散系数。
1.2 脉冲噪声对LFM信号分数谱的影响
假设雷达发射的信号为[19]
(4)
式中:rect(t/T)表示矩形函数,T为脉冲宽度,fc为载波频率,μ为调制频率,μ=B/T为调制频率,B为带宽。回波信号经过解调和脉冲压缩后可近似表示为
(5)
式中:τ为延迟时间,c为光速,v为目标速度,tm是在相参处理间隔内脉冲到脉冲的慢时间。因此,动目标雷达回波信号的模型可表示为
(6)
式中:f0表示初始频率,k表示调频率。为了便于CNN进行训练,本文使用的LFM信号模型为
x(t)=sin(2πf0t+πkt2)。
(7)
分数阶傅里叶变换能够提供信号从时域到频域的任意分数域信息,从而为信号的分析和处理提供了更广阔的视角和更多样的维度[20]。FRFT的数学定义为

(8)
式中:ρ=pπ/2表示旋转角度,p∈(0,2]表示变换阶数。Kρ(t,u)是分数阶傅里叶变换的核函数,表达式为
(9)
假设y(t)为含噪的LFM信号,可表示为
y(t)=x(t)+n(t),
(10)
式中:x(t)表示纯净LFM信号,n(t)表示随机脉冲噪声,服从对称α稳定分布。
利用FRFT建立含噪信号的分数谱,并与纯净信号的分数谱对比,结果如图2所示。

图2 含噪和纯净LFM信号的分数谱 Fig.2 Fractional spectrum of noisy and clean LFM signal
从图中可以看出,由于FRFT的核函数为正交线性调频函数,LFM信号在匹配的分数域内呈现出明显的峰值特性,且峰值点位置与信号参数相匹配。而含噪信号的分数谱中,由于脉冲噪声的幅值远大于信号的幅值,真实信号对应的峰值被噪声湮没。因此,LFM信号的分数谱特征被大幅值的脉冲噪声破坏,导致后续无法对LFM信号的参数进行准确估计。
2 LFM信号的参数估计方法
2.1 CNN模型
兼顾LFM信号参数估计的精度和速度,在基本不影响参数估计精度的前提下,本文构建了一种轻量化的CNN模型对信号进行去噪。该轻量级CNN模型主要由输入层、标准卷积层以及输出层构成,其中标准卷积层包括一维卷积层、批量归一化层(BN层)以及Tanh激活函数[21]。该模型压缩了神经网络的层数,共有12层,其中包含4个一维卷积层,3个批处理归一化层以及3个Tanh激活函数。卷积过程中,卷积核在一维输入信号上滑动来学习特征。一维卷积层的输出Gi为
Gi=Yi-1*Wi+Bi,
(11)
式中:i为层数,Wi为权重值,Bi表示偏差项。BN层的归一化激活式为
(12)
式中:μ为平均值,δ为方差,ε=0.000 01。BN层的输出Zi为
(13)
式中:λ为比例因子,β为偏移量。BN层可以有效处理层间数据分布问题,并且使训练速度及模型精度显著提升。激活函数设置为双曲正切函数Tanh,数学表达式为
(14)
网络的损失函数为
(15)
式中:M为小批量的大小。网络训练过程中使用adam优化器及反向传播算法来调整网络的权重和偏置,并将损失函数作为反向优化的指标,使网络的半均方误差损失值不断降低达到最优值。
2.2 参数估计
本文提出一种脉冲噪声下基于CNN-FRFT的LFM信号参数估计方法,该方法改善了传统参数估计方法在强脉冲噪声下噪声鲁棒性弱和泛化能力差的问题。首先,基于Matlab生成LFM信号和随机脉冲噪声,将脉冲噪声加入LFM信号中构造数据集;其次,将数据集输入CNN进行训练和测试,并基于训练好的模型去除随机脉冲噪声;最后,利用LFM信号的分数谱特征估计其参数,参数估计的数学模型为
(16)
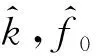
本文提出的参数估计方法的算法流程如图3所示,具体步骤包括:

图3 LFM信号参数估计的算法流程Fig.3 Flow chart of LFM signal parameter estimation
步骤1 生成LFM信号:利用式(7)生成纯净LFM信号;
步骤2 生成含噪信号:利用式(1)生成随机脉冲噪声,通过添加加性噪声生成含噪LFM信号;
步骤3 数据集构建:构建训练集、验证集和测试集;
步骤4 模型训练:将数据集输入CNN进行训练和测试,并对模型进行评估;
步骤5 信号去噪:利用训练好的CNN模型去除含噪信号中的随机脉冲噪声;
步骤6 参数估计:利用FRFT建立去噪信号的分数谱,基于峰值点位置估计LFM信号参数。
3 仿真分析
3.1 模型训练
本文中,设置LFM信号的参数为:采样频率fs=256 Hz,时宽T=2 s,调频率和初始频率的变化范围为k=[5,10],f0=[15,20],步长均为1。本文使用Matlab 2021b中的深度学习工具箱来搭建并训练CNN,网络参数见表1。在LFM信号中添加GSNR=-1 dB的随机脉冲噪声,噪声的参数为α=1.2,β=0,γ=0.63,δ=0。如无特殊说明,下文所述CNN均为构建的轻量级CNN模型。在GSNR=-1 dB下构建训练集和验证集,分别包含54 000和10 800个样本。

表1 网络参数表Tab.1 Network parameter table
如图4所示,训练集和验证集的Loss曲线都呈下降趋势并逐渐趋于平稳,均方根误差(RMSE)的终值为0.332 3。基于同一平台并使用相同的训练集,DCNN模型的训练用时为CNN模型的7倍,RMSE的终值为0.148 8。虽然CNN模型的RMSE的终值较高,但此时仍然能够保持LFM信号的分数谱特征,也就是说训练时间的大幅减少并未影响参数估计的精度。

图4 模型的训练曲线Fig.4 Training curve of CNN model
3.2 性能分析


图5 含噪和去噪LFM信号的分数谱(GSNR=-1 dB)Fig.5 Fractional spectrum of noisy and denoised LFM signal(GSNR=-1 dB)


图6 含噪和去噪LFM信号的分数谱(α=1.4)Fig.6 Fractional spectrum of noisy and denoised LFM signal(α=1.4)

图7 含噪和去噪LFM信号的分数谱(α=0.8)Fig.7 Fractional spectrum of noisy and denoised LFM signal(α=0.8)


图8 含噪和去噪LFM信号的分数谱(GSNR=1 dB)Fig.8 Fractional spectrum of noisy and denoised LFM signal(GSNR=-1 dB)

图9 含噪和去噪LFM信号的分数谱(GSNR=-3 dB)Fig.9 Fractional spectrum of noisy and denoised LFM signal (GSNR=-3 dB)
3.3 对比分析
此外,设置α的变化范围为[0.6,1.4],间隔为0.2,GSNR的变换范围为[-7 dB,7 dB],间隔 2 dB。在上述范围内随机生成脉冲噪声,并加入纯净LFM信号中生成含噪信号来测试本文方法在不同脉冲噪声环境下的参数估计性能。在随机的脉冲噪声下,分别进行100次蒙特卡洛实验,将本文方法与Sigmoid-FPSD[8],CT-FRFT[11]和IBNAT-LVD[5]3种参数估计方法进行比较,并采用RMSE来评价参数估计的精度。另外,在得到的100组估计结果中,应用了离群点检测算法来进一步提高本文方法的参数估计精度。最终,基于4种方法得到的RMSE随GSNR的变化曲线见图10和图11。

图10 中心频率的RMSE变化曲线Fig.10 RMSE curve of center frequency
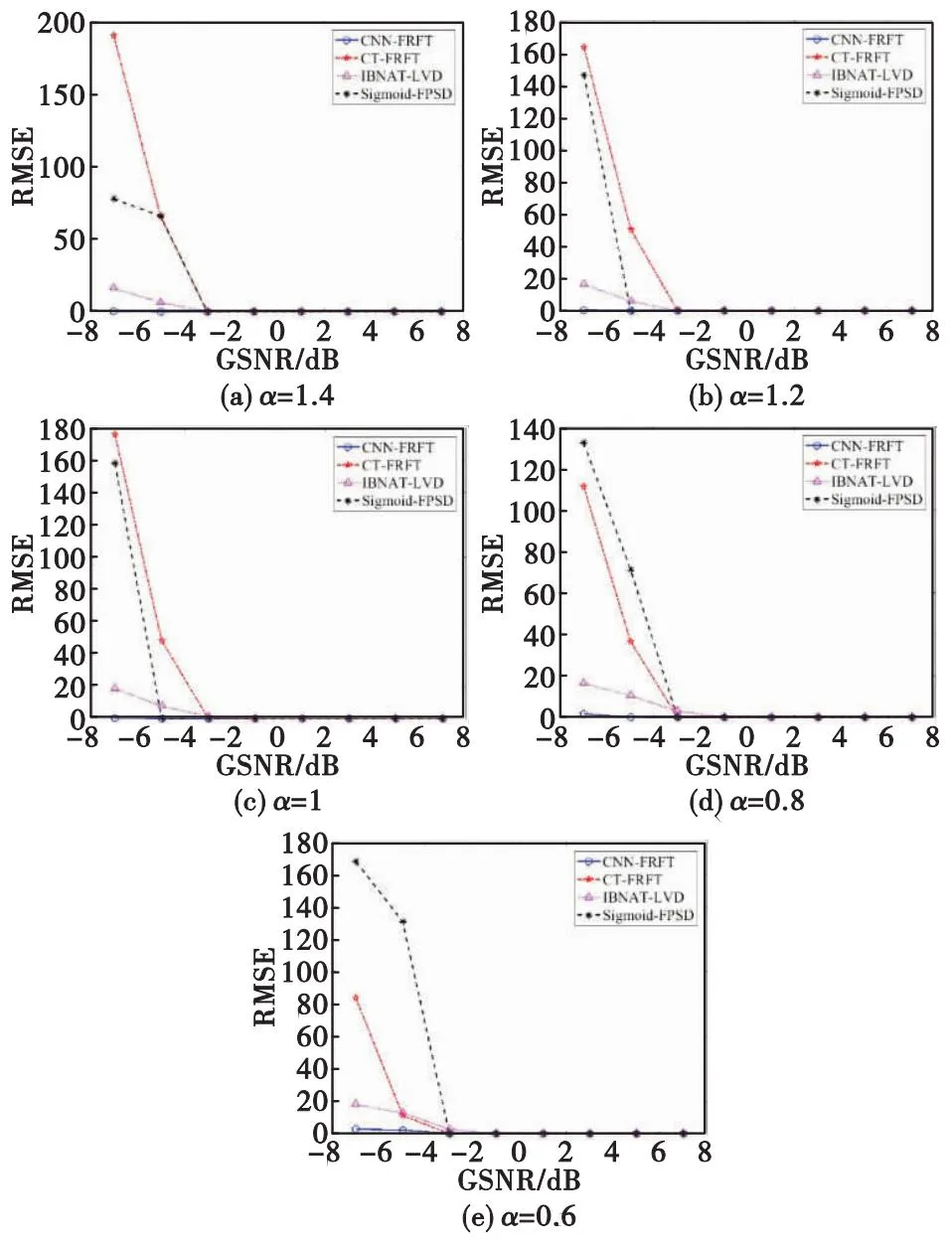
图11 调频率的RMSE变化曲线Fig.11 RMSE curve of frequency modulated
如图10和图11所示,在α≥0.8的脉冲噪声环境下,当GSNR≥-3 dB时,4种方法都展现出了良好的参数估计性能。当GSNR<-3 dB时,CT-FRFT,IBNAT-LVD以及Sigmoid-FPSD方法的参数估计性能下降,无法准确估计LFM 信号的参数,但是,CNN-FRFT方法仍然可以准确估计LFM信号的参数。特别是在α=0.6的强脉冲噪声环境下,当GSNR<-3 dB时,调频率和中心频率的RMSE都开始逐渐增加,说明4种方法的参数估计性能都开始下降。但是,CNN-FRFT方法得到的RMSE仍然是4种方法中最小的,优于其他3种方法。
为了直观地展现强脉冲噪声环境下CNN-FRFT方法的优势,将α=1,GSNR=-7 dB下4种方法的蒙特卡洛实验结果通过散点图呈现(见图12),图中的斜线为LFM信号的瞬时频率。从图中可以看出,CNN-FRFT方法得到的100组估计结果中,大部分估计值分布在瞬时频率附近,只有少部分估计值发生偏离,离群点检测的应用可进一步将离群点剔除。而对于其他3种方法,100组估计结果中的大多数点偏离瞬时频率,尤其是CT-FRFT和IBNAT-LVD,只有少数的估计值分布在瞬时频率附近。因此,从散点图可得,强脉冲噪声环境下CNN-FRFT方法在参数估计的稳定性方面优于其他3种方法。也正是因为这个原因,强脉冲噪声环境下本文所应用的离群点检测算法可进一步提高参数估计的精度。综上所述,本文所提出CNN-FRFT方法在参数估计的稳定性和精度方面优于其他3种方法,尤其是在强脉冲噪声环境下的优势更加明显。

图12 参数估计结果的散点图Fig.12 Scatter plot of parameter estimation results
3.4 实测数据验证
采用美国国家公园采集的冰川湾水下声响中的“中度风”[22]作为实测脉冲噪声来分析CNN的泛化能力(见图13(a))。通过调整噪声幅值,在参数为f0=15.5 Hz,k=5.5 Hz/s的纯净LFM信号中加入GSNR=0.44 dB和GSNR=-2.54 dB的实测脉冲噪声,如估计结果与纯净LFM信号的参数一致或相近时,则说明该方法在实测脉冲噪声环境下能够估计LFM信号的参数。对含噪信号进行FRFT,得到的分数谱如图13(b)和(c)所示。
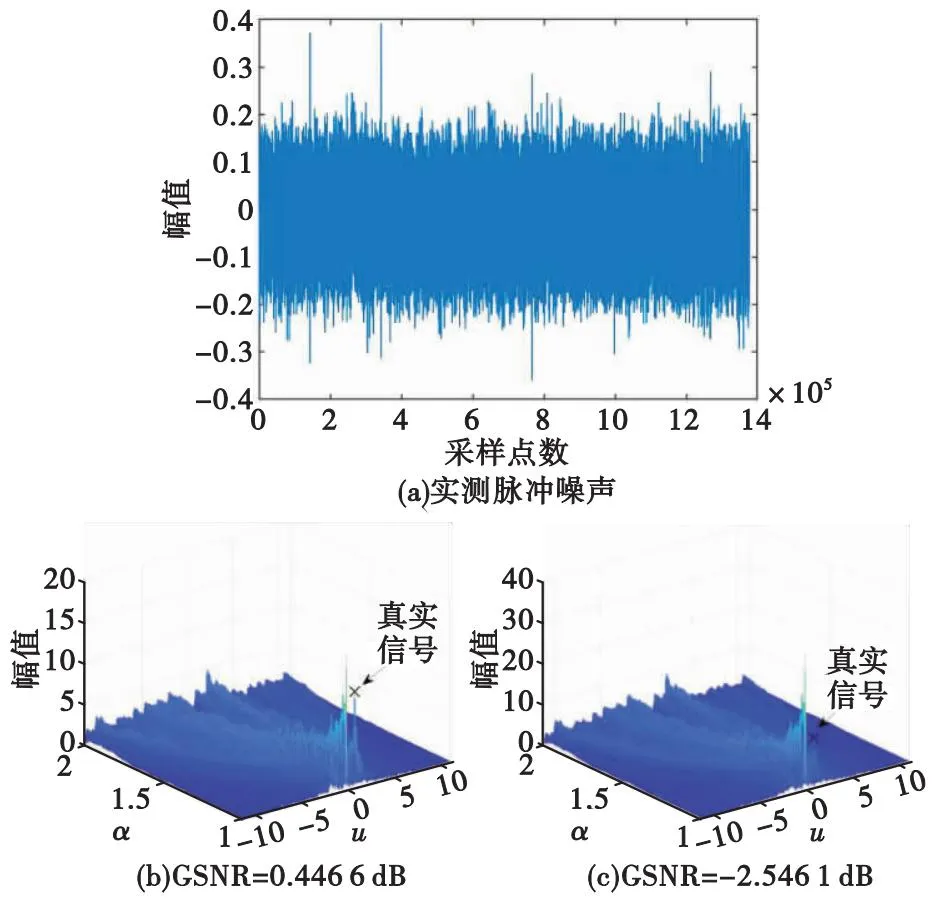
图13 实测脉冲噪声和含噪信号的分数谱Fig.13 Fractional spectrum of the noisy signal and measured pulse noise
从图中可以看出,噪声所产生的峰值大于真实信号对应的峰值,伪峰的存在使得LFM信号的参数无法准确估计。接下来,同样基于前述的4种方法对实测脉冲噪声环境下的LFM信号的参数进行估计,估计结果见表2。

表2 基于实测脉冲噪声的参数估计结果Tab.2 Parameter estimation results based on measured pulse noise
对比表2中的数据可知:当GSNR=0.446 6 dB时,CT-FRFT和IBNAT-LVD方法无法准确估计参数,而 CNN-FRFT和Sigmoid-FPSD方法能够估计出LFM信号的参数;当GSNR=-2.546 1 dB时,其他3种方法都无法准确估计LFM信号的参数,而CNN-FRFT方法仍然能够估计参数。这说明,基于非线性函数的传统方法在泛化能力方面较差。
图14展示了GSNR=-2.546 1 dB时基于4种方法提取的去噪信号的分数谱特征和时频特征。

图14 去噪信号的分数谱(GSNR=-2.546 1 dB)Fig.14 Fractional spectrum of the denoised signal(GSNR=-2.546 1 dB)
由于实测脉冲噪声并不完全服从α稳定分布,此时基于非线性函数的方法无法有效去除实测脉冲噪声,真实信号对应的峰值点完全被噪声湮没,继而无法有效估计参数。相比于图13(c),基于CNN-FRFT方法得到的去噪信号的分数谱中可以看到明显的峰值,且峰值位置与真实信号的参数相匹配。综上所述,相比于传统的基于非线性函数的参数估计方法,在实测脉冲噪声环境下本文所提CNN-FRFT方法依旧可以去除信号中的实测脉冲噪声,具有较好的检测和参数估计性能,进而说明本文方法具有较好的泛化能力。
4 结论
本文提出了一种脉冲噪声下基于CNN-FRFT的LFM信号参数估计方法,该方法通过CNN模型去除大幅值的脉冲噪声,进而利用LFM信号的分数谱特征估计其参数。与基于非线性函数的传统方法相比,本文方法具有更好的参数估计稳定性,离群点检测算法的应用进一步提高了参数估计的精度和噪声鲁棒性。在实测脉冲噪声环境下,本文方法依旧具有良好的性能,展现出了比传统方法更强的泛化能力。

