L 波段海水介电模型构建与误差分析

李伊凡，李新宇，王 进

（青岛大学 物理科学学院，山东 青岛 266071）

0 引言

温室效应不断积累，地气系统吸收与发射的能量不平衡，能量不断在地气系统累积，从而温度上升，全球气候变暖，导致极地海冰快速消融，在过去的几年中，北极的海冰范围呈现出一种长期的下降趋势[1]。海冰的快速消融，影响了极地海域的海洋盐度，因此对极地海域海洋盐度的观测逐渐得到重视。目前对于海面盐度的研究，大多集中在遥感卫星观测、现场实测等方面。现场观测虽然精度高，但是无法获取大范围的海面盐度数据，且费时费力。微波遥感反演是获得大范围盐度数据的有效手段。目前，国际上海表盐度遥感卫星有：欧空局ESA（European Space Agency）于2009年发射的土壤湿度和海洋盐度卫星（Soil Moisture and Ocean Salinity，SMOS）以及美国国家航空航天局NASA（National Aeronautics and Space Administration）于2011年和2015年发射的宝瓶座盐度卫星（Aquarius/SAC-D）和土壤湿度主-被动遥感卫星（Soil Moisture Active Passive，SMAP）[2-4]。盐度遥感卫星通过接收海面辐射亮温，提取海面盐度信息。由辐射传输方程可知，海面微波辐射可以表示为海面温度与海面发射率的乘积。海面发射率可以表示为平静海面发射率与粗糙海面发射率之和，其中平静海面发射率由菲涅耳方程和海水介电模型描述，是辐射计观测亮温中对海面盐度变化敏感的部分。在盐度遥感应用中，要求精度优于0.1～0.2 psu，考虑到 L 波段亮温对盐度变化的敏感性只有 0.2～0.8 K/psu，这就对海水介电常数提出了苛刻的要求[5]。

在早期研究中，STOGRYN、KLEIN、SWIFT、ELLISON 等人利用德拜表达式初步建立了海水介电常数的模型函数[6-9]。KLEIN 和SWIFT（以下简称KS）以及HO、HALL 等人分别在2.6 GHz 和1.4 GHz 的测量基础上，使用了不同的静态介电常数εs（S，T）表达式，对STOGRYN 模型进行了修正，KS 和STOGRYN 的海水介电常数模型适用于L 到 X 波段的频率范围[10-11]。MEISSNER 和WENTZ（以下简称MW）开发的另一种模型函数将介电常数数据拟合到双德拜多项式上，该多项式在更高频率下表现更好[12]。MW 模型函数在2012年和2014年基于WindSat 和AMSR 的C 波段和X波段信道的结果，对Debye 参数进行了微调[13-14]。MW 模型用于Aquarius 和SMAP SSS 反演算法。为了改进模型功能，最终提高盐度反演的准确性，乔治华盛顿大学（George Washington University，GWU）测量了1.413 GHz（遥感使用的频率）的介电常数，并于2017年基于这些实验室测量数据，将介电常数展开为S和T的三阶多项式，开发了海水介电模型函数，简称GW2017 模型[15]。此外，为了进一步研究海水在低温下的介电常数，乔治华盛顿大学又对盐度为30 psu、34 psu、35 psu，温度为-1.5～3 ℃的海水进行了测量。2021年，构建了由德拜分子共振项和电导率项组成的基于物理的模型函数，简称 GW2020（以下简称GWU）[16]。

但是，目前广泛使用在海面盐度遥感领域中的Klein-Swift 模型、Meissner-Wentz 模型在低海温时盐度反演误差较大，因此本文旨在使用更大盐度和温度范围内的实验数据发展一个包含低温条件下的高精度L 波段的介电模型。本文第1 章介绍了构建海水介电常数模型所使用的数据与方法；第2 章介绍了新模型的系数并将新模型函数与其它现有模型在介电常数模拟精度方面进行了比较；第3 章是结论。

1 数据与方法

1.1 数据

本文为了建立介电模型函数，使用了LANG、ZHOU 等人在2017年之前，在温度为0～35℃、盐度值为30 psu、33 psu、35 psu、38 psu 的情况下进行的海水介电常数的测量数据，温度间隔为5℃[17]。此外，为了进一步研究海水在低温下的介电常数，还使用了ZHOU 等人2018年之后的新测量数据[16]。

蓝色块为2018-2020年的新测量数据；黄色块为2017年之前的测量数据。图1 测量数据点Fig.1 Measurement data points

1.2 模型构建

新模型函数用盐度S和温度T的多项式表示：

式中：ε为海水介电常数；未知复系数pm,n根据测量数据，可以通过奇异值分解（Singular Value Decomposition，SVD）技术[18-19]直接求解；m、n分别表示盐度S和温度T的阶数；L表示S和T的最高阶。

在指定模型函数的多项式的阶数尚未确定时，将考虑L=3，4，5 阶的值。做出选择的标准将基于数据和模型函数预测之间的均方根误差（RMSE）。定量地表示实部和虚部的均方根误差为

式中：υ是自由度，假设数据点的个数为N=77，多项式系数的个数为M，则υ=N-M，这个差值就是模型函数施加约束后剩下的独立随机变量的个数；α和β分别为盐度和温度的数据点数量；和分别为模型函数值与实测数据的实部与虚部之差。

模型函数的系数是通过最小化介电测量数据与模型函数之间的归一化平方误差得到的。对系数的实部和虚部分别进行最小化。对于，模型函数值与实测数据之差被定义为

式中：Si为海水样品盐度的第i值；Tj为测量温度的第j值；为在Si和Tj处测量的介电常数的实部值；为模型函数在Si和Tj处的实部。根据PRESS 等人[18]，将除以实验室测量数据的标准差，得到归一化差值

式中：α和β分别为测得的盐度和温度值的个数；'2χ为代价函数[18]。

将式（3）和式（4）代入式（5），并将其化为矩阵形式，可以简化'2χ的最小化过程。然后利用SVD 技求最小解，矩阵公式的细节如下。注意：虚部系数的确定过程与此类似，虚部的代价函数记为。

将式（3）和式（4）代入式（5），得到卡方统计量：

矩阵形式下，式（6）可以写成

式中：矩阵A′由元素构成；列向量p′由多项的列向量；列向量b′由元素式系数pm,n构成，是模型函数系数构成。因此，最小化问题可以表述为求p′使（7）最小化。

矩阵A′称为设计矩阵，是一个N×M矩阵（N和M的定义见第1.2 节）。行数N等于数据点总数，列数M等于（L+1）2。矩阵A′的表达式为

式（8）中的W′为权重矩阵；式（7）中的向量b′是权重矩阵W′乘测量的介电常数值。

最后，利用SVD 技术可以找到最小解。解决方案为

2 结果与讨论

2.1 模型系数

在本节中，根据1.2 节介绍的方法，确定了模型函数多项式的阶数，并给出模型的相关系数，最后建立新模型。

对多项式类型L=3，4，5，采用SVD 方法得到模型函数表达式。基于这些模型函数，分别计算了实部和虚部的RMSE 的值。表1 列出了这些值。

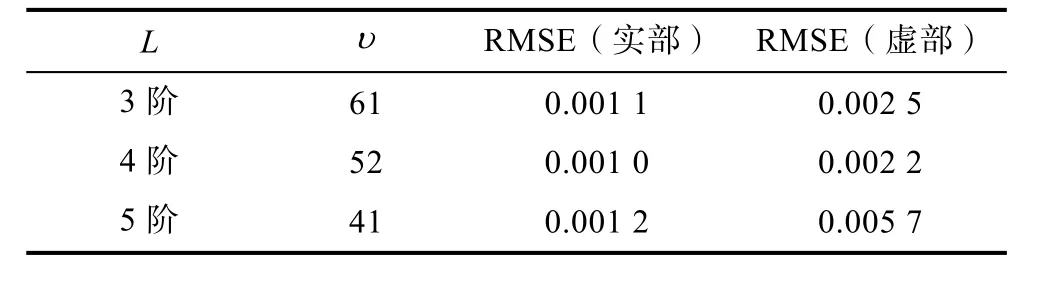
表1 不同阶次多项式模型的误差Table 1 Errors of polynomial models of different orders

由表2 可以看出，当L=4 时，实部和虚部的RMSE 均小于L=3 和L=5。因此选择L=4 作为本文模型的最高阶数。表2 和表3 给出了L=4 时多项式系数的实部和虚部。

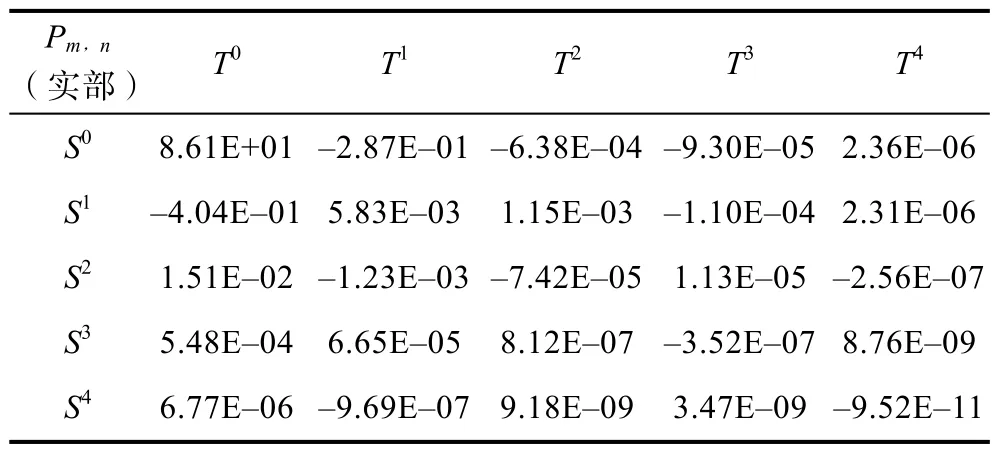
表2 模型拟合系数（实部）Table 2 Model fitting coefficient（real part）

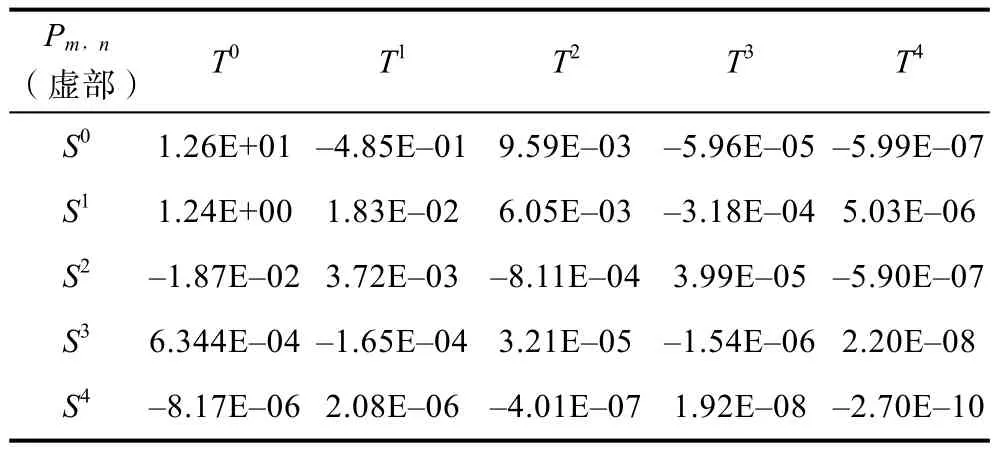
表3 模型拟合系数（虚部）Table 3 Model fitting coefficient（imaginary part）

2.2 介电常数计算结果比较

在本节中，将新模型函数与KS 和MW 模型函数以及GWU 模型计算的不同温度和盐度条件下的L 波段海水介电常数虚部和实部进行比较。

模型函数值与测量数据的RMSE 误差比较见表4。

表4 模型函数值与测量数据的RMSE 误差Table 4 RMSE errors between model function values and measured data

4 种模型函数在实验室测量点处的偏差如图2（a）-2（h）所示。

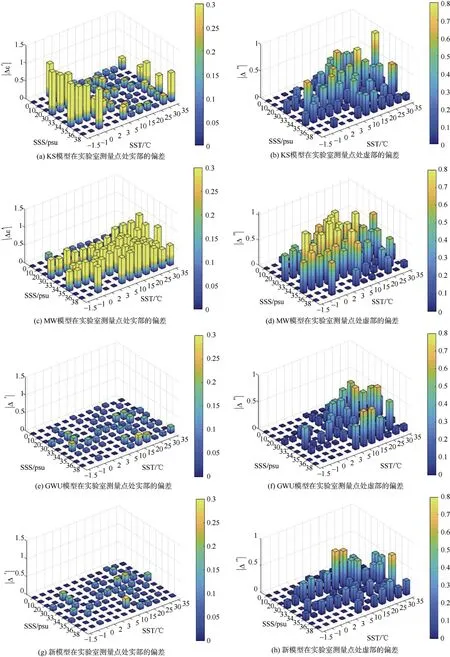
图2 4 种模型在实验室测量点的偏差对比图Fig.2 Comparison of deviations of 4 models at laboratory measurement points

由表4 知，新模型计算的海水介电常数与实验室测量数据的RMSE 误差为0.09（实部）和0.25（虚部），KS 模型、MW 模型、GWU 模型在实部比新模型对实验室测量数据的RMSE 高估了0.37、0.44、0.01；在虚部高估了0.1、0.28、0.03。所以，无论是实部还是虚部，由新模型计算的介电常数都与实测数据更吻合。为了更好地理解拟合误差，在图2（a）-2（h）中，在L= 4 的情况下，绘制了4种模型的与盐度和温度的关系图。可以看出，GWU 模型和新模型的′与测量数据的拟合都很好，虽然的偏差大于但使用相同测量数据拟合的GWU 模型和新模型的拟合效果优于KS、MW 模型。

4 种模型在盐度S=0，30，35 时计算的介电常数实、虚部对比（包含实验室数据点）如图3（a）-3（f）所示。对于0 psu，只有KS 模型计算的实部-5～5 ℃时明显偏低，其他模型非常接近，而4种模型计算的虚部仅在-5～0 ℃的低温下，有些许偏差，其他温度下基本一致；对于30 psu 和35 psu，MW 模型实部整体偏低，KS 模型实部仍然在低温时明显偏低，与实验室测量数据点有较大偏差，而4 种模型计算的虚部在-5～35 ℃的温度下几乎一致。由图可知，GWU 模型和新模型函数无论实部还是虚部均与实验室测量数据最为吻合。其中，KS 模型在5 ℃以下误差较大的可能原因是在构建时使用了温度为5、10 ℃、20 ℃、30 ℃的数据，未包含5 ℃以下的低温数据；而MW 模型所使用的数据集是从卫星反演数据中反推得到的，其数据代表性和模型的适用性受到限制，且由上述结果可知，其计算的介电常数实部在海温-5～35 ℃下，与实验室测量数据相比误差较大。

图3 4 种模型在不同盐度时介电常数实、虚部对比图Fig.3 Comparison of real and virtual dielectric constants of 4 models at different salinities

3 结束语

本文基于LANG、ZHOU 等人的实验室测量数据，采用最小二乘法和奇异值分解技术求解模型参数，构建了一个多项式形式的L 波段海水介电模型。为了验证模型的精度，本文将新模型与KS 模型、MW 模型、GWU 模型以及SMAP 卫星实测数据进行比较，发现新模型计算的介电常数误差为0.09（实部）和0.25（虚部），优于其它3个模型。