一种逆式回声仪传播时间数据的处理方法

张 宇，岳宜宛，马 芮，拜雅洁，崔学荣

（1.自然资源部海上丝路海洋资源环境组网观测技术创新中心，山东 青岛 266580；2.中国石油大学（华东） 海洋与空间信息学院，山东 青岛 266580）

0 引言

逆式回声测量仪是一种由美国罗德岛大学开发的海洋观测设备，用于记录声波从海底到海面的传播时间。当配备压力和流速传感器时，该仪器被称为CPIES（Current-Pressure Inverted Echo Sounder），可同时记录海底压力和水流信息。CPIES 的主要组件包括打捞浮标、玻璃球、安德拉流计、通讯电缆、PIES 主体及其底座。PIES 主体装有压力、温度传感器和其他功能性部件。它按预设间隔发射声波，并以0.1 ms 的时间分辨率记录声波返回时间，通常每小时进行24 次测量。

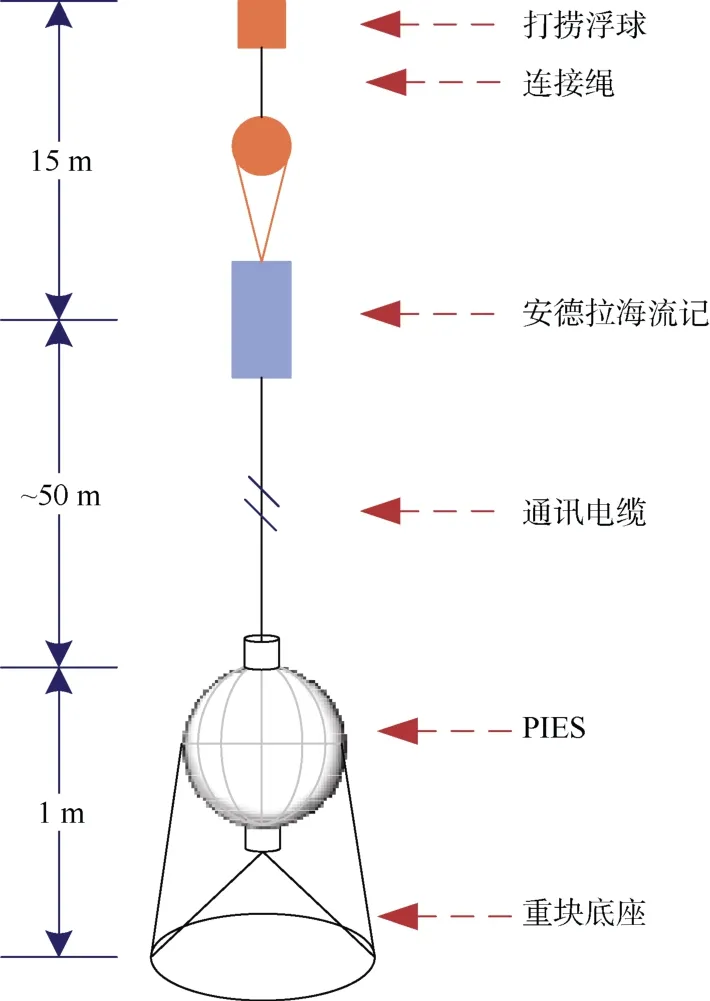
图1 逆式回声仪示意图Fig.1 Schematic diagram of IES

ROSSBY 在1969年提出利用海面至海底的声速传播时间来追踪主温跃层深度变化的概念。基于这一思想，他开发了创新工具——逆式回声仪[1]。1973年，ROSSBY 与WATTS 在MODEI 试验中首次运用IES 设备观察到了温跃层的动态变化，尽管当时的技术限制导致观测周期短且数据量有限[2]。随着20 世纪70年代后期技术进步，IES 采纳了耐压玻璃球设计并集成了高精度压力传感器，显著提升了其测量能力和作业深度[3-4]。这些优化为海洋环境监测带来了更高的可靠性与准确性，拓宽了海洋科学研究的视野。此后，IES 不断升级，演变出多功能版本以满足各种观测需求。罗德岛大学也对配备压力传感器和流速计的CPIES 进行了持续改进，这些进展极大提高了海洋监测的精度和广度，为海洋科学的进一步研究提供了坚实基础。

自21 世纪初，IES 技术经过不断累积与发展，在数据应用方面取得显著进步。WATTS、SUN 等人结合既有水文数据，发展了基于声波传播时间反演水体温度、盐度和比容异常的地转经验模态（Gravest Empirical Mode，GEM）方法[5]。此方法利用斜压流函数，将历史水文数据映射到二维空间，形成立体水文结构场，能够整合历史数据进行质量控制，并减少非线性误差，如中尺度涡流和海流造成的影响。运用CPIES 阵列和GEM，研究者能够获取精确的流速剖面。GEM 方法已被广泛应用于海洋大气边界层观测、海洋环流研究及气候变化等领域，并对评估海洋生态系统健康和资源可持续利用提供了支持[6-9]。

随后，XU 等人[10]开发了新技术，改善了CPIES数据处理，包括压力漂移校正和定标，提升了PIES在实际应用中的性能。近年来，中国科学院海洋研究所和第二海洋研究所联合开展实验，通过在南海等地区收集实地数据，深化了对黑潮、中尺度涡等现象的研究，增进了对这些海洋现象形成机理和影响因素的理解[11-13]。

为了应对海洋季节性变化对IES 声波传播时间数据的影响，本研究深入分析了季节偏差，并在数据处理过程中加以考虑，从而提高了查询时间数据的精确度。此外，由于IES 设备放置的海底深度不一，测量得到的声波传播时间数据需要划归至统一参考面（第一参考面）。本文通过确定一个统一的第二参考面，并运用线性回归分析方法，找出了第一参考面与第二参考面之间的关系，这一步骤为后续数据的标准化处理提供了必要的基础。通过这些改进，能够更准确地反映海洋内部的物理状态，有助于提升海洋科学研究的质量和效率。

1 数据

本文使用DONOHUE 和WATTS 在墨西哥湾环流研究实验中部署在海底的24 台IES 设备返回的传播时间数据（https：//web.uri.edu/ugos/presentations/）。由于设备的布放时间与回收时间并不一致，所以各台设备的时间长度并不相同，但这一点并不影响数据处理。设备的布放位置如图2所示。

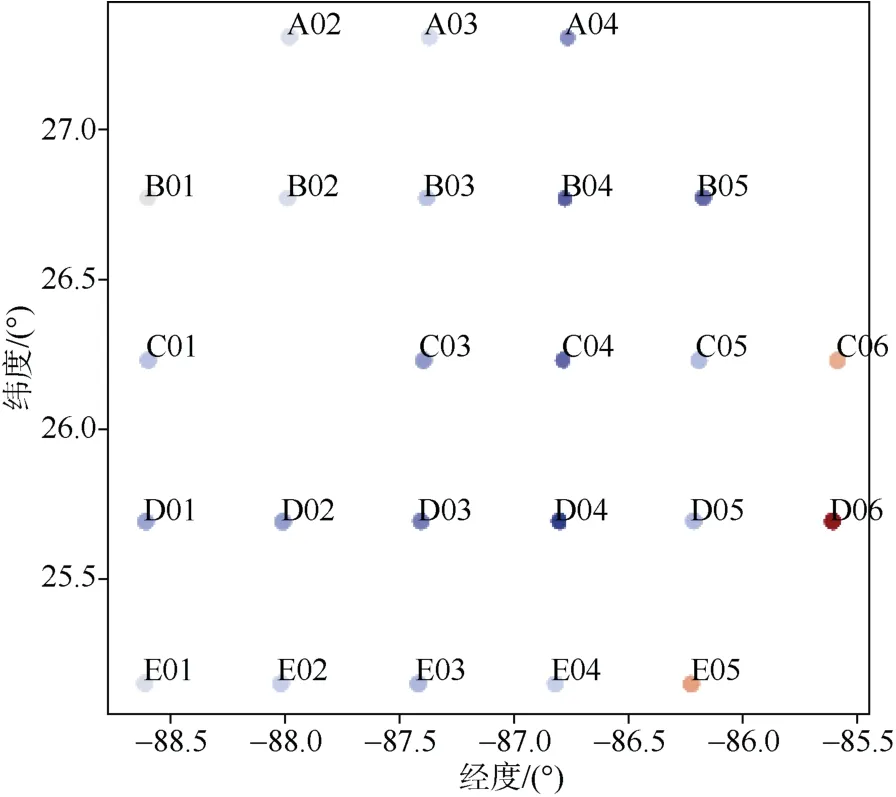
图2 IES 节点分布图Fig.2 IES node distribution diagram

由于数据处理过程与GEM 经验表的构造类似，需要历史实测剖面数据计算传播时间，因此本文也采用了大量的历史实测数据作为经验参考。数据主要来源是杭州全球海洋ARGO 系统野外科学观测研究站（http：//www.argo.org.cn/）和WOD18（ https ： //www.ncei.noaa.gov/access/world-oceandatabase-select/dbsearch.html）。数据量年度累加统计如图3所示。

图3 ARGO 剖面数据年度累加图Fig.3 Annual accumulation diagram of ARGO profiling data

2 IES 传播时间处理方法

所有的传播时间数据都需要参考一个共同的压力水平（τindex），本文我们将参考压力水平定义为1 000 dbar。GEM 的构建需要使用τindex作为查找依据，为了能够让本文分析的数据使用GEM 查找表进行剖面查找，本文也需将传播时间划归到1 000 dbar。

PIES 的工作模式被设置为每小时进行6 次声波传播时间（τ）的采样，每10 min 进行一次，每次采样发射4 个声波Ping，因此每小时总共发射24 个声波Ping。为了从这些数据中选取出具有代表性的传播时间，IES 采用了改进的四分位数方法。这个方法包括2 个阶段的窗口处理，目的是排除每小时24 个τ测量值中的异常点，并降低噪音的干扰。与处理压力和温度数据的方法相似，τ数据也通过使用四阶Butterworth 滤波器进行低通滤波，以保留低频信号并剔除高频噪声[14]。这种处理方式有助于提高数据质量，确保后续分析的准确性和可靠性。

在每个站点将测量的τ转化为τindex需要以下几个步骤：

1）从τ中去除非空间贡献（压力）。

式中：p为压力；ρ为密度；g为重力加速度；c为声速。

2）季节偏差去除。

3）转换为动力τ。

式中：bP为CPIES 站点的平均压力；g( )φ为当地的重力加速度；g0为重力加速度的初始值，可取9.8 m/s2；R是地球半径。

4）转换为参考面上的τindex。

式中：A和B是根据研究区域的历史CTD 数据计算出的系数和偏差。

5）修正τindex，根据现场利用CTD 测得的温盐剖面计算出的τ进行偏差校准。

2.1 质量负载变化

海面高度（Sea Surface Height，SSH）的变化受到多种因素的影响，主要由正压变化和斜压变化两部分组成。正压变化是指整个水柱质量的变化，通常与海水的总体重量和地球引力的相互作用有关，这种变化会导致整个水柱的上升或下降，从而影响海平面的高度。例如，当一个区域的海水增加时，通过河流输入或降雨，该区域的海平面会上升；反之，当海水减少时，例如通过蒸发，海平面则会下降。

斜压变化则与海洋内部的温度和盐度分布相关，这些参数决定了海水的密度。当水温升高或盐度降低时，海水的比容增大，即单位质量的海水体积增加，导致海平面上升；相反，当水温下降或盐度上升时，海水的比容减小，海平面下降。斜压变化通常与海洋内部的热力学和动力学过程相关，如温跃层的深浅、海流的变化等。

海面高度通过上述的2 个部分共同作用，形成了我们观测到的海平面高度。在全球尺度上，海平面高度的变化还与气候变化、极地冰盖融化、海洋热膨胀等因素紧密相关，这些都是当前海洋科学研究中的重要内容。

通过结合正压变化和斜压变化的测量数据，我们能够更全面地理解海洋动力过程，并且可以更准确地估计海平面的变化。这对于研究全球海平面上升、海洋环流、气候变化及其对海洋生态系统的影响具有重要意义。PIES 和GEM 方法的结合使用，提供了一个强大的工具，使研究人员能够从不同的角度和尺度来观察和分析海洋的物理状态。对研究海域物理性质的反演主要使用斜压分量与GEM 阵的结合。测量时间mτ由以下公式定义：

式中：sτ表示斜压变化的贡献；pτ表示正压或质量负载变化的贡献，计算方法按照公式（1）。对于正压部分质量负载来说，最大的压力变化0.1 dbar对应的往返传播时间大约为0.1 ms，而mτ的变化约为10 ms，因此pτ的变化贡献非常小。而且GEM查找表只能反映斜压引起的物理性质，因此我们需要做减法，从mτ中减去正压变化pτ。

2.2 去除季节干扰

季节性变化是指不同的季节水域的温盐结构会随着季节的变化而变化。因此从海底测得的传播时间τ也会随着季节而波动。为了去除季节变化引起的偏差，可以从τ*中减去海洋表层存在的季节变化。由于季节变化一般只对海洋表层造成影响，因此本研究将取用150 m 季节性温跃层分割线。将τ0-150和τ150-1000的对应关系画出，并利用3 次样条插值得到拟合曲线，如图4所示。

图4 利用历史水文数据计算的150～1 000 dbar 和150 dbar 对应关系的拟合曲线Fig.4 Fitting curve of propagation time of sound waves at 150 dbar and 150-1000dbar calculated using hydrological data

季节信号被定义为这条拟合曲线与实际值的残差，即τseasonal=τ0-150-τployfit。残差数据通过利用低通滤波器进行平滑处理得到主干拟合曲线，如图5所示。最后根据时间查找对应季节偏差，并将其从τs中去除得到τs,ds。

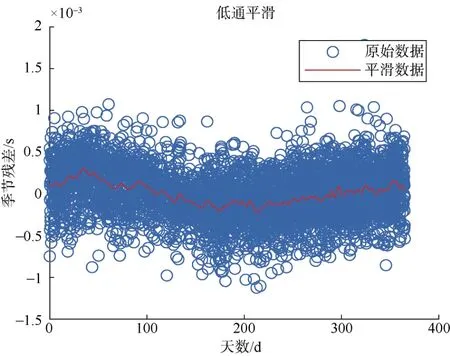
图5 季节偏差拟合曲线Fig.5 Seasonal deviation fitting curve

图6 数据校准过程演示图Fig.6 Data calibration process demonstration diagram

2.3 转化动力τ

与动力高度类似，我们使用区域水文数据计算动力τ*（我们称其为τ*）。海表面和参考压力面之间的往返传播时间由下式定义：

式中：c是声速；ρ是密度；重力加速度g是纬度λ和深度z的函数，用下式表示：

式中：a表示地球半径；z表示深度。选定斜压参考面Pref=1 000 dbar，假定g=9.8 m/s2，因此：

由于CPIES 被固定在海底进行测量，因此在CPIES 测量过程中和深度、纬度相关的重力加速度值固定不变。基于上述分析，我们将重力加速度进行拆分：

式中，a=637 100 0 m，将其带入公式（6）可得：

对于CPIES，Pref设置为bP，也就是底部平均压力。将H(z) 从积分中提出并设定为压强bP的函数，结合公式（8）得到：

变化可得：

根据经验可以近似认为：

联立上述方程可得：

最后将上式中的mτ用去除掉质量负载和季节性信号的τs,ds替换即可得到动力τ*。

2.4 将τ*转化到 τ 0 -1000（ τindex）

由于IES 所处位置为海底，深度较大，实测的温盐剖面数据大多无法达到对应深度，如果强行转化会带来巨大的拟合偏差。因此还需要确定第二参考面来将所有超过第二参考面的时间转移到该压力面上。本文设定第二参考面为1 500 m，参考时间按照下式计算：

τindex=A·τ1500+B表示1 500 dbar 深度至底部的往返传播时间，将历史水文数据1 500 dbar 以下的数据进行平均来计算该传播时间。

在得到第二参考面传播时间后，即可将其转移到第一参考面1 000 dbar 上。由于历史数据基本可以实现2 个参考面深度的覆盖，因此可以利用数据来拟合对应线性关系，采用的计算关系如下所示：

式中：A和B表示系数，由历史剖面数据计算拟合所得，分别表示线性关系的斜率和偏移。根据公式可知，如果采用的历史数据较少，拟合误差就会很大，进而影响时间的转化结果。

2.5 校正 τindex

对于IES 测量实验，一般都会实地进行全水深的CTD 测量作业，该测量深度基本在2 000～3 000 dbar。这一深度已经满足了τindex的定义参考深度，因此，针对每个站点实测得到温盐剖面应用公式（6），即可得到真实的传播时间，将其和2.4 节计算得到的T做差求得偏移量，用该偏移量对全体数据进行校准即可得到最终的传播时间数据T。

3 传播时延信息的应用

3.1 传播时间计算

GEM 技术是一种从垂直积分量确定海洋垂直剖面的方法[4，15-16]。历史水文数据用于计算温度T、盐度S和特定体积异常δ的特征关系，作为压力p和垂直集成量的函数。这些函数之间的映射关系构建出GEM 中的对应表。

本文的研究主题为墨西哥湾区域的温盐环流现象。本节将处理过的历史温盐深数据进行数据预处理后，并对每个剖面进行划归，得到参考传播时延。对其深度分辨率进行拟合，建立拉格朗日矩阵，将已有的温盐深数据投影到此二维空间上，从而建立传播时延与温度、盐度以及比容异常的经验关系，最后针对构建出的经验模态进行分析。

由于设备分布不均，历史温盐压剖面深度不一，均无法达到IES 设备深度。为更好对地转经验模态进行查表匹配，需要统一计算得到各个剖面的参考传播时延（取压力面为1 000 m 时的传播时延定义为τ1000），用该参考传播时延进行GEM 构建。传播时间的计算关系式如下：

式中：p为海水压力；g为重力加速度，取为9.82m/s ；

ρ是海水的密度；C 是海水的经验声速。其中经验声速和密度都是温度T，盐度S 和压力P 的函数。本文使用MATLAB 中的GSW 工具箱中提供的函数计算海水经验声速和密度。

3.2 GEM 阵构建

本节具体介绍了温度GEM 阵的构建。温度地转经验模态具体依赖于历史的水温剖面与参考传播时间τ1000，首先需要将传播时间τ1000从小到大进行排序作为坐标点中的x向量，并将每个剖面上该深度下的所有温度、盐度以及比容异常作为坐标点中的y向量，共同合成坐标点，然后通过3 次样条拟合对每个深度下的所有坐标点进行拟合，拟合时垂向的分辨率为10 dbar（从0～1 000 dbar），40 dbar（从1 000～2 000 dbar），这是由于剖面数量随着深度的增加而减少，因而数据的密度随深度而减小，因此压力网格垂直分辨率减小并允许3 次样条中的平滑参数随深度减小。而对于温度GEM 阵就是得到每一个深度上传播时延与该深度下所有温度的统计关系的拟合，如图7所示（以1 000 dbar 的拟合关系为例）。

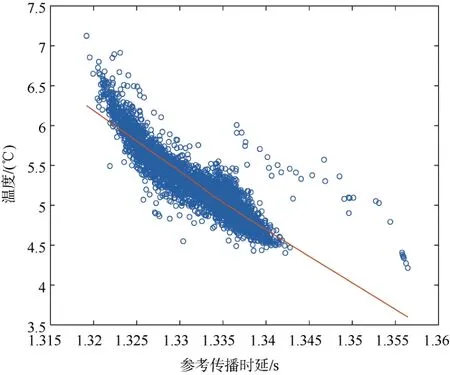
图7 1 000 dbar 下3 次样条拟合的温度与传播时间的关系Fig.7 Relationship between temperature and propagation time of cubic spline fitting at 1 000 dbar

最后由各个分辨率下的所有拟合曲线建立散点的拉格朗日矩阵，从而构建温度GEM 阵，考虑到深度2 000 m 以下的变化较小，因此本文只取了2000 m以上的温度GEM 剖面展示，图8 为温度GEM 阵。

图8 GEM 温度查找表Fig.8 GEM temperature query table

从其中基本上可以看到一个简单的关系，对于某一个深度来说，τ1000越小，对应的温度相对要高，因此便可以通过相应的传播时延τ1000来对应查出此传播时延对应的温度。

盐度及比容异常的经验模态与温度构建类似，需要注意的是，由于海洋中盐度值的差别变化与温度而言较小，会出现离群点和闭合现象。

3.3 流场计算

近年来，出现了多种计算海流的方法。计算地转流的传统方法主要包括动力高度法、 螺旋方法、盒子逆方法、伯努利方法以及P矢量方法[17-19]。

在上述介绍的方法中，动力高度法是最常用的一种计算地转流方法。它是目前可以利用单断面资料处理的唯一手段，同时也是一种可以充分利用温盐资料的有效方法。

其他4 种方法计算的都是绝对地转流，虽然有相同的动力精度（地转平衡、静力平衡和密度守恒），但因处理方法各异，导致不同的方法有不同级别的误差。

3.3.1 科氏力

只有在海水相对地球运动时，科氏力才会产生，否则它的数值只能为0。当研究主体是地转流时，水平压强梯度力则是造成海水运动的主动力，只有当海水的等压面和等势面发生倾斜，即所谓的斜压场出现时，才可以满足水平压强梯度力形成的前提条件。

3.3.2 地转流

地转流是在不考虑海水的湍应力的情况下，压强梯度力水平分量与科氏力平衡时的稳定流动。是由海面高度或海水密度变化所引起的水平压强梯度力和地转偏向力（科氏力）相平衡的产物。

由于地转流忽略了海水本身的湍流摩擦力，所以它是一种理想状态下的海流。

海洋中，海水受地球引力和地球自转产生的惯性离心力的合力即为重力，重力场中的每一点均有相应的位势，位势相同的点组成等势面；静压强相等的点则组成等压面。当等压面与等势面不重合时，等压面相对等势面发生倾斜，因水平压强梯度力的作用，海水将在受力方向上产生运动。海水开始流动之后，地转偏向力便相应起作用，在北半球使海水流动的方向不断向右偏转，在南半球相反。

若不考虑摩擦力的影响，当水平压强梯度力与地转偏向力取得平衡时，形成稳定的地转流。

其计算公式如下：设在与海流垂直的断面上有A、B两站，两站之间的距离为，任意选取 2 个等压面

式中：v为等压面上的地转流速；ΔD为两等压面间的动力高度差；f为科氏参数；pΔ 为压强间隔；Aα为Δp范围内的比容平均值。这里需要说明的是，此种方法只能计算出A站和B站相对于流速零面的地转流速的平均值。根据静压方程：

式中：p为等压面上的压强；g为重力加速度。因此，计算时可近似的用深度表示压力。由此我们可以得到每一层dbar 下的流速方向及大小，具体如图9所示。

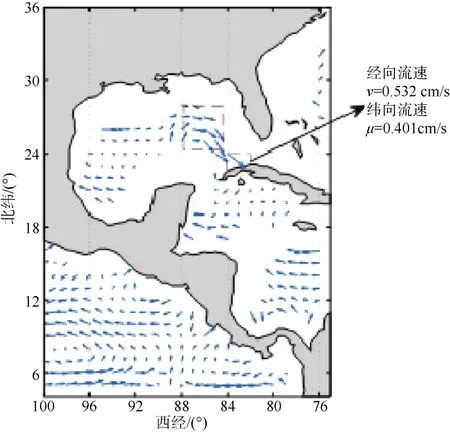
图9 墨西哥湾流场示意图（10 dBar）Fig.9 Diagram of flow field in Gulf of Mexico（10 dBar）

4 结束语

本文对墨西哥湾实测数据展开研究，详细说明了IES 传播时间数据处理方法的质量负载变化、季节干扰去除、时间转化与校正流程。本文还使用第二参考面来降低因温盐剖面实测数据较少而带来的拟合误差。此外，本文对IES 数据与GEM 方法的联合反演方法进行了介绍，最后结合物理海洋学理论对流场的计算进行了简要描述。

由此可知，海洋动力参数反演是海洋科学研究重要的组成部分，对于海洋环境要素监测、海洋灾害预警预报、海上应急救援等具有重要意义。海洋大数据体量大、覆盖广、时序长，但对于复杂时空过程的表征往往是不完备的，主要体现在数据表征不完备、特征表征不完备以及过程表征不完备这3个方面，这对传统数学统计分析和经验反演方法提出了巨大的挑战。对于本文中提到的流场计算，由于我们选取的零流面是针对于2 000 m的深海海底，得到的流速是相对零流面的流速，下一步可以通过加入CPIES 携带的海底流速信息对其进行修正。