基于通道注意特征融合的轴承故障诊断方法

齐爱玲，马森哲

（西安科技大学 计算机科学与技术学院，西安 710699）

0 引言

滚动轴承作为旋转机械的基本部件之一，应用范围极其广泛，而轴承部件的意外失效会带来严重的经济损失和安全问题[1]。因此，实现快速、准确的滚动轴承故障诊断具有重大意义。

近年来，已有大量针对滚动轴承故障诊断的研究[2-3]，其中有效的轴承健康状态识别是故障诊断的关键内容。在故障信号特征提取上，常用的方法有经验模态分解（EMD）[4]、小波分析[5]和变分模态分解（VMD）[6]等。传统信号处理方法虽然能取得较好效果，但是难以处理高度复杂的非线性信号，无法有效处理工业数据。而现有的基于机器学习（ML）[7]的故障诊断方法，如支持向量机（SVM）[8]、梯度提升决策树（GBDT）[9]和K 近邻（KNN）[10]等，往往需要依赖一些带标注的训练数据，且肤浅的机器学习不能准确捕捉特征数据与健康状况之间的复杂对应关系。

随着人工智能技术的发展，基于深度学习的故障诊断方法备受关注，尤其是基于数据驱动的方法，能够快速有效地处理机械信号、获得可靠的故障检测结果，且不必依赖太多的先验专家知识。深度学习模型中，卷积神经网络（CNN）以其自适应特征提取的能力而得到较多应用研究。文献[11]中利用重采样技术将去噪后的时域信号转换为角域信号，并通过Hilbert 变换得到角域信号的包络谱，将3 种信号融合成红绿蓝图像形式以增强样本特征；然后将红绿蓝图像作为改进的ShuffleNet V2的输入样本进行特征提取；最后在ShuffleNet V2的分支进行拼接操作之后放置挤压块和激励块以增强识别准确性，并将校正的线性单元激活函数替换为HardSwish 激活函数以避免坏死。该方法能够有效提高故障识别准确率，并保证模型大小不显著增加。刘昕宇等将去噪处理后的原始振动信号转化为SDP 图像，并作为样本输入到MobilenetV2 模型中自适应地提取故障特征和分类，完成了机械设备的故障诊断[12]。蒋富康等利用自适应噪声完备集合经验模态分解算法对原始振动信号进行预处理，再将预处理后的样本输入到CNN 内嵌长短期记忆（LSTM）神经网络的滚动轴承故障诊断模型中[13]。该故障诊断方法具有更快的拟合速度和更高的准确率。文献[14]中利用连续小波变换将原始的一维时间序列信号转换为二维时频图像，得到适合于二维CNN 的输入数据；并采用数据扩充技术对已标注的故障数据进行扩充；将生成的和原始的故障数据作为训练样本，训练基于神经网络的故障诊断模型，实现滚动轴承故障诊断。Liang 等采用小波变换对一维原始时域信号进行预处理，获得相应的时频图，然后利用建立的CNN 模型完成旋转机械的故障检测，结果表明该方法在测试精度方面的稳定性相当出色[15]。虽然以上将原始信号预处理为二维图像的方法的诊断识别结果相比于直接提取原始信号中故障特征的更加精确，但它们都是采用单域信号进行特征提取，只考虑了数据单域局部信息而忽略了其他更重要的信息特征。

针对传统故障诊断方法通常依赖单域信息输入，导致信号中的部分信息丢失或信息不完整使用的问题，本文提出一种基于通道注意特征融合的轴承故障诊断方法：首先，采用快速傅里叶变换（FFT）和连续小波变换（CWT）同时处理原始振动信号，得到频域信号和时频图像，通过提取多域故障信息特征来提高模型的鲁棒性；然后，将2 种不同域的信息作为双流GM 神经网络（DFGMNet）算法的样本输入，结合多有效通道注意力（MECA）进行通道加权，以增强关键特征提取能力，实现对故障信号的准确分类；最后，在美国的凯斯西储大学、中国的江南大学和加拿大的渥太华大学的轴承故障数据集上验证本文所提故障诊断方法的通用性和有效性。

1 理论基础

在旋转机械故障诊断中，信号处理技术不仅适用于传统的故障诊断，而且适用于基于深度学习和数据驱动的故障诊断。FFT 和CWT 是目前广泛用于旋转机械故障诊断的信号处理方法。

1.1 快速傅里叶变换（FFT）

FFT 是一种基于离散傅里叶变换（DFT）的、能够将时域信号转换为频域信号的方法，具有较低的计算复杂度，因此其计算速度比DFT 快[16]。DFT函数的定义为

式中Xk是序列xn的DFT。考虑旋转机械故障信号的特点，通常会将振动信号转换为频域信号进行进一步分析[17]。

1.2 连续小波变换（CWT）

CWT 是一种时频分析方法。与FFT 不同，CWT可以将一维振动信号转换为二维信号。CWT 时频图像是使用连续小波变换获得的信号能量密度的时频表达。因为Morlet 小波的形状类似于在机械故障中出现的脉冲特征，所以连续小波变换将原始信号分解为时间尺度信号，由Morlet 小波作为母小波通过缩放和转换操作表示[18]。

假设输入信号为x(t)，通过用Morlet 小波缩放x(t)来获得CWT，即

式中：a为小波平移；b为小波尺度；x(t)为任意有限能量信号；ψ(t)为母小波函数。为了在有限的空间中提取更多的时频信息，母小波被用于生成子小波，

通过对信号x(t)执行CWT，将原始的一维时间序列投影到二维时间尺度平面上，再根据尺度与频率的对应关系得到反映信号频率分量随时间变化的时频图像。

1.3 Ghost Module

Ghost Module（GM）[19]将传统的卷积过程分为3 个步骤：首先获得预期数量一半的特征图；然后对所获得的特征图进一步提取与深度卷积；最后将提取的特征拼接起来作为GM 的输出。与卷积相比，GM 通过使用更少的线性运算来获得更丰富的特征信息，可以达到更好的效果。

根据诊断要求，对提取二维特征的GM 模型进行改进，用于一维数据的特征提取，即令

式中：f为卷积操作；b为偏置项；X∈Rh×w×c为输入图像，其中，c为输入通道的数量，h和w分别为输入特征图的高度和宽度；Y∈Rh′×w′×n为输出特征图，其中，n为输出通道的数量，hʹ和wʹ分别为输出特征图的高度和宽度。

然后对Y∈Rh′×w′×n进行线性变换。本文使用3×3 的通道卷积对特征图进行线性运算，得到其余特征图

式中：φi,j为3×3 卷积核的第j次线性运算最终生成的特征图；Yi为Y∈Rh′×w′×n的第i个特征图。

最后将固有特征图和其余特征图级联以获得输出特征图。GM 的实现过程如图1 所示。

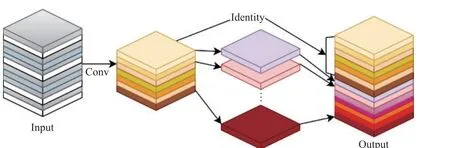
图1 GM 的实现过程Fig.1 Realization process of GM

1.4 通道注意力机制

注意力机制[20]可以根据目标的重要性分配权重，以突出某些重要特征，有效捕捉上下文信息。在故障诊断领域，注意力机制的实质是计算注意力的概率分布。在关注关键分类信息的同时，必须整合其他信息，以消除非敏感信息的影响[21]。在计算机视觉领域，信道注意力机制被引入到卷积块中，为网络性能改善提供了潜力。胡洁等提出了基于挤压和激励思想的挤压-激励网络（SE-Net），它由每个特征映射的全部信息的挤压操作和衡量每个特征重要性的激励操作组合而形成挤压和激励块[22]。在应用SE-Net 时，避免降维对于训练信道注意力尤为重要。相较于参数增加，该模型在提升性能的同时保持了模型的复杂度且计算负担不会增加。文献[23]中提出了一种高效的信道注意力网络（ECA-Net），在提高现有基于自注意力的CNN 模型性能的同时，避免了模型复杂度过高的问题。ECA-Net 成功解决了性能和复杂度的平衡问题，且采用少量参数表现出明显的性能改善效果。ECANet 通过有效的一维卷积进行局部跨通道交互而不降维的方法可分为3 个步骤：1）对特征图进行全局平均池化，得到1×1×C特征向量，其中C为信道维度；2）利用卷积核为1×k的一维卷积计算得到特征向量的重要性预测；3）利用Sigmoid 函数对重要性预测进行0～1 范围的正则化。ECA 模块的实现过程如图2 所示，其中：σ为Sigmoid 函数；k经由C的映射自适应地确定，

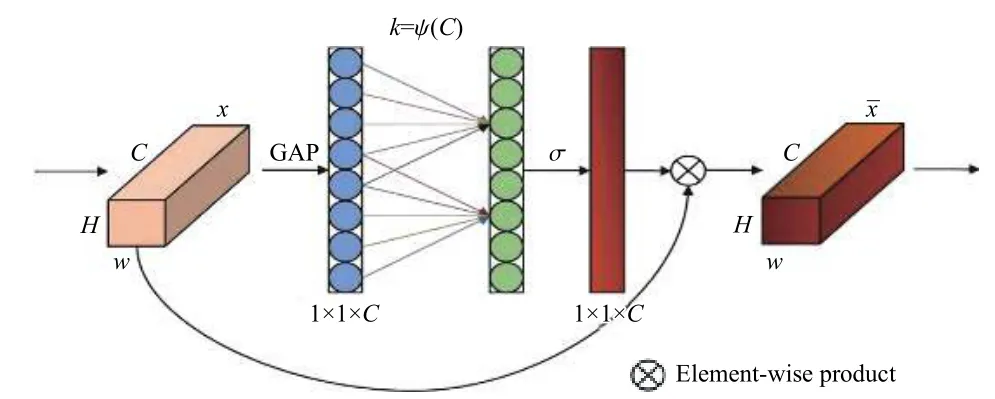
图2 ECA 模块的实现过程Fig.2 Realization process of ECA module

式中： |t|odd为距t最近的奇数；γ和b为常数，本文中分别设置为2 和1。

本文在ECA 模块的基础上提出多有效通道注意力（MECA）模块。MECA 模块通过最大池化过程从特征图中提取纹理特征等细节信息，平均池化提取特征图中与目标相关的背景特征。MECA 模块的实现过程如图3 所示：先对输入的特征图进行平均和最大池化处理，再对处理后的2 个通道的特征图执行拼接操作，其计算过程表达式分别为：

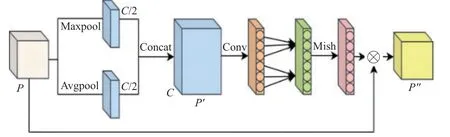
图3 MECA 模块的实现过程Fig.3 Realization process of MECA module

式(7)～式(9)中：P为输入的特征图；Pʹ为池化及拼接操作后的特征图；AvgPool 和MaxPool 分别为平均池化和最大池化操作；cat 为拼接操作；ωc为可学习权重；ASK 为自适应选择的k的一维卷积；P″为输出特征图； ⊗为特征图按位相乘操作。

2 基于通道注意特征融合的轴承故障诊断算法

2.1 DFGMNet 算法基本结构

本文结合FFT、CWT、GM 和通道注意力机制提出双流GM 神经网络（DFGMNet）算法，其整体结构如图4 所示。

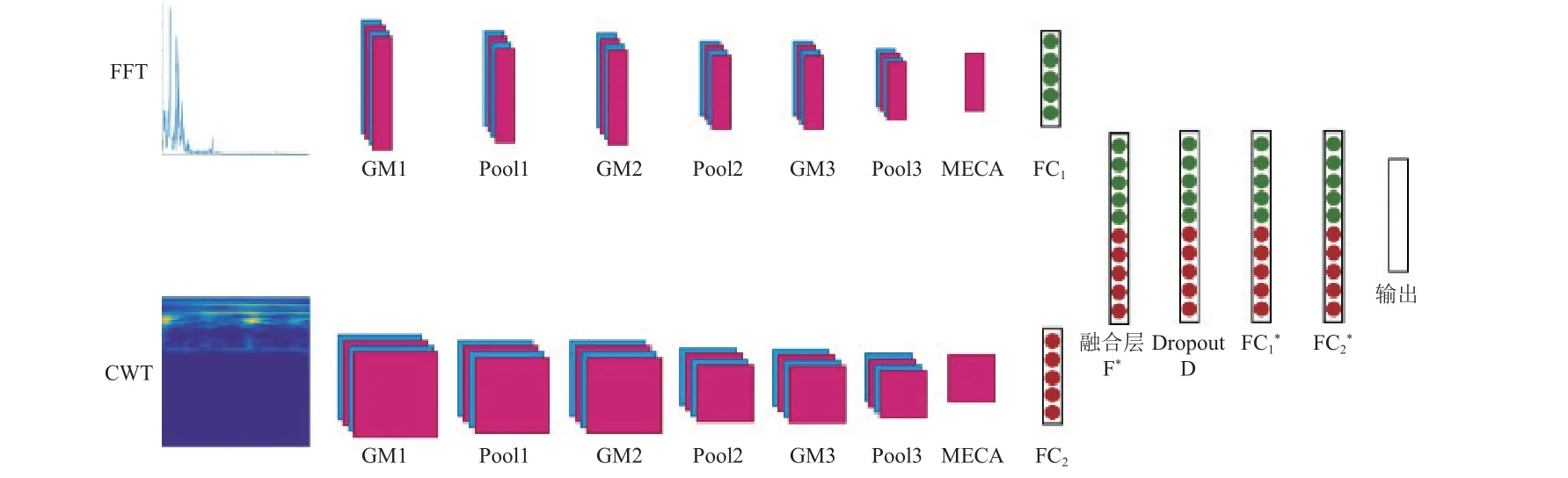
图4 DFGMNet 故障诊断算法Fig.4 Fault diagnosis algorithm of DFGMNet

由图4 可以看到，DFGMNet 故障诊断算法包括基于FFT 频谱的一维GM 结构和基于CWT 时频图像的二维GM 结构，一维和二维DFGMNet 结构均含有3 个GM、3 个池化层（Pool）、1 个MECA模块和1 个全连接层（FC）。故障诊断时，采用一维和二维GM 结构并行进行特征提取，这样可以充分利用样本故障信息，实现故障信息相互补充；在DFGMNet 算法中加入多有效通道注意力（MECA）机制，可以从不同角度提取更具鉴别力的特征，即通过赋予不同通道或区域不同的权重，灵活地捕捉全局和局部的关系，对关键特征区域分配更多的注意力，减少对噪声区域的注意力，从而实现关键特征的增强和噪声干扰的降低，增强算法的鲁棒性，提高算法的分类准确率。将2 个GM 结构的全连接层FC1和FC2提取的特征通过融合层F*进行拼接，最后在F*和FC1*之间引入Dropout[24]使部分神经元以一定的概率暂停工作，转而学习更加具有鲁棒性的信息，以提高算法的泛化能力，抑制过拟合。

2.2 故障诊断过程

故障诊断过程可分为4 步：

1）首先对原始采样数据同时进行FFT 和CWT预处理，得到频谱图和时频图；

2）将频谱图和时频图输入DFGMNet 故障诊断算法提取信号的频域和时频域特征，结合MECA机制进行通道加权，通过特征融合层得到组合故障特征；

3）将DFGMNet 算法用于组合故障特征的监督学习，并对算法中的权重和参数进行训练和更新；

4）通过3 个故障数据集验证DFGMNet 算法的故障分类性能。

3 实验及结果分析

3.1 实验设置

3.1.1 数据集

采用凯斯西储大学（CWRU）、江南大学（JNU）和渥太华大学（OTTAWA）的轴承故障数据集来验证DFGMNet 故障诊断算法的性能。

对于CWRU 的数据集，本文选用12 kHz 的驱动端采集的故障数据，轴承转速为1772 r/min。该数据集包括滚动体、内圈和外圈3 种故障状态，以及1 种正常（无故障）轴承数据；每种故障状态含3 种故障直径（0.007、0.014 和0.021 inch），共9 种轴承故障数据（如表1 所示）；每种故障状态生成200 个样本，并按8:2 划分为训练集和测试集。

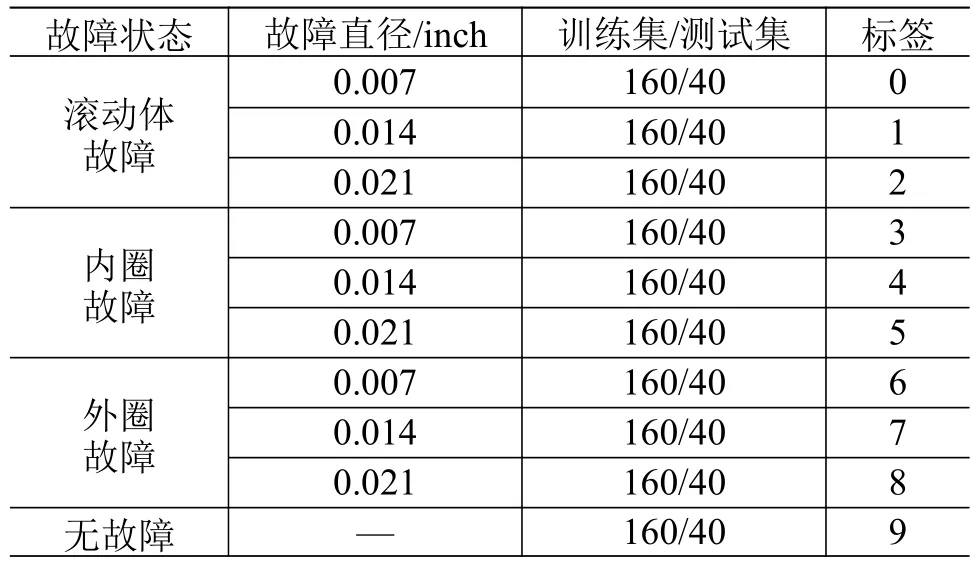
表1 CWRU 实验数据Table 1 CWRU experimental data

JNU 的数据集采样频率为50 kHz，故障状态包括外圈、内圈和滚动体故障。本文使用转速600 r/min的轴承数据作为实验数据集，加上正常（无故障）工况共4 种状态（如表2 所示）。

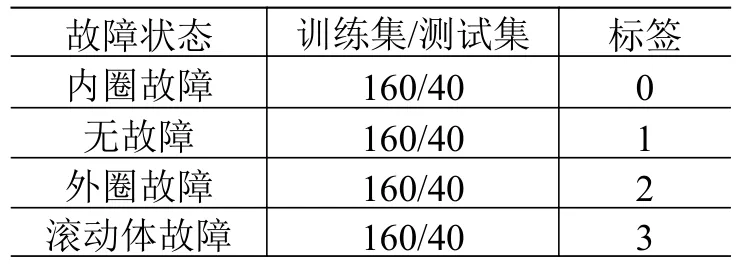
表2 JNU 实验数据Table 2 JNU experimental data

OTTAWA 的数据集包含了滚动轴承不同故障类型的振动和转速数据。本文使用减速工况下的故障数据，包括内圈、外圈、球和复合4 种故障状态，以及1 种正常（无故障）轴承数据（如表3 所示）。

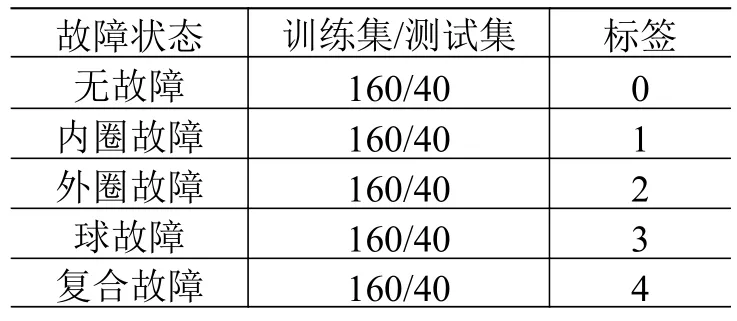
表3 OTTAWA 实验数据Table 3 OTTAWA experimental data

3.1.2 实验超参数设置

本文实验在Pytorch 的框架下进行验证，对原始振动数据采用长度为1024 的采样方式进行随机分割，使用Adam 优化器优化训练DFGMNet 算法，应用交叉熵损失函数作为该算法的损失度量函数，实验参数设置如下：学习率初始化为0.001；模型中的dropout 参数为0.2；训练时期的总数为50；由于批量大小（Batch S）参数会对实验结果产生一定的影响，所以将批量大小分别设置为16、32、64、128，由图5 可知批量大小为16 时的故障诊断准确率最高。所有实验均进行10 次，以降低测试过程中的偶然性，并将平均值作为最终分类结果进行分析。

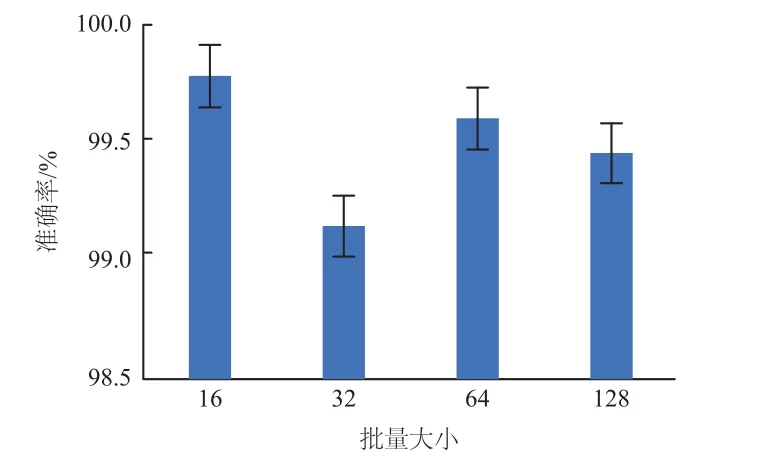
图5 CWRU 批量大小对诊断准确率的影响Fig.5 Effect of CWRU batch size on diagnostic accuracy

3.2 诊断结果及对比实验

使用上述3 个轴承故障数据集验证基于通道注意特征融合的轴承故障诊断方法的通用性和有效性。为验证频域和时频域作为DFGMNet 算法的输入数据的样本特征提取效果，以本文DFGMNet框架为基础，对不同的通道数和输入数据进行对比实验。构建5 种算法进行轴承故障诊断的对比实验，其中：Model1、Model2 和Model3 为采用单通道的算法；Model4 和Model5 为采用双通道的算法（Model5 为本文所提算法）。各算法的框架及输入数据如表4 所示。

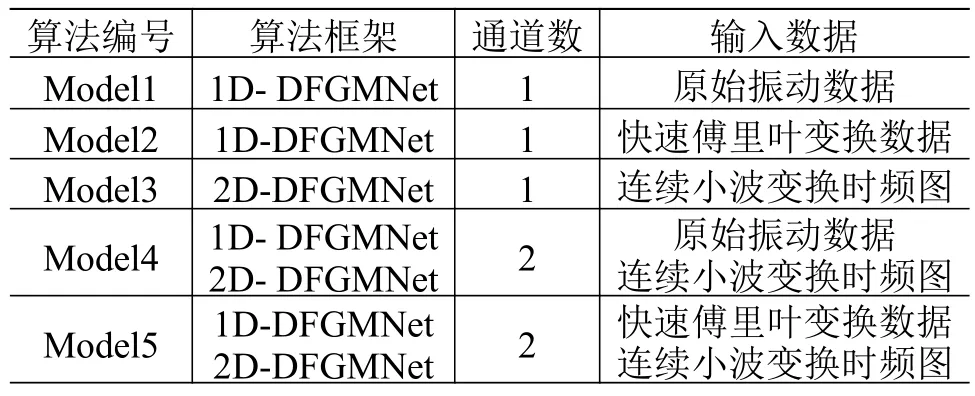
表4 5 种算法的框架及实验输入数据类型Table 4 The framework and the type of input data of five algorithms

本文实验以准确率作为各算法的分类性能的评价指标，它是指正确预测类别样本的数量占总样本数量的百分比。表4 提到的5 种算法的实验对比结果如表5 所示。

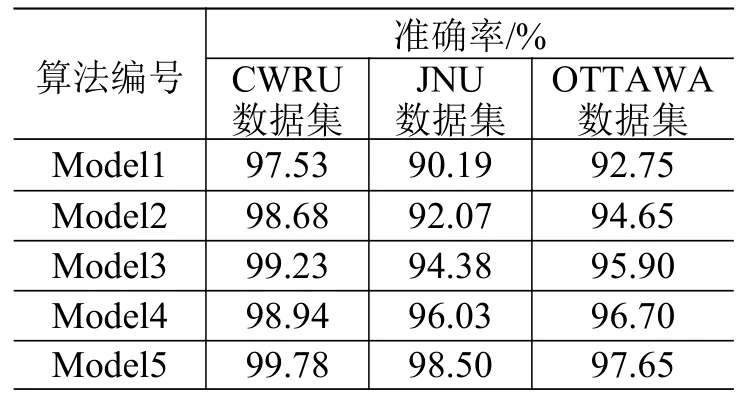
表5 5 种不同框架的算法的实验结果对比Table 5 Experimental result comparison of five algorithms with different frameworks

结合表4 和表5 可以看出：1）Model1 的输入数据为原始振动数据，在3 个测试集上的准确率分别为97.53%、90.19%和92.75%；2）Model2 的输入数据为快速傅里叶变换数据，在3 个测试集上的准确率分别为98.68%、92.07%和94.65%，与Model1 的相比分别提高了1.15、1.88 和1.90 个百分点；3）Model3的输入数据为连续小波变换时频图，在3 个测试集上的准确率分别为99.23%、94.38%和95.90%，与Model2 的相比分别提高了0.55、2.31 和1.25 个百分点；4）Model4 和Model5 均采用DFGMNet 故障诊断算法，Model4 的输入数据分别为原始振动数据和连续小波变换时频图，在3 个测试集上的准确率分别为98.94%、96.03%和96.70%；Model5 的输入数据分别为快速傅里叶变换频域数据和连续小波变换时频图数据，在3 个测试集上的准确率分别为99.78%、98.50%和97.65%；Model5 与Model4相比，准确率分别提高了0.84、2.47 和0.95 个百分点。由此可知，本文提出的双流GM 神经网络故障诊断算法将频域和时频图作为样本输入可达到最佳的特征提取效果。

3.3 三个数据集下的故障诊断结果

首先，对CWRU 数据集每个类别随机构造200 个样本，构成一个包含2000 个样本的样本集；然后使用t-distributed 随机邻居嵌入（t-SNE）方法[25]，将该数据集所有类别的数据在本文提出的DFGMNet 故障诊断算法中作为原始输入信号，测试数据集在全连接层FC1、FC2和FC1*的学习过程中映射数据的二维特征。由图6(a)可见，CWRU 原始数据特征相对分散并且难以区分。由图6(b)和图6(c)可见，与原始输入数据相比，经GM 和池化操作后，每类样本逐渐聚类，且在全连接层FC2中特征的聚类比在FC1中的更好。由图6(d)可见，CWRU 数据集中同一类的特征非常集中；且与FC1和FC2中的特征映射结果相比，FC1*中不同类特征分布之间的距离最大。结果表明，采用本文所提双流GM 神经网络模型的分类器可轻松完成数据集各自样本间的分类，得出较优的分类结果。

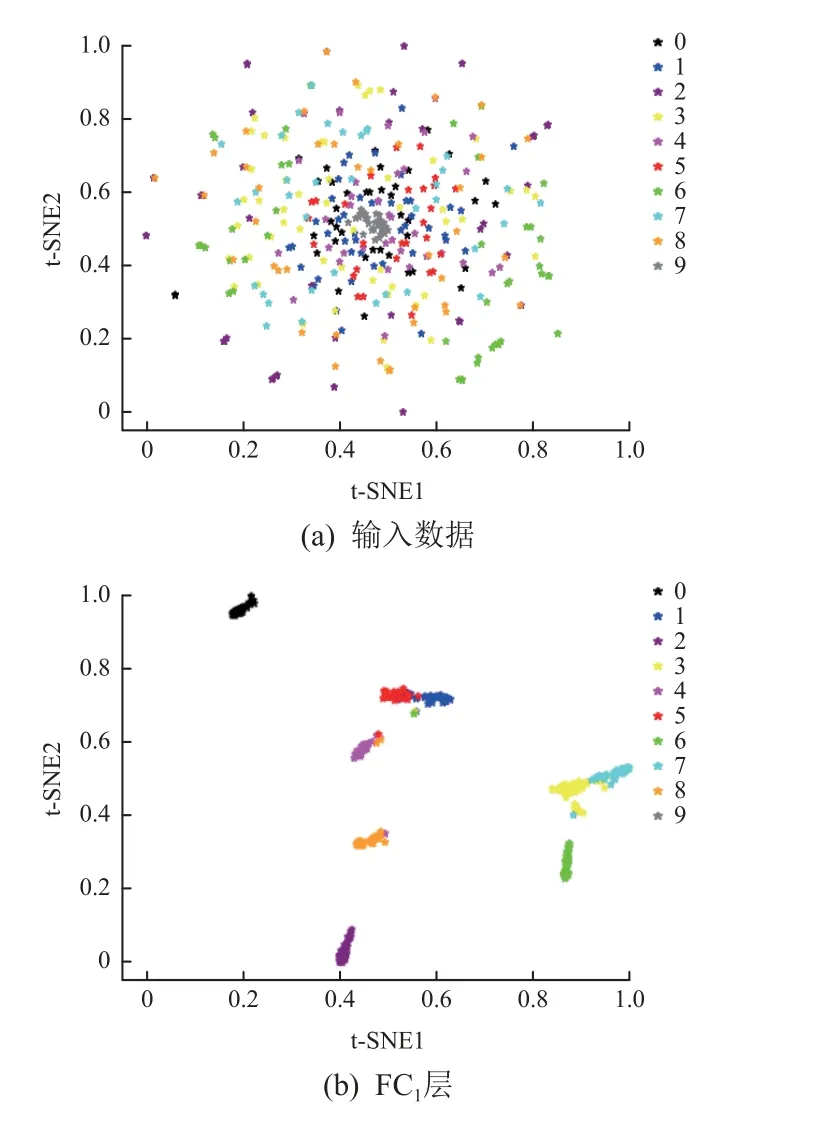
图6 输入数据以及全连接层FC1、FC2、FC1*的特征可视化Fig.6 Feature visualization of the input data and the fully connected layers of FC1, FC2 and FC1*

3.4 不同方法对比

为进一步验证本文所提故障诊断方法的分类精度，对比分析了本文所提DFGMNet 算法和目前主流的4 种算法在3 个数据集上取得的分类准确率，结果如表6 所示。可以看到，本文所提算法对CWRU、JNU 及OTTAWA 数据集的分类准确率分别达到99.78%、98.50%及97.65%，均略高于目前主流的4 种算法。这表明：本文算法能够有效降低振动信号噪声对故障诊断识别的干扰，提取更具鲁棒性的特征，从而提高算法的分类性能；本文算法采用的超参数相对达到最优值，有效提高了滚动轴承的故障诊断准确率。

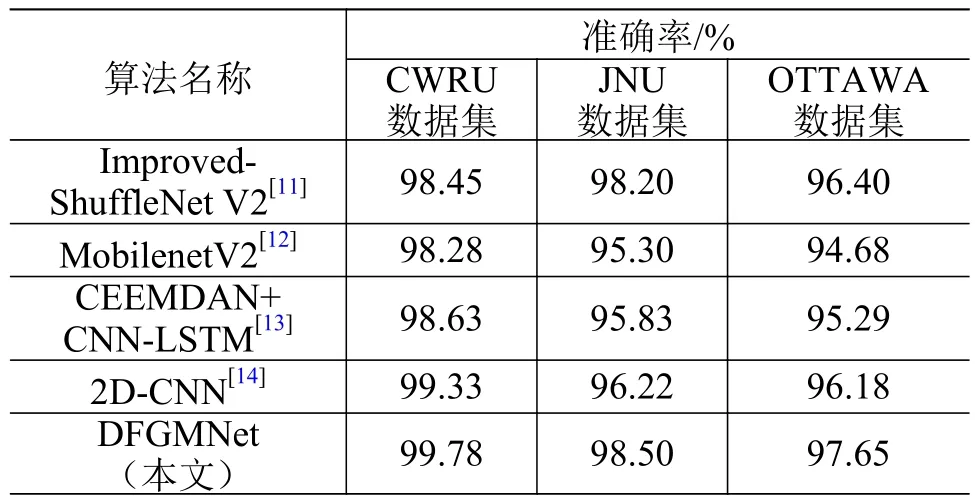
表6 不同算法的分类准确率对比Table 6 Classification accuracy comparison among different algorithms

4 结束语

针对现有的深度学习法通常依赖单域信息输入而导致信号中部分信息丢失或信息的不完整使用的问题，本文提出一种基于通道注意特征融合的轴承故障诊断方法。该方法采用DFGMNet 算法，能够自适应提取信号的频域和时频域特征，并通过引入通道注意力机制克服了传统算法的局限；还在CWRU、JNU 和OTTAWA 轴承故障数据集上展现出更高的分类准确率，为故障诊断领域带来了显著的创新和性能提升。该方法有望在将来成为工业实践中故障诊断的有力工具，为提高滚动轴承故障诊断的准确性和可靠性提供有力支持。