航天器多级自由边界模拟系统姿态平衡协调控制

张大志，骆 巍，刘 闯，朱万铖*

（1.北京科技大学 机械工程学院，北京 100083； 2.北京卫星环境工程研究所，北京 100094）

0 引言

光学观测航天器的发展趋势是高精度、高稳定性。然而，由于推进器工作、结构机构动作以及人员活动等客观因素引起的航天器微振动对观测精度的影响日益突出[1]。为了验证在微振动条件下航天器各部分（平台-隔振器-载荷）之间的振动传递特性，需要在地面开展航天器在轨微振动环境模拟试验。其中，自由边界模拟系统作为关键设备，可以实现沿重力矢量方向的低刚度重力卸载，从而抵消航天器自身重力的影响，同时建立低频自由边界条件，消除天地力学环境不一致对航天器地面微振动测试精度和在轨成像质量测试的影响，为航天器地面微振动试验提供基础测试条件[1]。

目前，地面自由边界系统模拟零重力环境主要通过被动或主动控制的机械悬吊/支撑结构实现。法国的SPOT4 卫星通过4 根弹性吊带与整星吊具相连，辅助配备自动调平机构，实现6 点刚性模态频率低于1 Hz[2]；日本的OICETS 激光通信卫星在地面测试阶段同样采用悬吊装置进行重力卸载[3]；美国的SDO 卫星在微振动试验过程中，在整星底部采用低频气囊支撑，模拟自由边界条件的同时隔绝环境振动[4]。国内在航天器微振动试验技术研究中，张庆君等在2010 年采用柔性吊索悬吊装置对敏感载荷单机进行了局部重力卸载，开展微振动试验[5]；王光远等在2012 年采用低频支撑装置实现对某光学遥感卫星自由边界条件的模拟，实施了整星的微振动试验[6]；庞世伟等在2016 年通过弹性悬挂装置完成了某型号卫星多级多层次自由边界模拟和微振动试验[7]。这些弹簧-钢索悬吊装置、气囊支撑装置和弹簧支撑装置等机械装置结构紧凑、可控性好、制造和维护方便且成本低，能在各个运动方向提供零重力环境状态。然而随着航天技术的进步和航天任务的多样化，对于航天器多部分复合试验，单一的悬吊/支撑系统无法实现航天器的自由边界条件环境模拟[8-9]；此外，目前使用的自由边界模拟装置主要通过平衡配重或手动拉伸/压缩弹性装置来实现重力卸载，耗时又费力。因此，有必要开展多级自由边界模拟系统自动化技术研究。另外，由于航天器整体结构和各部分结构质量偏心问题的存在，重力卸载过程中需要对自由边界模拟系统进行平衡协调控制。

本文就此开展航天器多级自由边界模拟系统自动化技术和平衡协调控制技术研究，主要内容包括航天器悬吊/支撑自由边界模拟系统自动装置的研制、重力卸载过程姿态平衡协调控制算法的设计和实现。

1 自由边界模拟系统设计

基于航天器多部分复合试验的现实需要，分别针对航天器设施和平台部分的重力卸载，研制了顶部悬吊式自由边界模拟子系统和底部支撑式自由边界模拟子系统，并通过研制自由边界模拟系统控制模块对重力卸载时的航天器姿态平衡协调进行控制。为便于描述，后文中以平衡协调控制指代重力卸载时的航天器姿态平衡协调控制。

1.1 顶部悬吊式自由边界模拟子系统

顶部悬吊式自由边界模拟子系统的功能是实现航天器设施的低刚度重力卸载，通过多点垂直吊起航天器载荷，使其处于零重力状态。悬吊式自由边界模拟装置结构如图1 所示，主要由悬吊驱动模组、钢丝绳-弹簧以及传感器等组成。

图1 悬吊式自由边界模拟装置结构组成示意Fig.1 Schematic of suspension-type free boundary simulation device structure

悬吊驱动模组由电机-减速器、直线导轨、丝杠、滑块、手动联轴器及力传感器连接件等组成。丝杠运动组件驱动滑块运动，通过钢丝绳和滑轮组拉动弹簧，弹簧通过钢丝绳连接载荷实现最终的重力卸载。同时，通过对拉力信号，设施纵向、切向、径向3 个方向的位移，以及设施与平台之间的相对位置监测，实现重力卸载过程中的自动调节和航天器设施平衡协调控制。悬吊驱动模组的优点包括：行程可适应低刚度弹簧的大伸长量变化；对钢丝绳的作用为纯拉伸，无扭转；具备实现电动/手动切换的功能；滑块位置监测能实现大行程、精细调节等。

顶部悬吊式自由边界模拟子系统的工作原理为：电机-丝杠运动组件驱动滑块沿导轨做直线运动，通过钢丝绳与导向滑轮组拉动低刚度弹簧变形，最终由末端的自由端工装连接载荷设施实现重力卸载。另外，滑轮组两端的限位保护块和限位姿态调整组件在重力卸载和位置调整过程中提供上下连接界面的双重限位保护。通过对拉力信号，卫星与限位姿态调整组件之间的相对位置，以及卫星设施与航天器平台之间的相对位置监测，实现重力卸载过程中的平衡协调控制。

该方案可有效避免卸载对象垂直与水平运动的耦合，降低设施就位、对中的难度；采用滑轮组的钢丝绳-弹簧折回形式，有效降低了悬吊结构的高度，同时便于人工调节；对设施各方向进行位移监测，通过位移闭环控制确保试验对象在整个调整过程中的姿态位置始终处于合理范围内。

1.2 底部支撑式自由边界模拟子系统

底部支撑式自由边界模拟子系统的功能是实现航天器平台的低刚度重力卸载，由多台支撑式自由边界模拟装置和一组上下安装板构成。底部支撑式自由边界模拟装置结构如图2 所示，主要工作机构为支撑驱动模组和弹簧。

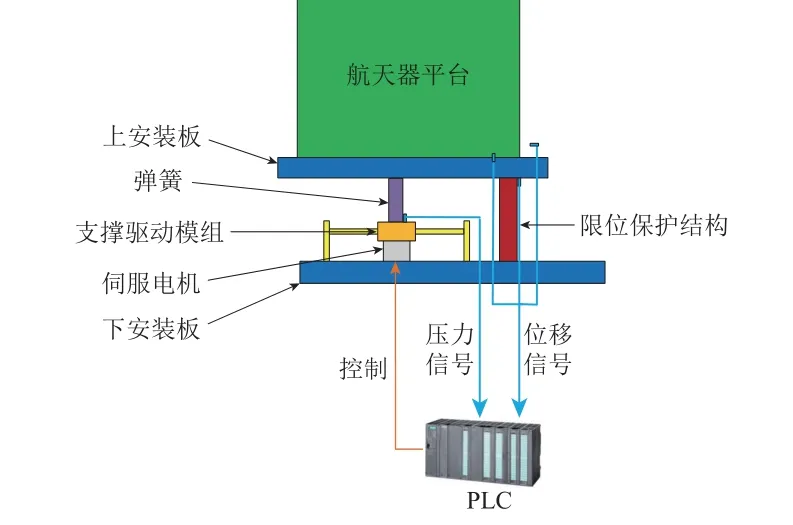
图2 底部支撑式自由边界模拟装置结构组成示意Fig.2 Diagram of bottom-supported free boundary simulation device structure

底部支撑式自由边界模拟装置通过上下安装板连接卸载对象和支撑弹簧，由伺服电机-丝杠直线运动驱动模组压缩底部弹簧变形，实现航天器平台的重力卸载。同时，通过力传感器采集监测弹簧支撑力数值，实现重力卸载的自动闭环控制；通过电涡流位移传感器对航天器平台与工装之间纵向、切向、径向3 个方向的相对位置进行高精度监测，完成航天器平台的平衡协调控制。另外，由限位保护结构在航天器重力卸载和位置调整过程中提供上下安装板之间的限位保护。

该设计方案的核心特点为：可以有效避免卸载对象垂直与水平运动的耦合，降低航天器平台就位、对中的难度；将支撑弹簧、限位姿态调整装置和丝杆驱动装置进行模块化集成，便于适应航天器平台在不同条件下的卸载需求；具备多方向位移监测，通过位移闭环控制确保试验对象在整个调整过程中的姿态位置始终处于合理范围内。

1.3 自由边界模拟系统控制模块

1.3.1 模块的组成

根据硬件的作用将控制模块分为4 层——管理层、控制层、驱动执行层和现场仪表层。控制模块的硬件组态如图3 所示。

1）管理层：由工控机及配套设备（如打印机等）组成，主要用于控制模块的软件集成、程序编写和HMI（人机界面）监控。

2）控制层：PLC 控制系统选用西门子CPU S7-300 作为主控制器；I/O 模块的作用是接收操作台信号和现场仪表层传感器信号，并将CPU 按照程序逻辑处理后的控制指令输出到驱动执行层，控制电机运转。软硬件之间采用专用的ProfiNet 通信方式，控制层PLC 与驱动执行层的伺服控制单元之间采用工业领域通用的Modbus 通信协议[10]。

3）驱动执行层：由伺服控制单元、伺服驱动器以及伺服电机组成。伺服控制单元的作用是将控制层PLC 输出的指令转换成伺服电机驱动器的控制信号，伺服控制单元与伺服驱动器之间采用CAN通信协议。在多电机控制系统中，CAN 通信协议可以保证每一套伺服电机驱动器接收和发送信号的准确性和稳定性，从而保证整套控制模块的控制性能。伺服电机是自由边界模拟系统控制模块的主要执行机构，具有响应快、效率高和输出转矩平稳等特点[11]。

4）现场仪表层：由传感器组成，力传感器和位移传感器用于构成反馈闭环，激光位移传感器用于监测航天器设施和平台的相对位置，绝对值编码器用于监测丝杠直线运动组件的位移量。现场仪表信号输入到控制层中用于逻辑处理。

1.3.2 模块的工作原理

在航天器设施和平台的重力卸载过程中，主要的执行机构是电机，同时通过弹簧力的监测和航天器位置的监测完成闭环控制。自由边界模拟系统控制模块的工作原理如图4 所示，监测弹簧力和航天器位置的传感器信号采集到PLC 中，与上位机的设定值进行比较和逻辑运算；再由PLC 将控制信号输出到伺服驱动器驱动伺服电机；然后通过丝杠直线运动组件和弹簧施加力，实现航天器设施和平台的重力卸载和纵向位移。

图4 自由边界模拟系统控制模块工作原理Fig.4 Working principle of the free boundary simulation system control module

伺服驱动的控制原理如图5[12]所示，电流环作为最内环，其作用是控制电机转矩，对系统响应的快速性与准确性有重要影响；速度环的作用是使电机转速更平稳和更快地达到期望值，同时降低扰动对系统的影响，从而减小转速波动；最外环为位置环，其作用是通过检测的实际位置信号与期望位置信号的差值输出速度环参考指令，从而控制电机按照设定的速度和方向旋转，进而控制电机的转动角度。

图5 伺服驱动的控制原理[12]Fig.5 Control principle of a servo drive [12]

本次设计的自由边界模拟系统控制模块所使用的某型号伺服电机3 个闭环的控制精度如表1 所示。

表1 某型号伺服电机驱动控制参数Table 1 Control parameters of a servo motor drive

2 自由边界模拟系统平衡协调控制策略的设计

如1.3 节所述，自由边界模拟系统控制模块的工作原理是通过伺服电机驱动丝杠直线运动组件使弹簧发生变形，实现航天器顶部设施和底部平台的重力卸载和纵向位移控制。这一过程分别由自动控制模式下的力闭环和位移闭环完成。由于航天器设施和平台的结构及布置存在非对称性，其各自和整体的质心均存在一定的偏心现象。为确保卸载过程中航天器设施和平台不发生翻转和旋转，且卸载后两者自身角度和相对位置关系与在轨状态保持一致，需要在卸载过程中设计有效的平衡协调控制策略。

2.1 多点卸载状态力协调控制策略设计

2.1.1 力闭环控制模型的建立

航天器重力卸载过程采用力闭环控制，控制系统的设定目标值为卸载施力点的重力，力传感器测量弹簧变形输出的力作为反馈值。力闭环控制系统组成如图6 所示。

图6 力闭环控制系统组成Fig.6 Block diagram of the force closed-loop control system

伺服电机位置环的数学模型表达式为

式中：θ为丝杠直线运动模组的输入转动角度，°；θ*为控制器的输出转动角度，°；K1为伺服电机比例系数；J为伺服电机转动惯量；B为伺服电机运动阻尼系数。

丝杠直线运动模组中包括减速器、联轴器、齿轮以及滚珠丝杠等机械结构，模组的输入转动角度θ与输出直线位移L之间的关系表达式为

式中K2为丝杠直线运动模组比例系数，m/(°)。

丝杠直线运动模组的输出直线位移L与弹簧的输出力F之间的关系表达式为

式中K3为弹簧刚度系数，N/m。

联立式(1)、(2)、(3)，可得力闭环控制模型的开环传递函数

式中N(s)为PID 控制器传递函数，PID 控制算法的数学表达式为

式中：Kp为比例环节系数；Ki为积分环节系数；Kd为微分环节系数。

式(4)与式(5)联立，可得力闭环控制模型的闭环传递函数

2.1.2 多点卸载力协调控制模型的建立

航天器设施和平台由于非对称结构及布置而导致偏心，且多点重力卸载过程中各点分配力不同，因此存在各点卸载不同步导致试验件发生偏转，引起自由边界模拟装置变形。鉴于航天器重量大、体积大，在自由边界模拟系统的设计过程中，自由边界模拟装置平衡方程的数量超出限制会产生超静定问题。为解决此问题，我们设计了如下卸载力分配模型：

式中：G为试验设备总重量；y为卸载力切向力臂；z为卸载力径向力臂；n为卸载分配点总数。

式(7)中：第1 项为纵向静力平衡方程；第2 项为卸载力对质心的切向力矩平衡方程；第3 项为卸载力对质心的径向力矩平衡方程；第4 项中将8 个卸载点分成4 组，对向分布的2 个卸载点为1 组，每组承担1/4 的航天器平台重力，即这一项中共有4 组方程，但本质上与第1 项是重合的。因此，目前共有6 组平衡方程，可以解出3 次超静定问题；可通过式(7)第5 项的多次迭代优化得到其他不定解的最优解。以某600 kg 试验件为例，其质心坐标为(2000 mm, -100 mm, 20 mm)，其支撑式自由边界模拟子系统8 个支撑点的重力卸载分配如表2 所示。

表2 支撑式自由边界模拟子系统重力卸载分配表Table 2 Gravity unloading allocation of the supported free boundary simulation subsystem

得出各点卸载所需要的平衡力后，为解决偏心导致的各点卸载不同步使航天器发生偏转的问题，在原本力闭环控制模型中加入相邻卸载装置和距离最远点卸载装置反馈力的偏差作为补偿，建立多点卸载力协调控制模型，如图7 所示。

图7 多点卸载力协调控制模型Fig.7 Multi-point unloading coordination control model

2.2 多点卸载状态位移协调控制策略设计

2.2.1 位移闭环控制模型的建立

自由边界模拟系统的拉力/压力与航天器设施/平台的重力平衡之后，需要调整设施及平台自身角度以及两者相对位置，以便与航天器在轨状态保持一致。这一过程通过位移闭环控制系统完成，系统以航天器的纵向位移变化作为反馈信息和控制对象。位移闭环控制系统组成如图8 所示。

图8 位移闭环控制系统组成Fig.8 Block diagram of the displacement closed-loop control system

在航天器重力卸载过程中，伺服电机通过丝杠直线运动模组拉/压弹簧，输出力以平衡航天器的重力，此阶段仅有运动模组中直线运动构件位移变化和弹簧长度变化，而航天器的位置不改变。当弹簧的拉力/压力随着伺服电机转动提升到平衡航天器该点重力的时刻，弹簧长度不再改变，航天器开始产生纵向位移变化。此刻，航天器该点的位置变化可以等效为丝杠直线运动模组输出的纵向直线位移，位移控制器与卸载力控制器一样采用PID 算法。位移闭环控制系统的动态结构如图9 所示。

图9 位移闭环控制系统动态结构Fig.9 Dynamic structural diagram of displacement closedloop control system

2.2.2 多点卸载位移协调控制模型的建立

为解决偏心导致的航天器偏转问题，采用与力卸载过程多点协调控制模型中原理相似的位移补偿方式，在对本点纵向位移监测反馈的同时，结合其他点纵向位移的变化进行偏差耦合[13-14]，对航天器的平衡姿态进行协调控制。多点卸载位移协调控制模型如图10 所示。

图10 多点卸载位移协调控制模型Fig.10 Multi-point unloading displacement coordination control module

3 多点协调控制算法的设计功能实现与现场验证

3.1 自由边界模拟系统控制模块的功能实现

目前使用的自由边界模拟装置主要通过平衡配重或人工拉伸/压缩弹性装置实现重力卸载，而本文研制的自由边界模拟系统控制模块可以实现航天器设施和平台重力卸载的电动控制，在提高卸载效率的同时进一步提高卸载过程中力和位置的控制精度。通过可编程控制器中控制程序的编写和人机界面的设计，可以实现对试验设备的电动操作和对现场仪表信息的获取及监测。图11 为人机界面设计示例。

图11 航天器微振动试验系统人机界面示例Fig.11 Interface example of HMI of spacecraft microvibration test system

自由边界模拟系统控制模块的程序功能实现有手动和自动2 种控制模式。

1）手动控制模式：操作人员手动对伺服电机进行速度设定和启停控制，既可以对单个电机进行控制，也可以对悬吊子系统或支撑子系统全部电机进行同步控制。

2）自动控制模式：自动控制为闭环控制，通过力闭环和位移闭环实现试验设备的重力卸载和纵向位移姿态控制，伺服驱动方式选择精度最高的位置环。目标设定值和反馈值通过PID 算法输出控制电机运转的脉冲值，电机以驱动器位置环设定速度值运转，驱动试验设备到达卸载目标。

3.2 自由边界模拟系统多点卸载协调控制策略的验证

如2.1 节所述，在建立了卸载过程的力闭环控制模型后，为解决偏心导致的偏转问题，在原本力闭环控制模型中加入相邻卸载装置和距离最远点卸载装置反馈力的偏差作为补偿，优化得到多点卸载平衡协调控制模型。为验证优化效果，对比加入力偏差补偿前的力闭环控制模型的力传感器测量曲线（如图12 所示）与加入力偏差补偿后的多点协调控制模型的力传感器测量曲线（如图13 所示）。

图12 力闭环控制模型力传感器测量曲线Fig.12 Measured force sensor curve for force closed-loop control model

图13 多点卸载协调控制模型力传感器测量曲线Fig.13 Measured force sensor curve for multi-point unloading coordination control model

由图12 和图13 比较可以看出，加入相邻卸载装置和对向卸载装置的力偏差补偿之后，在卸载过程中各卸载点的同步效果更好，避免了航天器由于偏心、在起重过程中受力不均而产生的翻转，减小了对自由边界模拟系统限位装置施加的力矩。在实际应用中，需要根据现场控制情况对PID 控制器的参数进行调整，寻找最佳控制效果。

3.3 自由边界模拟系统卸载平衡协调控制策略的验证

通过图10 可以看出，多点卸载平衡协调控制模型增加了本重力卸载施力点的纵向位移与其他施力点纵向位移的差值耦合项作为补偿输入，以达到更好的协调控制效果。将该控制策略引入现场控制程序后，多点姿态平衡协调控制模型的纵向位移传感器测量曲线如图14 所示。

图14 多点姿态平衡协调控制模型各点纵向位移测量曲线Fig.14 Measured vertical displacement curve for multi-point attitude equilibrium coordination control model

由图14 可以看出，加入本卸载装置之外其他卸载装置的纵向位移偏差补偿之后，可以在姿态调整过程中得到更好的控制效果，大幅度缩小了纵向位移不同步引起的周向和径向位移，以及航天器姿态调整过程中的角度倾斜。根据现场验证，系统的弹簧拉/压力控制精度和位置精度均满足设计要求。

4 结束语

本文针对地面在轨微振动环境模拟试验中航天器多部分复合试验的需求，在航天器上、下两端分别建立悬吊式自由边界模拟子系统和支撑式自由边界模拟子系统，设计并建立了以PLC 为控制单元、伺服电机为主要执行机构的自由边界模拟系统控制模块，搭建了可以在安全的地面测试环境下实现航天器重力卸载和自由边界模拟的试验平台。为了解决航天器结构质量偏心导致卸载过程中产生的偏转问题，在基础力闭环控制和位移闭环控制的基础上加入偏差耦合算法，大幅提升了同步控制效果，保证了航天器重力卸载过程中的姿态稳定，实现了在航天器到达指定位置过程中的平衡协调控制，且力闭环控制精度和位置精度满足地面测试环境的需要。

本文为未来航天器地面模拟试验中重力卸载过程中姿态协调控制系统的设计积累了工程经验，下一步拟在控制算法方向上进行更深入研究。