探地雷达正演的间断伽辽金法影响因素分析

冯德山, 刘硕, 王珣*, 丁思元, 张华, 苏玄, 陈磊, 颜照坤

1 中南大学地球科学与信息物理学院, 长沙 410083

2 东华理工大学地球科学学院, 南昌 330032

0 引言

探地雷达(Ground penetrating radar,GPR)是一种利用高频电磁波查明地下界面或者地质体空间位置、结构的勘探方法.由于它操作简单、效率快、结果直观等优点,现已被应用于多个领域,例如：民用基础设施检测、地震灾害生命探测与救援等(刘澜波和钱荣毅,2015;胡群芳等,2020).但因地下介质较为复杂,又存在各种自然干扰和人为噪声,导致雷达剖面各种波形混杂,难以区分.因此需要开展GPR正演模拟,了解雷达波的传播过程和特征,提高探地雷达的解译精度,为逆时偏移和反演奠定理论基础(刘四新和曾昭发,2007;朱尉强和黄清华,2016;葛德彪和魏兵,2019).

探地雷达数值模拟方法很多,包括时域有限差分法(finite-difference time-domain,FDTD)(Yee,1966;李静等,2016)、时域有限单元法(finite element time-domain,FETD)(冯德山和王珣,2017;王洪华等,2018)、时域间断Galerkin算法(discontinuous Galerkin time-domain,DGTD)(König et al.,2010)、时域伪谱法(pseudo spectral time-domain,PSTD)(李展辉等,2009;Huang et al.,2010;Fang and Lin,2012)、有限体积法(finite-volume time-domain,FVTD)(Munz et al.,2000)、辛算法(方宏远和林皋,2013;雷建伟等,2020)等,这些算法各有特色.FDTD算法虽简单易懂,计算速度快,但频散较严重,通常用于直交网格,对于几何不规则的地质体,并不能紧密贴合其边界(葛德彪和闫玉波,2005;李静等,2010).FETD算法能利用非规则的三角形对模拟区域进行剖分,可处理地表起伏问题,但需要求解大型矩阵,计算效率低(冯德山等,2013;Jin,2014;王洪华等,2019).PSTD算法计算精度高,占用内存相对较小,但不适用于复杂的地质体模型,不利于并行计算.FVTD算法本身包含几何信息,易处理复杂网格问题,但算法本身较为复杂,不易提高计算精度.而DGTD算法结合了FETD与FVTD算法的优点,可与非规则网格结合,易于实现网格自适应和并行,计算精度高,受到众多研究学者的青睐(Hesthaven and Warburton,2002).1973年,Reed和Hill(1973)在微分三角形离散坐标方程中提出了DG的思想.Hu等(1999)在二维波动方程的半离散背景下研究了DGTD算法的色散和耗散特性.Lu等(2005)推导了Debye线性色散介质和完全匹配层区域中Maxwell方程的统一公式.Diaz Angulo等(2011)将DGTD算法应用于GPR三维模拟中,并与FDTD算法进行对比.Yang等(2017)采用了非结构化四面体的正交基函数,求解了三维非均匀介质的DGTD迭代公式,说明该算法具有较高的精度和宽频模拟能力.这些论文都证明了DGTD算法具有精度高、收敛性高的优点,表明了DGTD算法在GPR正演模拟中的优势.

随着DGTD算法在计算电磁学领域的深入,很多学者也对DGTD算法进行了各种改进.DGTD算法最大的一个优势是易于实现并行计算,作者在之前的论文中已实现GPU-DGTD算法,在此不再进行赘述(Feng et al.,2022).刘梅林和刘少斌(2008)将高阶Runge-Kutta DGTD方法应用于电磁场谐振腔的研究中.Xu等(2020)从数学角度研究了常系数双曲线性方程的RKDG方法,详细研究了能量方程的矩阵传递过程,给出了在标准CFL条件下保证L2范数稳定的充分条件.Xu和Zhang(2022)讨论了用基于偏迎风数值通量的DG方法求解一维变系数双曲方程,分别给出了其在半离散和全离散情况下的稳定性分析和hp误差估计.李林茜等(2016)从二维TM情形弱解方程出发,讨论了当前三角单元和相邻单元进行场量交互时数值通量的物理意义和不同形式.虽然众多学者在通量、时间离散方面进行了不同程度的研究,但对于探地雷达正演模拟,关于DGTD算法计算效率和精度的影响因素分析,仍有待进一步深入研究.

基于上述DGTD算法的研究现状和其他学者的研究基础,本文将DGTD算法应用到了探地雷达正演模拟中.从数值通量、时间离散格式、单元大小与基函数阶次、网格剖分方式4个方面,分析了它们对于DGTD算法的计算精度和效率的影响,并利用火星乌托邦平原模型证明了DGTD算法的有效性和实用性.

1 DGTD算法求解GPR波动方程

探地雷达在地下的传播符合电磁波理论,即Maxwell方程组.二维时间域TM波的标量方程为(Taflove and Brodwin,1975)

(1)

其中,ε、σ和μ为介质的物性参数,分别为介电常数、电导率和磁导率;t为电磁场的传播时间;Hx、Hy和Ez分别表示x、y、z方向上的电磁场分量;Jz为加载在z方向的电流源.

为了简化方便推导,将(1)式化简为(Lu et al.,2004)

(2)

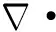
-∬Ωm(D(Um)φ)dΩm=-∮∂ΩmD(Um)φ·nmdl,(3)

如果不对局部解或者基函数加任何条件,那么对所有单元均成立的(3)式将会在单元边界上具有多解,因此,必须引入数值通量统一两个相邻单元的边界值,记为Um*.则(3)式变为

-∮∂ΩmD(Um*)φ·nmdl.

(4)

将(4)式的左边再做一次分部积分,可得到其强格式方程(Hesthaven and Warburton,2008)：

∮∂Ωm[D(Um)-D(Um*)]φ·nmdl,

(5)

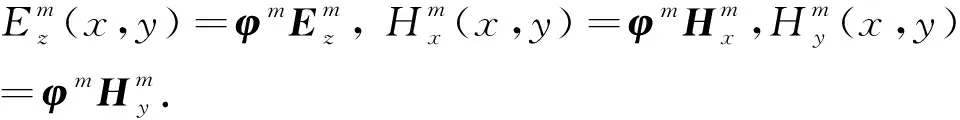
(6)

(7)

利用Runge-Kutta(RK)算法进行时间离散.为了方便理解和推导,进行如下变换：

(8)

采用s级显式RK格式进行离散,在时间步长Δt内可以表示为(Butcher,1976)

(9)

2 DGTD 算法影响因素

利用DGTD算法进行GPR正演时,影响其正演速度和精度的因素有很多.本文中作者选择了几个相对重要的因素展开分析与讨论,主要包括：数值通量、时间离散格式、单元大小与基函数阶次、网格剖分方式.

2.1 数值通量

数值通量具有很多种形式,为了GPR正演模拟的高精度,并且在计算过程中保持稳定性和收敛性,应当首先选择具有守恒性、单调性和相容性的数值通量.局部Lax-Friedrichs数值通量简单易懂,便于推导,是目前最快速、有效的方法之一.在第m个三角单元的边界上,二维TM模式下局部Lax-Friedrichs数值通量的表达式为

(10)

(11)

其中,εm为当前单元的介电常数;μm为当前单元的磁导率.

表1 DGTD中局部Lax-Friedrichs数值通量的三种形式Table 1 Three forms of local Lax-Friedrichs numerical fluxes in DGTD

2.2 时间离散

对显式的RK方案来说,级数s与阶数p的关系为p≤s.当p≤4时,p=s是可能存在的;而p≥5时,p级p阶的RK方案则不存在.这表明如若RK方案在5阶以上,则需要更多的中间变量和步骤来进行计算,这无疑会增大计算量,并且需要大型的储存空间.因此,本文为了在保证计算精度的同时,尽量提高计算速率,选择了4阶RK方案来进行时间上的离散,主要有以下三种(Hesthaven and Warburton,2008)：

(1)标准四级四阶显式RK方法(explicit RK,ERK)

(12)

其稳定性条件为

(13)

其中CN表示当前网格下,N阶DGTD算法的稳定性条件.

(2)五级四阶保持强稳定的显式RK方法(strong-stability-preserving RK,SSPRK)

(14)

其中,ai,bi,ci,di均为SSPRK系数(Hesthaven and Warburton, 2008).从上式中可以看出,此式需要储存5个中间变量,且比ERK多一个函数运算,其稳定性条件为

(15)

(3)低存储五级四阶显式RK方法(low-storage ERK,LSERK)

(16)

式中pi和ki为中间变量;αi,βi,γi为LSERK的系数(Hesthaven and Warburton,2008).其稳定性条件为

(17)

由(16)式可以看出,LSERK只需要储存两个中间变量即可.逐级进行求解时,只保存此级的p和k值,因此对内存的需求小.SSPRK和LSERK虽然都需要进行5级迭代,但允许更大的时间步长,这相当于抵消了多余的计算量.因此综合来看,LSERK这种方法比其他两种RK方法更具有优势.

2.3 单元大小与基函数阶次

在采用DGTD算法进行GPR正演模拟时,单元大小和基函数的阶次对正演模拟的计算效率和计算精度有着至关重要的影响.在直角等腰三角形I中,二维N阶基函数的定义为(Hesthaven and Warburton,2008)：

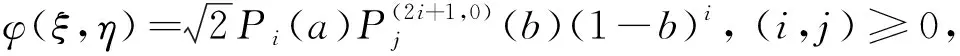
i+j≤N,

(18)

其中,

(19)

当基函数阶次较低或者网格数较少时,计算量小,计算效率高,但计算精度低.随着基函数阶次的提高或网格数的增大,将会提高计算精度,但也会增大计算量,降低计算效率.因此,需要对单元大小与基函数阶次进行影响因素分析,达到计算效率与计算精度之间的平衡.

2.4 网格剖分方式

在GPR正演模拟时,需要了解DGTD算法对不同网格的敏感程度,在网格剖分时避免因网格畸变所引起的计算精度降低.Delaunay剖分和前沿推进剖分都是GPR正演模拟中常用的网格剖分方式.所有三角形的外接圆均满足空圆性质的三角剖分,称为Delaunay三角剖分,即每个三角形的外接圆范围内(边界除外),不包含其他顶点(张岭和郝天珧,2006).而前沿推进法以相邻三点为基础,检验夹角的大小.如若为钝角,则在角的平分线上生成一个新的节点;如若为锐角,则将两条前沿的非公共点直接相邻,生成一个新的单元.前沿推进法生成的网格具有适应能力强,网格质量高等优势(马钧霆等,2015).因此,本文为了探究DGTD算法对于网格的依赖程度,选取了四种网格与常规用的非规则Delaunay三角剖分、前沿推进剖分进行对比.四种网格分别为：(a)等腰直角三角形;(b)等边三角形;(c)顶角为120°的等腰三角形;(d)顶角为30°的等腰三角形.其示意图如图1所示.

3 DGTD精度与效率分析

为了分析数值通量、时间离散格式、单元大小与基函数阶次、网格剖分方式对DGTD算法精度和效率的影响,选取了具有解析解的均匀模型来进行正演模拟,以便分析误差.此模型区域大小为1 m×1 m,其相对介电常数εr=4,电导率σ=6 mS·m-1,相对磁导率μr=1.激励源为主频900 MHz的雷克子波,在(0.5 m, 0.5 m)处激发(子图中的三角形)(图2).接收点位于(0.6 m, 0.6 m)(子图中的圆点).误差公式为

图1 不同网格形状示意图(a) 等腰直角三角形; (b) 等边三角形; (c) 顶角为120°的等腰三角形; (d) 顶角为30°的等腰三角形.

(20)

其中,utest为采用不同参数的DGTD算法正演模拟的结果;uref为二维均匀模型的解析解：

(21)

图2 二维均匀模型及其解析解灰色子图为模型示意图,三角形为激励源,圆形为接收点.

3.1 数值通量的影响

利用图2所示的二维均匀模型,分析迎风通量、中心通量和补偿通量对GPR正演模拟的影响.利用三角形对整个模拟区域进行剖分,基函数阶次N=3,时间采样间隔dt=1×10-11s,总模拟时间为10 ns.表2给出了不同数值通量的误差.为了更加直观地感受不同τ值的数值流量与解析解之间的误差,选择了几个典型流量做了A-Scan对比图,如图3所示.

从表2中可以看出,中心通量的误差是最大的,而在τ大于等于1/8后,误差基本在(3～6)×10-4之间,相差无几.这是因为在式(10)中,υ所乘的那一项称为耗散项.中心通量的υ=0,是没有耗散的,但是会出现伪解.在这个案例中,它的相对误差达到了31.7236,误差较大.补偿通量和迎风通量虽是耗散的,但是可以解决伪解的问题.因此,耗散项对于GPR正演模拟是非常有必要的.并且从表2中也可以看到,τ的值不能过小,否则相对误差会很大,给之后的GPR数据解译带来困难.同样的结论也可以由图3得到.当τ=1/50和τ=1/20时,波形与解析解存在很大的差异.而随着τ值的增大,波形与解析解基本一致,误差减小.在该模型中,τ=1/4时,误差最小.为了寻找到最优的τ值,对物性参数不同的模型采取了不同的基函数阶次和网格进行模拟,结果表明,τ的最优区间为[1/8,1].最优的τ值是根据模型变化的,不同的单元大小、基函数阶次也会改变其取值.为了避免出现伪解,又提高计算精度,推荐采用τ=1/2的补偿通量来进行高阶DGTD正演模拟.若想进一步提高精度,则需要对具体的模型案例做额外的分析实验.

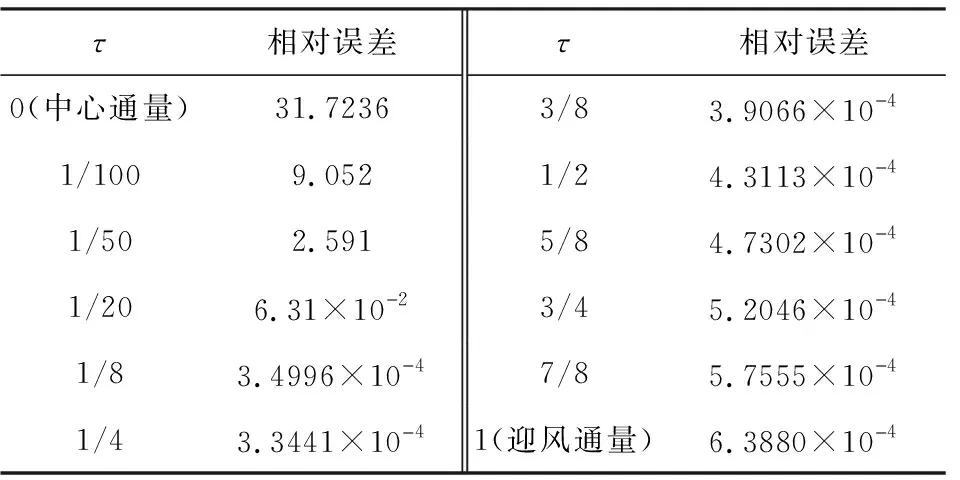
表2 不同数值通量的相对误差值Table 2 Relative errors of different numerical fluxes

图3 不同τ值的数值通量与解析解之间的A-Scan对比图

3.2 时间离散格式的影响

为了对比ERK、SSPRK和LSERK的优势,同样利用图2所示的二维均匀模型来进行正演模拟.因为ERK允许的时间步长较小,而SSPRK和LSERK允许的时间步长较大,因此先采用一个临界的时间步长值对比其稳定性条件.设置dt=3.9×10-11s,时间模拟总时长为10 ns,采用补偿通量τ=1/2来进行空间离散.三种离散方式下不同时刻的波场快照如图4所示.由图可见,在设置的时间步长条件下,2 ns时,三者的波场快照都是稳定的状态,并没有什么区别;而随着时间的推移,3 ns时,ERK已经开始出现色散的迹象,而基于SSPRK和LSERK时间离散格式的波场快照很光滑,不存在杂波;4 ns时,ERK的波场快照已经被污染,而SSPRK和LSERK还是很稳定的,并没有产生色散.因此可以看出,ERK的稳定性条件比SSPRK和LSERK的稳定性条件低,SSPRK和LSERK时间离散方案可以允许更大的时间步长.

图4 三种时间离散方案下不同时刻的波场快照(a), (b), (c) 分别为ERK、SSPRK和LSERK在2 ns时刻的波场快照;(d), (e), (f)为3 ns;(g), (h), (i)为4 ns.

此外,为了更加了解这三个时间离散方案的优势和劣势,在满足各自稳定性条件下,采用极限时间步长进行离散,对比其占用内存空间、正演模拟所需时间和精度,对比结果如表3所示.ERK为四级四阶,而SSPRK和LSERK为五级四阶,但当三种时间离散格式分别采取了不同的时间步长时,其正演模拟时间几乎相同.这是因为SSPRK和LSERK虽然每一个时间步会多一个函数计算,但是它们允许更大的时间步长,这相当于把额外的工作量抵消;在精度上,因为三种方法均为4阶精度,所以误差保持在同一水平,约等于4.31×10-4;在储存量上则有很大的差别,每一次启动时间离散方案时,ERK需要额外储存4个矩阵,SSPRK需要储存5个矩阵,而LSERK只需要额外储存2个矩阵.对于大型的复杂模型和三维正演模拟,LSERK有着巨大的内存优势,因此本文在接下来的影响因素分析中,将采取LSERK方案进行时间上的离散.

表3 不同离散时间格式的计算条件及特征Table 3 Characteristics and calculation conditions for different temporal integrations

3.3 单元大小与基函数阶次的影响

通过以上的实验可知,补偿通量τ=1/2和LSERK时间离散方案在GPR正演模拟中有较大的优势.除此之外,网格单元的大小与基函数的阶次对收敛速度也有很大的影响.同样利用图2所示的二维均匀模型进行正演模拟,采用不同的网格尺寸对模型进行空间离散,即网格数K分别为128、200、512、800、1250和2048;此外,在不同单元大小的情况下,分别采用基函数阶次N=1, 2, 3, 4, 5, 6来进行正演模拟,其相对误差值如表4所示.从中可以看出,网格数的增大和基函数阶次的提高均可以减小误差.而误差到达1.8×10-4时,不再向下减小,这是因为正演模拟的误差由空间离散和时间离散共同决定,此时已达到其时间离散的最高精度.因此当再减小网格尺寸和提高基函数阶次时,误差将不会减小.为了对其收敛性进一步分析,绘制了如图5所示的误差趋势图.图5a为单元数K对误差的影响,从中可以看出,基函数阶次相同的情况下,网格数越大,网格尺寸越小,其误差越小;此外,分析不同阶次下误差曲线的斜率可以看出,阶次越高,其误差收敛性越好.图5b为阶次N对误差的影响.同一网格下,阶次越高,误差越小;此外,网格数越多,其误差收敛性越高.分析两图可知,提高基函数阶次N或增大网格数K,均可以提高其误差的收敛性.

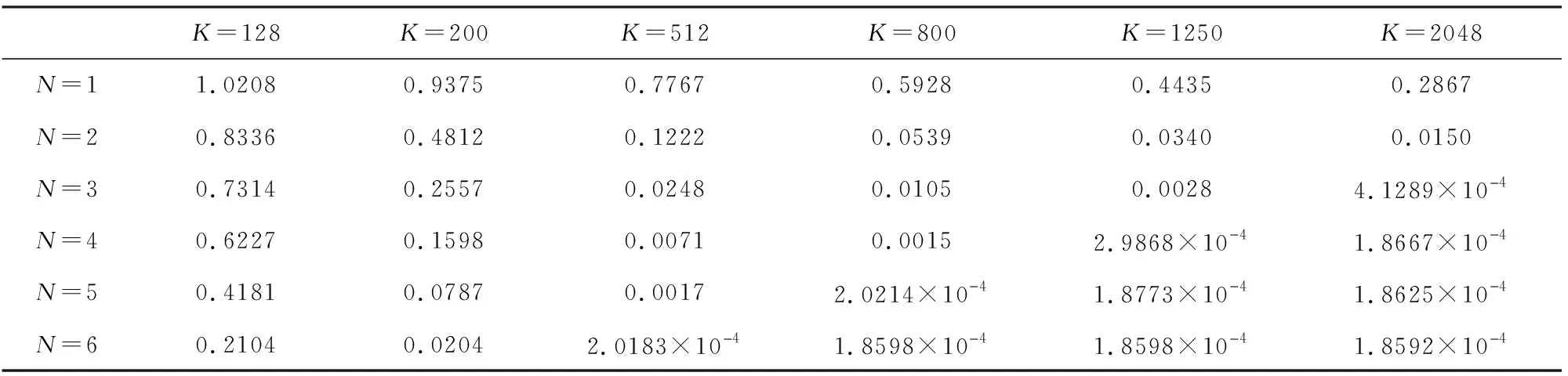
表4 不同单元大小与基函数阶次的相对误差值Table 4 Relative errors of different grid sizes and orders of basis function

图5 误差曲线趋势图(a) 误差随单元K的变化; (b) 误差随阶次N的变化.

从图5可以发现,阶次较小时,需要的网格数很多.而当阶次变大时,因时间离散的限制原因,增加网格数并不能提高计算精度,反而会增加计算量,降低计算效率.因此,需要在单元大小与基函数阶次之间寻找一个合适的关系,平衡计算效率与计算精度.电磁波波长λ计算公式为

(22)

其中,c为电磁波在介质中传播的速度;f为激励源的中心频率;c0为电磁波在真空中的传播速度,约为3.0×108m·s-1;εr为相对介电常数;μr为相对磁导率.由(22)式计算出,图2所示的二维均匀模型背景介质的电磁波波长为16.6 cm.图5a中红色虚线所示的误差为5×10-4.根据斜率计算出3,4,5,6阶在误差为0.5‰时所需要的网格数量,进而计算出单元大小.计算结果如表5所示.

从表中,可以得到d/N≈λ/15这个关系式.为测试此公式的普遍性,采用不同的基函数阶次、不同大小的网格进行正演模拟,计算其单元大小与误差,得到相同的结果.

表5 误差为0.5‰时,单元大小与基函数阶次之间的关系Table 5 The relationship between the grid size and the basis function order when the error is 0.5‰

3.4 网格剖分方式的影响

在GPR正演模拟中,为了避免因网格畸形引起的误差,需要了解不同的网格剖分方式对于计算精度的影响.因此,采用了如图1所示的4种网格来进行剖分,分别为等腰直角三角形、等边三角形、顶角为120°的等腰三角形及顶角为30°的等腰三角形,将它们与Delaunay剖分、前沿推进剖分方法进行对比.为了更加清楚地探究网格剖分方式的影响,只改变剖分三角形的形状,其他模拟条件保持一致.设置模拟区域的网格数K大致相等,约为500个网格.采用不同的基函数阶次N(1,2,3,4,5,6)进行正演模拟,所得到的误差值如图6所示.由图可见,随着基函数阶次的提升,四个网格的误差均在减小;而基函数阶次相同时,等边三角形的误差是最小的,其次是Delaunay剖分三角形和前沿推进剖分,而顶角为120°的等腰三角形误差最大.当基函数的阶次变大时,因网格剖分方式所引起的误差也在减小.总体上,它们都处于一个误差级别,相差不大.由此可得,高阶DGTD算法对于网格具有较好的适应性,网格剖分方式上的不足可以由更高阶次的基函数来补充.

图6 不同网格剖分方式的误差图

4 数值案例

中国首次火星探测任务“天问一号”配备了探地雷达系统,于2020年7月23日成功发射,于2021年5月15日成功着陆于火星乌托邦平原南部(Dong et al.,2022).选取最优的DGTD参数组合,应用到了火星乌托邦平原正演模拟中,表明所分析的DGTD算法对于复杂模型的适应性和准确性.根据乌托邦平原可能的地下结构(Li et al.,2022),建立图7a所示的模型进行数值模拟.整个模拟区域为120 m×60 m,相对磁导率为1,各层的介质和相对介电常数、电导率在表6中给出.编号②的地层中,有一些灰色的小岩块,为含冰玄武岩,用来模拟火山喷发时上涌的岩块,后又被沉积物所覆盖,并且离地面越近,岩块越小.采用DGTD算法进行正演模拟时,网格总数为16295,基函数阶次N=3,时间采样间隔dt=3×10-11s,总模拟时间为800 ns.采用主频为20 MHz的雷克子波作为激励源,激发点和接收点都设置在了地表处,如图7a中的红色三角形所示,总共接收195道数据.

图7b为DGTD算法模拟的地质雷达剖面.为了更好地解译地下介质,对该剖面做高度校正,让其更加贴合实际地形.由图7b可见,大约在170～200 ns、0～96 m处有一条反射波,那是①和②的地层分界面;400ns的位置也存在一条明显的反射波,那是②的下界面,经过高度校正后的反射波波形准确地反映了含冰风成沉积物的起伏.在0～60 m的水平位置,该反射波的幅值较小,而60～120 m处,地层分界面较明显.这是由于③磁铁矿的相对介电常数与②差异较小,因此反射波较弱.图7b中红色椭圆形A所圈出的位置,为上涌到②号地层(含冰风成沉积物)处的小含冰玄武岩块的双曲线反射波;虚线矩形B所表示的位置为③号地层的下界面;实线矩形C处为④与⑤的地层分界面.这些反射波都与图7a的模型相对应.这说明了最优参数组合的DGTD算法在探地雷达正演模拟中的准确性,可指导火星实测数据的解译.

图7 复杂模型示意图及其剖面图(a) 火星乌托邦平原二维模型示意图; (b) 剖面图.

5 结论

(1) 作者将DGTD算法引入到GPR正演模拟中,推导了DGTD算法的弱解形式,介绍了三种数值通量和时间离散方案.从数值通量、时间离散格式、单元大小与基函数阶次、网格剖分方式4个方面,分析了DGTD算法的计算精度和效率.

(2) 数值模拟实验表明,Lax-Friedrichs数值通量中τ=1/2时的补偿通量,既可以消除伪解,又可以提高计算精度;低存储显式Runge-Kutta方案在GPR模拟中更具有优势.而提高基函数的阶次或增大网格数,均可以提高算法精度;误差为0.5‰时,网格与阶次的一个适用关系为d/N≈λ/15.不同的网格剖分方式表明,网格的形状对于高阶DGTD算法的影响较小,也证明DGTD算法对于网格的适应性强.

(3) 本文中作者采用DGTD算法仅开展了二维TM模式下的GPR正演.下一步的研究方向为将DGTD算法应用到大尺度三维GPR正演模拟中,并实现hp型自适应,拓宽DGTD算法的适用性,为GPR反演奠定理论基础.