多采样率地震勘探技术(MrSET)探讨

倪宇东, 姜福豪, 邹雪峰, 蓝益军, 柳兴刚, 门哲, 许银坡

中国石油东方地球物理公司, 涿州 072751

0 引言

时间采样以及空间采样问题是地震勘探基本问题,采样方式包括规则采样、非均匀(非规则)采样、随机采样等.关于信号采样方式与数据重建等问题,Niquist于1928年给出采样定理(Nyquist,2002; Shannon, 1949),广泛应用于通讯、医学、地球物理等领域;1953年Black提出了非均匀采样的思想(Black,1953; Dippé and Wold, 1992; Duijndam and Schonewille, 1999);Yen(1956)进一步给出了关于特殊类型非均匀采样的4个定理,同时讨论了数据重建问题.1957年前后出现多采样率采样模拟电路系统(Kranc, 1957),1967年发表的论文论述了时间域、频率域多采样率采样数据等效性(Brogan, 1967; Jury, 1967),1978年一种多采样率方法尝试应用到地震数据处理领域(Lu and Gupta, 1978).截止到今天,多采样率信号处理依然是电子技术与信息科学重要技术领域之一(Göckler and Groth, 2004).信号重构的数学理论日趋完善,相关算法已取得了显著进步(Candès and Romberg, 2006; Candès et al., 2006;Proakis and Manolakis, 2006; 李衍达和常迵,1991). Donoho(2006)详细论证了压缩感知基本原理,随即得到了广泛的关注(Lustig et al., 2008).随机采样是该理论重要基础之一(Leneman, 1966). Elder和Kutyniok(2012)指出,随机采样构建的感知矩阵,特别是感知矩阵的元素选为与高斯、伯努利或更一般的任何子高斯分布有关的,都将高概率满足约束等距(Restrained Isometric Property,RIP)条件,也就是能够高概率、高保真恢复输入信号.

自压缩感知理论建立以后,基于压缩感知的随机采样在地震勘探实践中尝试应用.李成博和张宇(2018)提出了基于压缩感知的地震数据成像技术(Compressive Seismic Imaging,CSI),Mosher等(2012,2014)介绍了该技术：包括非均匀(非规则)最优化采样(Non-uniform Optimal sampling,NUOS)、地震信号稀疏化处理、数据重建、时间同步源数据分离等技术(唐钢和杨慧珠, 2010; Mosher et al.,2012).随机采样、非规则采样在地震勘探领域早已有之(Schuster and Zhou, 1996; Hennenfent and Herrmann,2008; Herrmann, 2010; Vermeer, 2010),Cordsen等(2000)强调物理点位随机设计的优势是改善炮检距与方位角的分布与静校正耦合,同时还考虑了土地使用许可问题.Hardage等(2011)指出,合理数量的物理点随机分布时,P-P、SH-SH或 SV-SV数据的炮检距分布更加均匀,有利于分析振幅随炮检距变化和属性随方位角变化规律的研究.

地震勘探领域关于不同空间采样方式定义较多且容易混淆,包括“均匀采样、非均匀采样、多采样率、规则采样、非规则采样、随机采样”等(Nyquist,2002;Black,1953;Yen, 1956;Vermeer, 2010),尚未形成不同空间采样技术系统的理论.作者将从地震波场的带限性与空间域非均匀性出发,定义了多采样率地震勘探技术(MrSET),组合了不同空间采样方式.该技术在继承规则采样观测系统面元属性特征的同时,进一步优化面元属性特征,提高成像精度.作者提出多采样率地震勘探采集观测系统设计5项准则,介绍数据处理基本方法及效果.与规则采样相比,在相同成本、相同道密度情况下,多采样率地震勘探技术能够更好解决复杂地震波场、弱能量地震信号充分采样以及高精度成像问题,经过进一步研究将是(陆上、海洋等)节点地震勘探时代常规技术.

1 地震波场是时空不均匀带限信号

地震波在频率域具有带限性,地震波是时间(t)、频率(f)的函数,频带宽度是有限的,是带限信号(David et al., 2021).对于地震勘探而言,震源是带限的,大地是低通滤波器,接收系统是带通滤波器,地震子波在传播过程中经过大地的吸收衰减、球面扩散、地层反射等形成的地震波场,存储到地震勘探仪器系统中,这个过程决定了地震波具有频率域带限性.地震勘探能够记录到的地震波最高频率一般都低于250 Hz,小折射、微测井等表层结构调查方法可能记录更高频率地震波,但是根据Niquist采样定理,工业界完全可以采用2 ms、1 ms、0.5 ms甚至更小的采样周期实现地震波充分采样,达到有效保护宽频信息、高频信息,保护更好的时间分辨率.地震波时间域充分采样增加的成本同地震勘探项目投资相比完全可以忽略不计.地震勘探数据采集项目在采集方法设计阶段就规定了采样周期,在野外数据采集过程中采样周期一般是不变的常数.

地震波场空间域具有不均匀性,地震波场是时间(t)、频率(f)的函数,也是空间(x,y,z)、波数(k)的函数,波场复杂程度与沉积特征、构造变形特征等密切相关.多期构造运动与沉积旋回、风化剥蚀与溶蚀等地质作用,使断裂系统发育特征、地层倾角变化、地层岩石物性及厚度横向变化、风化剥蚀面形态、沉积间断边界展布特征等非常复杂,折射波、反射波、绕射波、散射波、多次波等相互交织,空间域地震波场非常复杂,具有不均匀性,导致在空间域对记录波场的解释具有不确定性.目前工业化应用的规则采样观测系统较难实现对复杂波场的完全、精确、充分采样.受有线仪器数字传输电缆上固定道间距以及安全、环保政策、投资成本等限制,地震勘探采集项目仍然以空间规则采样为主,物理点空间采样间隔是空间常量,采集方法主要考虑反射波成像不产生空间假频,这种方式难以对复杂波场,特别是绕射波、散射波等弱能量地震信号充分采样.采用多采样率地震勘探技术(MrSET)能够最大限度实现对复杂波场的充分采样,特别是对绕射波、散射波等弱能量信号的充分采样.地震勘探中的空间规则采样、随机采样、非均匀采样、非规则采样等不同的采样方式,可以统一到多采样率技术框架.

假设连续地震波场为wo(t,d),离散地震波场为w[m,n].其中：t代表时间、d代表空间,m,n为正整数,表示离散的时间和空间采样点序列.第[m,n]个离散信号数值等于连续地震波场在tm,xn处的值,表示为

(1)

式中Δtm+1,m为第m与第m+1个离散时间采样点之间的采样周期;Δxn+1,n为第n与第n+1个离散空间采样点之间的间隔或代表观测系统中的道距、炮点距等参数;Δtm+1,m、Δxn+1,n的倒数即为采样率,分别是频率fm+1,m、波数kn+1,n.本文研究的时间域采样周期只有一个,因此M=1;如果空间采样间隔只有一个,则N=1;如果有多个不同取值的空间采样间隔,或有多个不同取值的空间采样率,则N>1.

地震勘探采集观测系统中,道距、炮点距、接收线距、炮线距具有一个及一个以上不同取值的采样方式统称为多采样率采样,采用多采样率采样的地震勘探技术称为多采样率地震勘探技术(Multirate Seismic Exploration Technique,简称MrSET).MrSET的命名主要考虑三个方面：一是体现了地震勘探数字信号、离散信号处理的特征;二是避免了随机采样、非均匀采样、非规则采样与野外观测系统变观后物理点分布特征相互混淆的问题.当然,由于地表存在障碍物,野外观测系统变观通常会使炮点、检波点分布不均匀,这种情况不是严谨的多采样率采样;三是考虑炮点、检波点等物理点测量精度与野外施工点位误差问题.MrSET重要理论基础是“观测系统物理点空间采样间隔在空间上是变量,可以拓宽空间波数k,最大概率逼近复杂地震波场而实现充分采样,特别是最大概率实现对绕射波、散射波等弱能量地震信号的充分采样”.

多采样率数据采集观测系统道距、炮点距、接收线距、炮线距在空间上是变量.假设多采样率观测系统中有N个取值的道距Δxi或炮点距Δyj,这里N≥1、1≤i,j≤N,N、i、j是正整数.当N=1时,多采样率采集是传统的规则采样,否则就是随机采样或非均匀采样、非规则采样.为使问题简化,这里举例说明：当N=1时,i、j=1,Δxi或Δyj仅有一个取值,如Δx1=20 m、Δy1=40 m,inline与crossline方向的空间波数(空间采样率,×102)分别是kx=5.00、ky=2.50,Nyquist空间波数(Nyquist空间采样率,×102)分别是kxNyq=2.50、kyNyq=1.25,这是传统的规则采样,inline与crossline方向各有一个采样周期(采样间隔)、一个采样率.假设N=5,i、j=1、2、3、4、5,Δxi或Δyj分别有5个取值(单位：m),如Δxi={20,21,23,25,27}、Δyj={40,42,43,45,50};inline与crossline方向的空间波数(空间采样率,×102)分别有5个取值：kxi={5.00, 4.76, 4.35, 4.00, 3.70}、kyj={2.50, 2.38, 2.33, 2.22, 2.00},Nyquist空间波数(Nyquist空间采样率,×102)分别有5个取值：kxiNyq={2.50, 2.38, 2.18, 2.00, 1.85}、kyjNyq={1.25, 1.19, 1.17, 1.11, 1.00},这就是多采样率采样,两个方向分别有5种取值的采样间隔与采样率,利用不同的准则确定不同取值的采样间隔或采样率,就可以得到随机采样、非均匀采样或非规则采样.

2 多采样率地震勘探采集参数设计

多采样率采样采集参数设计同样要考虑满足叠前偏移成像需求.基于叠前偏移Kirchhoff积分方法原理,假设地下目的层的任意一成像点r=r(x,y,z),介质分布均匀,速度为c,深度为z,其远场三维叠前Kirchhoff偏移公式(麻三怀等,2008)为

(2)

式中m(r,ω)为成像点r的偏移成像,Γs和Γg分别为炮、检点阵列的面积;f(rs,rg)表示炮点和检波点分布的(x,y,z,f)四维采样函数;rij=|ri-rj|,其中：

f(rs,rg)=f(sxy,sz,sf;gxy,gz,gf),

(3)

(4)

基于公式(4),通过评价全区成像点的成像效果(丁建荣等, 2022),实现多采样率采样点优化设计.

无线节点仪器的使用不仅使传统有线仪器时代观测系统参数设计发生了巨大变化,也为多采样率采样提供了应用条件.使用无线节点仪器,道距大小可以灵活变化,不再受数传电缆上固定长度道距的限制,这样就使面元可以在道距、炮点距两个空间方向上灵活变化,为多采样率地震勘探技术的应用提供了基础.

多采样率地震勘探采集观测系统设计建议考虑以下5项准则：

(1)道密度一致准则：道密度是决定成像精度最重要的参数之一,特别是低信噪比地区,野外采集数据达不到一定数量的道密度,是无法满足高精度成像处理要求的.考虑反射波偏移成像精度,按照反射波“充分采样”的原则确定传统规则采样观测系统道密度TDr,TDr作为多采样率基本道密度,在此基础上优化观测系统,获得多采样率采样观测系统.

(2)“整体均匀、局部随机”准则：多采样率采样不是任意随机采样,多采样率采样观测系统要求炮点、检波点分布“整体均匀、局部随机”.首先根据地质任务要求以及资料信噪比情况,按照“均匀采样、对称采样”的原则,分析论证传统规则采样观测系统道距Δx、炮点距Δy等参数,在接收线与炮线上按照Δx、Δy等间隔剖分网格,在每一个网格内部,采用jitter采样(张华和陈小宏, 2013)、并采用感知矩阵列间相关性评价指标μ值公式(5)(周松等, 2017)约束jitter采样等方法优化炮点、检波点位置(Ni et al., 2021),从而实现“整体均匀、局部随机”准则.公式(5)为

(5)

式中ψ为感知矩阵,与采样点位置有关,μ为感知矩阵列间最大的相干系数,其地球物理含义是非规则采样造成的傅里叶正交性被破坏引起的最大频谱泄露.

(3)绕射波、散射波成像准则：在复杂断裂系统、中小尺度多层叠置砂体、碳酸盐岩断溶体与丘滩体等发育的勘探区域,在基岩与碳酸盐岩风化壳及其内幕非均质储层发育的勘探区域,要根据地震、地质等资料,建立地震地质模型,通过数值正演模拟获得上述地质目标的绕射波、散射波波场分布特征,分析绕射波、散射波成像时要求不产生空间假频的最小道距Δxmin、最小炮点距Δymin等面元参数.多采样率观测系统中一般要包含一定数量的Δxmin、Δymin样本,从而在投资成本可控的前提下,最大概率逼近对绕射波、散射波等弱能量地震信号的充分采样.

(4)道距、炮点距取值范围选择准则：多采样率采样观测系统面元大小是空间变量,变量取值范围取决于道距Δxi、炮点距Δyj变化范围.在充分考虑Δxmin、Δymin以及逆散射成像处理技术的前提下,建议在低信噪比区,道距、炮点距取值范围采用公式(6)：

(6)

其他地区采用公式(7)：

(7)

(5)真倾角方向准则：对于长轴背斜、地质体具有明显走向与倾向的勘探项目,建议在真倾角方向或垂直构造走向方向上采用多采样率采样.考虑到炮点位置受地表条件限制较多,因此建议接收排列垂直构造走向,道距采用多采样率.

多采样率采样观测系统设计继承了传统规则采样观测系统“充分采样、均匀采样、对称采样”的原则,同时对传统规则采样观测系统进一步优化,观测系统方位角、炮检距等分布,特别是中小炮检距分布更加均匀、连续.

3 多采样率地震勘探数据处理方法

多采样率数据处理应考虑散射波成像处理与数据重构,这是与规则采样数据处理最大的不同;当然,多采样率数据处理也应该考虑多尺度数据正演与反演、多尺度偏移速度场建模、分频多尺度去噪以及多尺度近地表结构建模等,从而发挥多采样率采样数据优势.

多采样率地震勘探数据包含更丰富的绕射波、散射波信息,使用逆散射偏移成像处理技术处理多采样率地震数据能够发挥多采样率地震勘探技术优势.目前大多数偏移反演方法都是基于线性单散射近似,也就是一阶Born近似(Ouyang et al., 2015).散射场一阶Born近似更符合反射波勘探的一次波假设,单散射近似与偏移之间存在理想的线性关系,满足产生散射的地质体尺度较小以及速度、密度等物性参数扰动不大等弱散射条件.基于一阶Born近似的偏移反演方法适用于单砂体、不整合面或尖灭线、断层断点等的偏移成像处理(范白涛等, 2022).油气勘探地质目标往往是断溶体、丘滩体、基岩与碳酸盐岩风化壳及内幕非均质岩性油气藏等,基于散射场二阶Born近似的反演成像方法有利于这类地质目标的保幅成像处理,这类地质目标弹性参数和密度等纵横向不均匀变化引起较强扰动散射波场,多次散射中二次散射对散射场能量贡献不能忽略.目前逆散射偏移成像方法没有得到广泛应用.如果地震资料信噪比较低,可以直接利用基于反射波的积分法叠前偏移技术处理多采样率地震数据,与相同道密度传统规则采样数据体的成像精度相比,可以进一步提高成像精度,特别是中浅层成像分辨率、高陡地层以及断层断面成像精度、风化壳成像精度等等都有所提高.

如果信噪比较高,可以利用基于Radon变换(Shao and Wang, 2022)、地震波干涉方法(Wang et al., 2009,2010)等插值方法提高道密度,本文采用基于压缩感知的数据重构技术.数据重构可以是非规则重构、也可以是规则重构,无论采用何种数据重构技术(赵虎等, 2023),处理后的数据体应最大限度保留多采样率采样数据特征,要保留小道距、小炮点距数据,否则会丢失大量真实位置的地震波场信息,取而代之的是大量通过数学运算产生的非真实位置的地震道信息,从而违背多采样率地震勘探技术基本理论.假设wr是野外采集到的地震波场,φ为测量矩阵(或叫采样矩阵,与观测系统有关),wf是期望通过数据重构获得的更高密度地震波场,wf也是真实地震波场的近似.不考虑噪声情况下,重构wf的过程就是解式(8)的过程：

wr=φwf=ψs,

(8)

(9)

4 数值模拟与试验数据分析

三维数值模拟使用SEG盐丘模型(图1).模型长13500 m、宽13500 m、深4000 m,数值模拟使用主频为8 Hz雷克子波作为激发源,记录长度6 s,时间采样间隔2 ms.首先使用传统规则采样三维观测系统GS1完成声波数值模拟并获得高密度规则采样正演数据：道距ΔR=40 m,炮点距ΔS=40 m,接收线距ΔRL=80 m,炮线距ΔSL=200 m.在Gs1正演数据基础上抽稀形成规则采样数据体,观测系统设为Gs2：道距ΔR=160 m,炮点距ΔS=160 m,接收线距ΔRL=160 m,炮线距ΔSL=200 m,共4575炮,道密度约6.25万道/km2.在Gs1正演数据基础上抽稀形成多采样率数据,观测系统设为Gs3：道距ΔR采用固定值,ΔR=160 m;炮点距ΔS采用多采样率,用μ值约束jitter采样抽稀数据,40 m≤ΔS≤280 m,炮点距变化步长为40 m,ΔS共有8种取值(ΔS=40、80、120、…、240、280 m)、8种取值采样率,4575炮,平均道密度约6.25万道/km2.利用阈值类算法对Gs3数据体非规则数据重构,形成观测系统Gs4数据体,Gs4观测系统为：道距ΔR采用固定值,ΔR=160 m;炮点距ΔS采用多采样率,用μ值约束jitter加密采样,40 m≤ΔS≤200 m,炮点距变化步长为40 m,ΔS共有5种取值(ΔS=40、80、120、160、200 m)、5种取值采样率,6081炮,在Gs3基础上增加了1506炮.图2a、b、c、d、e、f分别是Gs2、Gs3、Gs4对应的PSDM剖面及三维立体PSDM图.从剖面上看,Gs2对应的PSDM剖面在盐丘陡倾角边界或断层形成的偏移噪声能量强、截断了水平地层反射,盐丘以下深层噪声较大;相同道密度情况下,Gs3对应的PSDM剖面盐上偏移噪声偏弱,盐下信噪比提高,Gs4对应的PSDM剖面盐上偏移噪声最弱,盐下信噪最高;从立体成像图可以看到Gs2整体偏移噪声最强、Gs3偏移噪声变弱、Gs4偏移噪声最弱.PSDM剖面以及成像立体图对比结果说明,在相同道密度情况下,多采样率数据成像偏移噪声弱于规则采样,成像信噪比、成像精度高于规则采样;在高信噪比情况下,数据重构能够进一步提高多采样率数据成像精度、提高成像信噪比.

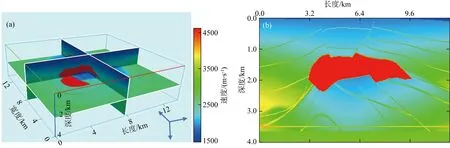
图1 三维数值模拟SEG盐丘速度模型及切片(a) 速度模型; (b) 典型速度切片.

图2 PSTM剖面及立体切片(a)、(b)、(c)分别是规则采样观测系统Gs2、多采样率观测系统Gs3以及多采样率观测系统非规则重构后Gs4对应的PSDM剖面; (d)、(e)、(f) 分别是Gs2、Gs3、Gs4对应的PSDM成像立体图.

2021年完成中国西部某盆地多采样率地震勘探技术试验,传统规则采样观测系统采用正交观测系统,观测系统用Gy1表示,道距ΔR=40 m,炮点距ΔS=40 m,面元为20 m×20 m,接收线距ΔRL=160 m,炮线距ΔSL=160 m,726次覆盖,道密度约181.5万道/km2.多采样率观测系统用Gy2表示,用μ值约束jitter采样布设检波点位置.道距取值范围：10 m≤ΔR≤70 m,道距变化步长为1 m,ΔR共有61种取值(ΔR=10、11、12、…、68、69、70 m)、61种取值采样率;炮点距ΔS=40 m;最小面元为5 m×20 m,最大面元为35 m×20 m;接收线距ΔRL=160 m,炮线距ΔSL=160 m,平均覆盖次数726,平均道密度约181.5万道/km2.

图3是Gy1、Gy2检波点分布图(局部),蓝色点是Gy1检波点,道距ΔR=40 m;红色星号是Gy2检波点,道距是变化的,ΔR=10、11、12、…、68、69、70 m.图4是传统规则采样观测系统Gy1、多采样率观测系统Gy2不同道距与不同取值道距个数统计图,红色矩形点框对应Gy1,说明Gy1道距是常量;蓝色棒状图对应Gy2,可以看出不同取值道距个数呈现正态分布.

图3 规则采样观测系统Gy1、多采样率采样观测系统Gy2检波点分布图Gy1检波点是蓝色点,道距ΔR=40 m;Gy2检波点是红色星号,道距是变化的,ΔR=10、11、12、…、68、69、70 m.

图4 规则采样观测系统Gy1(红色矩形点框)、多采样率采样观测系统Gy2(蓝色棒状图)道距(点距)与不同取值道距(点距)个数统计图

图5a、b分别是Gy1、Gy2对应的炮检距-道数分布统计图,由于是高密度、宽方位观测系统,两者炮检距-道数分布总体趋势相同,但是规则采样Gy1炮检距-道数分布具有台阶状特征,而多采样率采样Gy2炮检距-道数分布具有渐变、连续的特征,更有利于复杂波场、特别是绕射波、散射波的连续、充分采样.图6a、b分别是Gy1、Gy2对应的方位角-中点个数分布统计图,同样由于采用高密度、宽方位观测系统,两者方位角-中点个数分布总体趋势相同,规则采样Gy1方位角-中点个数分布出现毛刺状特征,不利于复杂波场连续、充分采样,而多采样率采样Gy2方位角-中点个数分布具有连续的特征,利于复杂波场连续、充分采样.图7a、b分别是Gy1、Gy2对应的方位角-炮检距-道数玫瑰图(局部),相邻同心圆径向距离30 m、切向按照每隔5°剖分.图中不同颜色代表不同取值炮检距的道数,白色方块表示缺失地震道.由图可见,规则采样Gy1在0°～360°之间大量缺失炮检距小于1000 m的地震道,而多采样率采样Gy2在inline方向上缺失炮检距小于400 m的地震道;在crossline方向上,缺失炮检距小于1000 m的地震道(与炮点距不变有关).显然,与多采样率采样Gy2相比,规则采样Gy1缺失中小炮检距地震道的情况更加严重,多采样率采样更加有利于中浅层、陡倾角断面及地层等的反射波或绕射波、散射波充分采样与高精度成像.

图5、图6、图7对比结果充分说明,在相同道密度情况下,多采样率采样观测系统炮检距、方位角分布在继承规则采样对地震波场连续、均匀、对称采样的同时,更有利于复杂地震波场、绕射波等弱能量地震信号的无假频充分采样.

图8a、b分别是规则采样、多采样率采样单炮记录,两张记录没有明显区别,背景噪声都比较强、有效反射时隐时现,多采样率采样没有明显优势.图9a、b分别规则采样、多采样率采样数据的速度谱及道集,道集位于构造倾角较大的位置(图10红色倒三角位置).与规则采样相比,多采样率数据速度谱能量聚焦好、道集信噪比高.图10a、c是规则采样PSTM剖面,图10b、d是多采样率采样PSTM剖面,分别对比(a)与(b),(c)与(d),多采样率采样PSTM剖面信噪比高于规则采样PSTM剖面,主要原因是规则采样数据高频信息出现空间假频,在资料处理时出现偏移噪声污染了PSTM剖面;对于中浅层成像精度、高陡地层以及断面成像精度、断点绕射收敛情况,多采样率采样PSTM剖面成像精度高于规则采样PSTM剖面,主要原因是多采样率采样对于弱能量绕射波能够充分采样,偏移处理时有利于能量聚焦收敛.剖面(c)、(d)位于工区边缘,资料覆盖次数较低,多采样率采样成像精度优势更加明显.图11a、b分别是规则采样、多采样率采样PSTM时间切片,对比结论与图10相同.

图5 炮检距-道数分布统计图(a) 规则采样观测系统Gy1炮检距-道数分布统计图; (b) 多采样率采样观测系统Gy2炮检距-道数分布统计图.

图6 方位角-中点个数分布统计图(a) 规则采样观测系统Gy1方位角-中点个数分布统计图; (b) 多采样率采样观测系统Gy2方位角-中点个数分布统计图.

图7 方位角-炮检距-道数分布统计图(a) 规则采样观测系统Gy1方位角-炮检距-道数分布统计图; (b) 多采样率采样观测系统Gy2方位角-炮检距-道数分布统计图.不同颜色代表不同道数.

图8 不同采样方式单炮记录(a) 规则采样Gy1单炮记录; (b) 多采样率采样Gy2单炮记录.

图9 速度谱及道集记录(a) 规则采样Gy1速度谱及道集记录; (b) 多采样率采样Gy2速度谱及道集记录.

图10 不同采样方式PSTM剖面(a)、(c) 规则采样Gy1的两条PSTM剖面; (b)、(d) 多采样率采样Gy2的两条PSTM剖面.其中(a)与(b)位置相同,(c)与(d)位置相同且不满覆盖.

图11 不同采样方式时间切片(a) 规则采样Gy1时间切片; (b) 多采样率采样Gy2时间切片.

5 技术优势

多采样率地震勘探技术(MrSET)主要有7个方面技术优势：

(1)大概率逼近对复杂波场、弱能量绕射波、散射波等的充分采样,为高精度成像提供数据基础.

(2)小取值空间采样间隔(大取值采样率)的存在,拓宽了Nyquist空间波数,使折叠频率提高、进一步保护了相对高频信号,拓展了有效频带宽度,有利于提高成像精度、有利于提高横向分辨率.

(3)有利于压制高频偏移噪声,特别有利于提高陡倾角地层、断面等成像精度.

(4)非规则采样能够更多捕捉到特殊地质体绕射波、散射波等信息,有利于特殊地质体高精度成像处理,如断溶体、砂体、不整合等等高精度成像处理.

(5)多采样率对应多个折叠频率,减弱了规则采样折叠频率能量强、污染大的现象.多个折叠频率相互干扰、能量减弱甚至呈现随机噪声特征,有利于信噪分离处理.

(6)不同取值空间采样间隔的存在,满足了中浅层、深层多层系立体勘探的要求.

(7)有利于提高近地表结构反演精度,有利于偏移速度场建模.

6 结语

多采样率采样组合了传统规则采样以及随机采样、非均匀采样、非规则采样等采样方式;多采样率地震勘探技术在遵循“整体均匀、局部随机”设计原则基础上,继承了传统规则采样“充分、均匀、对称”采样优势.多采样率地震勘探技术是高精度、高保真地震勘探技术,将有巨大潜力成为(陆上、海洋)节点地震勘探时代常规技术.

致谢感谢审稿人对完善本文提出的宝贵的具有建设性的意见和建议,感谢东方地球物理公司采集技术中心闫智慧、何宝庆、侯喜长、雷云山、张纯、韩明怡、盛洁、杨晓玲、皮红梅等同事提供的帮助.